多目标模糊机会约束规划的低碳多式联运路径优化

张 敏，韩晓龙

（上海海事大学 物流科学与工程研究院，上海 201306）

0 引言

全球经济的迅猛发展和国际贸易往来深化快速带动了多式联运的发展和完善，但同时也导致环境污染和能源紧缺问题日益严重，由温室气体排放引起的全球气候变暖已经成为全社会共同面对的严峻问题。在全球碳排放统计中，交通运输占比高达14%，而道路碳排放占整个运输部门碳排放量的70%［1］。在此形势下，多国以保护环境为目的，提出要对二氧化碳排放征收碳税。基于此，本文运用碳税值计算碳排放成本，对多式联运网络的运输方案进行探究，并分析碳税值变化对运输方案的影响。

近年来，多式联运中的低碳话题层出不穷。Figliozzi等［2］指出尽管商用车辆的使用和影响不断增加，但很少有研究将减少排放作为路线问题的主要目标；Caris 等［3］认为除了终端网络设计、多式联运服务网络设计、多式联运路径等方面的考虑，还应将环境问题加入多式联运决策建模中。因此，碳排放是在模型中必不可少的因素之一。张旭等［4］针对不同碳排放政策下模糊需求的路径优化问题，建立基于区间的鲁棒优化模型，结果表明碳税的减排力度比碳交易、强制碳排放政策更强；Fahimnia 等［5］提出了一种策略性的供应链规划模型，该模型在碳税政策计划下整合了经济和碳排放目标；蒋琦玮等［6］探究了运输时间不确定的集装箱多式联运路径优化问题，表明碳税值逐渐增大可以有效促进多式联运货运人选择更为低碳的运输方案，对经济和环境都能产生有利的结果。但考虑碳排放的车辆路径问题的研究起步较晚，大多数研究仅局限在对确定环境下的车辆路径问题中。Liao等［7］将仅卡车运输的二氧化碳排放量与多式联运沿海运输进行比较，结果表明，用联运代替长途卡车运输可以显著减少二氧化碳排放；Pizzol［8］进一步验证了多式联运比单一运输方式更节能减排；蒋玲茜等［9］分析碳排放影响因素并建立海陆多式联运碳排放计算模型，得出“铁-海-铁联运”模式为最优方案。以上研究表明，碳税值的提出与多式联运的发展对减少碳排放都有显著的成效。

随着社会节奏的日益加快，各大行业的作业效率在不断提高，消费者们提出了更为个性化、精细化的服务需求。多式联运的相关研究也从确定性问题逐渐转向不确定性问题，Cheng 等［10］最早提出了带有模糊预约时间的车辆路径问题，并研究了单对单货物收发情况下的车辆路径问题；李晶等［11］对医药物流多模糊时间窗的车辆路径问题（Vehicle Routing Problem，VRP）进行建模，引入多模糊时间窗来评价客户的满意度；Goncalves 等［12］基于可信性理论，通过建立模糊机会补偿模型，用模糊模拟和智能算法来求解带时间窗的路径优化问题；彭勇等［13］通过蒙特卡洛方法处理多式联运网络中的不确定性，设计基于非支配排序的多目标蚁群算法求解；除此之外，耿娜娜等［14］以不确定条件下的中欧班列多式联运路径优化为研究对象，建立双目标优化模型，求解并验证了模型的有效性；Shi 等［15］考虑了具有模糊需求的家庭医疗药物的调度问题，构建模糊机会约束模型，提出了一种混合遗传算法与随机模拟方法相结合的求解方法；谢静等［16］引入三角模糊数解决需求模糊情形下多式联运路径选择问题，利用逐步法求解模型，但三角模糊数缺乏灵活性；Sun等［17］使用梯形模糊数表示模糊需求，将多个运输订单作为优化对象，建立了模糊混合整数非线性规划模型，采用线性化技术来重新构造清晰模型，最终通过标准数学编程软件解决。

目前，通常使用随机规划与模糊规划来表述不确定性参数，但大多数情况下，没有足够的数据供决策者拟合需求的概率分布，因此随机规划的可行性较低。同时，现有研究中常用三角模糊数表示模糊需求量，运用梯形模糊数表示模糊时间窗，运用梯形模糊数表示模糊需求量的研究极少，但三角模糊数隶属度的最大值只能对应一个点，仅适用于定义明确的范围，相比之下梯形模糊数则更为灵活，其隶属度的最大值可对应一个区间，允许不同的决策者对最可能值持有不同的意见，有学者提出运用梯形模糊数表示模糊需求量能够更好地匹配实际情况。因此，本文使用更为灵活的梯形模糊数表示模糊需求量与模糊时间窗，引入碳税值计算碳排放成本，对具有多模糊参数的多式联运问题进行研究，并分析碳税值与模糊需求量偏好值的变化对优化结果的影响。

1 问题描述与模型建立

1.1 问题描述

如图1 所示，由若干个节点所构成的运输网络中，节点之间可双向或单向连通，不连通的节点之间运输距离用超大数值表示。任意两节点间最多存在公路、水运和铁路三种运输方式。不同运输方式的运输距离、运输费用以及二氧化碳排放量皆不同。订单具有相应的起点与终点，运输可途经若干个中间节点，可进行多次中转，也可直达。瞬息万变的市场使客户难以提前确定准确的需求量与送达时间，因此引入梯形模糊数表示模糊需求量与时间窗，对模糊货运量进行运输。在整个运输过程中以运输成本、碳排放成本最小，客户满意度最大为目标，对订单的运输路径进行优化，得出满意的运输方案。

图1 多式联运网络Fig.1 Multimodal transportation network

1.2 问题假设

本文模型基于以下假设：

1）在多式联运运输过程中相邻两个节点之间最多只能选择公路、水路、铁路其中一种运输方式。

2）每个运输节点没有转运能力限制，在运输过程中不考虑货损。

3）货物在节点转运完成即发往下一个目的地，不考虑仓储费用。

4）订单货物在运输过程中不可拆分，需一次性完整地从起点运输到终点。

5）多式联运网络中各节点互不限制，节点间不同的运输方式对应不同的运输路径。

6）除起点和终点外，其余运输节点处可进行中转作业，但需要产生相应的中转费用。

7）相同节点、相同运输方式下双向联通的运输路径距离相同。

1.3 符号与变量说明

参数与变量说明如表1～2 所示。

表1 参数说明Tab.1 Parameter description

表2 决策变量Tab.2 Decision variables

1.4 模糊量表示

模糊时间窗 客户可以接受货物到达的时间分为不同的时段，并且在不同的时段满意度不同。如图2［18］所示，当货物到达时间在[ET，LT]范围内时对应的客户满意度（Satisfaction）为1，这是客户最期待收货的时间窗；当客户的货物到达时间在[EET，LT]或[LT，LLT]范围内时，对应的客户满意度分别随时间呈线性上升和下降趋势；当货物到达时间超过[EET，LLT]范围内时，超出最大容忍时间上下限，客户不接受服务，客户满意度为0。因此用时间窗的隶属函数表示客户满意度，如式（1）所示：

图2 客户满意度函数Fig.2 Customer satisfaction function

为避免客户满意度过低造成客户流失，设置最低客户满意度β，从而得到货物运输的时间窗[Inf，Sup]，计算公式如下所示：

模糊需求量 客户的需求逐渐个性化，需求量也不再是固定不变的。在本文中，运用梯形模糊数来表示客户的模糊需求量。如图3 所示，e1和e4是最悲观和最乐观的估计，分别对应于实际需求量极少和极多的情况，出现的概率都极低。[e2，e3]对应于现实中需求量最有可能区间，最符合实际情况。不同决策者可通过改变模糊需求量偏好值θ对需求量的最有可能区间持有不同的观点，梯形模糊数在θ上为是在θ上的置信区间，其 中和分别为区间的上限和下限［17］，式（3）是模糊需求量的隶属函数：

图3 模糊需求量函数Fig.3 Fuzzy demand function

1.5 目标函数

1）碳排放成本：碳排放总量包括运输和中转过程中排放的二氧化碳，碳排放成本以碳排放总量与碳税值的乘积表示。

2）运输成本：运输成本包括运输固定成本、运输距离成本和中转成本。

3）客户满意度：以客户时间窗的隶属函数表示满意度，以最大化客户满意度为目标。

由于在运输过程中成本、碳排放量以及客户满意度的优化对于企业来说都极其重要，因此在多目标规划求解中本文针对上述3 个目标并行考虑。

1.6 约束条件

根据以上描述，相关约束条件表达如下：

式（7）～（9）表示节点流量守恒；式（10）为前后运输方式的连续性约束，即在节点i由运输方式m转换为l，则通过m到达i，通过l离开i；式（11）表示每批货物在同一节点只能转运一次；式（12）表示两相邻节点间最多只能采用一种运输方式；式（13）表示订单的起点和终点不转运；式（14）为最低客户满意度约束；式（15）是货物送达节点j所需时间的计算公式；式（16）为决策变量取值约束。

由于客户需求量具有模糊不确定性，约束（13）为模糊机会约束，上述模型为模糊机会约束规划。

2 模型求解

2.1 基于模糊可信度的模糊机会约束

模糊机会约束规划是一种基于可能性理论和模糊集合理论的不确定性数学规划，该理论表示，所做决策使模糊约束条件的可能性不小于给定的模糊需求量偏好值，可以将模糊机会约束条件转化为确定性的形式，也就是使模糊清晰化［19］，当给定一个确定数a和梯形模糊数=(b1，b2，b3，b4)，采用模糊可信度时，它们具有以下关系［20-21］：

根据式（17）对目标函数Z1、Z2和含有模糊数的约束（13）进行清晰化处理，由式（17）可知，当θ∈[0，0.5]时，Cr{a≥}≥θ即为a-b1≥2θ(b2-b1)，目标函数Z1、Z2和约束（15）中的可转换为式（18）：

当θ∈(0.5，1] 时，Cr{a≥}≥θ即为b4-2b3+a≥2θ(b4-b3)，目标函数Z1、Z2和约束（15）中的可转换为式（19）：

2.2 线性化处理

由于客户满意度为分段函数，无法直接使用DOCPLEX求解器对模型进行精确求解，因此本文需引入辅助变量，将客户满意度函数转换为线性函数。已知客户满意度为3 段连续函数，根据相关转换方法需引入3+1 个连续变量(Wi)与3 个0-1 变量(Rj)，同时连续变量(Wi)之和与0-1 变量(Rj)之和都需等于1，Wi的取值范围属于［0，1］，且Wi与Rj需满足严格的大小关系，具体表达式如下：

到达时间等于4 个连续变量Wi与4 个分段节点的相应乘积之和，客户满意度等于W2与W3之和，数学表达式如下：

3 自适应性NSGA⁃Ⅱ

传统的NSGA-Ⅱ（on-dominated Sorting Genetic Algorithm-Ⅱ）中采用固定的交叉、变异概率，会直接影响算法的收敛性。交叉概率越大，新个体产生的速度就越大，但遗传模式被破坏的概率也会越大；若交叉概率过小，会导致搜索过程缓慢甚至停滞不前。对于变异概率，过小不易产生新的个体；过大则会使算法变成了随机搜索算法。针对这一缺陷，本文基于自适应性对NSGA-Ⅱ进行改进，使交叉、变异概率能够自适应调整，避免走向局部最优解。

3.1 染色体编码与解码

多式联运路径优化问题涉及节点的选择、访问顺序以及运输方式的选择，因此本文采用三段式编码。假定运输网络中节点数为N，则编码长度为3N-1。如图4 所示，以6 个节点的运输网络为例，第一段为路径顺序编码，首末位分别为起点与终点，中间为其余节点。第二段为二进制编码，1 表示经过此节点；0 表示不经过此节点。第三段为运输方式编码，1、2、3 分别代表公路、铁路以及水路运输。

如图4 所示，根据第一段编码可知，起点和终点分别为节点2、6，根据第二段编码取1 的位点确定路径节点顺序，运输路径为2-1-6。舍去第二段编码的末位，根据其余取1 的位点确定运输方式，此图中运输方式为3-2，因此整条编码的含义为：2-水-1-铁-6。

图4 染色体编码Fig.4 Chromosome coding

3.2 初始化种群

本文基于编码规则采用随机生成的方式产生初始化种群，首先根据订单的起点和终点，分别确定第一段编码的首末位，中间随机生成其余节点。第二段首末位皆是1，中间随机生成0 或1，对节点进行选择。第三段编码则随机产生对应路径支持的运输方式，如此循环N次，就得到一个具有N个个体的初始种群。

3.3 快速非支配排序

快速非支配排序是对种群中的所有个体进行比较的过程，对于种群中每一个个体i，都分别对应两个参数Ui和Ri，Ui是种群中支配个体i的个体数量，Ri是被个体i支配的个体集合。若个体i的运输成本、碳排放成本都小于个体j，同时客户满意度大于个体j，则称个体i支配个体j，将Ui=0 的所有个体i存入非支配集合rank1 中，然后遍历rank1 中所有的个体i的支配个体集合Ri，将Ri中所有个体j的Uj减1，若满足Uj-1=0，则将个体j存入非支配集合rank2 中，以此类推，将所有个体存入不同层级的集合中。

3.4 遗传过程

1）选择操作。

小生境技术中的拥挤度可维持群体分布的多样性，拥挤度表示在种群中的给定点的周围个体的密度，非支配排序后处在相同层级的个体，拥挤度较大者会被优先选择，拥挤度计算公式如下：

其中：di是种群个体i的拥挤度距离，di，j表示个体i在第j个目标函数上的拥挤度距离，di等于个体i在所有目标函数上的拥挤距离之和。将与个体i具备相同非支配层级的个体的目标函数值升序排列，和分别为目标分量j的最大值与最小值，和为个体i在目标函数值j上的相邻值［22］。

本文选用轮盘赌选择，这是一种回放式随机采样方法，每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度值和的比例。对于本文的多目标模型，将分别计算运输成本、碳排放成本和客户满意度，三者的和作为个体的适应度。同时结合精英保留策略，用Pareto 非支配集替换新种群中适应度差的个体。

2）自适应交叉、变异概率。

交叉与变异概率（Pc、Pm）是影响遗传算法性能的关键，本文针对传统的交叉与变异概率按式（23）进行改进，使之能够自适应调整，避免走向局部最优解。其中：fmaxi、favgi和fmini分别是种群中第i个目标函数适应度的最大值、平均值和最小值；是待交叉的两个个体中适应度值较大者，fi为变异个体的适应度值；Pc、Pm分别为通过各个目标函数得出的Pci与Pmi的平均值，其余参数的取值范围与大小关系如下：1 >Pc1>Pc2>Pc3>0，1 >Pm1>Pm2>Pm3>0［22］。

3）交叉操作。

如图5 所示，根据编码规则第二段编码首末位皆为1，交叉无意义，同时为保证种群的多样性，则对第二段中间片段和第三段编码的全部片段进行交叉，即可改变路径又可改变运输方式，保证了种群的多样性。

图5 片段交叉Fig.5 Fragment crossover

4）变异操作。

本文采用染色体两点取逆变异，在路径编码中0-1 互逆，在运输方式编码中1-2-3 循环互逆，若父代染色体指定位点为1，则子代相应位点取2；同理若父代为2，子代取3；父代为3，子代为1。如图6 所示，对父代染色体的第二段中间和第三段首位两个位点进行取逆变异，由于第二段首末位必须为1，因此选取一个中间位点突变，而第三段的首位编码表示起点出发的运输方式，一定会纳入最终结果，因此第三段的首位是最佳突变点。

图6 取逆变异Fig.6 Reverse mutation

3.5 终止条件

终止准则是用于判断是否停止运行的条件，本文通过设定最大迭代次数，当进化代数达到最大迭代次数时算法结束，此时输出适应度值最低的解；否则，继续重复上述过程。算法流程如图7 所示。

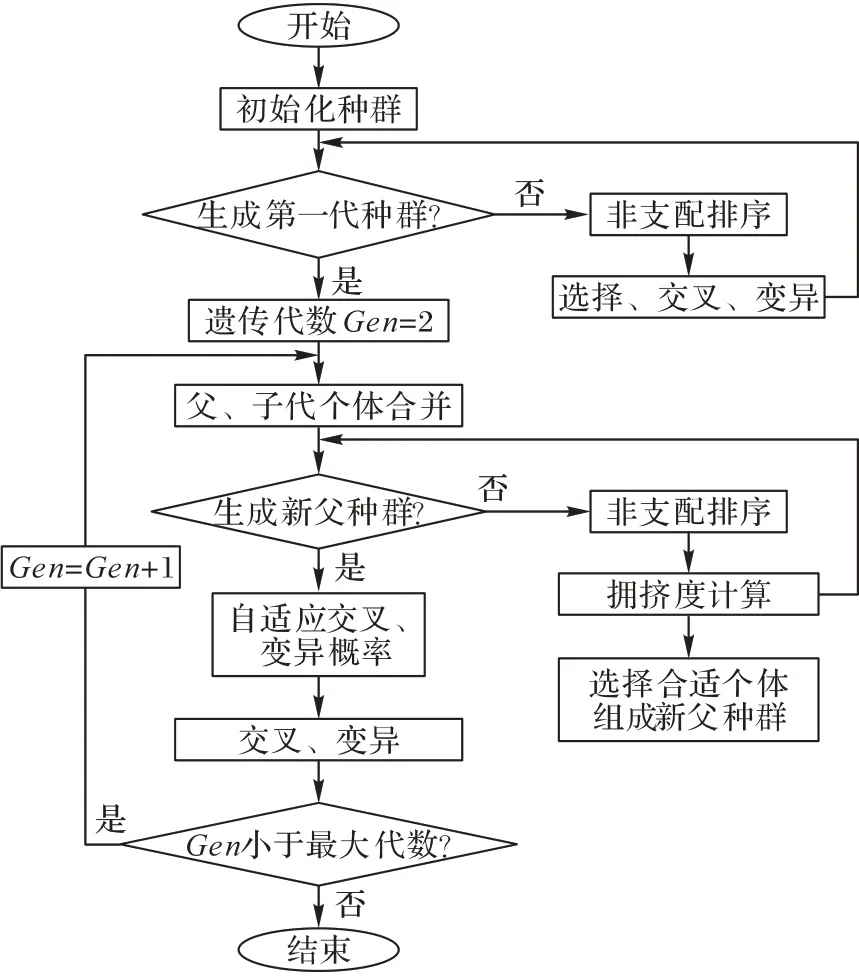
图7 本文算法流程Fig.7 Flowchart of the proposed algorithm

4 算例数据

在碳税政策的背景下，截至2018 年初，全国已有42 个国家和25 个地方管辖市通过碳排放交易体系或碳税对碳进行了定价。我国北京、天津、上海、重庆等7 个省市的碳交易市场十分活跃，成交均价范围在3.7～35.3 元/t［23］，因此本文的碳税值取0.015 元/kg，模糊需求量偏好值θ=0.6，运输方式、运输任务等参数如表3、4 所示。使用Matlab 2016b 实现算法程序，算法的参数：种群规模300，迭代次数为800，交叉变异概率参数：Pc1=0.9，Pc2=0.7，Pc3=0.5，Pm1=0.1，Pm2=0.05，Pm3=0.01。

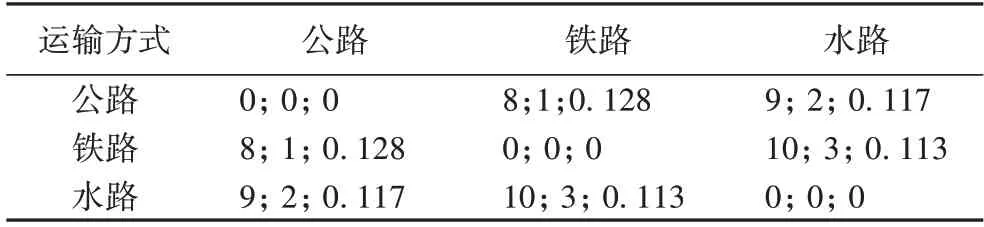
表3 运输方式参数Tab.3 Transportation mode parameters

表4 不同运输方式参数Tab.4 Parameters of different modes of transportation

5 结果分析

5.1 算法性能分析

通过DOCPLEX、NSGA-Ⅱ和自适应NSGA-Ⅱ分别对10～50 个节点的运输网络进行求解，订单起点和终点分别是1⁃N（N为最大节点数），模糊需求量与时间窗等运输参数见表5，NSGA-Ⅱ的交叉、变异概率为0.7、0.3。DOCPLEX 求解的目标函数值Z1min、Z2min和Z3max分别表示只考虑碳排放成本、运输成本的单目标下界值以及只考虑客户满意度的单目标上界值。NSGA-Ⅱ与自适应NSGA-Ⅱ求解的结果是运行20 次的平均值，Zi(i=1，2，3，4，5，6)分别表示基于算法所得到的目标函数值；gap1、gap2、gap3 分别表示自适应NSGA-Ⅱ与DOCPLEX 求得每个目标函数之间的差距百分比，同理，gap4、gap5、gap6 分别表示NSGA-Ⅱ与自适应NSGA-Ⅱ求得每个目标函数之间的差距百分比，结果对比见表6、7。

表5 订单相关信息参数Tab.5 Order-related information parameters

表6 DOCPLEX与自适应NSGA-Ⅱ的求解结果对比Tab.6 Comparison of solution results between DOCPLEX and adaptive NSGA-Ⅱ

表7 NSGA-Ⅱ与自适应NSGA-Ⅱ的求解结果对比Tab.7 Comparison of solution results between NSGA-Ⅱ and adaptive NSGA-Ⅱ

通过对比结果可知，当节点数量为10 时，DOCPLEX 的求解时间不到1 s，但随着节点数量的不断增加，求解时间直线上升，当节点数量达到50 时，求解时间超过1.5 min；但自适应NSGA-Ⅱ的求解时间只是小幅度增加，求解大规模算例时，具有很大优势。同时，自适应NSGA-Ⅱ求得的目标值与DOCPLEX 求得的单目标下界值差距不大，gap2 最大为9.24%，gap3 最大为4%，只有gap1 的差距百分较大，这是因为Z1与Z2目标函数之间的相关性太强，算法求得的目标函数值是整体最优值，且Z1与Z1min的数值相差不大，因此皆在正常范围之内。综合上述分析表明，自适应NSGA-Ⅱ算法对算例求解有效。

通过表6 可以看出，虽NSGA-Ⅱ算法的求解速度稍快于自适应NSGA-Ⅱ算法，但自适应NSGA-Ⅱ算法在目标优化方面相较于NSGA-Ⅱ算法有明显优势，gap4 与gap5 的最小值分别高达21.47% 与8.05%，且不同节点规模下自适应NSGA-Ⅱ求出的客户满意度全部大于等于NSGA-Ⅱ，这表明将自适应与NSGA-Ⅱ结合对多目标优化效果十分显著，证明了自适应NSGA-Ⅱ的科学性。

5.2 算例结果分析

本文选取30 个节点构成的运输网络，两个节点之间最多有公路、铁路、水路三种运输方式，基于自适应性NSGA-Ⅱ，分别对10 个运输订单进行求解，运输订单参数见表8。

表8 运输订单参数Tab.8 Transportation order parameters

具体结果如表9 所示，从结果中可以明显看出，客户满意度几乎全部高达100%，运输的时间十分合理；但运输方式皆为公路运输，猜测为碳税值过低，对碳排放成本约束太小所致，因此本文后续将对碳税值进行灵敏度分析，验证此猜想。

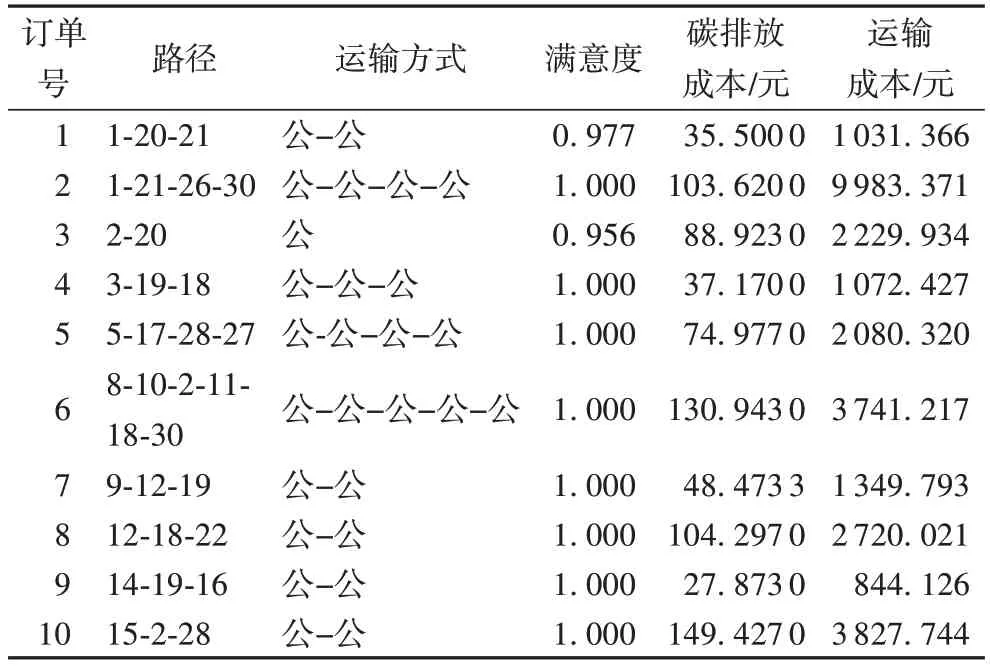
表9 不同订单的求解结果Tab.9 Solution results of different orders

5.3 碳税值灵敏度分析

基于上述猜想，现对碳税值进行灵敏度分析，从0 开始，逐级递增，分析碳税值变化运输方式、碳排放量等的影响，模糊需求量偏好值θ=0.6，具体求解结果见表10。

表10 碳税值变化下各运输订单路径结果Tab.10 Routing results for each transport order under changes in carbon tax value

根据结果绘制了以下折线图：图8 描述了10 个运输任务的运输方式频次变化；图9 描述了10 个运输订单以及订单3、8 的碳排放量随碳税值增大的变化趋势；图10 为10 个运输订单以及订单3、8 的总成本（碳排放成本与运输成本之和）变化趋势图。

1）从图8 可以明显看出，碳税值的提出可以有效促进“公转铁、公转水”。当碳税值为0～0.05 时，10 个运输订单全为公路运输，随着碳税值的增大，公路运输频次下降，转为铁路和水路运输，当碳税值达到1.5 元/kg 后，三种运输方式的频次趋于稳定。

图8 运输方式频次变化Fig.8 Frequency change of transportation mode

2）碳税值的提出对减少碳排放量效果显著。从图9 可以看出，当在碳税值为0～0.05 时，碳排放量达到顶峰，随着碳税值逐渐提高，公路运输逐渐转向铁路和水路运输，碳排放量也明显下降。由此可见，碳税值对节能减排、环境保护具有很大意义。

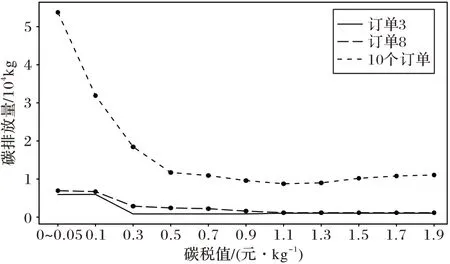
图9 碳排放量变化Fig.9 Carbon emission change

3）当碳税值增大到一定值后，运输方式与碳排放量的变化并不敏感。图9 的结果表明，碳税值与碳排放量并不会一直呈现负相关关系，当超出临界点后，碳排放量会趋于稳定，甚至有所回升。但图10 表明，随着碳税值增大，总成本一直上升。因此，不能一味地追求高碳税值，不仅不能减少碳排放量还会对企业造成过高的成本。

图10 总成本变化Fig.10 Total cost change

4）我国制定的碳税值较低，对企业与货运人约束十分有限。已有大量文献表明我国的碳税值远低于国外，欧盟碳价格最高35 欧元/t，约合人民币350 元/t，而我国的碳税值成交均价范围是0.003 7～0.035 3 元/kg［22］。由图8 可知，在此范围内，以公路运输为主，碳排放量达到顶峰。因此，我国应当整体提高碳税值，加强对企业和货运人的约束，促进“公转铁、公转水”。

5.4 模糊需求量偏好值灵敏度分析

在模糊机会约束中，模糊需求量偏好值由决策者主观设置，因此有必要对模糊需求量偏好值进行灵敏度分析，探讨模糊需求量偏好值对优化结果的影响，为企业确定合适的偏好值。

基于上述碳税值分析，在此分析中对碳税值取0.3 元/kg。模糊需求量偏好值从0.1 开始，步长0.1，逐级递增到1，如图11 所示，根据求解结果描绘了10 个运输订单的总成本随模糊需求量偏好值增大的变化情况。由图可知，当模糊需求量偏好值小于0.5 或大于0.6 时，总成本上升得较为平缓，在0.5～0.6，总成本上升得最为显著，即当模糊需求量偏好值处于0.5～0.6 时，对总成本的影响最大。即模糊需求量偏好值越高，实际运输货物量越大，满足客户需求量的概率越大，但成本也会随之增大，运输经济性与需求可靠性两者不可兼得。因此，站在企业开源节流的角度，0.5 为企业最合适的偏好值水平，既节约了成本又能基本满足客户需求。

图11 总成本与模糊需求量偏好值的关系Fig.11 Relationship between total cost and fuzzy demand preference value

6 结语

本文选用梯形模糊数表示时间窗与需求量，以时间窗的隶属函数表示客户满意度，提高了时间窗与需求量变化的灵活性。建立了多目标模糊机会约束模型，对含有30 个节点的多式联运网络建立算例，运用自适应性NSGA-Ⅱ求解得出优化结果，通过分析具体结果验证了算法的有效性，并探究了碳税值与模糊需求量偏好值变化对优化结果的影响；但对于整体环境不确定性下的多式联运路径优化问题还需进一步研究。