多样性表示的深度子空间聚类算法

马志峰，于俊洋，王龙葛*

（1.河南大学 软件学院，河南 开封 475004；2.河南省智能数据处理工程研究中心（河南大学），河南 开封 475004）

0 引言

聚类分析一直以来都是数据挖掘的主要任务之一，常见的聚类算法分为很多种，例如基于划分的聚类算法、基于层次的聚类算法、基于神经网络的聚类算法和基于模糊的聚类算法等，其中不乏一些优秀的算法，例如偏差稀疏模糊C 均值（Deviation-Sparse Fuzzy C-Means，DSFCM）聚类算法［1］和基于块的模糊局部相似C 均值（Patch-based Fuzzy Local Similarity C-Means，PFLSCM）聚类算法［2］，这些算法都是在模糊C 均值（Fuzzy C-Means，FCM）聚类算法［3］的基础上获得改进并成功应用于图像分割领域。近年来，随着机器学习和深度学习的发展，子空间聚类成为专家和学者研究的热点，在图像分割［4-5］、人脸聚类［6-7］和推荐系统［8-9］的实际应用中，传统聚类算法对高维数据往往难以达到理想的聚类效果。子空间聚类是解决这些高维数据聚类的有效方法之一，子空间聚类的任务就是将来自不同子空间的高维数据分割到本质上所属的低维子空间。

研究者提出了大量的传统子空间聚类算法，其中基于谱聚类的算法［10］由于具有无须预先设定子空间的维度以及不受初始化影响的优势而越来越受到关注，例如稀疏子空间聚类（Sparse Subspace Clustering，SSC）［11-12］、低秩表示（Low Rank Representation，LRR）［13-14］等。这类算法通常将问题分为三步：首先，通过自表示学习从数据中学习一个表示数据对相似性的自表示矩阵C；然后，通过自表示矩阵构造相似度矩阵W；最后，将相似度矩阵应用到谱聚类算法得到最终的聚类结果。然而这些传统算法的目标只在于学习样本的低维表示结构而忽略了局部距离关系，而且每一个样本的表示系数不能清晰地展示样本之间的相似度。因此，这些传统算法没有很好的可解释性并且不能揭示数据的内在结构。

深度子 空间聚类（Deep Subspace Clustering，DSC）网络［15］在编码器与解码器间加入自表示层，在编码器映射的低维非线性空间中学习自表示系数矩阵，该网络可以对具有复杂或非线性潜在结构的数据进行有效聚类，从而弥补了传统子空间聚类算法只能探索线性数据关系的弊端；深度对抗子空间聚类（Deep Adversarial Subspace Clustering，DASC）［16］采用基于子空间特异性的对抗学习网络来监督样本的表示；神经协同过滤子空间聚类（Neural Collaborative Subspace Clustering，NCSC）［17］将子空间聚类问题重新定义为分类问题，将谱聚类步骤从经典的DSC 网络中解放出来；自监督卷积子空间聚类网络（Self-Supervised Convolutional Subspace Clustering Network，S2ConvSCN）［18］在DSC 的基础上加入了自监督模块，将自表示系数矩阵的学习与谱聚类结合，首次利用聚类标签信息监督自表示系数矩阵的学习；在基于深度自编码器的子空间聚类中，较浅的层学习更多的像素级信息，较深的层提取更多的语义级或抽象级信息，输入数据的多尺度特征内在地嵌入在深度自编码器的不同层中。上述工作在学习自表示矩阵时只考虑了从最深层提取的特征的自表示学习，而忽略了较浅层次中有用的特征以及深度自编码器中嵌入的多尺度信息的融合，浪费了大量现成的、但很有用的信息，总是无法达到理想的聚类性能。多层次表示的深度子空间聚类（Multi-Level Representation learning for Deep Subspace Clustering，MLRDSC）［19］通过组合不同网络层的自表示系数矩阵，融合了不同尺度的信息，提高了聚类效果，然而此算法没有充分考虑不同尺度信息的多样性。

为了得到原始数据更好的特征表示，本文所提算法从充分挖掘多个中间层数据的多样性表示、探索不同尺度特征之间的互补信息的角度出发，增强聚类效果。本文工作与其他算法的不同点主要体现在：其他算法主要是为了获得更好的相似度矩阵，很少从原始数据的特征表示出发；而本文工作的目的与创新主要是为了增加多层次特征表示之间的互补性，减少多层次特征表示之间的冗余信息，从而获得原始数据更好的特征表示，即增加特征表示的多样性，增强聚类效果。本文的主要工作如下：

1）建立了深度自编码器中不同层次特征衡量多样性表示的模型。

2）在基于深度自编码器的网络结构中引入多样性表示模块，挖掘有利于提升聚类效果的图像特征。

3）更新了损失函数表示项，有效融合多层次表示的底层子空间。

4）在多个常用聚类数据集上进行了多次实验，实验结果验证了本文算法具有更优的聚类效果。

1 相关工作

1.1 多层次表示的深度子空间聚类模型

在基于深度自编码器的网络结构中常利用重构损失约束自编码器中的网络参数，确保经过编码器编码得到的特征数据能通过解码器还原回原始数据。重构损失的表现形式如式（1）所示：

其中：‖·‖F表示F 范数，X表示原始输入数据，表示经过深度自编码器获得的重构数据。

MLRDSC 充分利用了自编码器网络中的多个中间层特征数据，利用自表示层学习中间层数据共享和私有的自表示系数矩阵，融合了多个中间层数据的有用信息，从而提高了聚类效果。在MLRDSC 中，为了获取每个层共享和私有的自表示系数矩阵，引入如式（2）所示的自表示损失项：

其中：L表示网络深度；θ表示深度自编码器网络中的参数，包含θe、C、Di和θd，θe表示编码器中的参数，C表示各层共享的自表示系数矩阵，Di表示各层私有的自表示系数矩阵，θd表示解码器中的参数；表示原始数据经过编码器得到的在子空间中的数据表示。

除此之外，为了促进编码器不同层次的自表示系数的学习，对于各层数据私有的自表示系数矩阵Di施加F 范数，确保相似度矩阵与各层数据都有关联。对于各层数据共享的自表示系数矩阵C施加l1范数来确保C的稀疏性，如式（3）、（4）所示：

其中：‖·‖1计算其输入矩阵的绝对值之和；Q∈RN×K是一个伪标签矩阵，即聚类得到的标签矩阵。

然而MLRDSC并没有考虑深度自编码器的不同层级学习的特征间的差异性和特征表示之间的多样性。为了增强深度自编码器的学习能力，得到原始数据更好的特征表示，本文算法从增加原始数据特征表示多样性的角度，在深度自编码器学习到的低层和高层特征之间采用希尔伯特-施密特独立性准则（Hilbert-Schmidt Independence Criterion，HSIC）［20-21］来衡量特征表示的多样性，并反馈给深度自编码器，使其学习更多有利于提升聚类效果的特征。

1.2 希尔伯特-施密特独立性准则

高独立性意味着高多样性，本文将来自两个不同尺度的特征作为二元可观测变量空间，采用HSIC 来衡量二元可观测变量的独立性，用高独立性来表示高多样性。主要原因：1）HSIC 通过将变量映射到再生核希尔伯特空间（Reproducing Kernel Hilbert Space，RKHS）来测量相关性，使得在该空间中测量的相关性对应于原始分布之间的更复杂、更高阶的非线性相关性；2）HSIC 无需显式估计随机变量的联合分布，即可估计变量之间的相关性；3）HSIC 在计算上等于矩阵的乘积的迹。本文使用HSIC 来惩罚不同尺度特征表示中数据的相关性来提升深度编码器的学习能力，增加特征表示的多样性。

HSIC 与交叉协方差密切相关。首先，假设X，Y是两个可观测变量空间，定义一个非线性映射空间ϕ(x) ∈F，F 属于RKHS 且x∈X，再定义一个φ(y) ∈G，G同样属于RKHS且y∈Y。相应的核函数如式（5）（6）所示：

交叉协方差算子如式（7）所示：

其中：μx=E(ϕ(x))，μy=E(φ(y))，⊗表示张量积。Cxy可以看作Hilbert-Schmidt 算子，然后将F 范数扩展到该算子上，得到Hilbert-Schmidt 范数，将该范数平方即可得到Hilbert-Schmidt 独立性准则，如式（8）所示：

其中‖A‖HS表示矩阵A的Hilbert-Schmidt 范数，如式（9）所示：

最终，得到关于HSIC 的定义表达式如式（10）所示，详细推导过程可参考文献［22］。

其中：K1、K2表示核矩阵；H使得核矩阵能够在特征空间中具有零均值，hij表示H中元素，hij=δij-1/N。

2 本文工作

为了提高自编码器的学习能力，提升自编码器学习到的不同尺度特征之间的特征多样性表示，探索低层特征和高层特征之间的互补信息，本文在MLRDSC 的基础上提出了多样性表示的深度子空间聚类（Diversity Represented Deep Subspace Clustering，DRDSC）算法，设计了衡量不同层次特征多样性衡量的模型，并将特征多样性规范化项应用于对多层次深度子空间聚类网络参数优化。

2.1 多样性表示

本文将不同尺度特征的多样性表示反馈给编码器网络，提出了衡量不同层次特征多样性表示的模型，在衡量特征多样性表示时，要求同一样本数据的低层和高层特征的数量相同。设计的方案是将编码器提取到的图像的低层和高层特征展开为一维特征空间，然后隔行提取特征，取得使低层与高层特征数量相同。间隔采样特征是根据图像自编码器在图像低层和图像高层所提取的特征数量所决定的，本文提出的间隔特征数量的计算模型如式（11）所示：

其中：Count(Zi)、Count(Zj)分别代表第i和j层特征编码器提取到的图像特征总数；d代表间隔采样的特征数。采用HSIC来衡量不同尺度特征的多样性表示，用高独立性来表示高多样性。计算过程如图1 所示（以d=2 为例），假设、和分别表示第i个样本数据经过第1、2、3 层卷积得到的特征数据。为了衡量和的多样性表示，本文将变换为一维特征数据然后间隔d行采样得到，然后计算和的多样性表示以代表原始特征的多样性表示，采用同样的方法衡量和以及和的多样性表示。

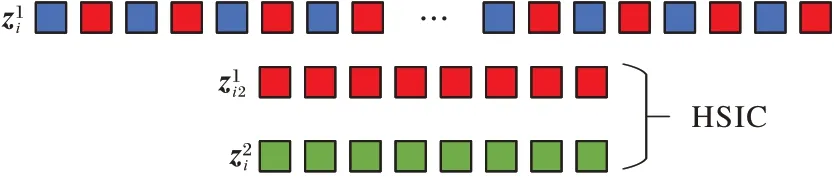
图1 衡量特征多样性表示Fig.1 Measuring diversity representation of features

2.2 网络结构

DRDSC 的网络结构由编码器模块、多样性表示模块、自表示模块、谱聚类模块和解码器模块五部分构成，如图2 所示。编码器模块负责提取原始数据的尺度特征；多样性表示模块负责增加原始数据特征表示多样性；自表示模块负责获取自表示矩阵，从而计算相似度矩阵；谱聚类模块负责由相似度矩阵计算聚类标签；解码器模块负责将子空间特征恢复为原始空间数据。本文在深度自编码器网络结构获取的不同层次特征间施加多样性表示模块，目的是使自编码器在学习过程中学习更多的有用特征。假设N个数据样本构成原始输入矩阵为X，设由三层编码器网络提取到的低层和高层特征分别为Z1、Z2和Z3。多样性表示模块首先将不同层次特征进行抽样处理；然后，用HSIC 衡量不同层次特征的多样性表示；最后，将不同层次特征相关性反馈给自编码器网络，使得网络在学习过程中提升编码器网络提取特征的多样性，得到原始数据更多样、更好的特征表示。

图2 DRDSC网络结构Fig.2 Network structure of DRDSC

2.3 目标函数

根据DRDSC 的网络结构，本文的目标函数一共包含四部分：重构损失、自表示损失、多样性表示规范化项和其他约束，其中多样性表示规范化项是研究的重点。

为了衡量不同层次图像特征的多样性表示，本文引入了多样性表示规范化项。首先，深度自编码器获取原始数据的不同层次特征表示Zi；然后，将不同层次特征Zi输入到多样性表示模型中计算多样性表示规范化项；最后，将结果反馈给深度自编码器网络。多样性表示规范化项是对编码器中的网络参数施加约束，增加特征表示的多样性。多样性表示规范化项的表现形式如式（12）所示：

其中：Ki和Kj分别表示Zi和Zj的核矩阵，本文采用正交核，即Kj=ZjTZj。H使得核矩阵能够在特征空间中具有零均值，hij=δij-1/N。

在基于MLRDC 算法的基础上，综合式（1）～（4）、（12）和（13），得到本文优化后的损失函数，如式（14）所示：

s.t.diag (C+Di)=0；i∈{1，2，…，L}

其中：λ1，λ2，λ3，λ4>0 是平衡各项做出贡献的超参数，采用标准的反向传播（Back Propagation，BP）算法来获得式（14）的解。根据求得的C和，创建相似度矩阵W，如式（15）所示：

最后，将W输入到谱聚类算法中来获得聚类标签。

DRDSC 整体算法流程如算法1 所示。

算法1 DRDSC。

输入 原始样本数据X，样本标签数据Q，Q的更新周期T0，最大迭代次数Tmax，随机初始化自编码器网络参数；

输出 聚类结果Q。

3 实验与分析

3.1 数据集

为了客观评估和比较本文算法与其他聚类算法的性能，在数据集Extended Yale B、ORL、COIL20 和Umist［23-25］上分别进行了实验。上述4 个数据集作为子空间聚类的基准数据集，曾广泛应用于其他子空间聚类算法来评估子空间聚类的性能。每个数据集的示例数据如图3 所示。

图3 聚类数据集Fig.3 Clustered datasets

数据集Extended Yale B 包含2 432 张正面人脸图像，分别由38 个不同的人拍摄，每个人有64 张在不同光照和不同姿势下拍摄的照片。

数据集ORL 由400 张大小为112×92 的人脸图像，分别来自40 个不同的人，每个人有10 张不同姿势、光照条件和面部表情的照片。本文将图像原始尺寸降维到32×32，因为该数据集面部表情变化较大，且每个人的图像数据相当少，所以在该数据集上的子空间聚类非常具有挑战性。

数据集COIL20 被广泛用于不同类型的聚类算法，它是由包含20 个目标对象的1 440 张图像构成，其中每个目标对象由72 张在黑色背景下以5 度的间隔拍摄的照片构成。

数据集Umist 包含了20 个人的480 张图片，每张照片的姿势变化都比较大，本文采样到32×32 的尺寸。

3.2 实验过程

在数据集Extended Yale B 上，对连续的不同数量的聚类目标进行了多次实验，取结果的平均数和中位数进行对比。为了增加对比性，分别将该数据集在MLRDSC 与DRDSC 上进行实验，两者的超参数λ1、λ2、λ3设置相同，DRDSC 的超参数λ4统一设置为1×10-2，聚类标签Q的更新周期设置为T=100，最大迭代次数设置为1 500。

数据集Extended Yale B 前5 个聚类目标在算法DSC、MLRDSC、DRDSC 上学习到的自表示系数矩阵可视化如图4所示。

图4 自表示系数矩阵可视化Fig.4 Self-represention coefficient matrix visualization

在数据集ORL 上的实验，实验中使用的参数设置为λ1=1，λ2=1×10-2，λ3=1×10-1，λ4=1×10-4，T=10，最大迭代次数设置为580。

对于数据集COIL20，文献［15-16］算法使用一层卷积自动编码器来学习特征表示，滤波器数量通常为15，但这并不能体现多层次特征融合与探索多层次特征的多样性。为了体现DRDSC 的优势，本实验在保留第一层的设置的基础上又增加了一层编码器。COIL20 数据集的参数设置如下：λ1=10，λ2=1，λ3=90，λ4=5，T=5，最大迭代次数设置为60。

对于数据集Umist 上的实验参数设置为λ1=10，λ2=1，λ3=1，λ4=1×10-2，T=10，最大迭代次数设置为190。各数据集网络结构层数设置、滤波器数量、滤波器大小详细设置如表1 所示。

表1 不同数据集的网络结构参数Tab.1 Network structure parameters of different datasets

为了分析不同损失项对聚类效果的影响，进行了参数设置进行了研究。首先固定所有超参数初始值为1，在参数λ1进行调整时，固定其他参数，在｛10-4，10-3，10-2，10-1，1，10｝范围内调整λ1的取值，获得λ1的相对最佳值后，固定λ1，以相同方式调整其他参数，直到获得所有参数的妥协最佳值。为了更进一步得到更好的聚类效果，本实验又对λ1～λ4的值在小范围整数倍范围内调整。以COIL20 数据集为例，首先在｛10-4，10-3，10-2，10-1，1，10｝的范围内调整λ1～λ4以取得较好的聚类效果，例如λ1～λ4分别取λ1=10，λ2=1，λ3=10，λ4=1，为了更进一步取得更好的参数设置，以λ1=10 来说，继续在λ1的整数倍[3，5，7，9]范围内调整。其他参数的调参过程与λ1类似，直至实验取得最好的参数设置λ1=10，λ2=1，λ3=90，λ4=5。

3.3 实验结论

在数据集Extended Yale B 上的实验结果如表2 所示，由表2 可以看出，DRDSC 与LRR［11］、SSC［13］、核稀疏子空间聚类（Kernel Sparse Subspace Clustering，KSSC）［26］、高效稠密子空间聚类（Efficient Dense Subspace Clustering，EDSC）［27］、AE+EDSC、DSC［15］、S2ConvSCN［17］、MLRDSC［18］相比在聚类错误率上取得了更好的结果。在连续20、25、30、35、38 个目标上进行的聚类实验平均错误率分别达到0.98%、1.00%、1.13%、1.42%和1.23%，聚类效果均优于MLRDSC，各聚类实验在Extended Yale B 上的平均错误率如图5 所示。

图5 Extended Yale B数据集上的平均错误率Fig.5 Average error rate on Extended Yale B dataset

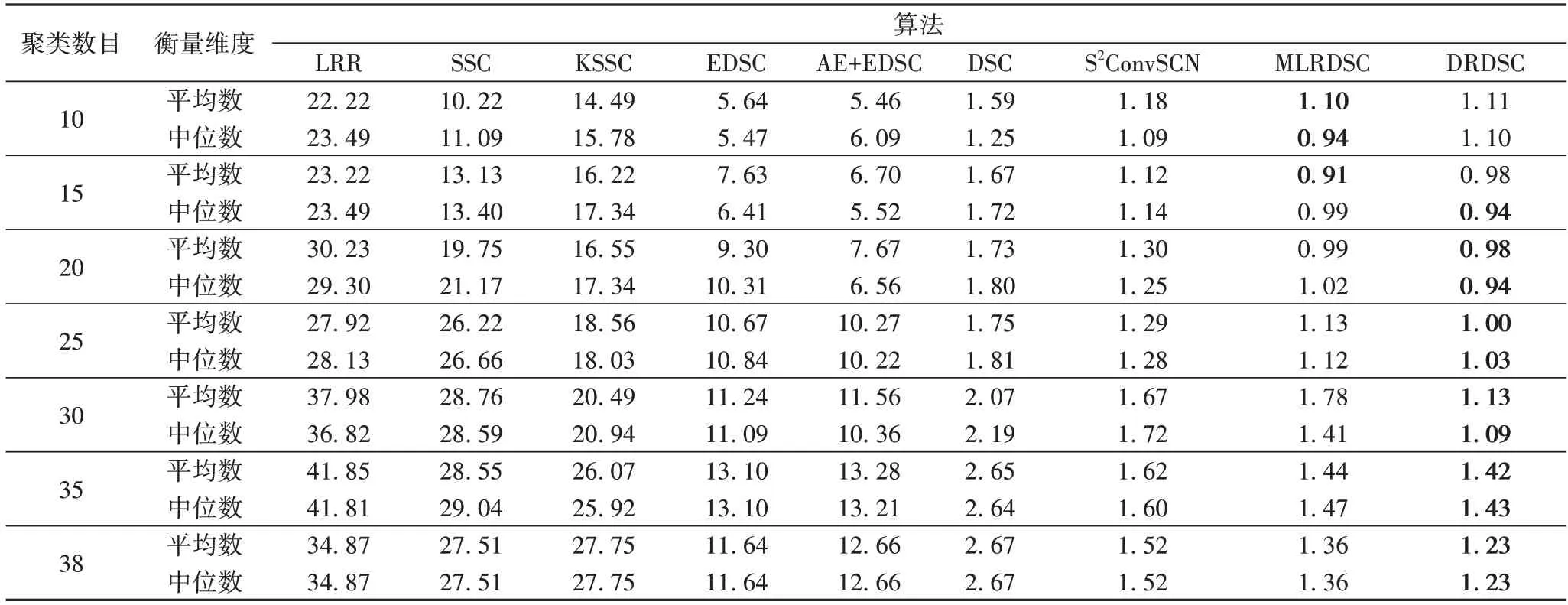
表2 Extended Yale B数据集上的聚类错误率结果对比 单位：%Tab.2 Clustering error rate result comparison on Extended Yale B dataset unit：%

DRDSC 在ORL、COIL20 和Umist 数据集的结果如表3所示。

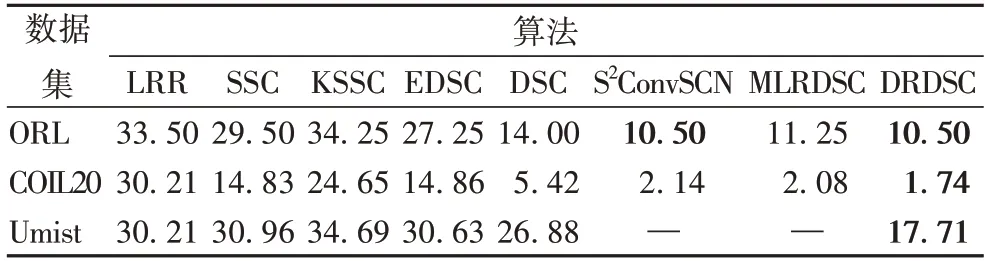
表3 ORL、COIL20和Umist数据集上的聚类错误率结果对比 单位：%Tab.3 Clustering error rate result comparison on ORL，COIL20 and Umist datasets unit：%

从表3 可以看出，在ORL 数据集上的聚类错误率与S2ConvSCN 持平，均达到10.50%，与MLRDSC 相比错误率降低了0.75 个百分点；在COIL20 上的实验结果表明，本文在增加了一层卷积编码器的网络结构上，取得了更好的聚类结果；在Umist 上的实验结果表明，DRDSC 与KSSC、EDSC 和DSC 相比在错误率上分别降低了16.98、12.92 和9.17 个百分点，聚类效果有了相对较大提升。

4 结语

本文针对深度自编码器网络结构中不同层次特征互补信息挖掘困难的问题，提出了一种探索不同尺度特征多样性表示的深度子空间聚类算法，为基于深度自编码器聚类任务中，挖掘原始数据特征表示多样性与不同层次特征互补信息提供了解决方案。在常用的聚类数据集Extended Yale B、ORL、COIL20 和Umist 上的聚类错误率分别达到1.23%、10.50%、1.74%和17.71%，验证了本文提出算法的有效性。在实际应用中，数据分析涉及到的高维数据，往往具有多种表现形式，在未来的工作中，会进一步探索多尺度信息的一致性和多样性对深度多模态子空间聚类的影响。