气体静压主轴模态仿真分析及试验研究

王玉伟 吴东旭 索奇 肖北川 王辉

（通用技术集团机床工程研究院有限公司，北京 101300）

目前，超精密机床中的运动部件普遍采用流体静压支撑的方式将固定件与运动件隔开，避免直接接触，减小摩擦阻力。流体在固定件与运动件之间充当润滑介质，此种方式提高了运动部件的运动精度[1]。其中当所需承载力要求不高时，多采用气体静压支撑的方式，且气体作为流动介质具有温升小、精度高的优势[2-3]。目前国外生产气体静压主轴的厂家主要以美国AMETEK Precitech、Professional Instruments及日本芝浦机械为代表，其生产的气体静压主轴回转精度均达到了20 nm[4-5]。国内从事研究气体静压主轴的单位主要有通用技术集团机床工程研究院有限公司、哈尔滨工业大学、北京航空精密机械研究所、中国工程物理研究院机械制造工艺研究所及北京海普瑞森超精密技术有限公司等。

主轴部件作为机床的核心功能部件，其运动精度决定了加工件的质量，主轴在不同速度下工作时，当工作频率与某阶固有频率相接近时会引发主轴部件产生共振。主轴部件受其结构形式、约束方式的影响，从低频到高频分布有多阶固有频率。固有频率引发的系统共振会造成气体静压主轴旋转中心偏移，气膜间隙发生变化，气膜压力分布不均匀，不稳定振荡且噪声大等问题，进而加大运动误差，造成加工件表面粗糙度及面形精度降低，影响超精密加工质量[6-7]。为避免产生上述问题，本文从有限元仿真分析及试验测试入手，对有限元模型中设置的弹簧刚度系统进行力学验证，通过主轴部件静力学仿真与试验测试结合分析，对动力学计算中的弹簧刚度进行修正；其次对电机转子与定子间电磁力对主轴转子自由度的影响进行研究，使得加载的边界条件更精确，保证有限元模型中的约束符合实际，以获取准确的模态参数。在仿真的基础上通过锤击模态测试试验进一步验证结构模态参数信息。基于有限元计算结果，可以更好地确定试验中传感器布局位置，避开模态节点，同时确定测试频率范围，提高测试精度。利用多参考点布局的试验手段，在主轴转子及外壳均匀布局多个传感器，每个传感器位置在不同方向进行外界激励，以此充分获取模态信息，同时利用检查相干函数的方式，获得高质量测试数据。通过仿真与试验结果对比，最终确定主轴部件各阶模态参数，作为机床工作过程中选择合适工作转速的依据，有效选择避开系统共振频率，保证主轴稳定工作，同时为进一步改进主轴部件结构提供参考依据。

1 主轴结构

本主轴采用多孔石墨双半球支撑结构，在多孔石墨轴瓦与主轴半球轴承之间形成气膜，气膜厚度在10～15 μm，外界供气压力为0.4～0.6 MPa，主轴部件主要由外壳、轴瓦、主轴转子、多孔石墨、半球轴承和内装电机等部分组成，如图1所示，主轴转子上左右两侧各安装一个半球轴承。两个半球轴承分别与固定在外壳上的两个多孔石墨轴瓦配合完成对主轴转子系统的气浮支撑。为分析结构质量对主轴模态的影响，简化后的有限元模型共采用两种方式：（1）只保留主轴转子结构的有限元模型，如图2所示。（2）留主轴全部零部件的有限元模型，如图1所示，对其进行有限元仿真计算及对比分析。

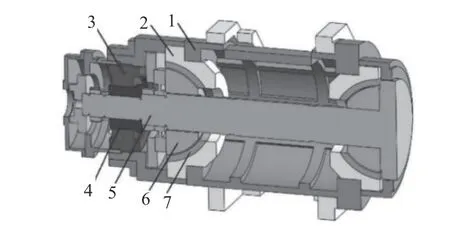
图1 主轴部件结构图

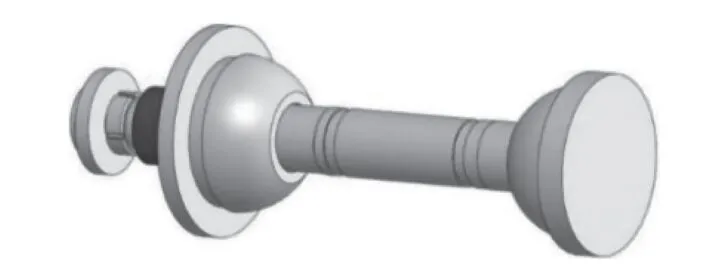
图2 主轴转子结构图

2 模态仿真

2.1 边界条件分析

主轴有限元模型中应重点考虑的边界条件集中在电机与主轴转子以及多孔石墨球瓦与半球轴承之间的装配约束关系上。电机定子与转子之间的电磁力及球瓦与半球轴承之间存在的气膜承载力为系统零件之间的约束条件，直接影响系统刚体自由度及内部刚度，因此在装配模型中主要针对以上两种情况需要定义的边界条件进行研究，零部件之间的绑定约束及外壳底座的固定约束不再展开论述。

2.1.1 弹簧刚度设置

气膜所产生的刚度在有限元模型中简化为压缩-拉伸弹簧单元，弹簧单元的刚度数值通过前期试验测试获得，其中主轴轴向气膜刚度为180 N/μm，径向刚度为90 N/μm。为确定在有限元中加载的弹簧单元刚度数值正确，对主轴转子进行弹簧加载的力学验证。对有限元模型中轴瓦与半球轴承匹配的两端球面上分别添加4个弹簧，共8个弹簧，如图3所示。若按照实际测得的气膜刚度结果直接转化为弹簧刚度数值，即单个弹簧的刚度值设置为180 N/μm或90 N/μm，则需要验证设置是否合理。

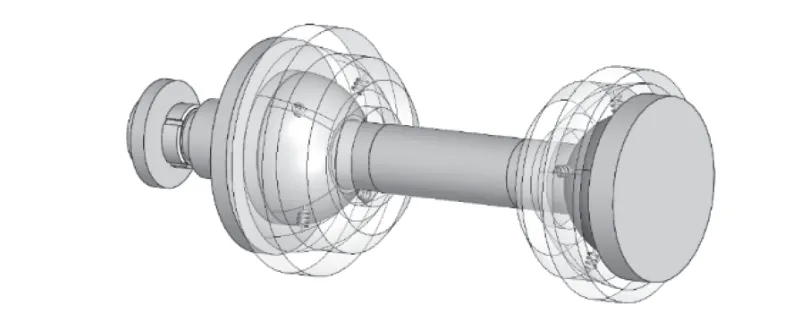
图3 弹簧加载图

在主轴右端连接卡盘位置处的轴向（Y方向）及径向（X方向）施加100 N的力进行计算，查看主轴转子在轴向及径向上的变形量。根据仿真分析中主轴转子变形量与加载力计算得出的气膜刚度值，并与起初加载到有限元中的弹簧刚度数值作比较，查看弹簧刚度设置是否需要进行调整。主轴转子受力后的有限元应变结果云图如图4所示。

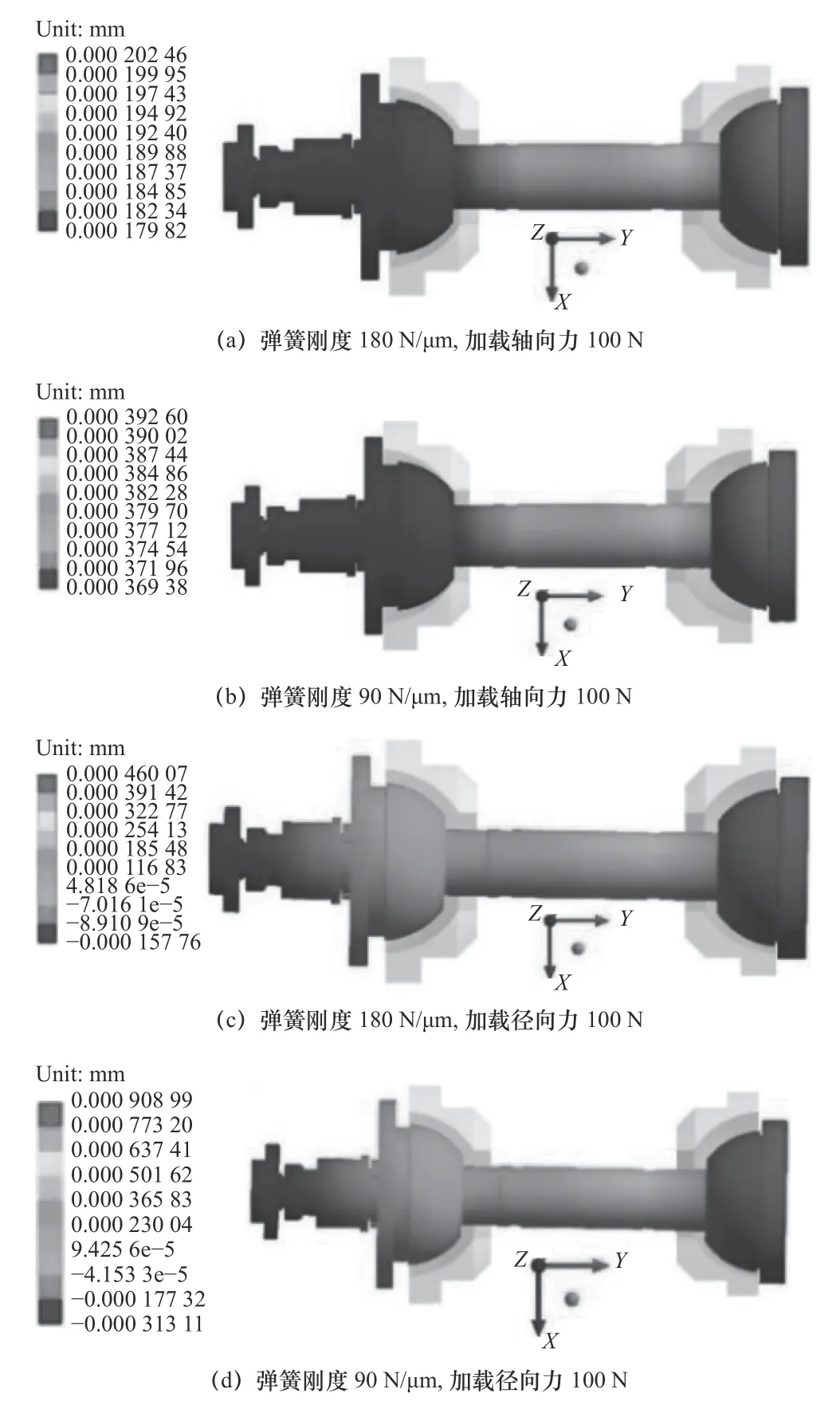
图4 不同弹簧刚度下受力变形云

主轴转子因自身弹性变形的影响，使得左右两端半球轴承处的弹簧变形量不一致，因作用力加载在主轴右端，为减小主轴转子弹性变形对计算刚度的影响，变形结果取自右端半球轴承处半球轴承的变形量。根据作用力及变形量计算的气膜刚度值如表1所示。

表1 不同弹簧刚度及受力下的总体计算刚度

上述结果表明，在球面添加弹簧且在两个球面共均布8个弹簧时，轴向方向气膜刚度值为加载的单个弹簧刚度的3倍，径向方向气膜刚度值为加载的单个弹簧刚度的1.5倍。根据主轴实际试验获得的轴向气膜刚度180 N/μm及径向气膜刚度90 N/μm，对有限元模型中添加的弹簧单元进行修正，设置的单个弹簧刚度值应为60 N/μm。

为进一步验证修正后的弹簧刚度，将单个弹簧刚度值为60 N/μm的弹簧按同样方式加载至轴瓦与半球之间，左右两侧分别加载4个总共8个弹簧，同样对主轴右端的轴向和径向分别施加100 N的力，通过静力学计算得出在右端轴承处的轴向及径向变形分别为0.56 μm及1.11 μm，如图5所示，此时计算得出的轴向及径向刚度分别为178.6 N/μm及90.1 N/μm，与试验测量获得的180 N/μm及90 N/μm基本一致。

图5 加载修正后弹簧的主轴变形

2.1.2 电机转子约束

电机运行过程中通过电磁力驱动电机转子进行转动，且电机定子与转子之间的气隙一般在0.1 mm左右[8]，电机转子所受电磁力使转子产生切向力及径向力。切向力主要驱动转子进行转动[9-10]，径向力沿着转子一周有可能会带来转子偏心问题。因本气浮轴承回转精度在50 nm，故相对于电机转子与定子之间的气隙及受力，电机转子在径向、轴向及沿轴向回转的方向简化为自由约束边界条件，同时电机转子表面在沿轴向长度方向受均匀切向力的约束。除绕转子轴线方向的转动为自由约束外，其余两个方向无法进行转动，因此电机转子的边界条件总体简化为在X、Y、Z、RZ这4个方向无约束，同时限制RX、RY两个方向的转动，如图6所示。

图6 电机及气膜处边界约束情况

2.2 结果分析

2.2.1 仅保留主轴转子结构的仿真结果

以轴瓦为支撑体，主轴转子结构的前六阶固有频率、参与系数及有效参与质量信息如表2所示，其中参与系数的含义为某振型在特定方向上参与振动的程度，某一方向的参与系数越大，则表明在这个方向上受到动载荷的作用时结构的振动响应越大。有效质量是指在某个方向参与振动的质量与结构总质量之比，理想情况下每个方向的所有有效质量之和等于结构的总质量，但实际中要取决于提取的模态阶数是否充足。主轴转子前六阶的模态振型趋势如图7所示。

图7 主轴转子前六阶模态振型趋势

表2 主轴转子仿真结果模态参数

上述结果表明，第一阶固有频率为1.5 Hz，接近0，参与系数在绕着Y转动方向为1，参与的有效质量达到0.99，因此第一阶振型趋势为主轴转子绕着主轴轴线进行回转；第二、三阶分别为277 Hz和279 Hz，这两阶振型相似，参与系数分在Z、X移动方向为1，参与质量都是0.91，因此为重根模态，振型趋势都为在主轴径向方向进行整体移动；第四阶为316 Hz，参与系数在Y移动方向为1，参与的有效质量为0.99，振型趋势为沿着主轴轴线方向整体移动；第五、六阶分别为384 Hz，385 Hz，从参与系数及有效质量发现这两阶振型及固有频率近似，同样为重根模态，振型趋势都为在XOZ平面进行双节点摆动。

由于主轴回转方向未设置弹簧刚度，故其第一阶表现为自由回转，且设置的弹簧刚度在轴向比径向大，所以第二、三阶振型趋势首先表现在径向方向的移动，频率接近。此外，主轴转子结构基本为回转对称类结构，因此容易出现重根模态的情况，然后再表现为第四阶轴向的整体移动。前四阶主轴转子基本为整体刚性位移，主轴转子本身未发生变形，为刚性模态。这是因为气膜处设置的弹簧刚度小于主轴材料本身刚度，因此前四阶振型首先发生在刚度较为薄弱的弹簧连接处，从第五阶起主轴转子开始变形，出现弹性模态的情况。

在不考虑一阶自由刚性模态和重根模态的影响下，主轴转子的模态可以认为第一阶为2、3阶的平均值278 Hz、第二阶为316 Hz、第三阶为5、6阶的平均值384.5 Hz。

2.2.2 主轴部件含所有零部件的仿真结果

以整体外壳支架为支撑体，主轴部件的前六阶振型趋势及模态参数信息如图8及表3所示。

图8 主轴部件前六阶模态振型趋势

上述结果表明，外壳对于主轴转子的模态有一定影响，首先主轴部件不再是严格的对称结构，因此重根模态的情况减弱甚至消除，主轴部件内部刚度不变，质量增加引起各阶固有频率呈现下降的趋势，同时外壳在每阶的振型趋势会影响主轴转子的振型，主要表现为外壳振型的变形趋势会叠加到主轴转子上，例如表3中第二阶模态参数所示，主轴部件在Y移动方向上参与系数为0.9，参与的有效质量为0.25，同时在Z移动方向上参与系数为1，参与的有效质量为0.15，相较于2.2.1节中第二阶的振型趋势，主轴部件不仅在沿着Z方向移动，还有一部分质量的外壳部分沿着Y移动，外壳部分结构沿着Y方向移动的同时带动主轴转子在Y方向移动，虽然此时在X移动方向的参与系数为0.24，但是参与的有效质量为0.02，所以沿着X方向的移动可以忽略。由此可以发现，主轴部件基本振型趋势与2.2.1节中的主轴转子振型趋势一致，但是在原有主轴转子的基础上同时叠加了主轴外壳等其他部件的振型。

表3 主轴部件仿真结果模态参数

3 模态试验

3.1 试验测试基本理论

对于多自由度系统而言，系统在拉氏域所表示的传递函数为[11]

其中：B(s)=Ms2+Cs+K，B(s) 为关于质量矩阵M、阻尼矩阵C、刚度矩阵K的系统矩阵；A(s)为留数矩阵，留数矩阵包含系统模态振型信息；det[B(s)]为特征方程，特征方程的解为系统传递函数的极点，极点与系统固有频率有关。特征方程det[B(s)]的第n阶根Pn为[12-13]

实部 σn为系统阻尼比与无阻尼固有频率的乘积，虚部 ωdn为系统有阻尼固有频率。H(s)是系统响应与激励之比，表现为一个复数值的曲面。系统频响函数是系统传递函数曲面在s=jω轴上的一条切线。假设系统为一个具有m自由度的系统，令s=jω，以复数共轭形式特征根Pn表示的部分分式形式的频响函数为[14]

当在系统中布局多个激励点及响应点时，对于在特定点（系统在i处响应，在j处激励）的频响函数为[14]

在特定点（第i处响应，第j处激励）的频响函数展开为

由以上公式可以看出，当在系统中任意一点进行激励、响应测量时，系统的频响函数都会得到P1到Pn的值，即为系统从第一阶到第k阶的系统固有频率信息。aij1至aijn则显示了系统关于本测量点处从第一阶到第k阶的模态振型信息。当改变激励及响应位置时，频响函数的极点信息不变，固有频率也不变，但是留数矩阵会发生变化。这意味着理论上对一个系统进行模态测试时，只需要测量一个激励点及响应点的频响函数即可获得系统全部固有频率信息，但是振型信息仅仅是获取的关于此特殊位置的变形。当激励位置或响应位置发生变化时，振型也会发生变化，因此当采用锤击法进行模态测试时，应布局多个传感器的响应位置以获取更全面的模态振型信息，或者说应至少获取多个参考点组成的频响函数矩阵中的其中一行才可以较为完整的描述系统模态振型[15]。为最大程度避免可能出现的“丢阶”现象[16]，锤击激励位置也应选择多个点进行锤击，即本次模态测试采用MIMO测量方法[17]。

3.2 软件设置及方案

根据第2节有限元分析结果，主轴结构前六阶最高频率为385 Hz，依据香农定理[18]：

此次重点分析的频率上限fmax至少为400 Hz。因有限元仿真前六阶中包含重根模态频率，为避免漏失模态，结合软件设置情况现将频率上限fmax设定为1 024 Hz，采样频率fs为2 046 Hz，谱线数M定义为1 024，频率分辨率 Δf为1 Hz。

测试设备采用LMS振动测试仪，测试方式采用移动力锤固定传感器的形式，软件针对频响函数噪声的处理采用HV估计方式，传感器采用单向加速度传感器。为分别观察主轴转子、轴瓦、整机外壳及电机部件对模态结果的响应，共计布置14个传感器。同时为保证有效测量主轴整机的各阶模态固有品频率参数，避免因激励点选取不当引起的无法激励全模态信息的情况，在对应传感器的相同或对立方向进行激励。其中传感器及激励点的具体位置及方向如图9及表4所示。试验测试设备及传感器布局现场如图10所示。

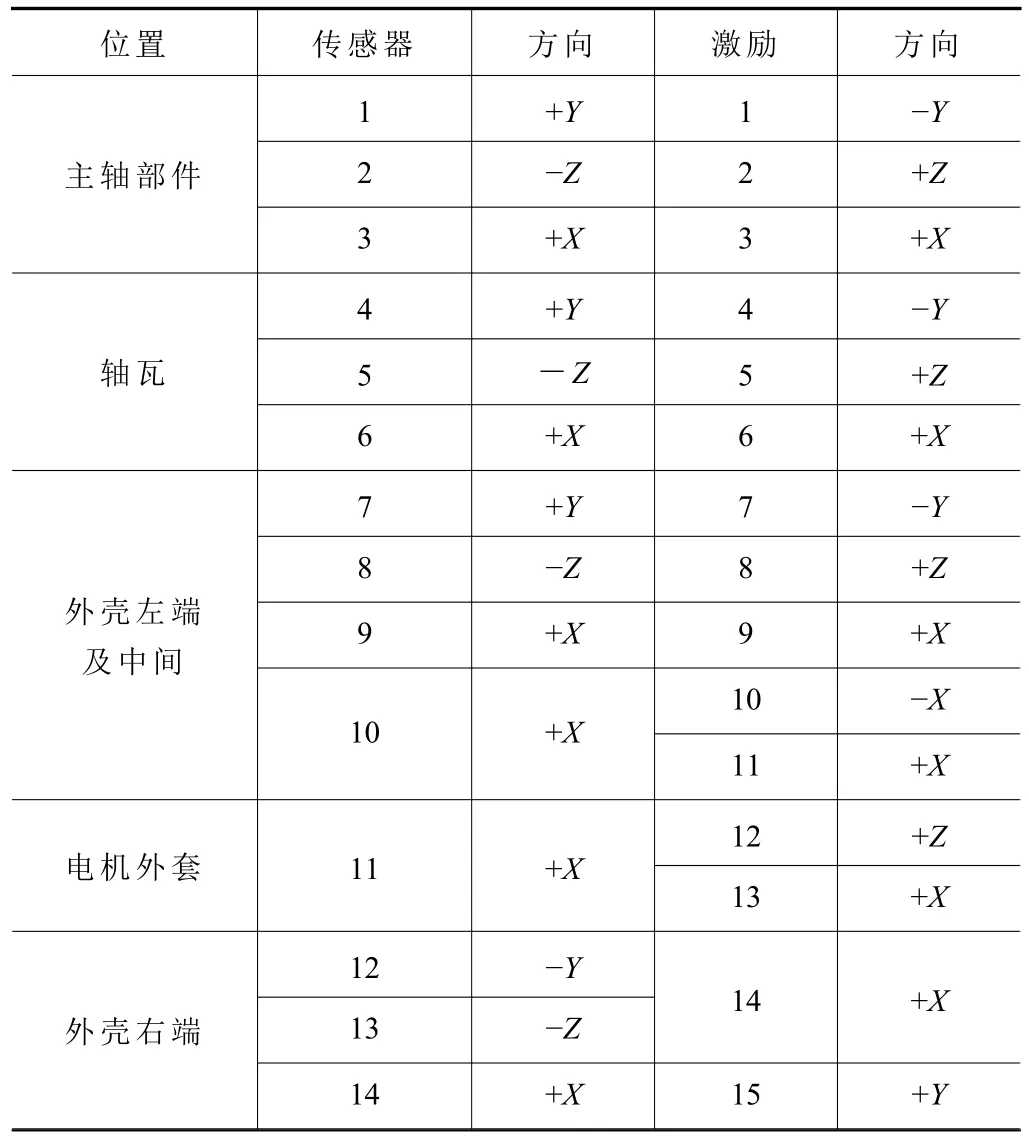
表4 传感器及激励点的位置与方向分布表

图9 主轴装配体传感器位置布置图

3.3 测试结果分析

在对所有结果进行筛选时，频响函数的质量可以利用相干函数来进行评估，其相干函数的定义为[19]

其中：Gyx、Gxy为输入输出的互功率谱，Gxx为输入自功率谱，Gyy为输出自功率谱。自功率谱为标量值，互功率谱为复数值，相干函数的取值范围为0～1。相干数值越趋近于1，表明所输出的响应信号与输入的激励信号相关性越高，代表频响函数的可靠性越高。此次试验参考点位置共14个，激励点位置共15个，共分别210个相干曲线及频响函数。为节约时间，在确保主轴整机不同部件及位置处均能保留至少一个激励点的前提下，通过对相干函数的检查，从所有结果中选出相对质量较好的激励点，最终确定保留的激励点为3、6、11、13、14。针对保留的激励点进一步选择每个激励点中所有参考点中质量较好的相干函数，最终保留的激励点及参考点相干函数质量如图10所示。激励点3和激励点6的相干函数相较于激励点11、13、14波动较为严重，且分别在250 Hz和500 Hz以后出现急剧下降，因此进一步选择激励点11、13、14的频响函数结果获取系统极点信息。激励点11、13、14的相干函数在550 Hz以前基本保持为1且曲线较为平直，说明输入与输出之间存在较好的关联，在550 Hz以后也开始出现曲线下降及紊乱波动的情况，因此在分析激励点对应的频响函数时，550 Hz以内的结果是比较可靠的。各激励点的相干质量曲线如图11所示。

图10 现场测试试验

图11 保留的激励点及对应参考点的相干质量曲线

对最终选择的激励点11、13、14进行频响函数的模态参数估计。参数识别方法采用复模态指示函数CMIF及PolyMAX稳态图综合的方式进行选取，当同时出现复模态指示函数峰值、频响函数峰值且极点位置为S列时，则认为是系统其中的一阶模态。按照以上原则分别对激励点11、13、14的频响函数曲线进行各阶模态参数的选取，如图12～14所示。

图12 激励点11对应的频响函数曲线

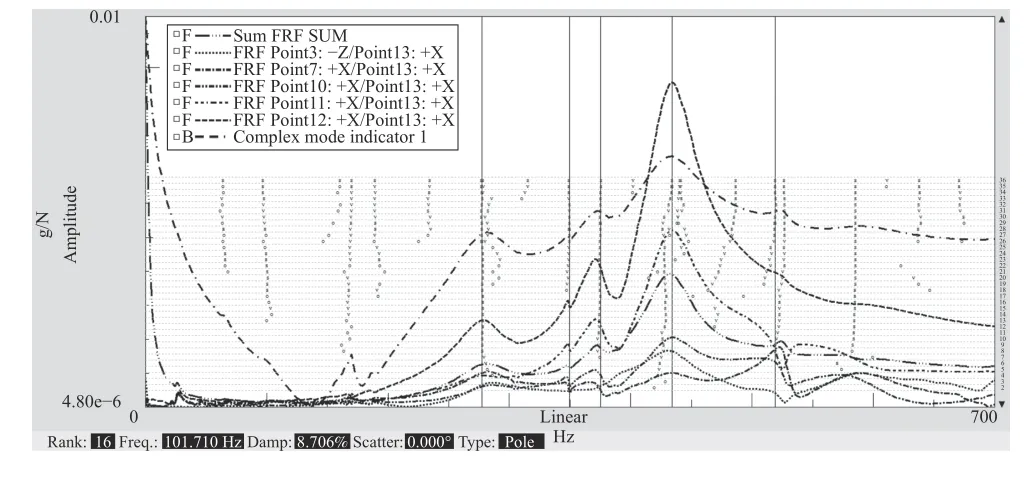
图13 激励点13对应的频响函数曲线

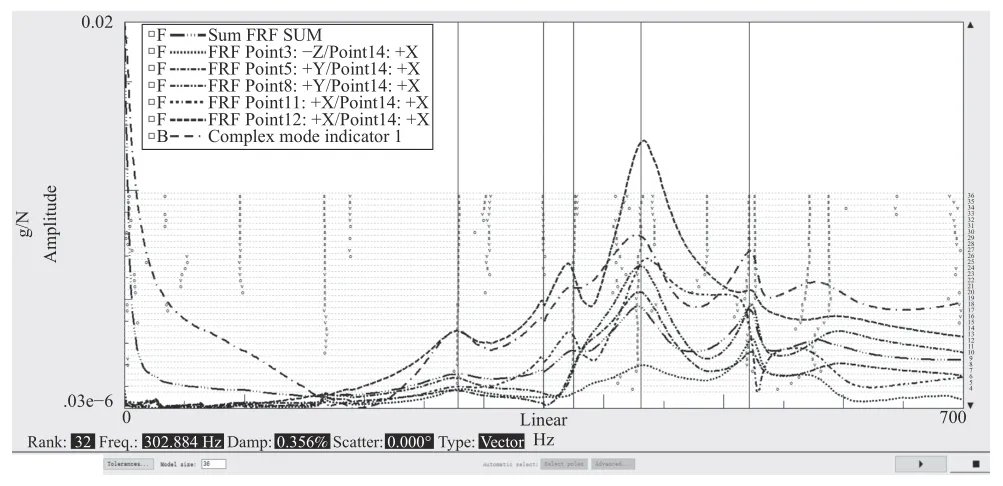
图14 激励点14对应的频响函数曲线

为避免快速傅里叶变换过程中的信号泄露问题，测量过程中针对激励输入信号及响应输出信号分别添加了力-指数窗及指数窗，由此造成了响应峰值减弱。同时，主轴部件与轴瓦之间利用气膜约束的方式存在较大阻尼，系统在极点位置处频响函数的峰值表现得较为平宽，因此试验并没有很好地识别出频率极为接近的重根模态。通过测试试验得到的主轴部件各阶固有频率与有限元仿真结果的对比如表5所示。

表5 仿真与试验结果对比

4 结语

4.1 结论

通过主轴转子和主轴部件的有限元仿真分析，获取了不同结构的两个有限元模型固有频率，同时采用锤击法对主轴部件进行模态试验验证。通过仿真分析及试验验证得出以下结论：

（1）不考虑自由刚体模态及重根模态的情况下，主轴转子结构模型的前三阶固有频率为277 Hz、316 Hz和384 Hz，主轴部件结构模型的前三阶固有频率为259 Hz、281 Hz和352 Hz。主轴部件结构模型的质量增加和不对称性会导致整体固有频率呈现下降的趋势，且存在重根模态情况但是有所减弱。

（2）试验测试结果表明前三阶固有频率平均值分别为276.3 Hz、349.6 Hz和374.4 Hz，与主轴转子结构模型的有限元频率结果误差为0.6%、10.6%和2.6%，与主轴部件的有限元频率结果误差为4.5%、24.4%和4.7%。主轴部件的测试结果与仿真结果误差相对更大，此问题产生的原因可能为：试验测试过程中外壳通过螺栓安装固定在试验台上且为通气状态，受其试验台限制，外界力能够更好地激励主轴转子部分，因此参与模态响应的实际质量多集中于主轴转子部分，且整体参与的有效质量小于主轴部件质量，导致试验数据结果偏高，具体原因需要尝试更多不同边界条件下的试验进行进一步验证。

4.2 建议

（1）进行主轴部件模态试验时，考虑安装位置及附加质量的影响，可以进行主轴部件自由边界条件下的测试。主轴转子与轴瓦之间的支撑方式为气膜介质，主轴转子与外壳没有实际接触，零部件之间激励信号传递不佳，可能导致无法有效激励起所关心带宽内的所有模态，需要进一步考察气体静压主轴中气膜的存在对模态参数响应的影响。

（2）试验过程中若采集到的时域信号及响应信号能够自然衰减至零，可以不用加窗，避免由于降低响应信号幅值导致模态指示函数或频响函数无法有效识别出重根模态。