基于BP神经网络的矿车运行时矿井摩擦阻力的预测*

冯 燕，刘 剑

（1.辽宁工程技术大学安全科学与工程学院，辽宁 葫芦岛 125105；2.辽宁工程技术大学矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105）

0 引言

近年来，矿山机械化程度在逐渐提高的同时，矿井生产能力也在日益增长，矿井活塞风效应问题依然是目前研究的重点。井下运输设备在运行工作时，风流受到巷道壁面的限制，其速度或方向在绕过障碍物时发生变化，使得风流本身出现急剧反应，形成的涡流较为紊乱，此时矿井摩擦阻力变化较大，活塞效应明显，影响预期通风效果。

目前，活塞风效应不仅在公路、隧道、地铁等工程中研究较多，在矿井通风方面也取得较大突破。王从陆等[1-2]运用Fluent模拟软件分析矿内运输工具运行时巷道的空气流场分布和压力分布情况；邬长福等[3]采用动网格技术通过控制变量研究不同因素对巷道气流组织影响的变化规律；王海桥等[4]运用计算流体力学软件分析研究罐笼运行时井筒内的流场和压力场的变化情况；彭云等[5-6]从装载程度和矿车运行状态2 个方面对巷道风流场进行模拟计算研究；张宏杰等[7]从数值模拟与现场实测的角度对井下防爆胶轮车运行时巷道通风阻力的变化情况进行分析研究；王文才等[8-10]不仅对Y形巷道进行速度及压力变化情况的分析，而且进一步研究分析矿井提升设备在运行过程中产生的活塞效应对立井风流的扰动规律。

目前，多数人用CFD软件对其进行模拟分析，但在涉及其建立模型、网格划分、设置边界条件、迭代运算等步骤时，有可能会面临计算量较大的问题，影响结果的准确性。因此，在矿井通风过程中，准确地预测出矿车等运输设备运行时巷道摩擦阻力的变化情况是非常重要的。在井下矿车运行时，影响巷道摩擦阻力变化的因素有巷道风流速度、阻塞比、矿车运行速度、矿车长度、巷道总长度、巷道宽度、风向等。本文将重点结合动网格技术研究矿车运行时巷道摩擦阻力的变化情况，从巷道风流速度、矿车运行速度、阻塞比、矿车长度4 个矿车运行时对巷道摩擦阻力产生影响的因素作为切入点，依据模拟得到的巷道摩擦阻力数据建立相应的BP神经网络模型进行训练与学习，进而对矿车运行时矿井的摩擦阻力变化情况做出准确预测。

1 BP神经网络的基本原理

BP神经网络是1 种采用梯度下降法的多层前馈网络，其重点就是实现误差的反向传播训练。网络学习训练有正反2 个传播过程。从正向传播过程来看，隐含层接收到输入信号后通过相应的传递函数作用于下一级，经过一系列变换产生所需要的输出信号，以期望值为准，所得结果与之相差较大时，误差将以相反的方向进行传播。反向传播就是将误差通过隐含层逆向传到输入层，从而达到不断更新各单元权值的目的[11-13]。随着神经网络的学习训练，权值也一直在持续的迭代更新。3 层网络结构如图1所示，其中[X1，X2，…，Xm]为输入样本，[Y1，Y2，…，Yn]为输出样本。

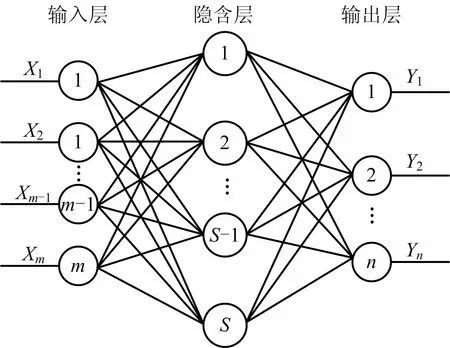
图1 3 层BP神经网络结构Fig.1 Structure of three-layer BP neural network

隐含层各单元的输出如式（1）所示：

式中：θj为神经元阈值；f为非线性函数；Wij为隐含层的权值矩阵；Xi为输入样本值，i=1，2，…，m；Oj为隐含层输出结果，j=1，2，…，S。

输出层的输出结果如式（2）所示：

式中：θk为神经元阈值；f为非线性函数；Wjk为输出层的权值矩阵；Yk为输出层输出结果，k=1，2，…，n。

将网络预测输出值与期望值进行比较，确定误差函数ek。并根据该误差，结合公式来不断更新网络权值，在误差收敛至期望值时结束训练。其公式如式（3）～（4）所示：

式中：η为学习速率；ek为误差函数；i=1，2，…，m；j=1，2，…，S；k=1，2，…，n。

2 基于CFD数值模拟的训练样本

2.1 主控制方程

矿车等运输设备在巷道内运行产生的活塞效应是导致巷道风流状态发生变化的重要因素。为了方便计算，现做出以下假设：1）矿井风流流动属于不可压缩流动；2）入口风流处于稳定状态，满足Boussinesq 假设；3）巷道壁面绝热恒温，忽略风流与巷道壁面摩擦产生的热量；4）仅考虑列车单侧行驶，不考虑矿车相向而行；5）矿车在巷道内作匀速运动。由于将流体视为不可压缩流动，所以紊流模型选择标准k-ε方程模型。其中，连续方程如式（5）所示：

式中：ui为流体水平方向上的速度分量，m/s；xi为流体水平方向上的速度分量。动量方程如式（6）所示：

式中：fi为质量力，m/s2；t为时间，s；γ为系数；Pk为修正时均压力，Pa；xi，xj分别为流体水平和垂直方向上的坐标分量；ui，uj分别为水平和垂直方向上的速度分量，m/s。

k方程如式（7）所示：

式中：vt为紊流黏性系数，vt=Cuk2/ε；υ为动力黏性系数，Pa·s；Gk为紊动能产生项，；k为紊流动能，m2/s2；ε为紊流动能耗散率，m2/s3。

ε方程如式（8）所示：

式中：模型中的常数的取值为C1ε=1.44，C2ε=1.92，Cu=0.09，σk=1.0，σε=1.33。

2.2 物理模型

为了快速有效地预测矿车运行时矿井摩擦阻力的变化情况，本文选择采用动网格技术模拟矿车运行，因此，结合矿井巷道和矿车的实际尺寸，将研究对象简化为一段长为50 m的巷道，断面为半圆拱形，宽3 m，巷高1.2 m，支护方式为锚喷支护，多节矿车简化为长方体，断面为矩形，高为1.6 m，长度和宽度根据模拟需要分别取不同的值，为了方便计算，建立巷道内矿车运行的二维模型如图2所示。其矿车和巷道均简化为矩形，几何模型相关参数如表1所示。其中巷道阻塞比是由矿车断面积/巷道断面积而来。

图2 巷道内矿车运行几何模型Fig.2 Geometric model of tramcar running in roadway

表1 几何模型相关参数Table 1 Related parameters of geometric model

2.3 边界条件及求解器设置

利用前置模型处理软件Gambit，根据各方案需要，建立相应尺寸的二维几何模型，经过布尔运算，以0.08 mm为单位，对模型进行网格划分，巷道内矿车运行几何模型如图2所示。选择巷道左侧风流入口为速度入口，巷道右侧风流出口为自由出流。巷道壁面默认roughness constant为0.5。由α=可知，影响摩擦阻力系数的因素主要为沿程阻力系数λ与空气密度ρ，而本次模拟在密度一定的情况下，通过不断调试计算，与经验值进行比较，得出锚喷支护巷道在Fluent中粗糙高度应设置为0.05 m。同样的，设置矿车表面粗糙高度为0.01 m。

将矿车运动设置为刚性运动（rigid body），通过导入相应的profile文件来控制矿车的运行速度，选择弹簧光顺和网格重构2 种方法，前者设定弹簧因子为0.6，后者设定最小合并尺寸为0.05 mm，最大分裂尺寸为0.1 mm，其余参数默认即可。

模拟过程中采用压力隐式分离的求解器，速度选择绝对速度，湍流模型选择标准k-ε双方程模型，流场求解计算方法选择Simple算法。

3 构建矿井摩擦阻力预测模型

3.1 样本的获取

通过改变巷道风流的速度，矿车的运行速度，阻塞比及矿车的长度这4 个因素，对巷道的摩擦阻力进行模拟，通过控制变量选取Fluent模拟得出的90 组数据作为训练和测试样本，部分数据如表2所示。以预测矿车运行时矿井的摩擦阻力为目标，利用BP神经网络算法构建巷道摩擦阻力预测模型，预测模型以矿车运行影响因素作为输入层，以巷道摩擦阻力作为输出层。

表2 BP神经网络学习和检验样本Table 2 Learning and test samples of BP neural network

3.2 网络模型的学习训练

在人工神经网络的应用中，BP神经网络拥有自适应性、自学习性、自组织记忆等强大的非线性表达能力。以上述样本数据为准，构建基于BP神经网络的矿车运行时矿井摩擦阻力的预测模型。其巷道摩擦阻力网络模型如图3所示。

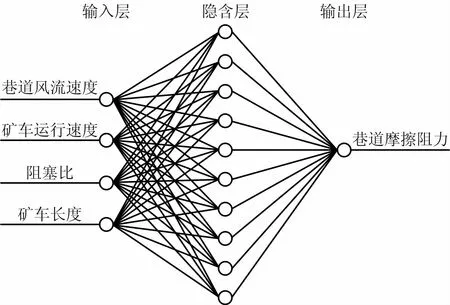
图3 巷道摩擦阻力网络模型Fig 3 Network model of roadway friction resistance

1）网络评价指标

选用相对误差ε对模型的性能进行评估，其计算公式如式（9）所示：

式中：y1为BP神经网络预测值（下文简称预测值）；y为Fluent模拟值（下文简称模拟值）。

2）激励函数选择

依据BP算法，选择对数S 型正切函数（tansig）为输入层与隐含层间的映射函数，线性传递函数（purelin）为隐含层与输出层之间的映射函数，训练函数选择trainlm[14]。其中对数S 型正切函数表达式如式（10）所示：

线性传递函数如式（11）所示：

3）其他参数设置

期望误差的最小值设为0.000 5，训练步长设为1 000；学习率设为0.03。

4）隐含层神经元个数的确定

有研究发现，影响网络模型预测精度的主要因素有输入节点数和隐含层节点数。对于隐含层来说，节点数过少时，网络训练不够，映射关系简单，欠拟合现象明显；节点数过多时，训练过度，时间明显增加，过拟合现象出现频繁。在实际构建中，一般通过经验公式运用“试凑法”确定其具体节点数[15]。本文使用的经验公式如式（12）所示：

式中：m为输入层节点数；n 为输出层节点数；S 为隐含层节点数；a 为常数，一般取值范围为1～10。

由上文可知，m=4，n =1，代入式（12）得S ∈[4，13]，S∈N+。经网络测试，确定隐含层节点数为10 时，模型效果最为理想。

4 模型预测结果及其检验

4.1 模型训练结果

基于上述参数设置的基础上，对矿车运行时矿井摩擦阻力的预测模型进行训练，训练相关情况如图4所示。

由图4（a）可知，神经网络模型在训练时，随着训练次数的增大，训练误差在逐渐下降，直到达到期望误差，逐渐收敛。而由图4（b）可知，训练集和测试集的全部拟合度为0.966 5，R值越接近1，预测值越准确，说明所建立的神经网络性能越好，因此，该网络模型可以较准确预测矿车在巷道内运行时矿井摩擦阻力变化情况。

图4 巷道摩擦阻力模型的训练情况Fig.4 Training of roadway friction resistance model

4.2 模型检验

选取表2中序号为86～90 的样本数据作为此神经网络的测试样本，通过对比预测结果与模拟结果来评估其网络性能的好坏，网络预测值与模拟值结果对比如表3所示。

表3 网络预测值与模拟值结果对比Table 3 Comparison between network predicted values and simulated values

根据计算结果分析可知：将神经网络预测所得的巷道摩擦阻力与模拟值相比较，最大绝对误差为3.069 002 1 Pa，最大相对误差为6.051%，充分说明该神经网络模型能够满足预测要求，能够快速有效地确定矿车等运输设备运行时巷道的摩擦阻力变化情况，误差较小，具有一定的应用价值。

4.3 应用实例

为了说明基于BP神经网络的矿车运行时矿井摩擦阻力预测具有普适性和工程应用价值，在实验室的实验巷道内进行矿车运行时巷道摩擦阻力的实测工作，实验巷道长86 m，断面尺寸为3 m×2.5 m（宽×高），断面形状为矩形，支护类型为工字钢支护，实验矿车尺寸为2.4 m×1.3 m×1.6 m（长×宽×高）。选取1 段风流较稳定的巷道，在其两端布置风压采集装置，作为监测点，测量矿车不同速度运行下巷道的摩擦阻力，得出相关数据，并采用该神经网络进行训练，实验巷道的实测值与预测值结果对比如表4所示。

表4 实验巷道的实测值与预测值结果对比Table 4 Comparison between predicted values and actual measur ed values of experimental roadway

通过对比发现，预测值与实测值比较接近，最大相对误差为2.12%，预测结果误差范围在3%以内，其预测模型用于实际求解矿车运行时矿井摩擦阻力的变化情况是可行的，能满足实际需要。

5 结论

1）利用CFD软件模拟获得的巷道摩擦阻力数据，可以作为构建神经网络的数据基础，并且具有较好的普适性。

2）将BP神经网络预测的巷道摩擦阻力结果不论是与Fluent模拟结果对比，还是与实测结果对比，预测结果相对误差范围在7%以内，将该神经网络模型，用于实际求解矿车运行时巷道摩擦阻力的变化情况具有良好的适用性和可行性，有一定的实用价值。