例谈立体几何探究问题中的引参法
2023-02-24苗兴振
苗兴振
(山东省淄博市沂源县第二中学)
立体几何中的探究问题在高考和各类模拟考试中经常出现,这类题型有助于考查学生推理能力、探索能力和批判性思维能力,也有利于培养学生的空间想象能力、创新意识和综合素质,具有一定的区分度,深受命题者的青睐.探究性问题常常涉及平行、垂直、距离和夹角等常考不衰的重点内容,常以解答题的形式出现.这类问题的一个共同特点是要确定动点的位置使得问题具有某种数量关系或位置关系等属性,而解决这类问题的难点和关键最后都归结为如何确定动点的位置.若用向量法处理,尤其是通过建立空间直角坐标系利用待定系数法求解存在性问题则思路简洁明了.下面我们通过典型例题解读立体几何探究问题中的引参法,供读者参考.
1 与平行、垂直有关的问题
平行与垂直是立体几何的两种重要的位置关系,其中线线的平行与垂直是基础,线面平行和垂直是重点考查内容,应引起高度关注.
例1如图1所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
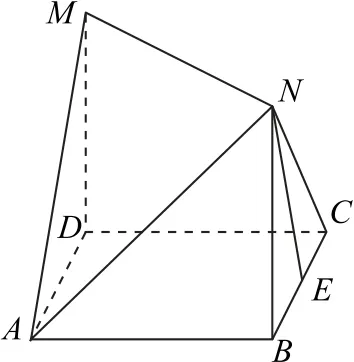
图1
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN? 若存在,求线段AS的长;若不存在,请说明理由.
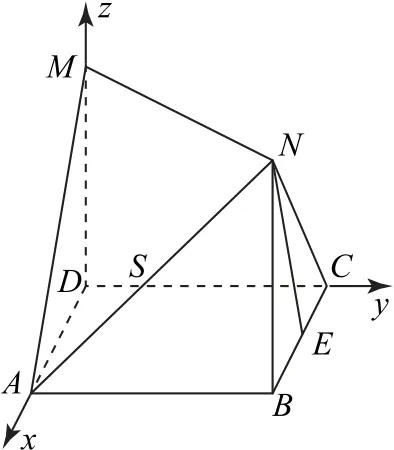
图2
所以异面直线NE与AM所成角的余弦值为
(2)假设在线段AN上存在点S,使得ES⊥平面AMN.连接AE,SE,如图3所示.
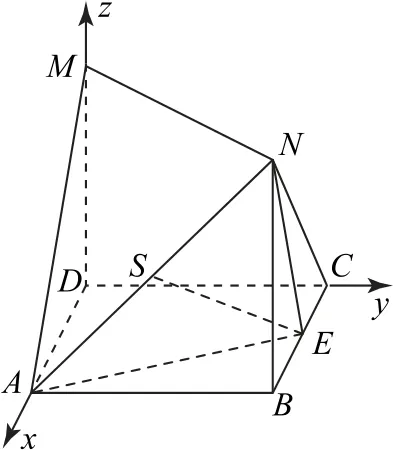
图3
2 与夹角有关的问题
夹角问题主要有线线角、线面角和面面角,其中线线角是基础,线面角和面面角是高考重点考查内容.
例2如图4所示,在四棱锥P-ABCD中,侧面PAB⊥ 底面ABCD,底面ABCD是直角梯形,AD∥BC,BC⊥AB,∠PAB=120°,PA=AD=AB=1,BC=2.
图4
(1)证明:平面PBC⊥平面PAB;
(2)在线段PB上是否存在点M,使得直线AM与平面PBD所成角的正弦值为.若存在,求出线段PM的长度;若不存在,请说明理由.
(2)存在.理由如下:如图5 所示,在平面PAB内,过点A作AE⊥AB交PB于 点E,则AE⊥平面ABCD,以A为坐标原点,分别以AB,AD,AE的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系A-xyz.
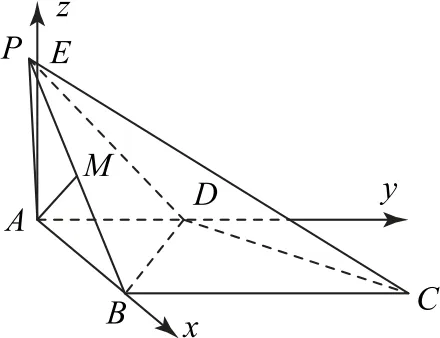
图5
3 与距离有关的问题
空间中的距离问题主要有点点距离、点线距离、点面距离、线线距离、线面距离和面面距离等,其中点面距离是高考重点考查内容.
例3如图6 所示,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,CA=2,D是CC1的 中点,试问在线段A1B上是否存在一点E使得点A1到平面AED的距离为.若存在,试确定点E的位置;若不存在,请说明理由.
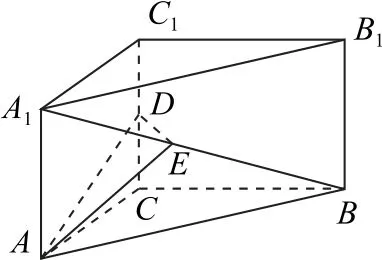
图6
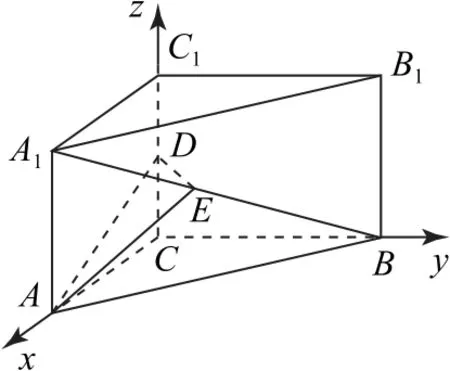
图7
故存在满足条件的点E,且这样的点E有两个,一个是线段A1B的中点,另一个就是点B.
4 变式练习
变式如图8 所示,已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
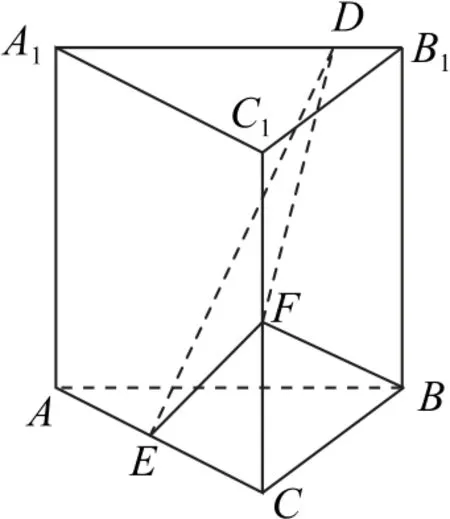
图8
(1)证明:BF⊥DE;
(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?
如图9 所示,连接AF,由BF⊥A1B1,AB∥A1B1,得BF⊥AB,于 是,故由AB2+BC2=AC2,得BA⊥BC,故以B为坐标原点,以BA,BC,BB1所在直线分别为x轴、y轴、z轴建立如图9所示的空间直角坐标系B-xyz,则B(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(1,1,0),F(0,2,
图9
设B1D=m(0≤m≤2),则D(m,0,2),于是,所以,故BF⊥DE.
(2)易知平面BB1C1C的一个法向量为n1=(1,0,0),设平面DFE的一个法向量为n2=(x,y,z),则
令x=3,得y=m+1,z=2-m,于是平面DFE的一个法向量为n2=(3,m+1,2-m),所以
当所确定的点在某条直线上运动时,通过建立空间直角坐标系,利用向量平行(共线)的充要条件,通过引入参数λ建立两个向量的等式,从而用向量的坐标运算确定点的位置.这种确定点的位置的方法称之为“引参法”,其理论依据是共线向量定理:非零向量a,b共线的充要条件是存在唯一的实数λ,使得b=λa.
立体几何中探究问题的解决除了本文所用的方法外,还可用猜测探求、执果索因、假定探索等方法,限于篇幅,这里就不赘述了.
(完)
