基于水力-热力耦合模型的供热管网优化调度研究

李 鸿，张 欢，王雅然，米雷洋，史凯雨，由世俊

基于水力-热力耦合模型的供热管网优化调度研究

李 鸿1, 2，张 欢1，王雅然1，米雷洋2，史凯雨3，由世俊1

(1. 天津大学环境科学与工程学院，天津 300350；2. 天津市城市规划设计研究总院有限公司，天津 300190；3. 浙江大学建筑设计研究院有限公司，杭州 310028)

在城市集中供热管网运行过程中，供热系统的输配能耗由水泵能耗和供、回水管网的热损组成，降低供热系统的输配能耗对实现低碳供热目标具有重要意义．本文基于网络图论、流体输配原理和管道的一维传热，建立了集中供热管网的动态水力-热力耦合模型，并针对天津市实际供热管网的运行过程进行了仿真模拟，利用实际运行数据验证了动态水力-热力耦合模型的精确性．建立了集中供热管网输配能耗的计算模型，并对供热系统的运行能耗进行经济性分析．基于所建立的能耗分析模型，结合粒子群优化算法，建立了多热源环状管网的优化调度方法，该方法以供热管网的总输配损耗的成本最低为目标函数，以热源的供水温度、热源泵的转速比、热力站入口处的阀门开度为决策变量，以满足能量守恒和质量守恒为约束条件，通过进行算法参数匹配，给出基于PSO算法的多热源环状供热管网优化调度的计算步骤，并结合天津市实际管网对优化调度方法的调控过程进行了分析．仿真计算结果表明，由于管网存在输配延迟属性，热力站的总负荷变化与室外温度变化不存在静态的正相关性，此外，也发现水泵运行费用为整个管网运行费用的主要组成部分，占总运行费用的58%以上．本研究为城市集中供热管网运行调节的优化提供了一套有效的计算工具．

集中供热管网；粒子群优化算法；运行调节；能耗分析；动态水力-热力耦合模型

在城市大型集中供热管网系统中，末端用户的供热效果受一级供热管网的流量大小和供水温度的影响较大．各个热力站处的供水温度和供水流量与供热管网系统在运行调节时的水力工况和热力工况息息相关．而且，供热管网中的水力工况和热力工况也相互联系相互影响．热源将管网中的介质通过水泵输送到各个热用户，管网各处的流量分布情况影响着介质温度和热量分布；同时，各个用户热力站处的供回水温度的变化对供热系统水力工况的调节进行持续地反馈以保障整个供热系统的平稳可靠运行．

供热系统运行调节中的能耗受水力、热力两类工况耦合特性的影响较大，为了进一步提高供热系统效率，对管网水力-热力耦合建模与分析不可或缺，且随着大型多热源环状管网完善与运行，管网的水力工况和热力工况更加复杂．在满足各个热用户用热需求的前提下，保障供热系统平稳安全运行、最大化减小管网的运行能耗、降低供热系统的运行费用是亟待解决的管网优化调度问题．

Oppelt等[1]基于拉格朗日法对集中供冷管网建立了准静态水力模型和动态热力模型，并将该耦合模型应用于实际工程进行验证分析，所建立的水力-热力耦合模型能够达到较好的数值精度，对枝状管网的运行调节具有一定的参考价值．Liu等[2]建立了一套水力-热力耦合模型用于分析集中供热管网，在该模型中，热力模型的求解主要取决于水力部分计算结果，且根据获得的热力工况仿真结果，水力模型参数得以不断更新，从而使得水力部分也可迭代进行．该方法采用稳态的热力模型来描述管网热水温度的分布特性，对管网的热动态特性的适应性较低．Wang等[3]提供了水力-热力耦合计算流程，在计算过程中采用稳态的水力模型以及动态热力模型来描述管网中热水流量和温度的分布特性，采用显式数值格式进行求解．王庆峰[4]针对采用质量并调的集中供热系统，以最小化系统运行费用为目标函数，结合供热管网的运行特性，得到供热系统一次网运行优化数学描述，并开发了一套软件系统，用于在不同阶段选取合适的方法求解该优化问题．周守军[5]针对采用质量并调运行策略的集中供热管网，以最小化系统运行成本为目标函数，根据管网输配特性和实际工程要求建立约束条件，并采用非线性规划对优化问题进行求解. 时国华等[6]研究了多热源集中供热系统的运行特性，并在此基础上构建了供热系统多目标优化调度模型，其中目标函数为系统的经济性和环保性，并以热负荷供需平衡、流量守恒以及热源的运行状态为约束条件，通过求解该优化问题，可以确定实际运行过程中各热源的最佳运行状态及其负荷．

本文通过建立大型环状集中供热管网的水力-热力耦合模型，结合供热管网系统的能耗模型，通过融入粒子群算法进行大型供热管网优化调度方案研究，给出计算模型和计算方法，进一步为实际的大型供热管网的运行调节提供参考．

1 供热管网的水力-热力耦合模型

在城市大型多热源集中供热管网系统中，压力波动的传播速度远远大于温度波动的传播速度，压力波传动速度约有1000m/s[7]．故在进行水力-热力耦合模型的建立和求解过程中，通常先对管网的水力模型进行求解，再将计算结果与建立的热力模型进行结合，最后计算最终解[8]．

1.1 管网的稳态水力模型

对于城市集中供热管网，可以利用图论和矩阵理论对管网进行数学描述[9-11]．

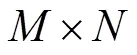
管网的基本关联矩阵可写为

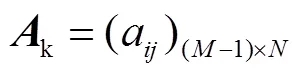
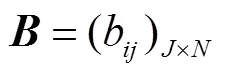
根据相关矩阵知识，管网的独立回路矩阵可写为

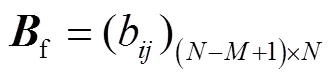
且有[12]

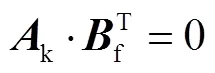
根据基尔霍夫第一和第二定律，可以建立管网的质量守恒和能量守恒方程，有

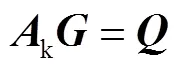
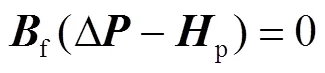
联立式(6)和式(7)，根据集中供热管网的拓扑结构以及热力站的流量信息，可利用迭代法对管网的水力模型进行求解[13]．

1.2 供热管网的热动态模型

对于实际工程而言，可将供热系统中的热水视为不可压缩流体，且在管网中热水的温度在一定范围内变化，故将热水的密度和导热率视为常数．与热水在管网中的对流换热相比，热水沿管长方向的导热远小于热对流，故可忽略沿径向温度的变化及沿管长方向的导热．基于以上假设，单根热水供热管道中沿管长方向的温度场可以表示为

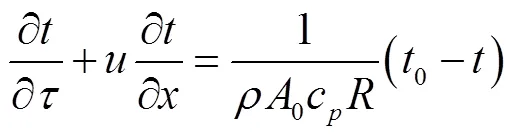
在热水供热管网中，管道的散热损失可以分为4部分：热水和管壁间的对流换热热阻，管壁、保温层以及土壤导热热阻[14-15]．与前两项热损失相比，管道保温层的热阻和土壤导热热阻占比很大，故在本文的研究中忽略管壁导热热阻、热水和管壁间的对流换热热阻．热水管道的总热阻计算式为

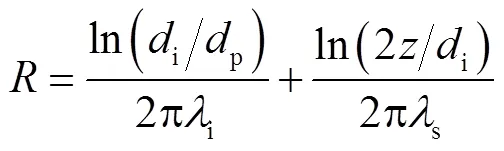
在对热水管道进行热力模型的创建之后，可根据有限体积法对供热管道划分控制体并通过隐式迎风差分格式对控制体进行差分求解[16-17]．

如图1所示，将单根管道划分为若干个控制体，假定每个控制体沿管长方向的温度分布均匀．

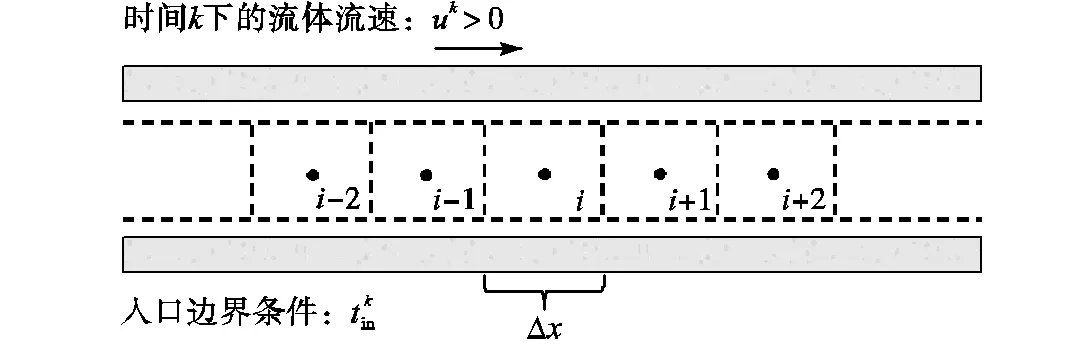
图1 供热管道控制体划分

对于式(8)中的对流项和非稳态项，采用隐式迎风差分格式进行差分，考虑热水在管道中进行输送时流动方向的改变，控制体的表面温度与上游控制体的温度相关[18-20]．

对于控制体，其对流项可表示为

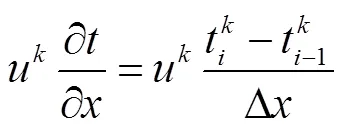
由式(8)和式(10)，可得

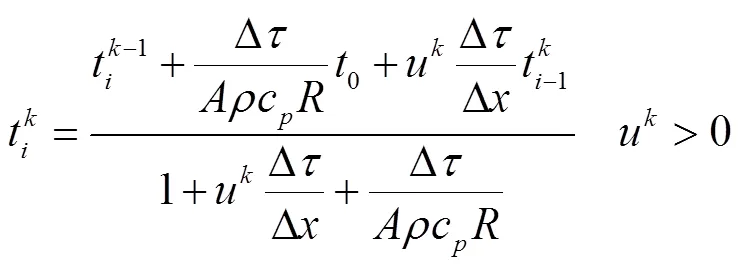
对于环状管网，流体流动方向会发生变化，相应的表达式为

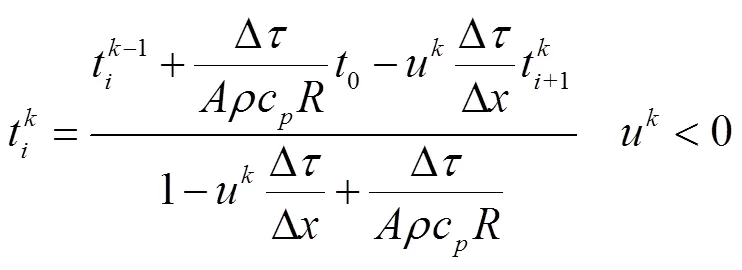
在对对流项进行离散时，隐式迎风差分格式考虑到上游控制体的温度，因而能够保证较高的计算精度．同时，在每次计算中，为了得到每个控制体的温度，只需要考虑前一时刻管道的温度分布以及该时刻上游控制体的温度，而这些温度在计算过程中为已知量．因此，隐式迎风差分方法能够实现高效的管道热动态分析．此外，隐式迎风差分格式在计算过程中无条件稳定，具有较好的数值仿真性能．

将热动态模型从单个供热管道扩展到管网，并结合管网的初始温度分布、热源供水温度以及通过水力模型获得的管网流量和流向的分布状况，即可得到管网中温度的动态分布．

1.3 供热管网水力-热力耦合模型求解流程的热动态模型

对于大型环状集中供热管网，热水在环状管网中进行输送时的流向可能会发生变化，因此在水力-热力耦合模型中需要确定管网中每根管道的入口边界条件．本文采用的是有向图拓扑排序算法中的广度优先遍历方法，该方法的优势是可以系统遍历各个管段，并寻找到与源点相互连接的节点．对于大型集中供热管网，确定入口边界条件的广度优先遍历方法的流程如下：

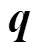
(5) 重复步骤(3)和(4)直到所有节点的访问标志都已更新．

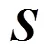
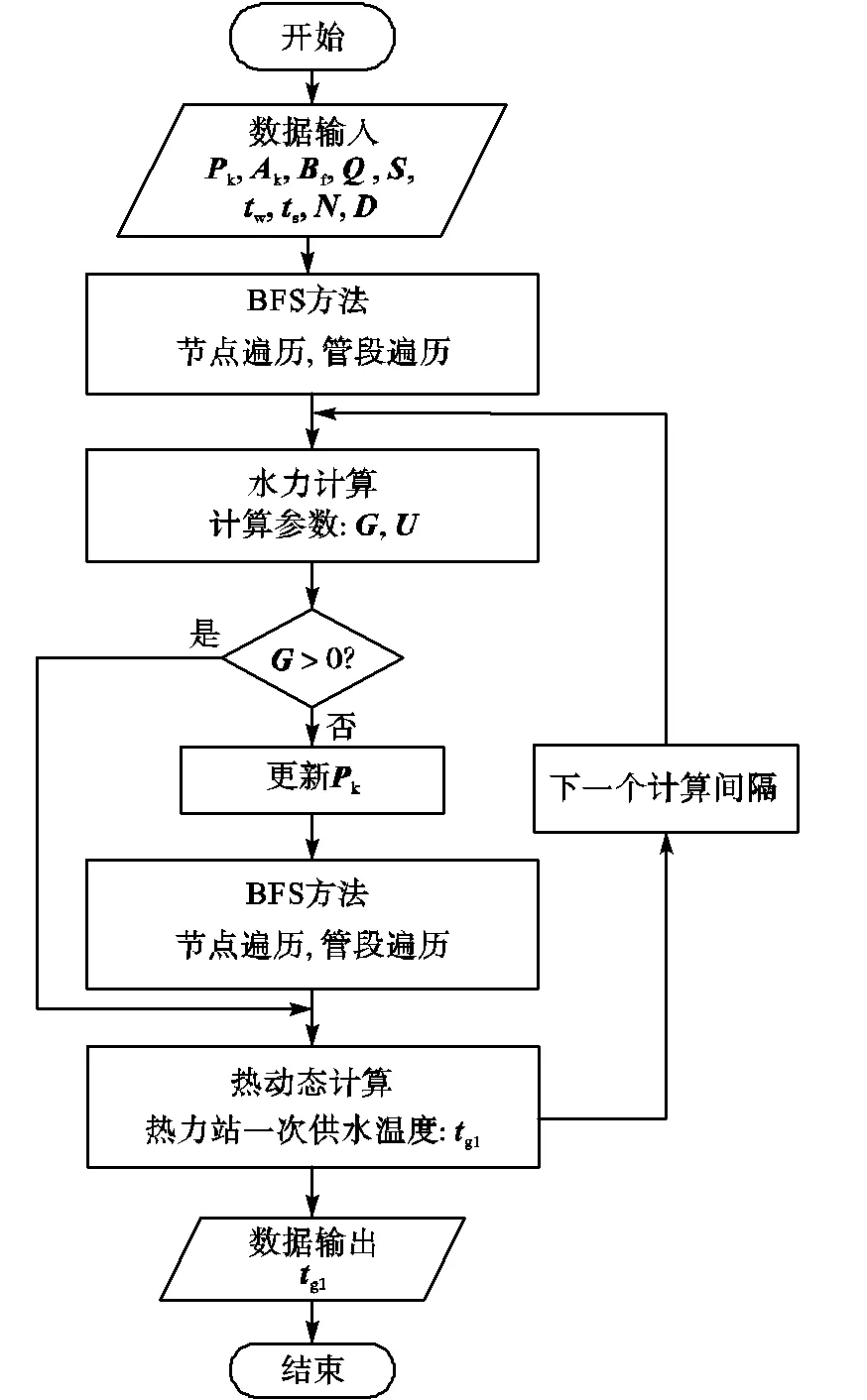
图2 水力-热力耦合模型的计算流程

1.4 供热管网水力-热力耦合模型的验证

图3为天津市某区域的集中供热管网示意，该管网具有3个热源，每个热源处设有3台水泵同时运行，区域管网中建有413座热力站，共有21个环、891个管段以及871个节点．管网一次侧为质调节运行方式，其设计供回水温度为130℃/70℃，整个管网的末端形式有地板辐射、散热器以及风机盘管．热源流量、压力和供回水温度等数据每分钟记录1次，中继加压泵站处流量和压力信息每分钟记录1次，热力站处一、二次供/回水温度、流量和压力等数据每5min记录1次，室外温度每小时记录1次．

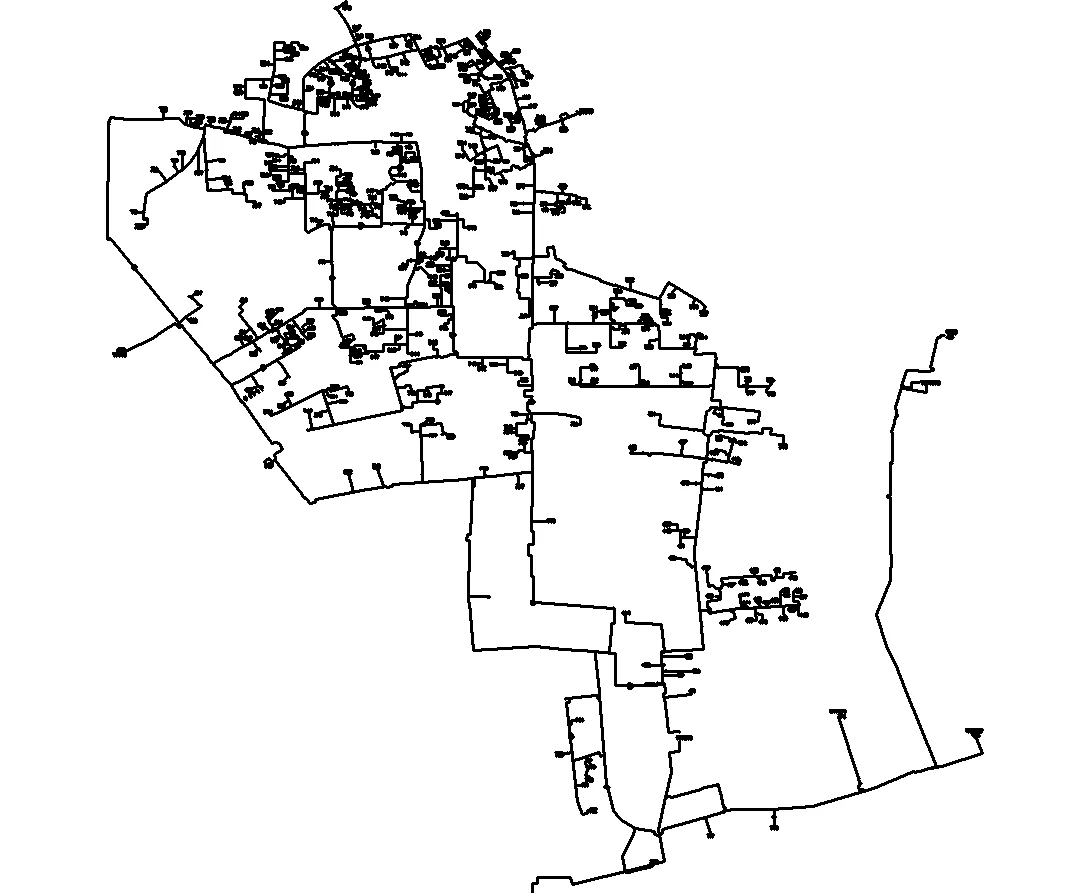
图3 管网布局示意

将上述算法采用Matlab编程实现，利用实际运行数据验证模型的准确性．利用冬季供暖季某日06:00至21:00时间段内各热力站和热源运行流量、压力、热量等数据进行验证．

图4为选取的5个热力站供水压力计算值与监测值的对比情况．根据图4和图5，运行期间内，热力站供水压力波动范围为0.62～0.76MPa，各个热力站供水压力变化趋势基本一致，因而采用基本回路法能够较好地描述热力站的供水压力变化．

图6～图9显示了室外温度以及3个热源的供水温度的详细变化情况，室外温度在该时间段内的变动范围为-2.0～5.0℃，并且呈先升高再降低的趋势．在监测期间，3个热源温度均呈现出明显波动．由于热源2在此期间对管网出力较小，因而其温度波动较其他两个热源幅度小．

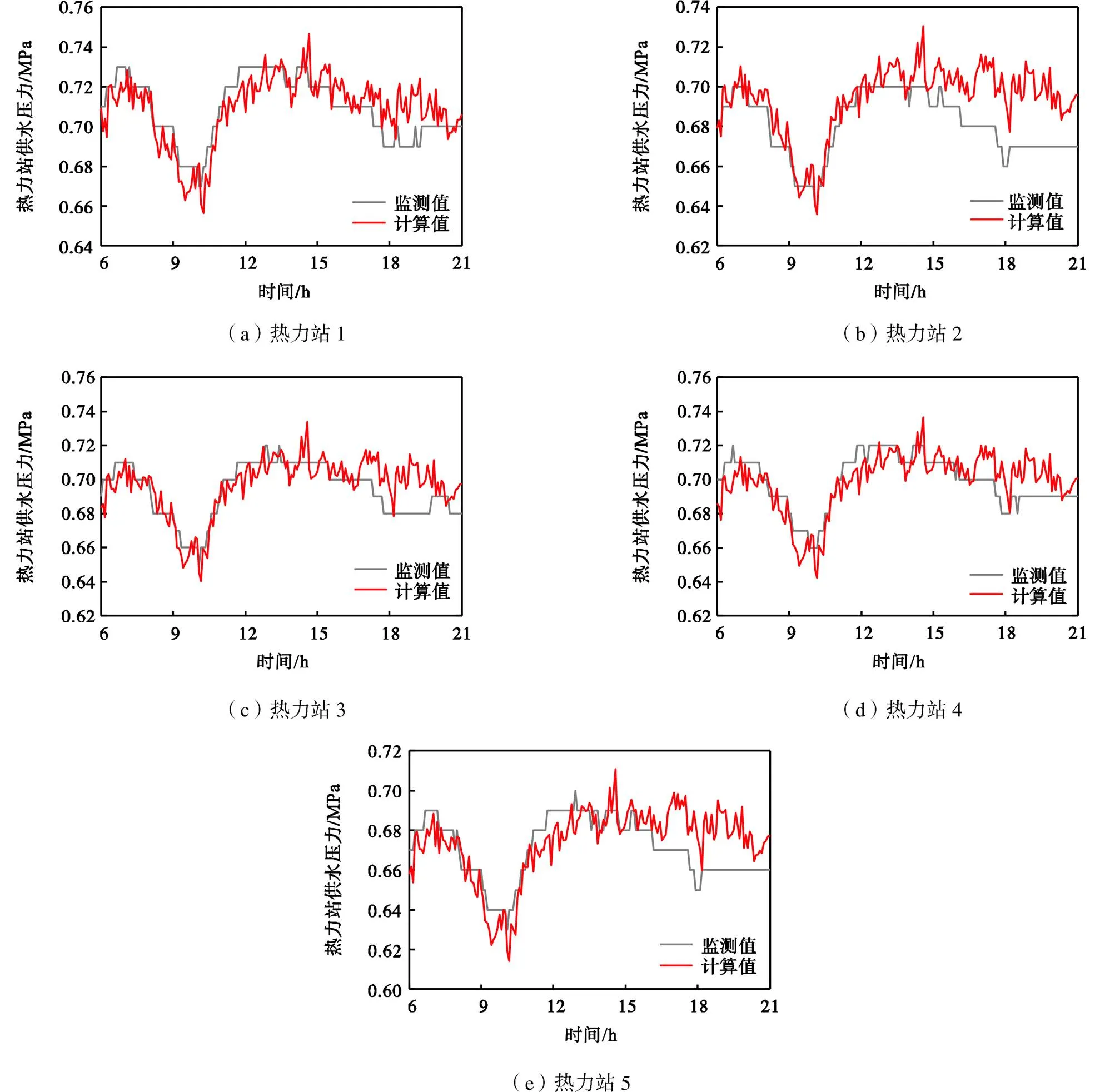
图4 部分热力站供水压力监测值与计算值对比

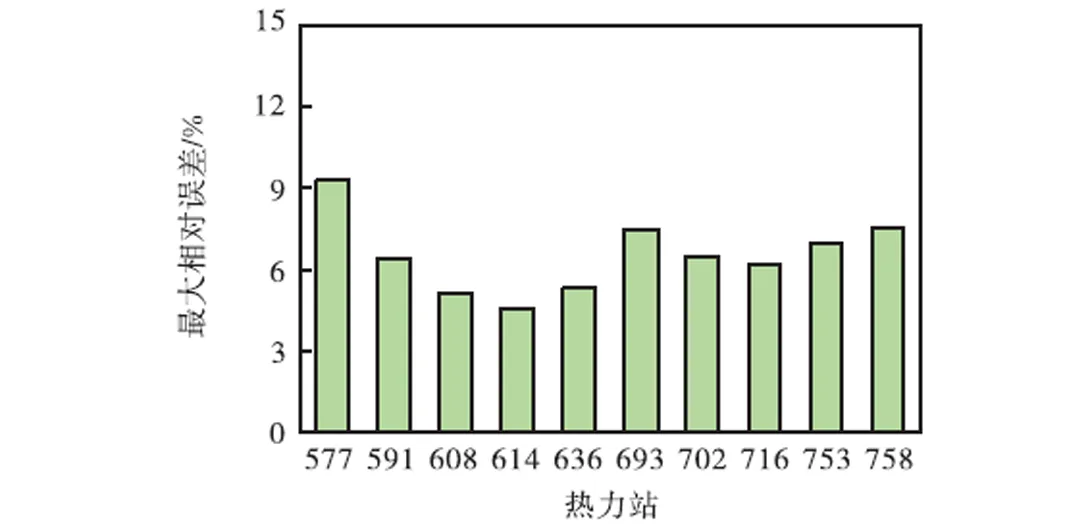
图5 供水压力计算相对误差

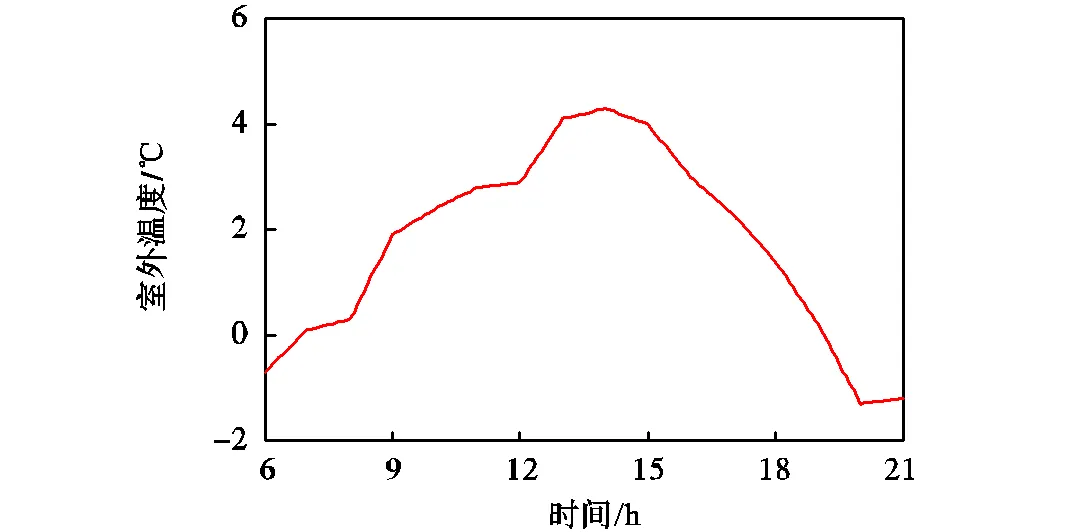
图6 监测时间段内室外温度的变化情况

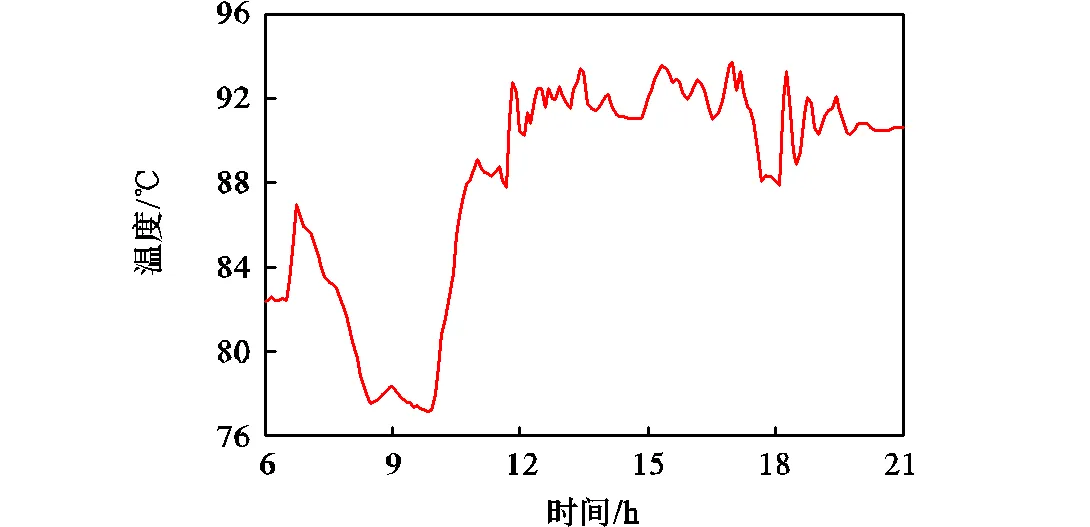
图7 监测时间段内热源1温度变化

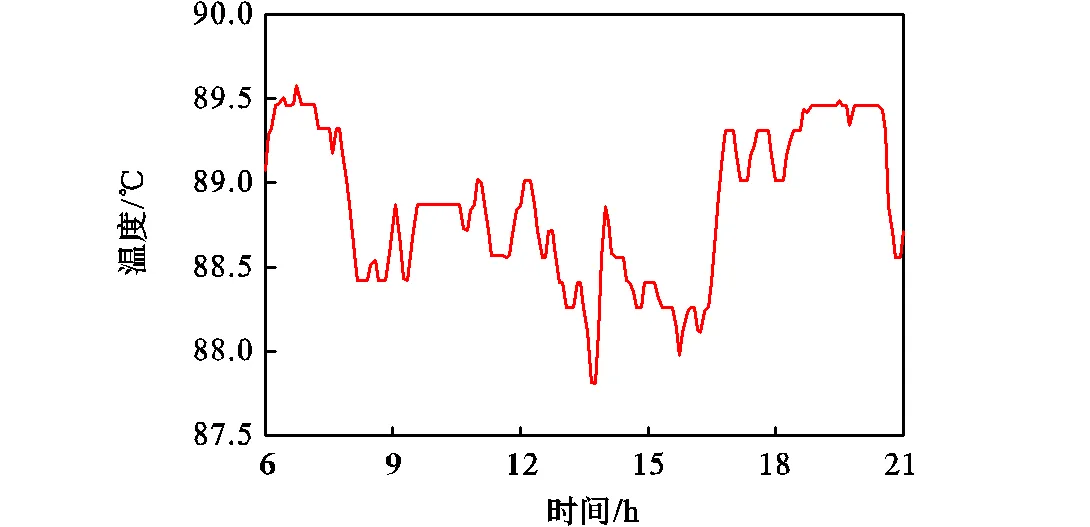
图8 监测时间段内热源2温度变化

图10显示了监测时间段内热力站一次侧供水温度计算值与监测值的变化情况，可以看出计算值与监测值整体很接近．图11和图12为多个热力站监测值与计算值的绝对误差和相对误差值的变化，可以看出，热力站绝对误差均在4.5℃之内，且相对误差均不超过6.0%，可以验证所建立的水力-热力耦合模型能够实现较高精度的热动态仿真分析．

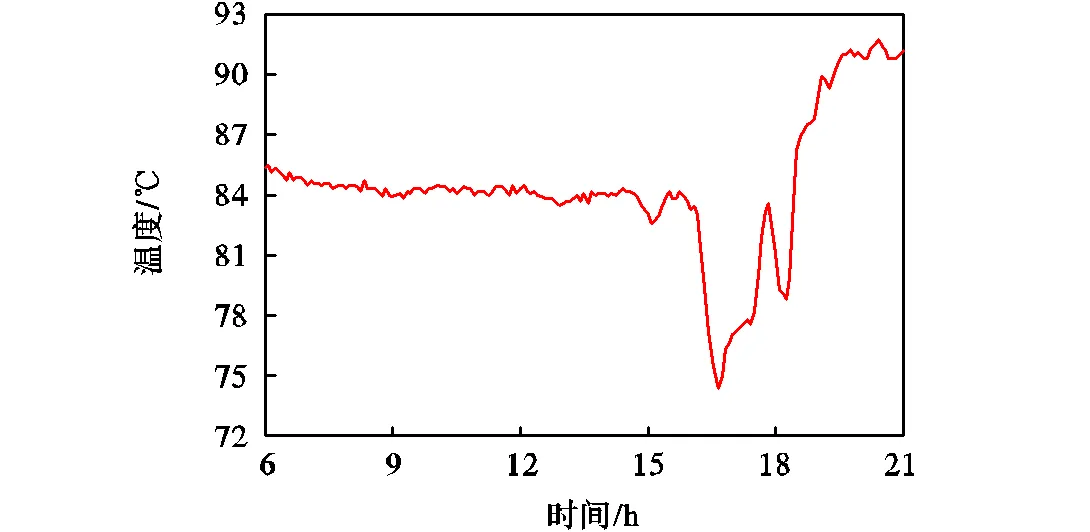
图9 监测时间段内热源3温度变化

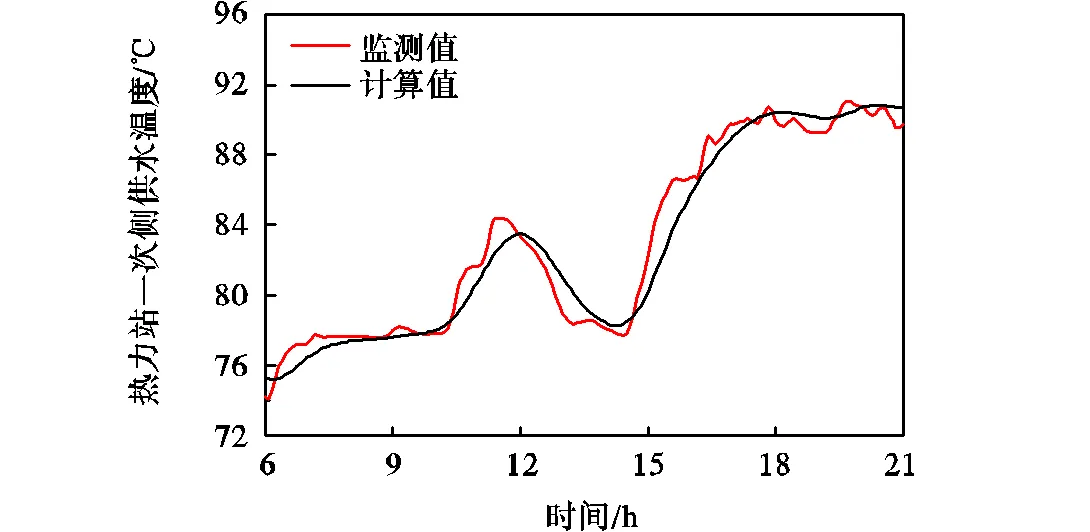
图10 监测时间段内热力站一次侧供水温度变化

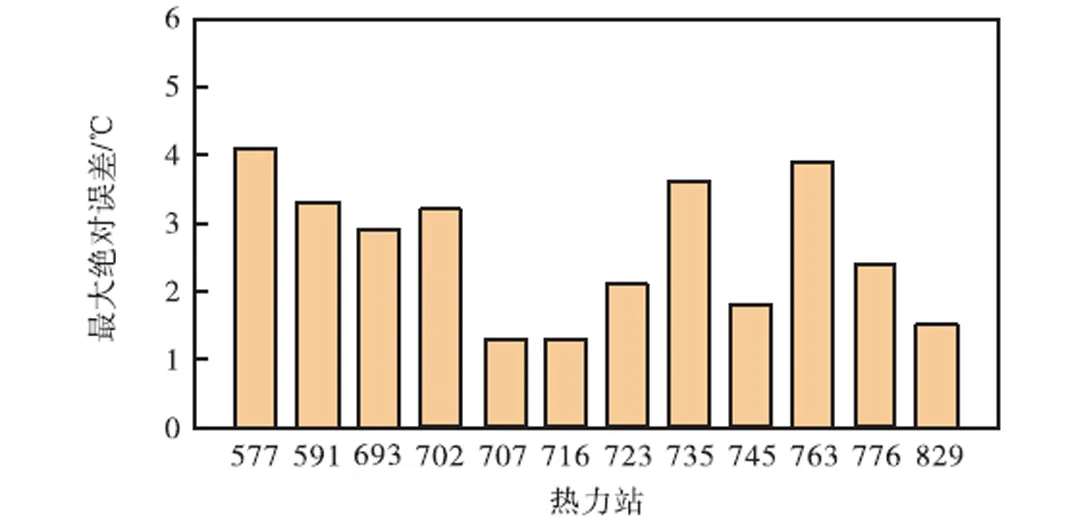
图11 部分热力站监测值与计算值绝对误差

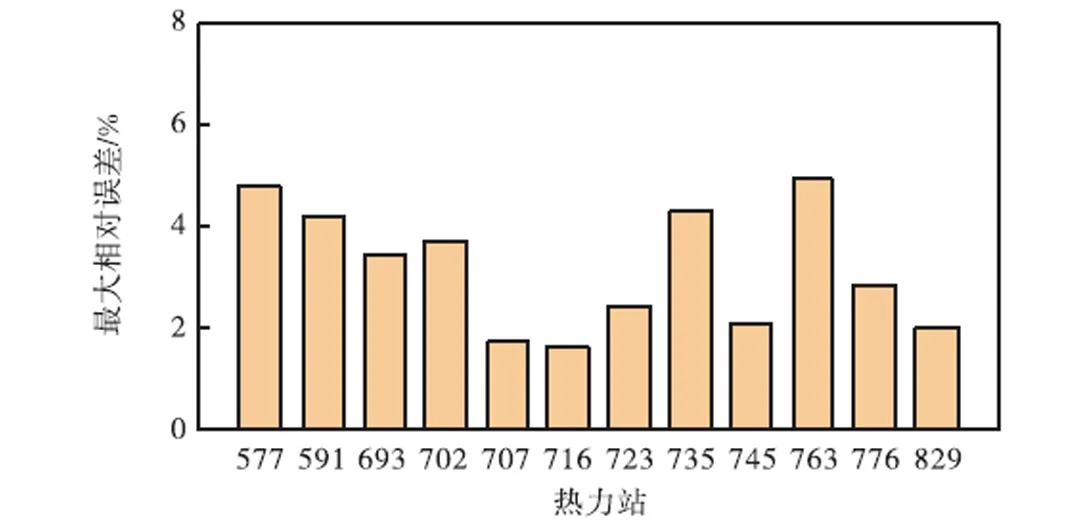
图12 部分热力站监测值与计算值相对误差

2 集中供热系统的能耗计算模型

在大型集中供热系统中，管网在运行调节过程中所产生的能耗主要由水泵运行的电耗和管网的散热损失组成．

2.1 供热管网沿程散热损失及折合费用

根据第1节建立的管网水力-热力耦合模型，可以计算出供、回水管网在每个时间步长下的散热损失.单个管道的散热损失为各控制体散热损失之和，单个控制体在单位时间的散热损失计算式为

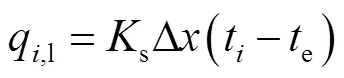
对于一个划分为个控制体的管道，单位时间内沿管长方向的散热损失为

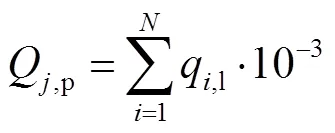
对于由根管道组成的集中热网，单位时间内管网的散热损失为

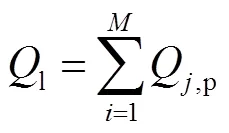
由于管网热损失导致的运行费用可用式(16)、(17)计算．

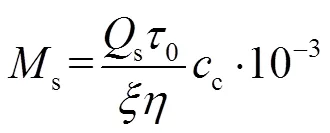
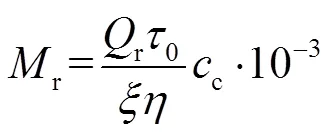
2.2 供热管网水泵能耗及折合费用

单台水泵功率的计算式为

集中供热管网中通常有多台水泵同时运行，则系统中水泵的总功率为

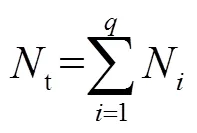
式中：t为供热系统中水泵的总功率，kW；为供热管网中运行中水泵的个数．

由于水泵能耗折合的费用可表示为

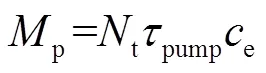
供热系统在运行时的总能耗可表示为

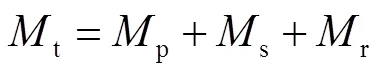
3 基于粒子群优化算法的优化调度模型

3.1 粒子群优化算法的基本原理

粒子群优化(PSO)算法是一种人工智能算法，源于鸟类觅食行为，最早由Kelinedy和Eberhart提 出[21]，PSO算法是通过群体内部个体的合作进行不断更新从而找到最优解的．

在PSO算法中，每个粒子即为PSO维搜索空间的一个个体，具有位置和速度两个属性，在进行搜索的过程中，粒子群通过不断寻找每个粒子的最佳位置(个体极值)和全体粒子的最佳位置(全局极值)进行速度和位置的更新：

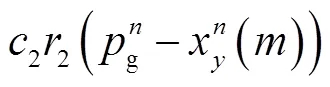
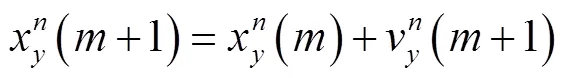
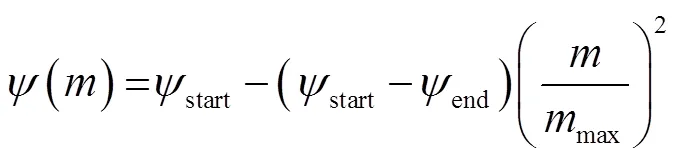
3.2 环状管网优化调度模型

本研究将最小化管网输配损耗的总成本作为供热管网优化调节的目标函数，将满足管网的回路压力平衡方程、满足节点的质量守恒方程、热力站入口阀门开度介于0～100%之间、热源供水温度不超过设计供水温度作为约束条件进行建模，即

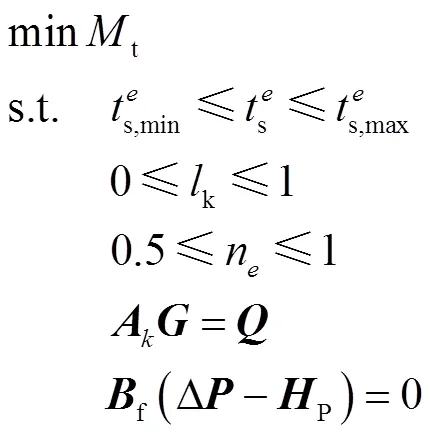
大型多热源环状管网为非线性动态系统，其调度优化问题较为复杂，优化过程中涉及的参数较多，且优化难度较大，本文采用PSO算法对其进行求解．

3.3 基于粒子群优化算法的供热管网优化调度模型求解流程

在本文的模型中，控制变量的个数对应于PSO算法中的空间维数PSO，本文中控制变量为热源供水温度和热力站处阀门开度，因此控制变量个数为热源数量与阀门个数之和；热源供水温度与阀门开度的不同组合对应着不同位置的粒子，使得管网总运行费用最小的参数组合，即为PSO中的群体极值．具体的计算步骤如下.

(1) 热力站负荷预测．

(2) 参数初始化：给出粒子数、最大迭代次数、个体学习因子和社会学习因子，确定惯性因子的最大值和最小值，确定算法的空间维度PSO，即需要控制的热源个数以及阀门个数，确定热源供水温度的变化范围以及阀门开度范围，随机分配热源供水温度和阀门开度初始值及其变化量，初始化每个粒子的最优历史位置，并随机假定种群中的最优粒子．

(3) 管网输配损耗的总成本的计算：根据给定的热源供水温度及阀门开度，对供水管网进行水力-热力耦合分析，初步计算管网总运行费用．

(4) 单个粒子最佳位置的更新：将每个粒子计算所得的管网总运行费用与其历史最佳位置所对应的管网总运行费用进行对比，若此次迭代中对应的费用更低，则将该粒子的当前位置替换为其历史最佳位置，否则该粒子的历史最佳位置保持为原始位置．

(5) 群体最佳位置的更新：计算所有粒子最佳位置对应的管网总运行费用，将管网最小运行费用与上一次迭代中群体最佳位置所对应的运行费用对比，若前者较小，则将群体最佳位置替换为运行费用最小的粒子位置，否则群体最佳位置仍保持上一次迭代中的群体最佳位置．

(6) 参数更新：更新惯性因子，更新所有粒子的位置和速度．

(7) 重复步骤(3)～(5)直至进行到最大迭代 次数．

3.4 实例分析

本节将选取天津市某区域供热管网进行实例计算分析．

冬季供暖室外计算温度取－7.0℃，其热源的设计供/回水温度为130℃/70℃．假设各个热力站为连续24h全天供热，对于末端为散热器的热力站，其二次设计供/回水温度为85℃/60℃，末端为地板辐射采暖的热力站，其二次设计供/回水温度为50℃/40℃．在管网实际运行过程中，只有热力站处阀门可以调节，其他管段上为不可调节阀门．

在进行优化调度计算时，种群搜索空间维度设置为4维，粒子数为30个，迭代步数设置为1000步，达到迭代步数时计算终止．

图13为相应工况下热力站总负荷和管网运行费用计算结果，可以看出，热力站总负荷与室外温度无正相关性，这是由于管网具有输配延迟属性，导致热力站总负荷变化对室外温度变化的时间序列存在一定的时间滞后，从而呈现出数据上的非相关性．随着热力站总负荷的增大，相应的管网运行费用也随之增加，当室外温度分别为-0.6℃和3.8℃时，管网的运行费用对应为80元/min和68元/min．

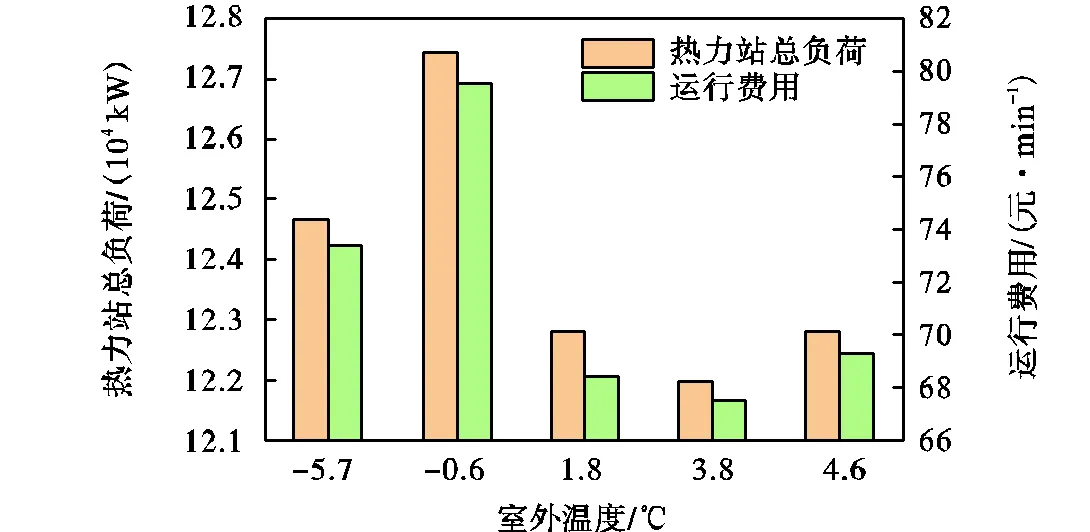
图13 不同工况下总负荷和管网运行费用

由图14和表1可以看出，水泵运行费用与管网总运行费用变化趋势一致，这说明虽然热力站阀门开度变化较小，但对系统的水力状况影响较大．此外，不同工况下各个热源的供水温度有所区分，考虑到室外温度升高时，管道向外传热较少，因而管网的热损费用随着室外温度的增大而减小．

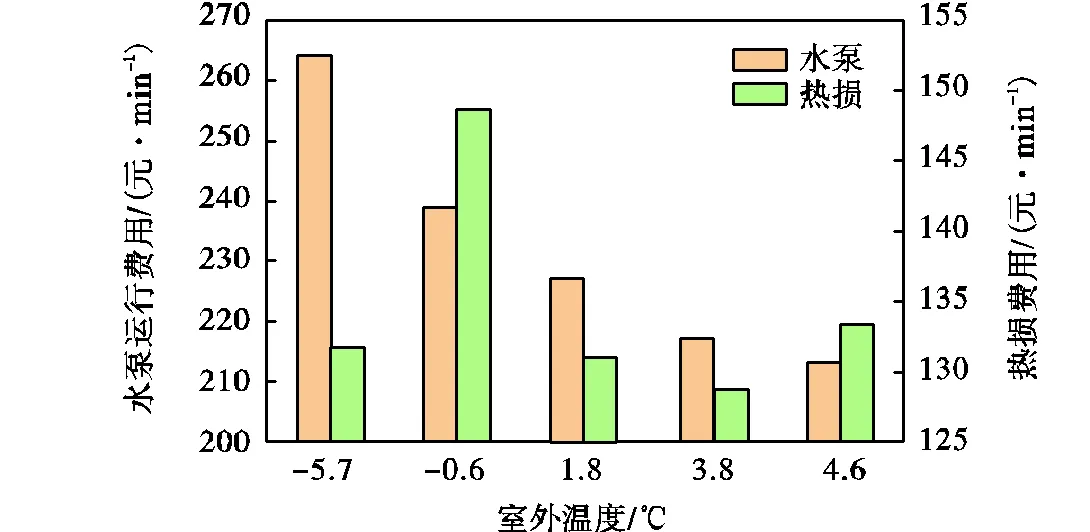
图14 不同工况下水泵和热损费用

表1不同工况下热源供水温度及热力站阀门开度

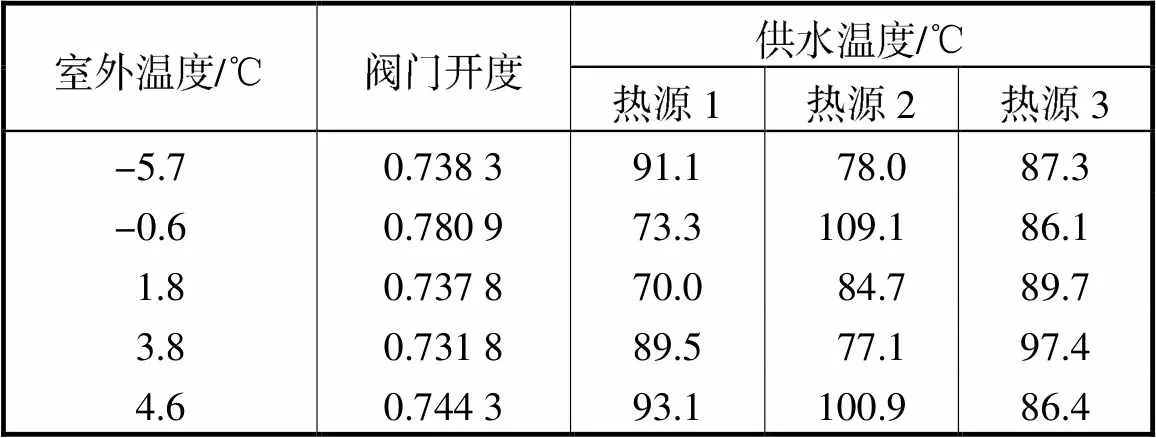
Tab.1　　Water supply temperature of heat source and valve opening of a heating station under different working conditions

图15为水泵运行费用以及供/回水管网热损费用的占比情况，可以看出，水泵运行费用为整个管网运行费用的主要组成部分，占总运行费用的58%以上．管网热损由供水管网热损和回水管网热损这两部分组成，由于供水温度较回水温度高，回水管网热损约为供水管网热损的1/2．

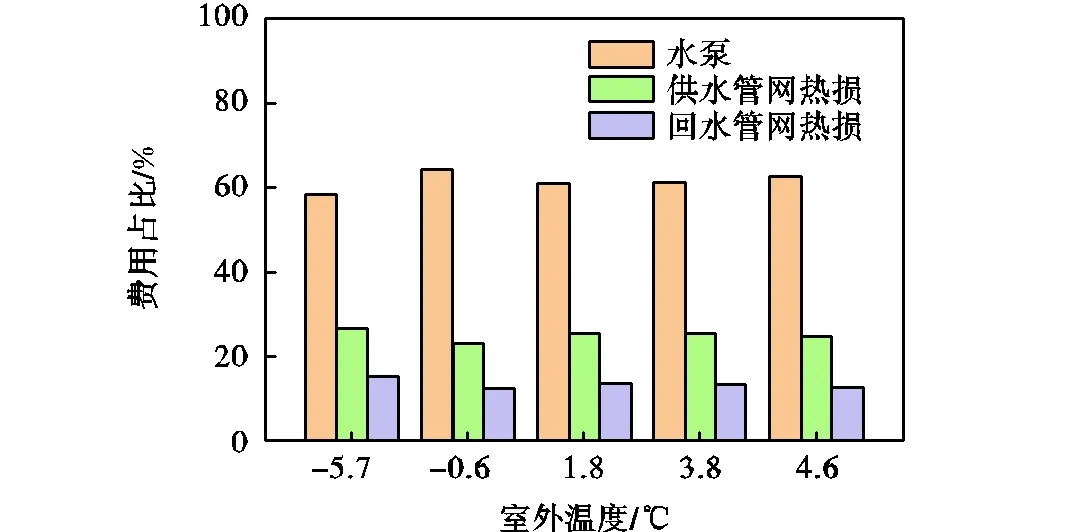
图15 不同室外温度下各种运行费用占比

4 结 论

本文针对大型多热源环状管网的优化调度问题，分别建立管网的水力-热力耦合模型、能耗计算模型和优化调度模型，给出了各个模型的求解方法和求解流程，并结合实际管网进行了分析计算，结果如下.

(1) 建立的管网的水力-热力耦合模型是大型管网运行调节分析的基础，给出的广度优先遍历方式和隐式迎风差分格式是求解供热管网水力-热力耦合模型的有效方法．

(2) 建立了供热管网系统运行能耗计算的模型，并进行了分析计算，在本例的运行调节计算中，水泵的能耗占管网运行总能耗的近60%，管网的热损失约占管网运行总能耗的40%．

(3) 粒子群优化算法结合管网的优化调度的模型，是解决供热管网运行调节的一个有效方法，该方法既能很快收敛，又能找到模型的最优解，为智慧供热提供了参考．

［1］ Oppelt T，Urbaneck T，Gross U，et al. Dynamic thermo-hydraulic model of district cooling networks[J]. Applied Thermal Engineering，2016，102：336-345.

［2］ Liu X Z，Wu J Z，Jenkins N，et al. Combined analysis of electricity and heat networks[J]. Applied Energy，2016，162：1238-1250.

［3］ Wang H，Meng H. Improved thermal transient modeling with new 3-order numerical solution for a district heating network with consideration of the pipe wall’s thermal inertia[J]. Energy，2018，160：171-183.

［4］ 王庆峰. 集中供热系统运行调节优化及热负荷预测方法研究[D]. 济南：山东大学，2010.

Wang Qingfeng. Study on Operation Regulation Optimization and Heat Load Forecasting Method of Central Heating System[D]. Jinan：Shandong University，2010(in Chinese).

［5］ 周守军. 基于管网动态模型的城市集中供热系统参数预测及运行优化研究[D]. 济南：山东大学，2012.

Zhou Shoujun. Research on Parameter Prediction and Operation Optimization of Urban Central Heating System Based on Pipe Network Dynamic Model[D]. Jinan：Shandong University，2012(in Chinese).

［6］ 时国华，杨林棣，张 浩，等. 集中供热系统多热源调度优化模型[J]. 热力发电，2020，49(3)：68-75.

Shi Guohua，Yang Linli，Zhang Hao，et al. Multi heat source scheduling optimization model of central heating system[J]. Thermal Power Generation，2020，49(3)：68-75(in Chinese).

［7］ Stevanovic V D，Zivkovic B，Prica S，et al. Prediction of thermal transients in district heating systems[J]. Energy Conversion and Management，2009，50：2167-2173.

［8］ Liu X Z，Wu J Z，Jenkins N，et al. Combined analysis of electricity and heat networks[J]. Applied Energy，2016，162：1238-1250.

［9］ Hassine I B，Eicker U. Impact of load structure variation and solar thermal energy integration on an existing district heating network[J]. Applied Thermal Engineering，2013，50：1437-1446.

［10］Vesterlund M，Toffolo A，Dahl J. Simulation and analysis of a meshed district heating network[J]. Energy Conversion and Management，2016，122：63-73.

［11］Zhou S J，Li H M，Gong P，et al. Hydraulic modeling of double-source and ring-shaped heating networks[J]. Applied Thermal Engineering，2017，119：215-221.

［12］付祥钊，肖益民. 流体输配管网[M]. 北京：中国建筑工业出版社，2010.

Fu Xiangzhao，Xiao Yimin. Fluid Transmission and Distribution Network[M]. Beijing：China Architecture & Building Press，2010(in Chinese).

［13］米雷洋. 基于粒子群算法的大型多热源环状管网优化调度技术研究[D]. 天津：天津大学环境科学与工程学院，2018.

Mi Leiyang. Research on Optimal Scheduling of District Heating Network with Ring Topology and Multiple Heat Sources Based on Particle Swarm Optimization[D]. Tianjin：School of Environmental Science and Engineering，Tianjin University，2018(in Chinese).

［14］Duquette J，Rowe A，Wild P. Thermal performance of a steady state physical pipe model for simulating district heating grids with variable flow[J]. Applied Energy，2016，178：383-393.

［15］Steer K C B，Wirth A，Halgamuge S K. Control period selection for improved operating performance in district heating networks[J]. Energy and Buildings，2011，43：605-613.

［16］Wang Y R，You S J，Zhang H，et al. Thermal transient prediction of district heating pipeline：Optimal selection of the time and spatial steps for fast and accurate calculation[J]. Applied Energy，2017，206：900-910.

［17］Versteeg H K，Malalasekera W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method[M]. 2nded.England：Pearson Education Limited，2007.

［18］Zheng X，Shi K，Wang Y，et al. Performance analysis of three iteration-free numerical methods for fast and accurate simulation of thermal dynamics in district heating pipeline[J]. Applied Thermal Engineering，2020，178：115622.

［19］Wang Y，Shi K，Zheng X，et al. Thermo-hydraulic coupled analysis of meshed district heating networks based on improved breadth first search method[J]. Energy，2020，205：117950.

［20］Zheng X，Sun Q，Wang Y，et al. Thermo-hydraulic coupled simulation and analysis of a real largescale complex district heating network in Tianjin[J]. Energy，2021，236：121389.

［21］Kelinedy J，Eberhart R C. Particle swarm optimiza-tion[C]// Proceeding of IEEE International Confereece on Neural Networks. Piscataway，USA，1995：1942-1948.

Optimal Dispatching of District Heating Network Based on Dynamic Hydraulic-Thermal Coupling Model

Li Hong1, 2，Zhang Huan1，Wang Yaran1，Mi Leiyang2，Shi Kaiyu3，You Shijun1

(1. School of Environmental Science and Engineering，Tianjin University，Tianjin 300350，China；2.Tianjin Urban Planning & Design Institute Co.，Ltd.，Tianjin 300190，China；3. The Architectural Design & Research Institute of Zhejiang University Co.，Ltd.，Hangzhou 310028，China)

During the operation of the urban district heating network，the transmission and distribution consumption of the district heating system comprises the energy consumption of the circulation pump and the heat loss of the network. Reducing the transmission and distribution energy consumption of the district heating system is crucial to realizing low-carbon heating. This study establishes the dynamic hydraulic-thermal coupling simulation model of the district heating network，simulates the actual heating pipe network operation in Tianjin and validates the accuracy of the dynamic hydraulic-thermal coupling simulation model using the actual operation data based on the network graph theory，fluid transmission as well as distribution principle，and one-dimensional heat transfer of pipelines. The transmission and distribution energy consumption model associated with the district heating network is established，and the economic analysis of the operating energy consumption is performed. An effective scheduling approach for a meshed district network with numerous heat sources is produced by integrating the particle swarm optimization(PSO) algorithm. This method uses the lowest cost of total heating network transmission and distribution loss as the objective function；the supply temperature of the heat source，the speed ratio of the heat source pump，and the valve opening at the entrance of heating stations as decision variables；and energy and mass conservation as constraints. The calcu-lation stages for optimal network scheduling based on the PSO algorithm are provided via algorithm parameter match-ing. The regulating process of the optimal scheduling approach is investigated using the actual network in Tianjin as a case study. The results obtained via the simulation reveal that there is no static positive correlation between the total load variation of the heating station and the outdoor temperature variation owing to the network’s transmission and distribution delay properties. Furthermore，the operation cost of the pumps is shown to be the critical component of the entire pipe network operational cost，accounting for more than 58% of the total operational cost. This study pre-sents a set of effective calculation tools for optimizing the operation and regulation of urban central heating networks.

district heating network；particle swarm optimization algorithm；operation regulation；energy consumption analysis；dynamic hydraulic-thermal coupling model

TK995.3

A

0493-2137(2023)01-0027-10

10.11784/tdxbz202112005

2021-12-03；

2022-03-10.

李 鸿（1984—  ），男，博士研究生，高级工程师，lh254140391@126.com.

王雅然，yaran_wang@tju.edu.cn.

国家自然科学基金资助项目(52008290).

Supported by the National Natural Science Foundation of China(No. 52008290).

(责任编辑：田 军)