一种基于鲸鱼优化的TOA/AOA最优化定位算法

秦 杰，邓 平，罗 锐，夏渔平

一种基于鲸鱼优化的TOA/AOA最优化定位算法

秦 杰1，邓 平1，罗 锐2，夏渔平1

（1.西南交通大学 信息科学与技术学院，成都 610097；2.成都师范学院 计算机学院，成都 611130）

针对非视距（NLOS）环境下，基于最优化原理的无线定位算法在迭代运算后期容易陷入局部最优，进而导致定位精度下降的问题，提出一种基于非线性、自适应、动态惯性权重的鲸鱼优化到达时间（TOA）/到达角（AOA）最优化定位算法：基于双基站定位场景建立TOA/AOA混合定位模型；并且在对种群位置进行初始化时，在混合线性定位算法中增加角度约束条件避免种群在定位初期陷入局部最优；然后在搜索更新最优个体时，引入自适应动态惯性权重系数对鲸鱼优化算法进行改进，以更好地协调优化算法的全局随机搜索与局部寻优能力。仿真结果表明，与现有的粒子群优化（PSO）、鲸鱼优化（WOA）和改进的鲸鱼优化（MWOA）等智能优化算法相比，所提算法在迭代寻优过程中具有更快的收敛速度和更优的收敛精度；相较于WOA算法，其平均消耗时间可降低约50%，平均定位误差可降低约41%，定位性能更优。

鲸鱼优化算法（WOA）；非视距（NLOS）；智能优化；无线定位

0 引言

在移动互联网时代，基于位置的目标跟踪、智能交通、物联网和紧急救援等定位服务更加普及。随着第五代移动通信技术（fifth-generation，5G）基站在室内外环境大量部署，基于5G网络的无线定位技术在定位服务中得到更广泛的应用。然而无线定位中电波的非视距（non line of sight，NLOS）传播严重影响定位性能。如何抑制无线定位中无线信号NLOS传播导致的定位误差成为人们关注的热点。

基于最优化理论的无线定位算法因其良好的定位性能一直受到广泛关注[1]。文献[2]提出了2种基于多基站的混合到达时间（time of arrival，TOA）和到达角（angle of arrival，AOA）的定位算法，即混合TOA/AOA（hybrid TOA/AOA，HTA）算法和混合线性定位（hybrid lines of position，HLOP）算法，但这2种算法抑制NLOS误差的能力有限。文献[3]对文献[2]中的算法进行改进，通过在目标函数中加入散射体的位置坐标信息，提出了混合TOA/AOA约束算法（TOA/AOA constraint algorithm，TACA）；但该算法采用最优化理论中的内点法[4]来估计移动台的位置，性能受初始值影响较大，且容易陷入局部最优解。文献[5]中提出了一种应用于双基站场景的NEWTACA最优化定位算法，在原TACA算法的基础上，引入了一个隐藏的有关角度的非线性等式约束；但由于目标函数的高非线性和非凸性，NEWTACA算法同样可能会收敛到局部最优。为此，文献[5]中还通过引入智能优化算法，提出了一种网格搜索算法[6]，通过引入2个尺度因子进行搜索及最优化求解。除了上述解析算法外，粒子群算法（particle swarm optimization，PSO）[7]、人工神经网络（artificial neural network，ANN）[8-9]、哈里斯鹰算法（Harris hawk optimization，HHO）[10]等智能优化算法也被应用于最优化定位领域，并在一定程度上改善了定位性能。如文献[11]中提出了一种基于混沌粒子群优化算法的混合TOA/AOA定位算法，利用混沌理论进一步对PSO算法进行优化和改进，并且引入了自适应惯性权重策略，对算法中的惯性权重参数采用动态自适应变化的方式，在迭代过程中根据粒子所处的位置选择适合的惯性权重值，能够达到全局最优；但是该算法计算复杂度高，存在收敛速度慢的问题。文献[12]中将哈里斯鹰优化算法用于TDOA定位的非线性问题求解，对初始种群和适应度函数进行了优化，在一定程度上增强了搜索能力；但是仍然存在算法迭代运算后期容易陷入局部最优的问题，导致无法达到全局最优解。

如何解决最优化定位算法可能陷入局部最优的问题，一直是相关领域的重要课题。为此，本文提出一种基于鲸鱼优化的TOA/AOA最优化定位算法。首先在双基站定位场景下，建立TOA/AOA混合定位模型；接着提出一种基于自适应动态惯性权重的鲸鱼优化算法，并利用基站、移动台与散射体之间的几何位置关系，建立新的最优化目标函数和约束条件；然后在目标可行域内利用上述鲸鱼优化算法进行移动台最优位置的估计。

1 TOA/AOA混合定位模型

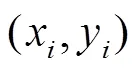
图1 基站与移动台几何分布

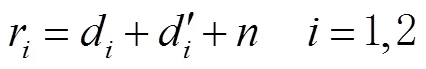
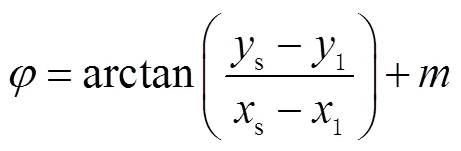
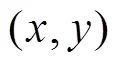
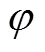
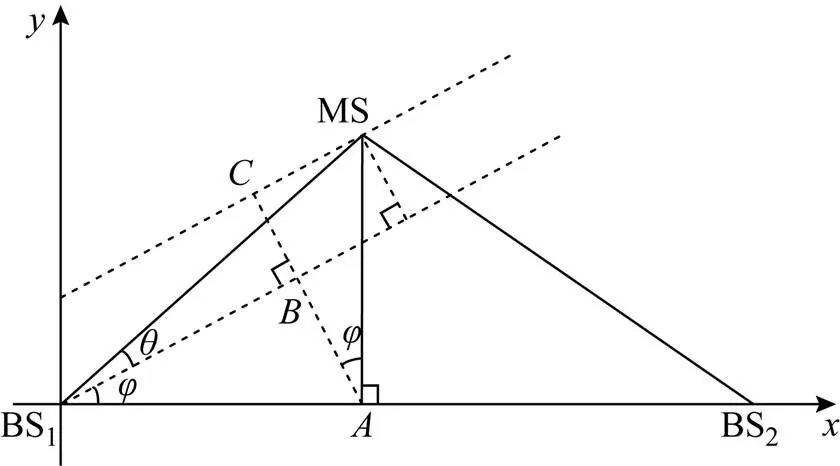
图2 AOA角度约束

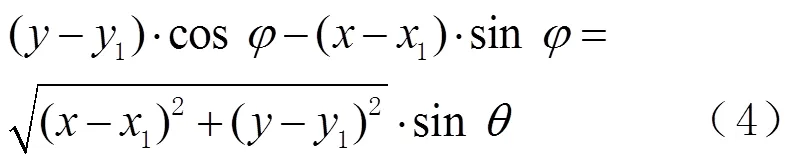
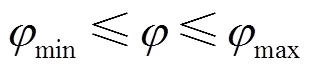
因此，双基站场景下的TOA/AOA混合定位模型可以建立为

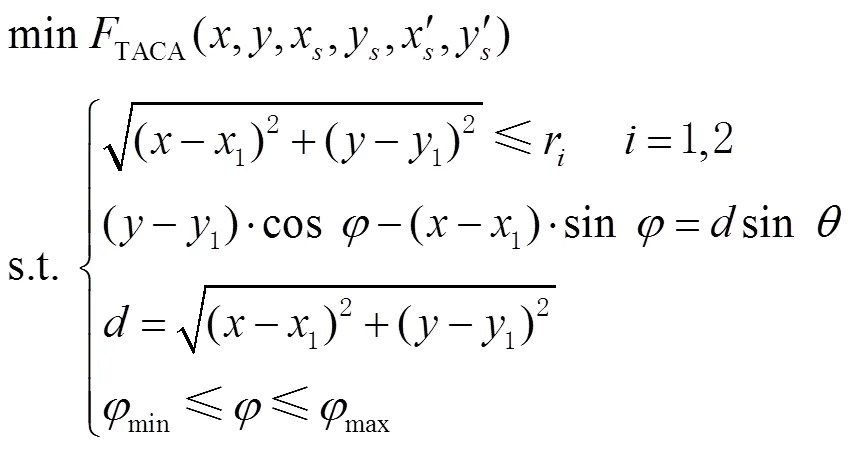
求解式（6）的常用方法是最优化理论中的内点法，但该方法的不足是容易陷入局部最优[14]，导致MS定位精度受损。

2 自适应动态权重鲸鱼优化定位算法

2.1 鲸鱼优化基本原理

鲸鱼优化算法（whale optimization algorithm，WOA）[15]是2016年由Mirjalili等人提出的一种模仿座头鲸的捕食行为的新型启发式优化算法，也是一种群体智能优化算法，其优点在于有较强的全局搜索能力和开发能力。基于鲸鱼捕食策略的WOA算法主要包含3个部分，即围猎场、泡泡网攻击（开发阶段）和搜寻猎物（探索阶段）。前2个部分通过收缩包围机制达到局部优化目的，而搜寻猎物通过随机搜索进行全局寻优。

包围猎场阶段：鲸鱼可以识别猎物的位置并包围它们，这种行为可以表示为：

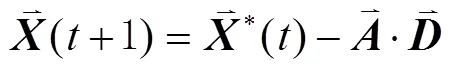
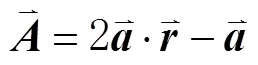
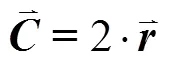
泡泡网攻击（开发阶段）：需要计算鲸鱼离目前群体最优值的距离，然后构建螺旋方程，模拟鲸鱼通过喷出气泡来驱赶猎物，进而更新位置，更新公式为

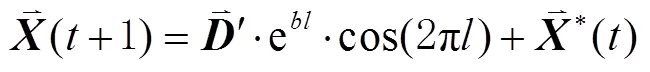
在鲸鱼更新位置时，包围猎场和泡泡网攻击机制是同步进行的，选择2种策略进行更新的概率均为50%，其数学模型表示为

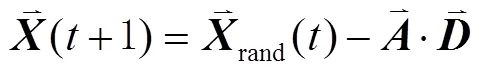
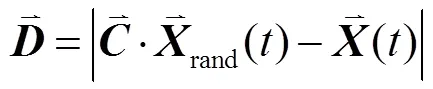
2.2 计算MS初始位置

HLOP算法[1]是一种混合TOA/AOA的线性定位算法。不同于HTA算法[1]和TACA算法[2]使用目标函数和约束条件，该算法将测距问题一阶线性化，计算过程简单且计算复杂度较低。本文采用文献[2]中的HLOP算法估计MS的初始位置，同时增加式（5）中的角度约束条件，命名为NEWHLOP算法。

2.3 自适应动态惯性权重策略

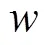
2）非线性自适应动态惯性权重策略。受文献[18]和[19]的启示，非线性自适应动态惯性权重策略可能更适合WOA算法实际搜索优化过程。本文在该文献基础上引入了变量迭代次数并且增加惯性权重的阈值判断，基于此提出本文的第二种自适应动态惯性权重策略。具体表达式为

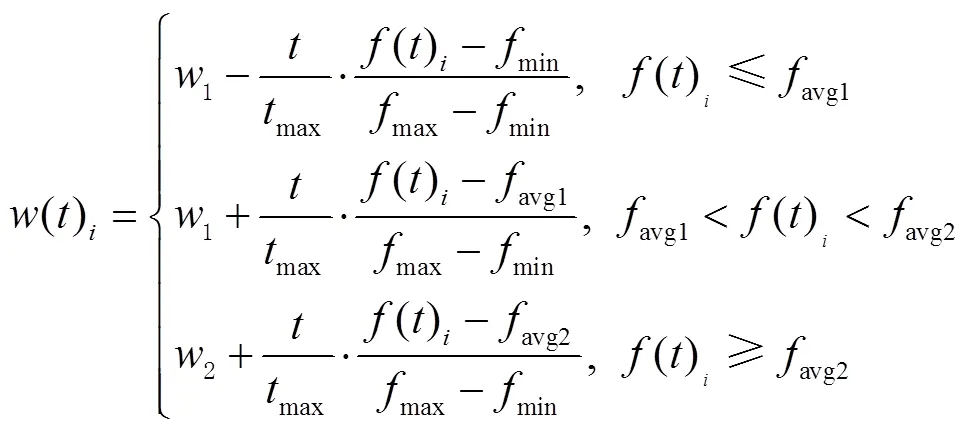
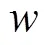
2.4 定位算法流程

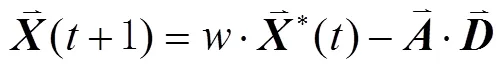
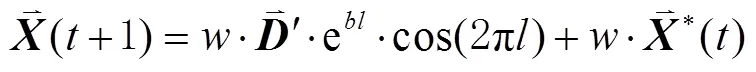
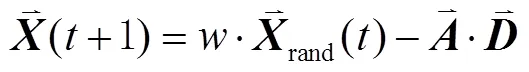
本文提出基于自适应动态惯性权重的鲸鱼优化定位算法（adaptive whale optimization algorithm，AWOA），算法流程如图3所示。具体步骤如下：

步骤1）初始化种群。将初始值设为NEWHLOP算法所确定的MS初始位置。

步骤2）计算种群适应度值。根据MS目标初始值计算出个体适应度值，并将最优个体设置为全局最优值。

图3 AWOA定位算法流程

步骤5）判断是否达到最大迭代数，如果是则输出最优估计值并终止迭代；否则返回步骤3）。

3 实验与结果分析

3.1 基准函数测试

为了检验本文提出的基于非线性自适应动态惯性权重的鲸鱼优化算法（AWOA）和其他群体智能优化算法的寻优性能，采用基准函数[20]进行仿真测试，并进行对比分析。

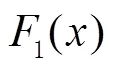
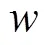
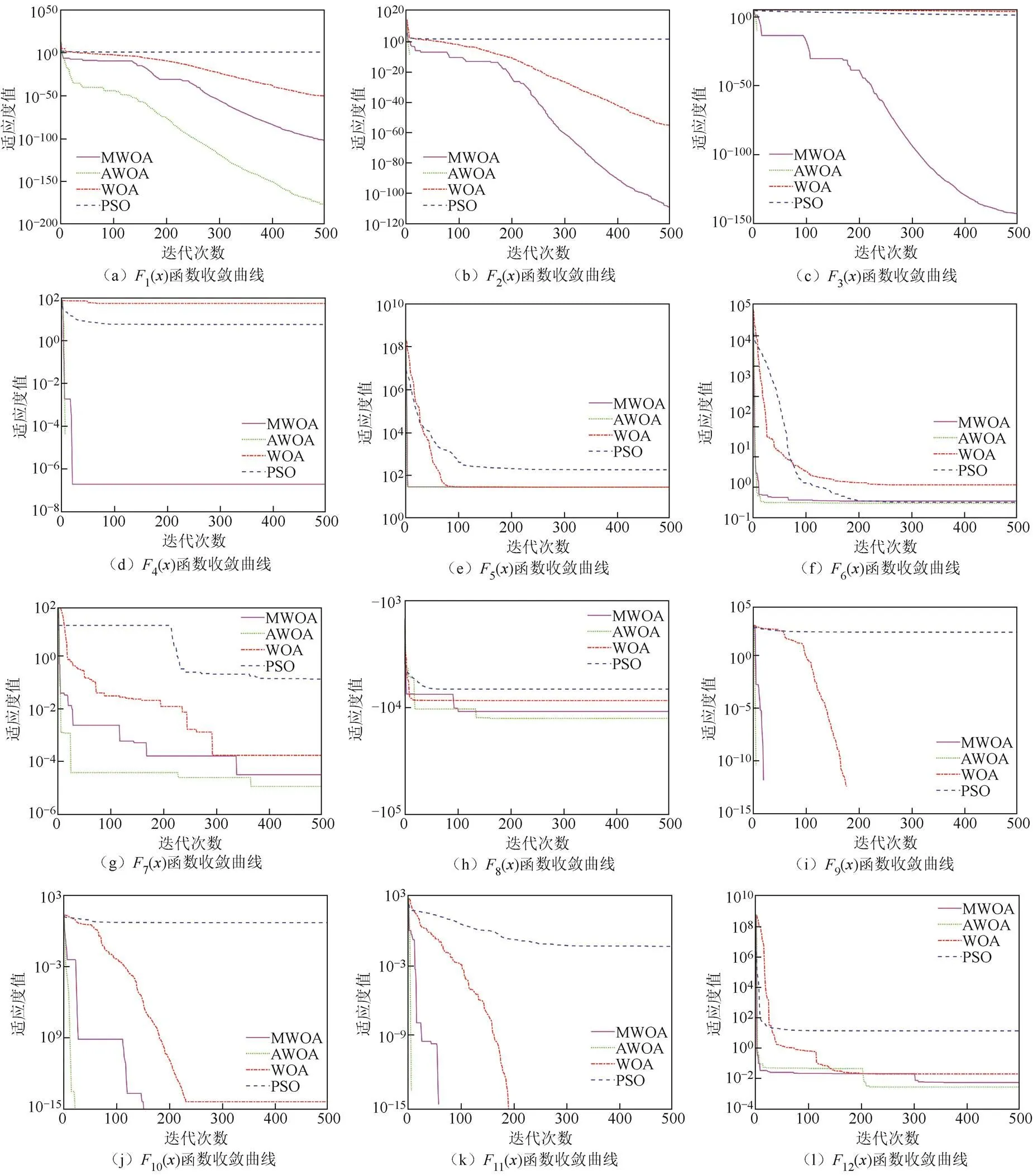
图4 基准测试函数收敛曲线

3.2 定位性能分析

将加入线性和非线性自适应动态惯性权重策略的鲸鱼优化定位算法（AWOA1和AWOA2算法）与传统的WOA算法、TACA算法、NEWTACA算法、网格搜索算法（grid-search-based algorithm，GSA）和NEWHLOP算法进行定位性能仿真分析。由3.1节中的仿真结果可知，针对大部分测试函数，最大迭代次数为40时即可收敛到最优值，因此本文算法迭代次数设置为40。此外，2种AWOA算法的其他参数设置与3.1节的参数相同。

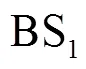
如图5所示为圆盘模型（disk of scatter，DOS）[13]下不同算法的定位误差累积分布函数（cumulative distribution function，CDF）曲线。从图中可以看出，本文中AWOA2算法的平均定位误差小于130 m以下的概率能达到100%，定位性能优于GSA智能优化算法和NEWTACA算法。

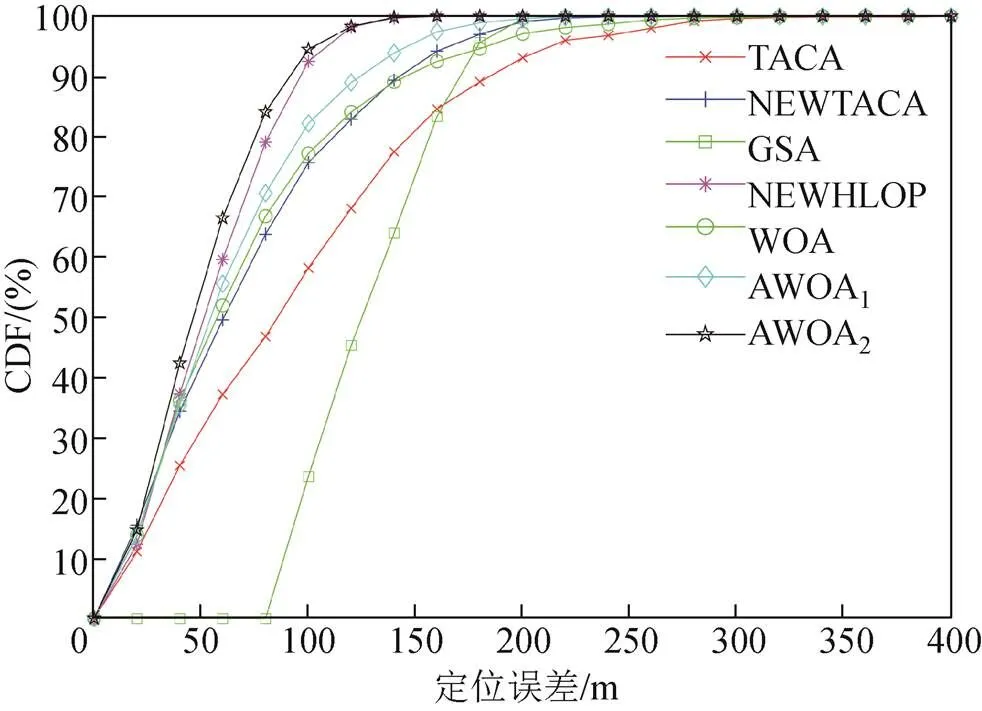
图5 DOS模型下的定位误差累计分布

固定AOA角度测量误差和TOA距离测量误差，改变散射体半径使其从100～300 m递增。如图6所示为DOS模型下不同算法相对于不同散射半径的平均定位误差（average location error，ALE）。从图可以看出，各算法的ALE均随着散射半径的增加而增加，这是散射半径的增加使得NLOS误差变大而导致的结果。本文AWOA2算法随着散射半径的增加始终表现出最低的ALE，从曲线总体趋势上看，本文算法误差增加得更为缓慢，说明AWOA2算法具有更强的NLOS误差抑制能力。

图6 DOS模型下ALE随散射半径的变化曲线

在DOS模型下，各算法相对于不同AOA角度测量误差和TOA距离测量误差的ALE性能曲线如图7和图8所示。从图中可以看出，ALE对TOA和AOA测量误差的变化均不敏感，但TACA算法和NEWTACA算法的ALE性能曲线相对波动较大，这是因为它们是基于内点法进行定位解算，容易陷入局部最优解；而智能优化算法由于良好的全局搜索能力表现出较强的鲁棒性，且在不同测量误差下，AWOA2算法平均定位误差明显低于其他对比算法，验证了本文算法具有较优的定位性能。

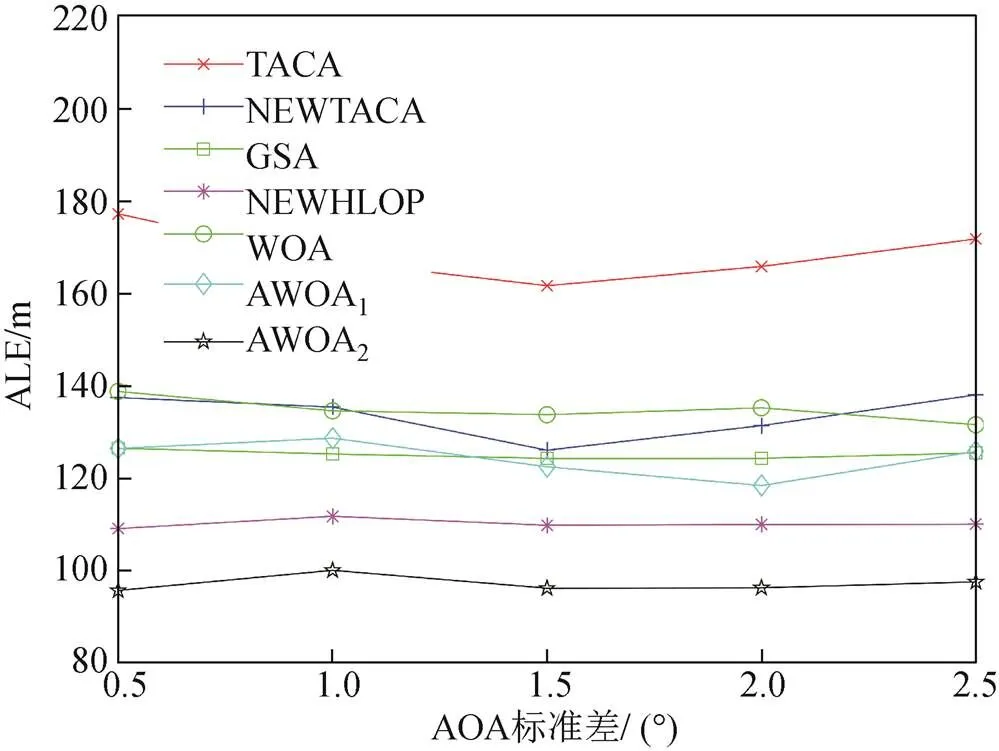
图7 ALE随角度测量误差的变化曲线

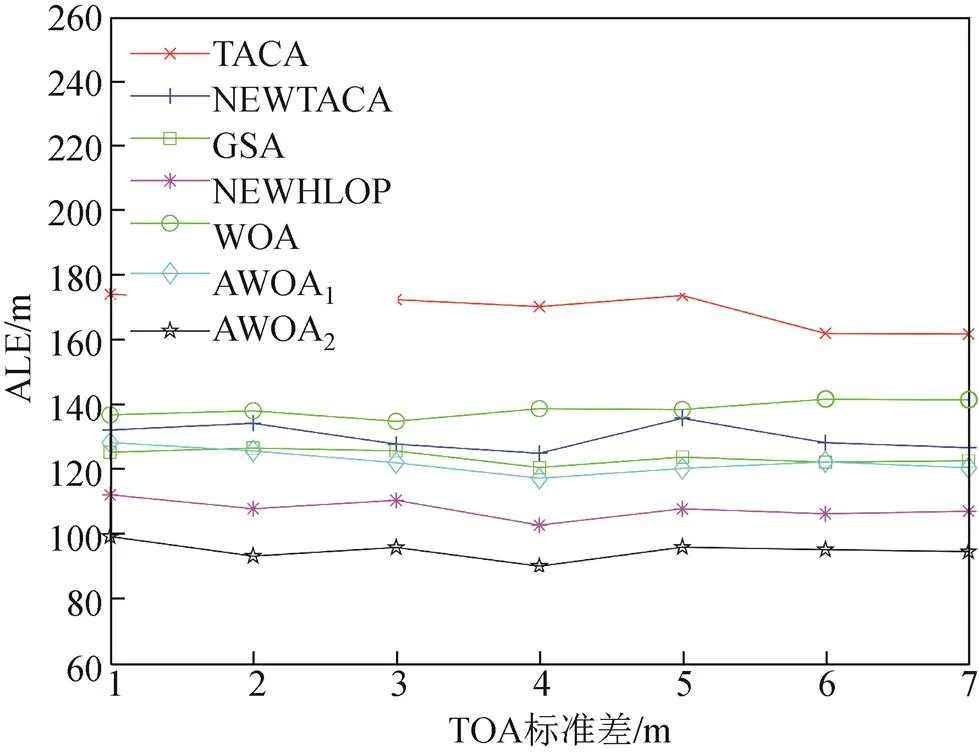
图8 ALE随距离测量误差的变化曲线

如表1所示为几种不同的定位算法在中央处理器（central processing unit，CPU）为AMD Ryzen74800U、主频为1.80 GHz的电脑上使用矩阵实验室（matrix laboratory，MATLAB）软件于同一仿真环境下进行1000次独立定位的平均消耗时间和平均定位误差。从表中可以看出，虽然本文的AWOA算法计算复杂度略高于NEWHLOP算法和GSA算法，但定位性能最佳。在传统的WOA算法基础上引入自适应动态惯性权重策略之后，AWOA2算法的平均消耗时间降低了约50%，而平均定位误差则降低了约41%，具有更好的定位性能。

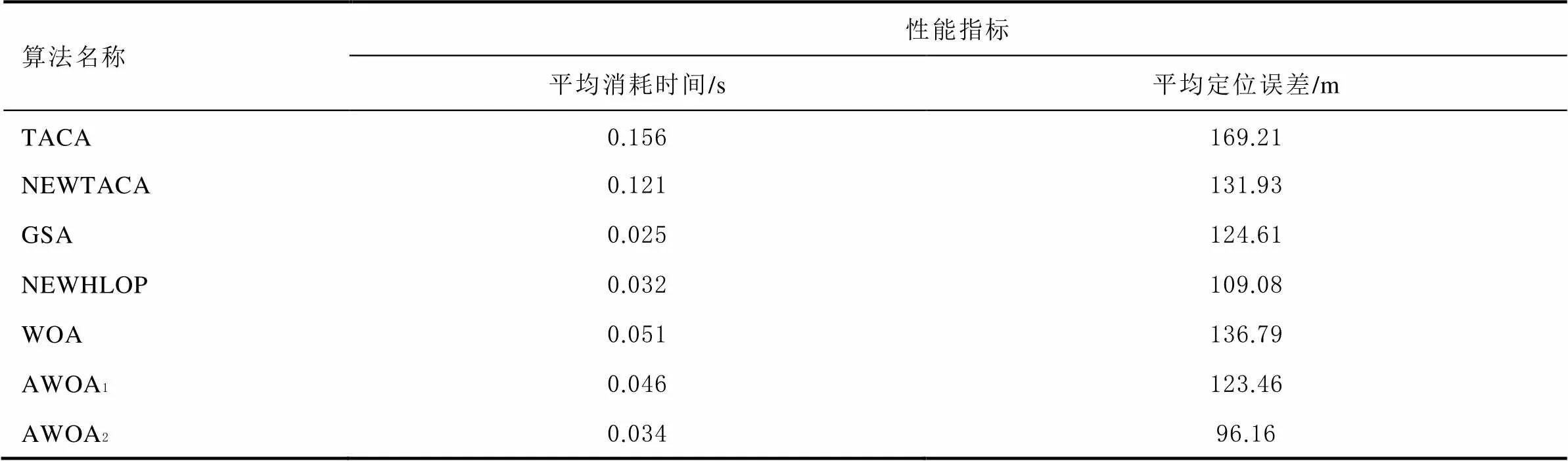
表1 算法平均消耗时间及平均定位误差

4 结束语

[1] LIU Y, WANG Y, SHEN Y, et al. Hybrid TOA-AOA WLS estimator for aircraft network decentralized cooperative localization[J]. IEEE Transactions on Vehicular Technology, 2023, 72(7): 9670-9675.

[2] VENKATRAMAN S, CAFFERY J. Hybrid TOA/AOA techniques for mobile location in non-line-of-sight environments[C]// Wireless Communications & Networking Conference. IEEE, 2004.

[3] Al-JAZZAR S, GHOGHO M, MCLERNON D. A joint TOA/AOA constrained minimization method for locating wireless devices in non-line-of-sight environment[J]. IEEE Transactions on Vehicular Technology, 2009, 58(1): 468-472.

[4] BOYD S P, VANDENBERGHE L. Convex optimization[M]. Cambridge University Press, 2004.

[5] WU S, XU D, WANG H. Joint TOA/AOA location algorithms with two BSs in circular scattering environments[J]. WSEAS Transactions on Communications, 2015, 14: 235-240.

[6] XIE Y, WANG Y, ZHU P, et al. Grid-search-based hybrid TOA/AOA location techniques for NLOS environments[J]. IEEE Communications Letters, 2009, 13(4): 254-256.

[7] GAD A G. Particle swarm optimization algorithm and its applications:A systematic review[J]. Archives of Computational Methods in Engineering, 2022, 29(5): 2531-2561.

[8] WYE K, ZAKARIA S, KAMARUDIN L M, et al. RSS-based fingerprinting localization with artificial neural network[J]. Journal of Physics:Conference Series, 2021, 1755(1): 012033.

[9] CHENG C H, WANG T P, HUANG Y F. Indoor positioning system using artificial neural network with swarm intelligence[J]. IEEE Access, 2020, 8: 84248-84257.

[10] HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris hawks optimization:Algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849-872.

[11] TAGNE F E, NYABEYE P D K, TONYE E. A new hybrid localization approach in wireless sensor networks based on particle swarm optimization and tabu search[J]. Applied Intelligence, 2022: 1-16.

[12] MIHOUBI M, RAHMOUN A, LORENZ P. Node localization in WSN and IoT using harris hawks optimization algorithm[J]. 2021 IEEE Global Communications Conference (GLOBECOM), 2021: 1-6.

[13] ERTEL R B, REED J H. Angle and time of arrival statistics for circular and elliptical scattering models[J]. IEEE Journal on Selected Areas in Communications, 1999, 17(11): 1829-1840.

[14] 邓平, 谢雪. 基于几何约束及迭代的NLOS环境定位算法[J]. 西南交通大学学报, 2021, 56(3): 666-672.

[15] GHAREHCHOPOGH F S, GHOLIZADEH H. A comprehensive survey:Whale optimization algorithm and its applications[J]. Swarm and Evolutionary Computation, 2019, 48: 1-24.

[16] 赵志刚, 林玉娇, 尹兆远. 基于自适应惯性权重的均值粒子群优化算法[J]. 计算机工程与科学, 2016, 38(3): 501-506.

[17] 董文永, 康岚兰, 刘宇航, 等. 带自适应精英扰动及惯性权重的反向粒子群优化算法[J]. 通信学报, 2016, 37(12): 1-10.

[18] 张永, 陈锋. 一种改进的鲸鱼优化算法[J]. 计算机工程, 2018, 44(3): 208-213,219.

[19] 徐刚, 杨玉群, 黄先玖. 一种非线性权重的自适应粒子群优化算法[J]. 计算机工程与应用, 2010, 46(35): 49-51.

[20] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.

A TOA/AOA optimization localization algorithm based on whale optimization

QIN Jie1, DENG Ping1, LUO Rui2, XIA Yuping1

（1. School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610097, China;2. School of Computer Science, Chengdu Normal Institute, Chengdu 611130, China）

Aiming at the problem that wireless localization algorithm based on optimization theory in non-line-of-sight (NLOS) environment is prone to fall into local optimum at the late stage of iterative operation, which leads to the degradation of localization accuracy, the paper proposed a whale-optimized time of arrival (TOA)/angle of arrival (AOA) optimal localization algorithm based on nonlinear, adaptive dynamic inertia weights: the hybrid TOA/AOA localization model based on double base stations localization scenario was built; and in the localization process, a hybrid linear localization algorithm with angle constraint condition was used to initialize the population position for avoiding the population from falling into local optimum at the early localization stage; then, when searching and updating the optimal individuals, adaptive dynamic inertia weight coefficient was introduced to improve the performance of whale optimization algorithm, in order to better coordinate and optimize the global stochastic search and local optimization-seeking capability of the algorithm. Simulational results showed that compared with existing intelligent optimization algorithms such as particle swarm optimization (PSO), whale optimization algorithm (WOA) and modified whale optimization algorithm (MWOA), the proposed algorithm would exhibit faster convergence speed and better convergence accuracy in the iterative optimization search process; moreover, compared with WOA algorithm, the average consumption time could be reduced by about 50%, the average positioning error could be reduced by about 41%, indicating a better localization performance.

whale optimization algorithm (WOA); non-line-of-sight (NLOS); intelligent optimization; wireless localization

秦杰，邓平，罗锐，等. 一种基于鲸鱼优化的TOA/AOA最优化定位算法[J]. 导航定位学报, 2023, 11(6): 93-101.（QIN Jie, DENG Ping, LUO Rui, et al. A TOA/AOA optimization localization algorithm based on whale optimization[J]. Journal of Navigation and Positioning, 2023, 11(6): 93-101.）DOI:10.16547/j.cnki.10-1096.20230612.

P228

A

2095-4999(2023)06-0093-09

2023-02-08

国家自然科学基金（61871332）。

秦杰（1995—），女，四川宜宾人，硕士研究生，研究方向为无线网络定位技术。

邓平（1964—），男，四川宜宾人，博士，教授，研究方向为无线网络定位技术、统计信号处理等。