BDSBAS-B1C服务性能评估模型分析
2023-02-23张龙平田先才
张龙平,田先才,辛 洁,原 亮,万 军
BDSBAS-B1C服务性能评估模型分析
张龙平1,2,田先才1,辛 洁3,原 亮1,万 军4
(1. 航天宏图信息技术股份有限公司,北京 100195;2. 滁州学院,安徽 滁州 239000;3. 北京卫星导航中心,北京 100094;4. 中国信息通信研究院,北京 100191)
为了进一步提高卫星导航定位精度,提出一种北斗星基增强系统(BDSBAS)服务信号BDSBAS-B1C服务性能评估模型分析方法:介绍北斗三号全球卫星导航系统(BDS-3)星基增强和国外星基增强系统发展概况;并给出星基增强卫星轨道误差、钟差误差、电离层改正误差模型,以及完好性保护水平计算模型;然后基于国际GNSS监测与评估系统(iGMAS)数据对星基增强轨道、钟差、格网电离层改正精度以及定位服务性能进行评估,构建斯坦福(Stanford)图模型来判断系统定位结果的安全等级,并计算服务区内保护水平覆盖情况。实验结果表明,卫星轨道径向(R)、切向(T)、法向(N)方向改正精度分别为0.56、1.06、0.88 m,钟差改正精度为0.95 ns;水平、高程定位精度(95%)分别为1.31、2.06 m;水平、垂直保护水平(95%)分别为5.12、8.09 m,根据Stanford图安全等级结果,能够满足国际民航组织对一类垂直引导进近(APV-I)的指标要求。
星基增强(SBAS);完好性;保护水平;电离层延迟;定位精度
0 引言
北斗星基增强系统(BeiDou satellite based augmentation system,BDSBAS)是北斗三号全球卫星导航系统(BeiDou global navigation satellite system,BDS-3)的重要组成部分,通过3颗地球静止轨道(geostationary Earth orbit,GEO)卫星——伪随机噪声识别码(pseudo random noise code,PRN)为130、143、144——并分别在B1C与B2a信号上向中国及周边用户播发全球定位系统(GPS)卫星星历误差、卫星钟差、电离层延迟以及完好性等多种增强信息,旨在提供符合国际民航组织(International Civil Aviation Organization,ICAO)标准的单频(single frequency,SF)服务和双频多星座(dual frequency multiple constellation,DFMC)服务[1-3]。
目前,国外具备星基增强服务能力的有美国的广域增强系统(wide area augmentation system,WAAS)、欧洲的地球静止轨道卫星导航增强服务系统(European geostationary navigation overlay service,EGNOS)、俄罗斯的差分校正和监测系统(system of differential correction and monitoring,SDCM)、日本的多功能卫星增强系统(multi-functional satellite augmentation system,MSAS),以及印度的GPS辅助GEO增强导航系统(GPS aided GEO augmented navigation,GAGAN)等,这些星基增强系统都已经通过当地民航机构认证[4-6]。2020年11月,BDS国际民航组织标准完成全部技术验证,距离BDS正式写入国际民航组织标准更进了一步。
星基增强最初目标是为民用航空导航服务提供完好性保证,同时提高卫星导航定位精度。将全球卫星导航系统(global navigation satellite syste,GNSS)观测量的星历误差、钟差误差、电离层误差等进行划分,并对每一项误差源进行模型化计算,然后将计算出来的误差修正值通过GEO卫星播发给用户,用户基于广播电文和改正信息对各项误差进行修正,以达到削弱误差并改善定位精度的目的[7-8]。对于完好性方面,GPS系统导航电文中具备一定程度的完好性监测,但通常需1 h,不能满足民航完好性6 s告警的需求。为了保证民航对导航安全的要求,通过星基增强系统提供的完好性信息可以有效解决告警时间较长的问题[9-12]。
2020年7月,北斗卫星导航系统发布了《北斗卫星导航系统空间信号接口控制文件-星基增强服务信号BDSBAS-B1C》。基于该接口控制文件,本文对BDSBAS-B1C计算评估模型进行研究,主要从卫星轨道、钟差、电离层延迟、定位精度,以及完好性保护水平等方面进行分析和实验,并得到初步评估结果。
1 BDSBAS-B1C服务相关模型
1.1 误差改正模型
卫星导航信号从发射到接收会受到各类误差的影响,主要包含卫星端的星历、星钟误差,信号传播过程中的电离层、对流层延迟误差,以及设备端的多路径、接收机噪声等误差。BDSBAS在电文2~5、25、28中播发了星历与星钟等相关改正误差,在电文18、26中播发了电离层延迟改正信息,可以综合分为快变改正、慢变改正以及电离层延迟改正[13-15]。
1)快变改正。快变改正数包含钟差快变改正数与伪距快变改正数,定位中要把伪距快变改正数加入到原始伪距中。
伪距快变改正数为
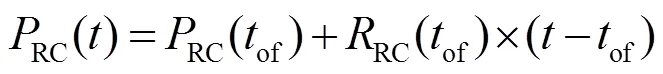
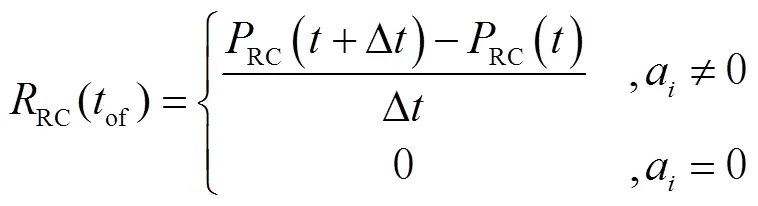
钟差快变改正数为
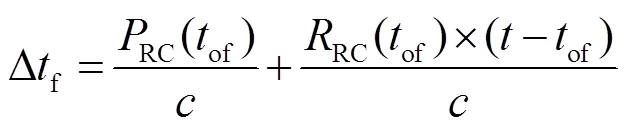
式中为光速。


钟差慢变改正数为
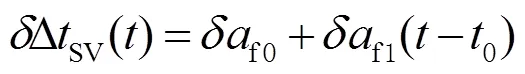
3)电离层延迟改正。BDSBAS-B1C通过电文18、26播发服务区内电离层格网点垂直延迟改正值,电文18主要包括电离层格网掩码信息,电文26包括电离层格网点垂直延迟值。为了得到用户位置处的电离层延迟改正值,需要进行如下计算过程[16-18]:
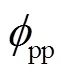
第二步:格网点选择,计算完穿刺点经纬度后,根据电文18中的信息确定使用的电离层格网点。
第三步:穿刺点电离层垂直延迟解算,根据周围的格网点来内插计算穿刺点处的电离层延迟。
第四步:穿刺点电离层改正数解算,根据电离层垂直延迟值与倾斜因子计算电离层倾斜延迟。
1.2 定位解算模型
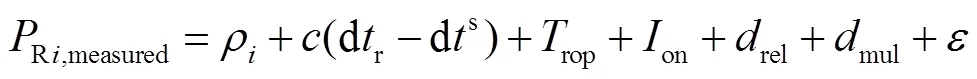

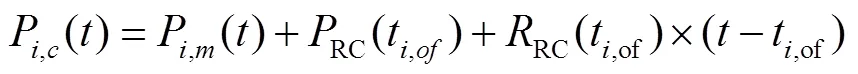
星基增强通常采用最小二乘进行伪距单点定位,将式(7)进行线性化处理即可[19-20]。
1.3 完好性保护水平计算模型
完好性是指当卫星导航系统发生故障时,在规定时间内向用户提供及时且有效告警的能力。通常,描述完好性的指标参数有完好性风险、告警时间、告警限值以及保护水平,其中,保护水平分为水平保护水平(horizontal protection level,HPL)与垂直保护水平(vertical protection level,VPL)。对于不同飞行阶段的航空器,保护水平的计算方法为[12,21]

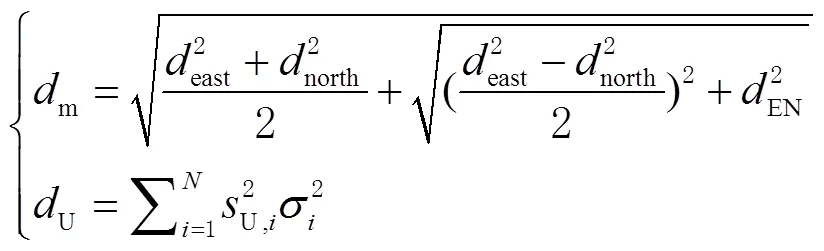
其中
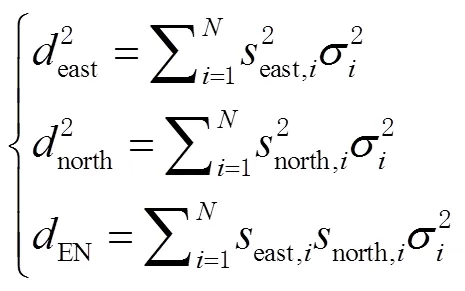
投影矩阵的计算方法为
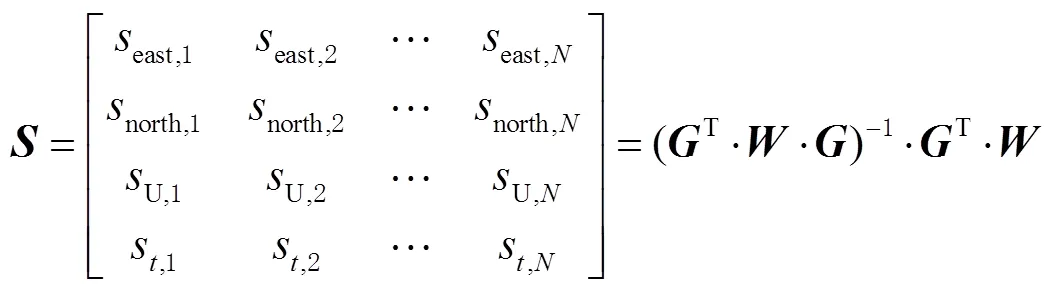
HPL和VPL分别与水平告警限值(horizontal alarm limit,HAL)和垂直告警限值(vertical alarm limit,VAL),以及水平定位误差(horizontal positioning error,HPE)和高程定位误差(height positioning error,VPE)相互比较,判断发生告警的事件类型,告警事件分为“危险错误引导信息(hazardously misleading information,HMI)”“错误引导信息(misleading information,MI)”,以及“系统不可用”。
2 实验与结果分析
本文所有实验使用的是2022年年积日第266—295天的观测数据与广播星历。因为提供北斗三号星基增强服务的3颗GEO卫星播发的增强信息一致,因此以PRN130卫星播发的电文数据进行处理。
2.1 卫星轨道、钟差改正精度
该实验根据广播星历及星基增强相关电文信息,按照5 min采样间隔计算每颗卫星改正后的卫星轨道与钟差,然后和国际GNSS监测与评估系统(international GNSS monitoring and assessment system,iGMAS)提供的精密轨道、钟差产品进行比较,给出每颗卫星轨道(径向(radial,R)切向(tangent,T)法向(normal,N))、钟差改正精度均方根(root mean square,RMS)统计结果,如图1、图2所示,图中PRN为伪随机噪声识别码(pseudo random noise code)。
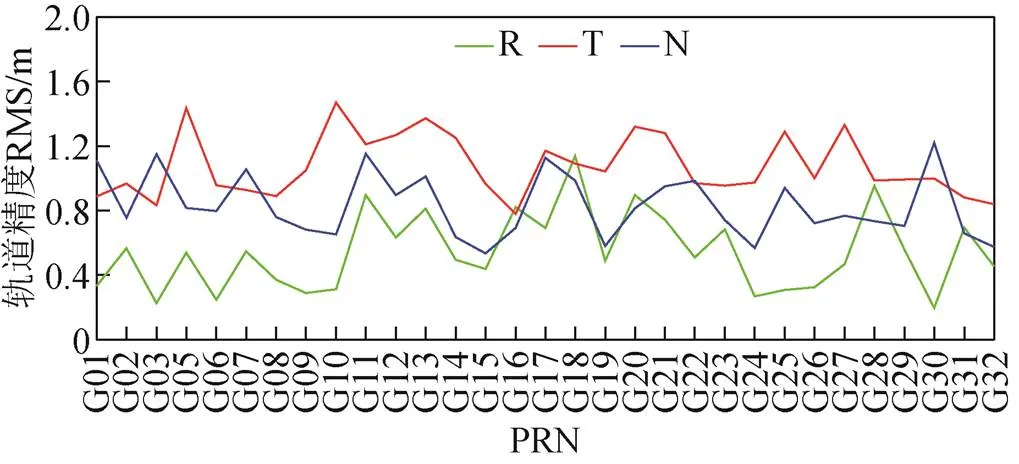
图1 各卫星轨道改正精度
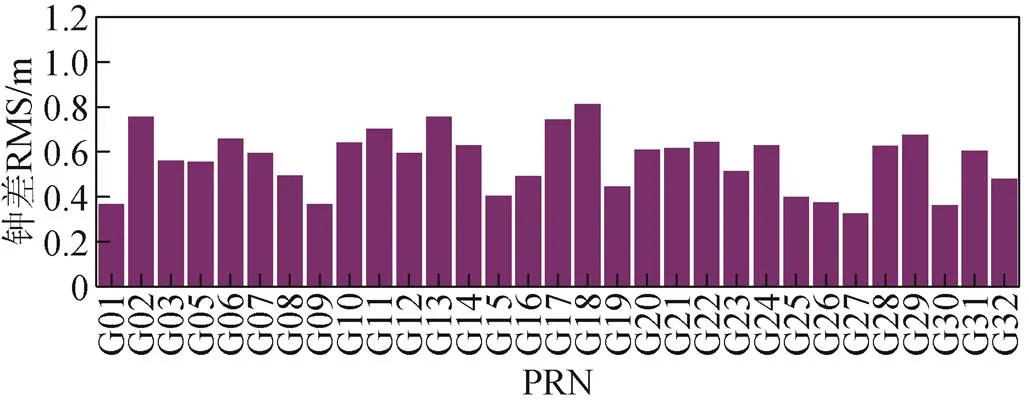
图2 各卫星钟差改正精度
以G01卫星为例,给出30 d轨道与钟差改正序列,如图3所示。
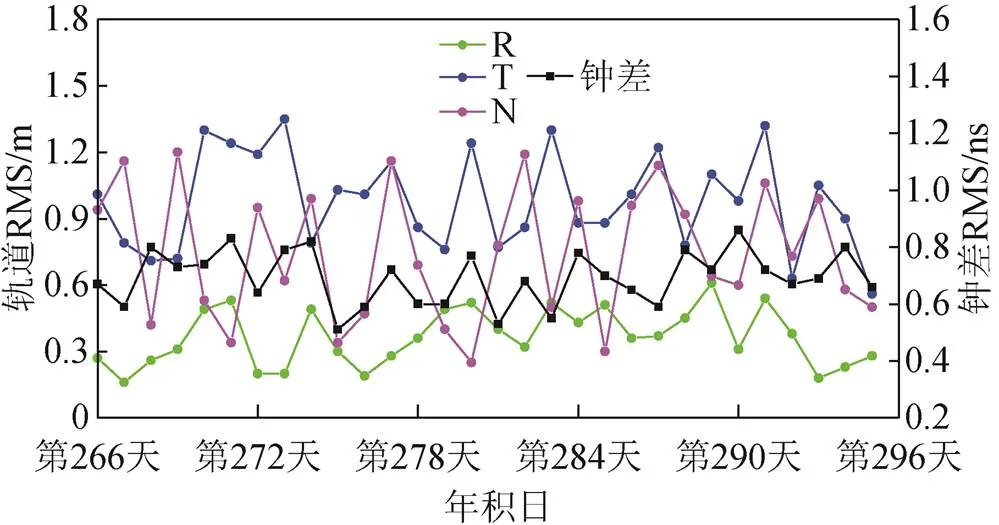
图3 G01卫星30 d轨道精度、钟差改正序列
如表1所示为每颗卫星轨道(R、T、N)、钟差改正精度统计结果。
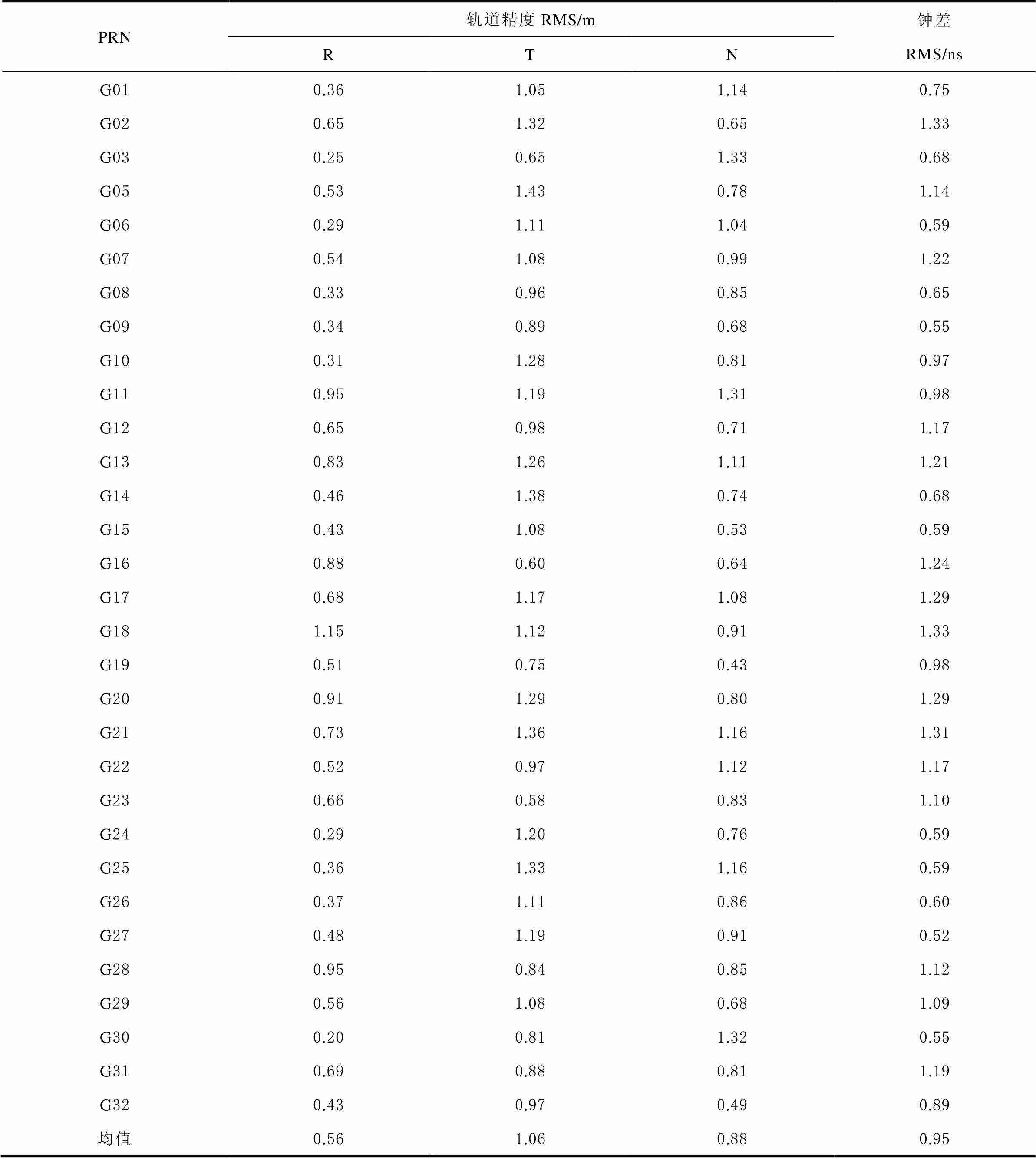
表1 各卫星轨道、钟差改正精度
综合图1、图2和表1可以看出,卫星在R、T、N各方向上的轨道改正精度均值分别为0.56、1.06、0.88 m,卫星钟差改正精度均值为0.95 ns。
2.2 电离层延迟改正精度
为了满足BDSBAS格网电离层与最终精密电离层产品之间的一致性,对中国及周边区域划分成1°×1°的格网,并将根据BDSBAS-B1C计算出的电离层延迟量与最终精密电离层延迟量作差,计算出每个格网点电离层延迟改正精度。
中国绝大数地区的电离层延迟改正精度在0.3 m以上,部分区域在0.4 m左右;在电离层活跃较为剧烈的下午,低纬度地区及部分中高维度地区电离层延迟改正精度较差,整体在0.5 m左右。
2.3 服务性能
基于分布于中国北京、上海、武汉、西安、昆明5个站的观测数据进行BDSBAS-B1C服务性能评估实验,实验内容主要包括定位性能与保护水平。如图4、图5所示为北京站年积日第266天 1 d(采样间隔为30 s)的各方向定位序列、位置精度衰减因子(position dilution of precision,PDOP)值,以及可见卫星数。

图4 定位误差
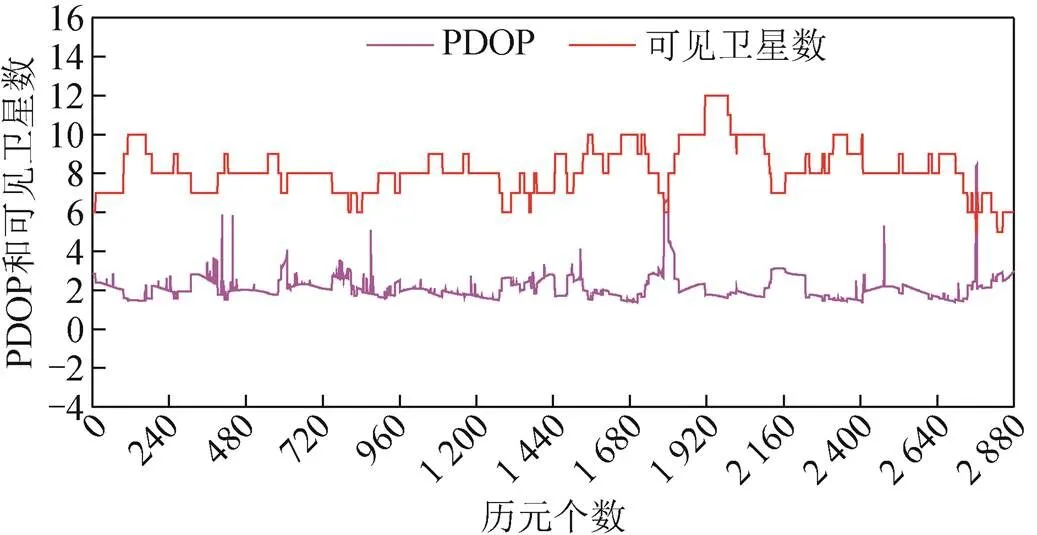
图5 PDOP和可见卫星数
为了进一步评估BDSBAS-B1C的定位精度,对上述5个站单天基本导航与星基增强定位精度(95%)进行统计,并计算30 d的均值,如表2所示。
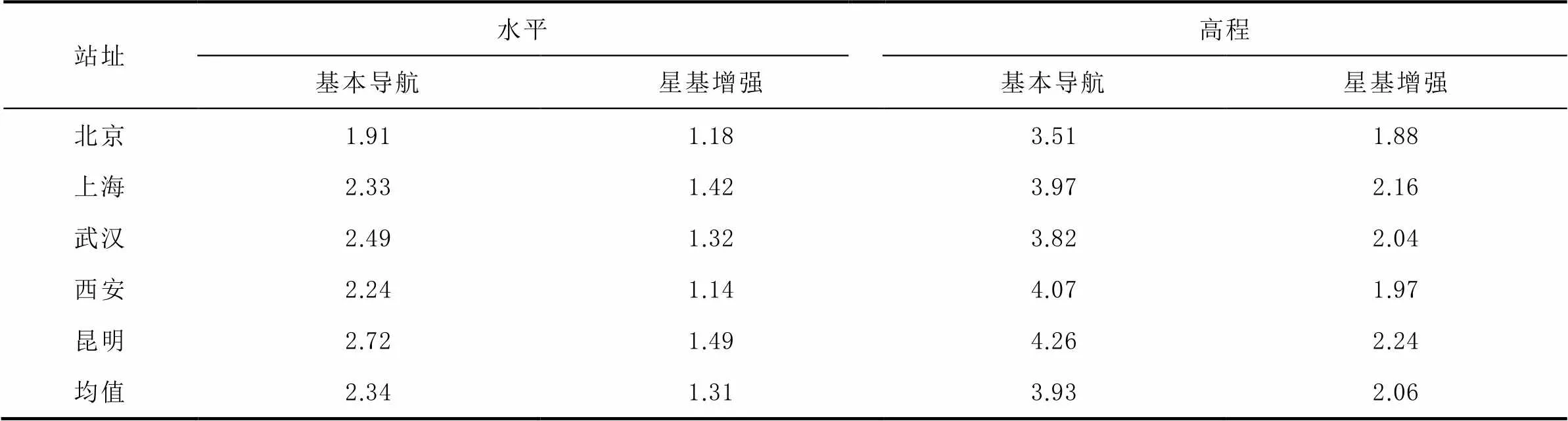
表2 各站定位精度统计结果 m
由图4、图5可以看出,可见卫星数、PDOP大部分时间在6颗、2.0左右。由表2可以看出,星基增强服务的水平、高程定位精度分别为1.31、2.06 m,相较于基本导航定位精度分别提升了43.9%、47.6%。
根据国际民航组织对一类垂直引导进近(APV-I)的要求,水平和高程定位精度限值分别为16、20 m,水平和垂直告警限值分别为40、 50 m。如图6、图7所示分别为北京站在年积日第266天1 d(采样间隔为30 s)的各方向定位精度、保护水平与告警限值序列。
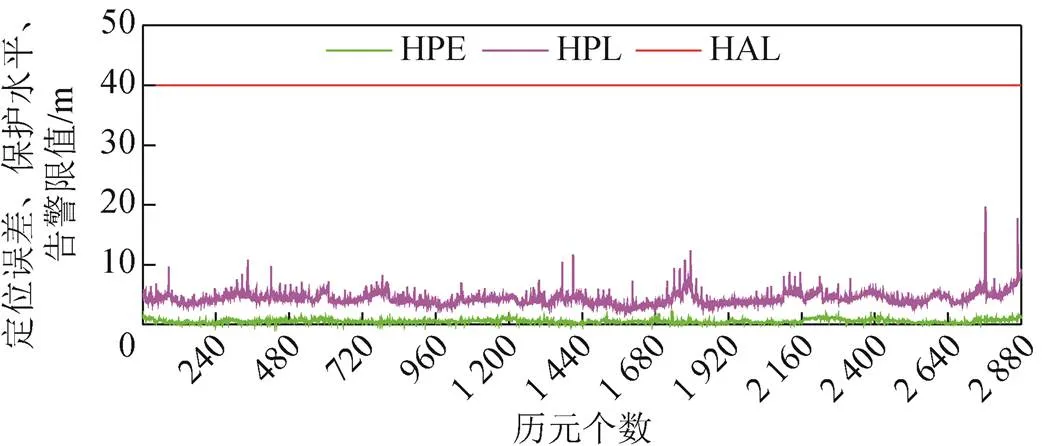
图6 水平方向序列

图7 垂直方向序列
由图6、图7可以看出,水平与垂直保护水平分别在5.12、8.09 m左右,均未超出告警限值。对中国及周边地区水平、垂直保护水平分布情况分析,在中国境内绝大部分地区,水平保护水平在 5 m以内,垂直保护水平在10 m以内。
通过前文可知,定位精度、保护水平及告警限值相互比较后,可以得到不同的完好性事件,对于“HMI”“MI”和“系统不可用”之间的关系,构建斯坦福(Stanford)图模型来表征。Stanford图可用来快速检核系统的完好性状态,只须确认采样点是否落在Stanford图的对角线轴的上方即可,同时也可采用Stanford图来判断定位结果的安全等级。如图8、图9所示分别为北京站86400个历元(30 d,采样间隔为30 s)在水平、垂直方向上的Stanford图。
在图8、图9中,横轴代表定位误差,纵轴代表保护水平,其他各部分代表发生不同告警的概率。由图中可以看出,从对北京站观测的86400个历元数据来看,各方向系统“可用”概率均为100%。
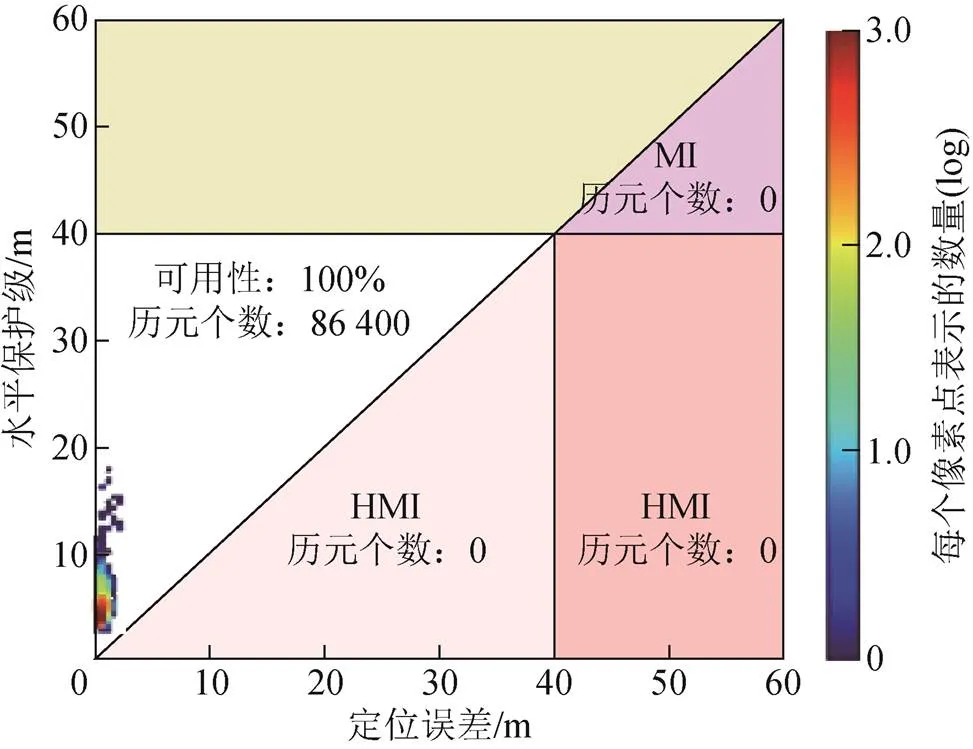
图8 水平方向Stanford图
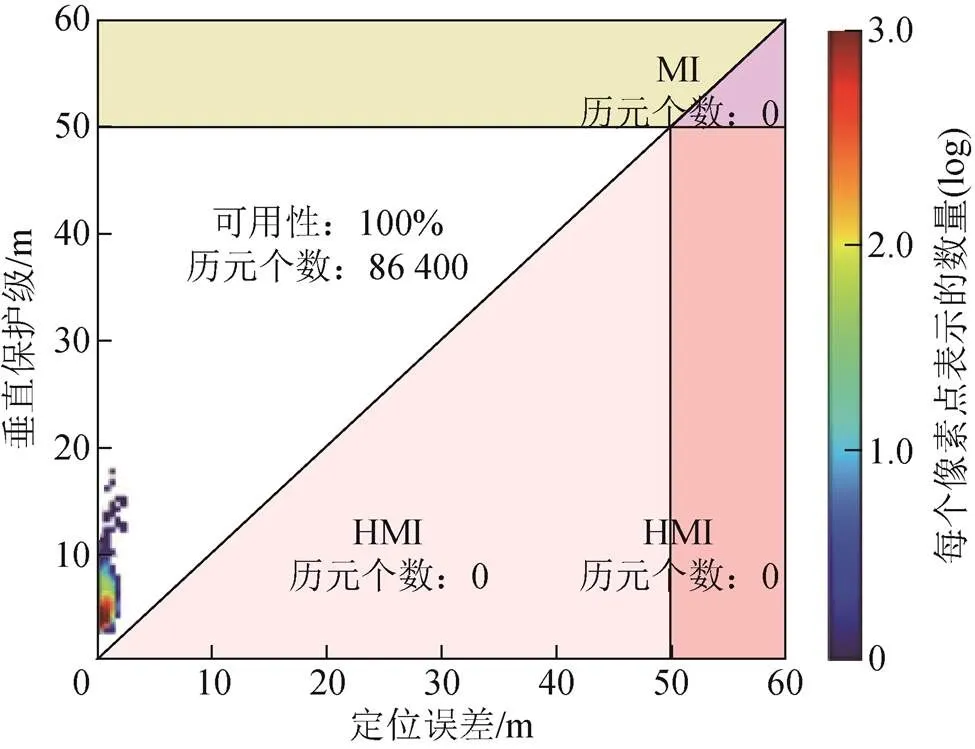
图9 垂直方向Stanford图
3 结束语
本文采集了北斗三号PRN130卫星播发的星基增强数据,对卫星轨道、钟差误差以及电离层延迟改正精度进行了评估,并对分布在中国境内5个iGMAS站点进行了定位精度与保护水平等服务性能的评估,具体评估结果如下:
1)给出了BDSBAS-B1C轨道、钟差、电离层改正模型,以及定位、完好性保护水平计算方法,并进行了实验分析。
2)从30 d的数据统计结果来看,卫星轨道R、T、N方向改正精度分别为0.56、1.06、0.88 m,卫星钟差改正精度为0.95 ns。
3)对于电离层改正效果,在中国绝大多数地区均能实现优于0.4 m的水平,在低纬度及电离层活跃时候能实现0.5 m的精度。
4)服务性能方面,30 d所有评估的站点在水平和高程方向上的平均精度分别为1.31、2.06 m,保护水平可以满足国际民航组织对一类垂直引导进近(APV-I)的指标要求。
致谢:感谢国际GNSS监测与评估系统(iGMAS)提供的数据。
[1] 北斗卫星导航系统空间信号接口控制文件(星基增强服务信号BDSBAS-B1C)[Z]. 北京: 中国卫星导航系统管理办公室, 2020.
[2] 杨元喜,许扬胤,李金龙,等.北斗三号系统进展及性能预测——试验验证数据分析[J].中国科学:地球科学,2018,48(5):584-594.
[3] 杨长风.中国北斗导航系统综合定位导航授时体系发展构想[J].中国科技产业,2018(6):32-35.
[4] SHERIDAN K, DYJAS T, BOTTERON C, et al. Demands of the road:An assisted-GNSS solution uses the EGNOS data access service[J]. GPS World, 2011.
[5] STAPLETON D P. Global positioning system/Wide area augmentation system (GPS/WAAS) final approach error analysis[J]. 2002.
[6] AUTHIÉ T, TRILLES S, FORT J C, et al. Integrity based on MT28 for EGNOS:New algorithm formulation & results[C]// The 30th International Technical Meeting of the Institute of Navigation. Portland, Oregon, USA, 2017.
[7] ENGE P, KALAFUS R. Differential operation of the global positioning system[J]. IEEE Communications Magazine:Articles, News and Events of Interest to Communications Engineers, 1988, 26(7): 48-60.
[8] GRZEGORZEWSKI M, KAROL KRZYSZTOF Ś. The GNSS system application in the LPV-200 landing approach procedure. Part I:Approach to practical verification[J]. Annual of Navigation, 2016, 23(1): 251-258.
[9] PIETER B O, DAVIDE I, SANDRA V, et al. Empirical integrity verification of gnss and sbas based on the extreme value theory[J]. Navigation, 2014, 61(1): 23-38.
[10] 刘瑞华,席泽谱,吕吉方.BDSBAS完好性保护级分析与研究[J].航天控制,2020,38(4):28-33.
[11] 杨晓义,李锐,黄智刚.BDS星座的完好性保护级改进算法[J].导航定位学报,2016,4(2):67-70, 80.
[12] JIN B, CHEN S, LI D, et al. Performance analysis of SBAS ephemeris corrections and integrity algorithms in China region[J]. Satellite Navigation, 2021, 2(1): 1-14.
[13] 张龙平,党亚民,谷守周,等.北斗卫星导航系统实时定轨及SSR改正信息生成方法[J].测绘通报,2017(12):1-5.
[14] 刘瑞宁,李建文,郭亮亮,等.GPS广播星历轨道误差分布模型探讨[J].导航定位学报,2018,6(2):46-52.
[15] HEΒELBARTH A, WANNINGER L. SBAS orbit and satellite clock corrections for precise point positioning[J]. GPS Solutions, 2013, 17(4): 465-473.
[16] SHIVELY C A. Analysis of specified and hypothetical GPS IIIC integrity for LPV 200 operations[J]. Proceedings of the International Technical Meeting of the Institute of Navigation Itm, 2010, 3(4): 975-986.
[17] BAO J, LI R P, et al. Impact of ionospheric irregularity on sbas integrity:Spatial threat modeling and improvement[J]. Journal of Systems Engineering and Electronics, 2018, 29(5): 908-917.
[18] 丁毅涛,郭美军,范顺西,等.广播电离层模型精度评估分析[J].导航定位学报,2022,10(1):53-63.
[19] MONTSERRAT V P. Archivo general universitat politécnica de catalunya[J]. Boletín de la ANABAD, 1997, 47(3): 163-168.
[20] YANG Y, DING Q, GAO W, et al. Principle and performance of BDSBAS and PPP-B2b of BDS-3[J]. Satellite Navigation, 2022, 3(1): 1-9.
[21] RIPPL M, DIAZ S P, SCHLÜTER S, et al. Global integrity combining ARAIM and SBAS method and operational benefit[C]// ION GNSS+ 2018. 2018.
Analysis on BDSBAS-B1C service performance evaluation models
ZHANG Longping1,2, TIAN Xiancai1, XIN Jie3, YUAN Liang1, WAN Jun4
(1. Piesat Information Technology Co., Ltd., Beijing 100195, China; 2. Chuzhou University, Chuzhou, Anhui 239000, China; 3. Beijing Satellite Navigation Center, Beijing 100094, China; 4. China Academy of Information and Communications Technology, Beijing 100191, China)
In order to further improve the positioning accuracy of satellite navigation, the paper proposed an analysis method on BeiDou satellite based augmentation system (BDSBAS)-B1C service performance evaluation model: the development of BDSBAS and other satellite based augmentation system (SBAS)system was introduced, and the error correction and integrity calculation models of SBAS were given, including models of satellite orbit error, clock error, ionospheric correction and integrity protection level calculation; then, the orbit, clock error, grid ionospheric correction accuracy and positioning accuracy of SBAS were evaluated based on the iGMAS data; at the same time, the Stanford graph model was constructed to judge the security level of the system’s positioning results, and the protection level coverage in the service area was calculated finally. Experimental results showed that the satellite orbit correction accuracy in radial (R), tangent (T) and normal (N) directions would be 0.56, 1.06 and 0.88 m, respectively, and the clock error correction accuracy would be 0.95 ns; meanwhile, the horizontal and elevation positioning accuracy (95%) would be 1.31 and 2.06 m, respectively, and the horizontal protection level and vertical protection level (95%) would be 5.12 and 8.09 m, respectively, which could fully meet the requirements of International Civil Aviation Organization (ICAO) for APV-I according to the safety level results of Stanford diagrams.
satellite based augmentation system (SBAS); integrity; protection level; ionospheric delay; positioning accuracy
张龙平,田先才,辛洁,等. BDSBAS-B1C服务性能评估模型分析[J]. 导航定位学报, 2023, 11(6): 149-155.(ZHANG Longping, TIAN Xiancai, XIN Jie, et al. Analysis on BDSBAS-B1C service performance evaluation models[J]. Journal of Navigation and Positioning, 2023, 11(6): 149-155.)DOI:10.16547/j.cnki.10-1096.20230618.
P228
A
2095-4999(2023)06-0149-07
2022-12-05
张龙平(1988—),男,山东莱州人,博士,高级工程师,研究方向为北斗卫星导航系统高精度位置服务。
