一种面向医疗人力资源应急调度的优化算法设计

赵宏业

（河北北方学院附属第二医院，河北张家口 075100）

新冠疫情事件的出现不仅危害国民的生命健康，同样也对生产活动造成了巨大影响。就本质而言，这类紧急卫生事件的应对需要依靠国家应急治理体系与治理能力。但在疫情初期，由于医疗人力资源的分配和调度均较为迟缓，且资源分配不合理导致了较高的病死率。因此，解决医疗人力资源分配的问题，对应急公共事件的治理能力会有较大提升[1-3]。

人力资源分配从本质上看是任务分配与指派的问题，抽象成数学模型即数据的组合及权重优化问题。其目的是将该类资源合理地分配给多个使用者，从而使资源能够尽可能达到最大化的使用效果[4]。与此同时，人力资源分配也是国内外学者的研究热点。常见的算法均为通过权重法将多目标的人力资源分配模型简化成单目标的人力资源优化模型。如文献[5]中提到的基于遗传算法的人力资源分配算法，其考虑了班次与上班时间段这两种因素，并建立了单目标优化模型。但该方法具有一定的局限性，在求解时无法包含全部的最优解。故该文使用粒子群算法对目标进行优化，且最终得到了准确的结果。

1 医疗人力资源调度算法设计

1.1 人力资源配置模型

医疗人力资源的优化调度可抽象为医疗车到达救助点的时间问题。在这一过程中，运输成本、救助效果、救助点及人力数量均会成为影响分配效果的因素。

针对上述人力资源的分配问题，首先存在以下定义：任务序号为i(i=1,2,…,I)，其中，I为任务的总数量；j表示医疗人力序号，且j=1,2,…,J,J为总的医务人员数量；cij表示将医疗人力运输至救助点需要花费的成本；eij表示将j个医疗人力运输至第i个任务点所取得的救助效果；xij为决策变量，如式（1）所示：

由此，可以建立式（2）-（5）所示的约束函数:

其中，式（2）表示效果最大化函数，且A为其最大值；式（3）表示所花费成本最小化函数，且B为其最小值；而式（4）表示人力资源约束；式（5）则表示救助点任务约束。

1.2 多目标粒子群算法

粒子群算法（Particle Swarm Optimization,PSO）是一种模拟鸟群觅食过程的智能仿真算法[6-10]。该算法假设搜索时的空间矩阵为D维，且每个维度的粒子群个数为n。而粒子群中的每个粒子均会发生进化，该进化过程是寻找自身的最优解对其当前位置进行更新。通常进化过程存在两个方面：一个是粒子本身寻找到最优解；另一个则是整个群体找到最优解。粒子群算法的执行过程如图1 所示。

图1 粒子群算法执行过程

粒子进化的速度以及位置公式如下：

式（6）表示粒子更新的速度，其中，t为时间自变量，p为更新概率。式（7）表示粒子更新的位置。其中，c1、c2为学习因子，ω为惯性因子，r为随机数，α为约束因子。

多目标粒子群优化算法（Multi-Objective Particle Swarm Optimization,MOPSO）是对基础粒子群算法的改进，其基本的算法原理：在对种群进行初始化后，将初始的种群大小记为n。基于适应度支配的思想，将初始种群切割为两个子种群。而子种群又分为可支配和不可支配子集合，其集合的元素数量分别为n1与n2，且n1+n2=n。

在多目标粒子群的迭代过程中，仅对非支配子集中的元素加以更新，同时对更新完毕的粒子进行适应度比较。该算法的详细执行过程如图2 所示。

图2 算法执行过程

算法的关键数据处理步骤有：

1）初始化

初始化种群，种群中的元素如下，且数组的维数为d。

2）适应度确定

计算种群的适应度，公式如下：

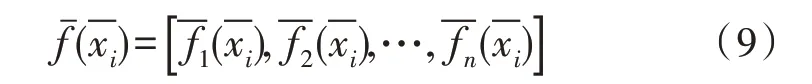
3）速度和位置更新

对非支配子集中粒子的速度及位置进行更新如下：

4）动态交换及比较

比较非支配子集合与可支配子集中的粒子，若非支配子集合中的粒子适应度小于可支配子集中的粒子，则对这两种粒子进行调换，同时更新每种粒子在集合中的序号及位置。

5）迭代次数确定

若迭代次数最大或元素全部遍历完成，则程序结束；否则更新速度和位置后再次执行程序，直至满足结束条件。

1.3 正交初始化粒子群

由上文可看出，粒子群算法作为迭代算法，粒子初始化的位置对后续算法中粒子的进化有着较为直接的影响[11-13]。若初始化种群的位置偏离最终最优解较远，则粒子无论进化多少次，最终的结果均不会准确。因此在初始化粒子时，需对粒子进行均匀化正交处理，这样可以保证所有粒子都均匀地分布在解空间几何中。

初始化策略通常使用分布指标与收敛性指标进行评估，二者计算如下：

式中，M为粒子总数；N为算法正常解的个数；d表示每个解与真实解之间的距离；γ为收敛性指标，其值越小越好；此外，Δ 越小表示解的分布性越好。

在粒子群的初始设计中，可将n个粒子集合作为一个整体粒子。但首先要将这些粒子进行离散化处理，具体如下所示：

其中，第j类、第i个正常离散粒子的初始值为li；ui为离散约束极值；Q为离散分类数。

该文产生初始化粒子的算法流程为：

1）将算法的正常解空间进行切割，形成多个子空间。

2）利用式（14）对数据进行离散化处理，并使用正交表来生成个体。

3）从对应子空间中进行抓取并选出最优的分布个体，再将其加以组合，则该组合即为初始种群。

2 算法测试及案例分析

2.1 算法测试

首先对算法进行性能测试，该测试包括算法运行最优值测试与时间测试。

对比算法选择线性粒子群算法(Linear Particle Swarm Optimization,LPSO)及粒子群算法。三种对比算法运行次数为50 次，最终取平均值作为结果。验证函数使用Sphere、Griewank、Ackley、Rosen 和Rastrigrin 五种经典对比函数。算法运行结束的标志即找到最优值或迭代次数大于200 次。最优值的计算结果如表1 所示。

表1 最优值计算结果

由最优值计算结果可以看出，该文算法最优值均小于对比算法，说明该算法性能较优。

而在计算迭代次数方面，以Sphere 函数为实例，计算迭代次数为200 时算法的收敛情况。为了便于观察指标的变化情况，故选取适应度的对数进行观察，函数的迭代次数与其对应的关系如图3 所示。

图3 适应度的对数与迭代次数关系曲线

2.2 案例分析

以2020 年新冠病毒肺炎疫情中心地武汉市为例，进行算例测试。该文将武汉铁路运送枢纽作为医疗人力资源中心配送点，以武汉市收纳病例的医院作为救助点。救助点的资源需求量可根据SEIR模型[14-16]得出，而人口数量则通过普查数据获得。

要验证算法的效果，首先应对定点医院的需求度进行分析。即医院收纳的病人越多，其需求度便越大，具体数据如表2 所示。

表2 武汉市定点医院需求度

当设置粒子群算法存在多个目标时，通常难以达到最优值结果，因此使用损失度对方案的合理性进行判断。该方案设置两个指标，分别是运输成本最小与救助率最高，并最终根据指标的不同值确定了五种方案。假定目标运输成本最小与救助率最高分别用C1和C2表示，运输损失度计算结果如表3 所示。

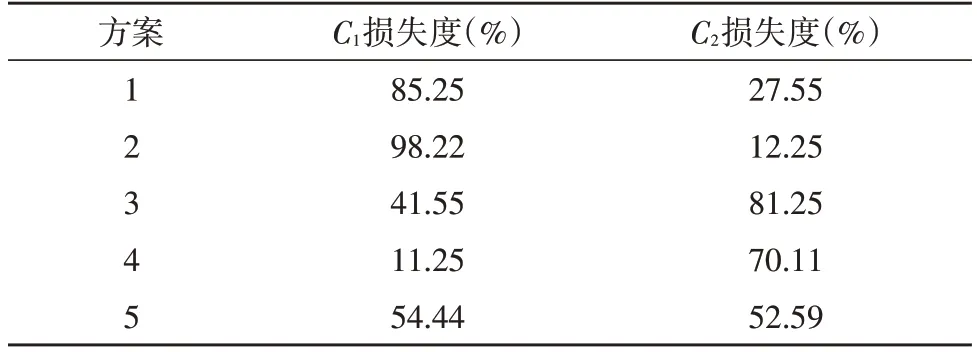
表3 运输损失度计算结果

由表3 可知，方案5 的目标损失度较为折中，因此选用该方案为最终的配送结果。

按照该文所提算法的计算结果，最终配送人力资源的具体情况如表4 所示。由此可见，该文算法能够对运送至交通枢纽的医疗人力资源进行合理分配，且具有一定的实用价值。

表4 配送人力资源百分比

3 结束语

新冠肺炎疫情等类似突发公共卫生事件的出现，不仅会危害国民的生命安全，同样也会对社会生产活动造成一定影响。合理解决医疗人力资源的分配问题，将对公共事件的应急治理能力有较大提升。该文深入分析了多目标粒子群算法，并将其应用于医疗人力资源的优化分配，通过粒子适应度对比求得最优值。同时，使用正交方法初始化粒子群，从而保证解的收敛性。性能测试实验结果显示，该算法在准确率和迭代次数方面均优于其他算法。而在实例测试中，该文算法不仅可给出多个方案，且最优方案还能兼顾多个目标，并得到最优的人力资源分配比，表明了所提算法具有一定的实用意义。