基于RSA 算法特性的安全性研究

唐 蓉，周瑜平，叶小莺，戴辛玥

（1.重庆市疾病预防控制中心科技信息处，重庆 400042；2.广东东软学院计算机学院，广东佛山 528225）

科技进步改变了人们的生活，使人们对通信网络的依赖越来越强。通信网络极大地缩短了沟通距离，也大幅提升了信息沟通的便捷性。然而，这种便捷性也衍生了一系列安全性问題，刘俊杰等[1]认为随着无线通信的快速发展和普及，通信的安全问题成为该领域的研究重点。季佳华等[2]认为对通信网络信息进行加密操作可以更好地防范网络入侵和攻击。以传染病防控领域为例，随着我国各地智慧化预警多点触发机制和多渠道监测预警机制的建立，此类信息系统包含了大量的隐私数据、敏感信息的应用场景，并由原来的医疗机构及管理部门转向科学研究、互联互通、数据汇聚、移动应用等领域，扩大了个人隐私信息类型、分布场景及泄露渠道[3]，给现行加密系统带来较大挑战，亟需更加可靠的技术手段实现健康数据的安全和保密[4-5]。RSA 算法作为当前非对称密码领域最为重要的算法之一，其安全性基础与极大整数做因数分解的难度密切相关[6]，被ISO 推荐为公钥数据加密标准，广泛应用于医疗健康[7]、电子商务[8-9]、金融[10]、公共服务[11-12]等领域。其因易于理解和操作，能同时用于加密和数字签名，被普遍认为是最优秀的公钥方案之一。但是，随着硬件、软件技术的进步和计算能力的大幅提升，RSA 算法真如大家所说的那样安全吗？是否隐藏着潜在风险？基于此，该文从RSA 算法特性研究视角出发，探讨了RSA 算法的安全性问题。

1 RSA算法回顾

在RSA 算法[13-14]中，要求任意选择两个不同的质数p和q，然后构成一个合成数n，这个合成数就是p与q的乘积。当给定一个合成数后，验证特定质数是否是该合成数的因数是轻而易举的，然而如何将该合成数分解成特定的因数，则是一个非常困难的问题。随着质数的增大，质数的乘积也随之增大，同时分解该合成数为质数的难度也增加。从理论和实践证明，将大数分解为因数的方法通常都需要指数级时间。但是，当前计算机技术的高速发展，对不少加密系统造成了较大威胁，另一方面在数学研究领域所取得的突破，越来越多的密码分析工具相继问世，无疑对信息安全的防护更是雪上加霜。

作为非对称公开加密体制的代表，该文研究证实，RSA 算法存在一定缺陷，对于RSA 系统的解密过程，解密密钥实际上是冗余的。简而言之，加密和解密过程只需要加密密钥来完成，而不是单独一组不同的加密密钥和解密密钥。基于此问题，该系统明显不符合非对称密钥体制的基本要求；且只由加密密钥即可完成加密、解密过程，而加密密钥又是公开的，这样将破坏整个系统的可靠性与安全性。另外，系统公开加密算法解密密钥原理是唯一的，该研究指出RSA 系统也不符合了这一基本要求。非线性特性要求，任意一个公开加密算法系统需要构建在非线性变换的基础上，意味着除了加、解密的过程需要是非线性外，对相应变换结果也需要达到非线性要求。虽然RSA 使用了大质数运算，整体效果是非线性的，实际上对于单一的加密算法具有线性特征。

1.1 RSA加密与解密算法的步骤

RSA 算法流程描述如下：

步骤1：首先产生两个大质数p及q，建议p或q的长度至少为1 024 比特以上。

步骤2：计算n=pq，公开参数n，不可公开p及q。

步骤3：计算欧拉函数φ(n)=(p-1)(q-1)。

步骤4：随机选择一个整数e，需滿足条件(e,φ(n))=1。

步骤5：求得整数d，使：

整数d存在，因此e与φ(n)互质。

步骤6：公布n和e，但是d需要保密。

只要n足够大，即使已知n和e，却很难从中得知p和q，因此d就无法逆推得到。

加密阶段：

解密阶段：

1.2 RSA算法的证明

1）若(m,n)=1，则(m,p)=1 且(m,q)=1，由步骤4 和步骤5 计算，存在一个整数b，使

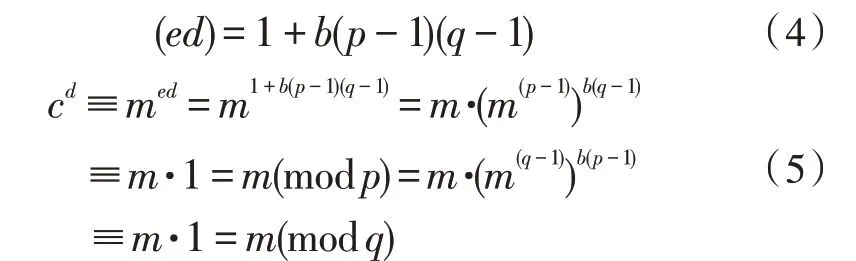
若mp-1≡1(modp) 且mq-1≡1(modq)，则(p,q)=1，故得cd≡m(modn)。

2）若(m,n)≠1，因m＜n，使p|m且q|m（或q|m且p|m），

因q|(med-m)，从p|m求得p|med-m，使其n|(med-m)。

因此，cd≡m(modn)。

同理可证如q|m且p|m仍有cd≡m(modn)。

2 RSA算法特性分析

知晓RSA 加密系统的学者，无不认为将大数合成进行因数分解[15]才是唯一破解的途径，却不知该系统所存在的缺陷，进行密码分析也是另一种破密方案。从数学发展的角度来看，因数分解具有NP 特性。如果因数分解技术有突破性进展，除直接对RSA 造成严重性威胁外，更可能导致该系统的整体瓦解。

符号表示如下：

m：message，亦即明文（Plaintext）

d：私钥（Private Key）

e：公钥（Public Key）

n：模数，即p与q的乘积

c：密文（Cipher），加密后的结果

令m=3 803，e=29，d=2 869，n=5 353(p×q=101×53)，则c=2 955。

加密阶段：

解密阶段：

由表1 可知，明文经由公开密钥加密后，即为密文。公开密钥和密文是网络上公开易得知的参数，由密文逆向推导为明文，很难直接计算求得私钥。然而将密文重复加密数次之后，又回到原点，此一特性突显解密私钥是冗余的，另一方面，显示加密至解密之间的过程具有线性特征。由表2 可见解密至加密的过程，实际上是加密的逆序，因此，该系统确实存在明文密文之间的递归关系。

由方程式（7）和（8），以及表1 和表2 不难观察到，明文3 803 只要连序加密30 次，便能返回原本的值；反之，密文2 955 也是连续解密30 次便还原成为初始的数值，代表明文与密文之间存在一对一的映射关系，公钥e与私钥d虽然是配对关系，纵使没有密钥，密文连续加密k次后，也能还原成明文，所以不论是明文空间或是密文空间，这两者都是封闭的空间。封闭的空间即代表有限的元素，有限的周期，简言之，即多项式时间内的求解问题。

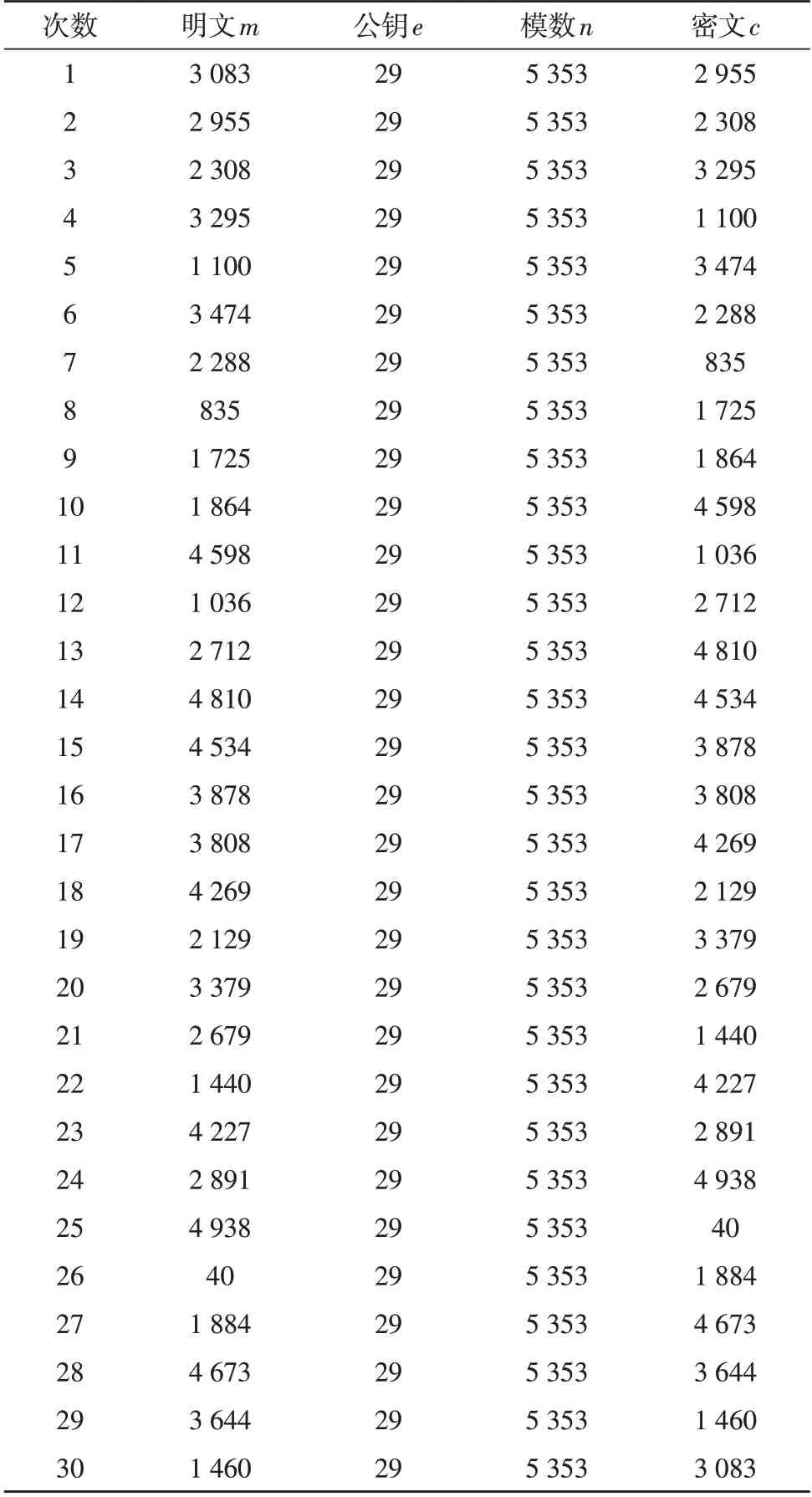
表1 加密阶段过程表

表2 解密阶段过程表

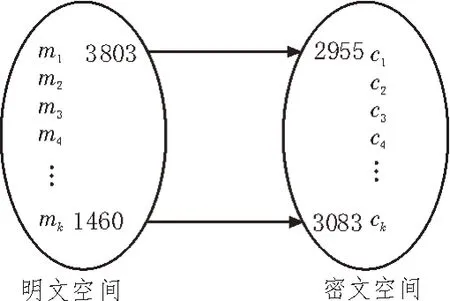
图1 明文密文映射关系图

Simmons 及Norris[16]首先证明RSA 算法p-1 和q-1 的最大公因数很小时，即不需要因数分解情況下容易被破解。该研究加密与解密阶段通过过程分析，直接观察明文和密文彼此变换的情形。

3 算法分析与破密方法

该文已探讨了明文和密文之间的联系是映射封闭空间的，现在将用逆推法，进行因数分解，以求得质数p和q的值。其步骤如下：

m：明文或未加密的信息。

n：模数为两质数p和q的乘积（p和q不公开）。

y：等同于φ(n)的值，目的在计算循环周期。

F：代表模数n除以y值后，取整数的值：

φ(r)∶φ(r)=(F·y)

步骤1：计算y值，并满足方程式（8）的条件，即：

因mφ(n)=m(p-1)(q-1)≡1(modn)，若my≡1(modn)，则有φ(n)|y的关系。

步骤2：计算F值，F=(ny)，模数n整除y后所获得的数据，也可表示为F=。

步骤3：计算φ(r)=(F·y)，φ(r)为两数及y的乘积。

步骤4：比较φ(r)=φ(n)，若φ(r)=φ(n)，则进行φ(r)之因数分解，若φ(r)≠φ(n)，则调整F值（上下加减一以计算φ(r)）。

例：假设m=184 且n=50 621，计算y,184y=1(mod 50 621)，得y=678。

计算F，F=(50 621/678)=74。

求φ(r)，φ(r)=74×678=50 172。

比较φ(r) 是否等于φ(n)，通过方程式（1）及（2）得知，mφ(n)≡1(modn)。

再验证方程式（10）φ(r)的计算结果，18450172mod 50 621=1。

已知φ(r)为50 172，分解其因数φ(r)得结果，即50 172=22×3×37×113。

再由方程式φ(n)=(p-1)(q-1)推论，便能获得p=(2×113+1)=227 和q=(2×3×37)+1=223，此处容易验证227×223=50 621 便是RSA 模数n。

方程式（9）以费马小定理为基础，目的着重于解离散对数的问题，将方程式φ(r)=(F·y)所计算的值进行分解，即为因数分解。该节取样148 932 个数据，质数选定（2＜p，q＜1 999 979）区间，正确数为148 907 个，错误数为25 个，正确率为99.983 1%。实验数据见表3。

表3 实验数据表

4 结论

该文通过将密文重复加密数次之后，显示明文与密文之间的映射关系，即解密实际上是加密的逆序。经过实验论证，该系统确实存在明文密文之间的递归关系，又通过逆推法，进行因数分解，正确率达99.983 1%，指出当前RSA 密码系统所存在的安全隐患。

研究初步采用软件计算的模式，用时间换取成本，在有效时间内达到解离散对数与因数分解的双重效果。另一方面，虽然采用简易的个人电脑实现了高位数的计算能力，然而当前样本数量仍然不足，希望增加样本数量，获得更加准确的数值。下一步将以数论作为基础，来完成相应的演算论证。