基于数据驱动的货车地铁协同配送路径优化

彭 勇，赵子翔，肖云鹏

（1.重庆交通大学交通运输学院，重庆 400074；2.重庆市市政设计研究院，重庆 400020）

文献[1]完成了短途客运与货运的结合，并提出了一种自适应大邻域搜索算法对其进行求解。文献[2-4]提出利用地铁网络进行城市货运并进行枢纽站点选址。文献[5]构建了地铁配送网络优化模型，并设计了一种随机变邻域迭代局部搜索算法进行求解。文献[6]将地铁与地面交通相结合建立了POM 模型，并用遗传算法进行求解。文献[7]建立了地下物流优化模型，并用遗传算法进行求解。文献[8]构建了多目标优化模型，并用蚁群算法进行求解。文献[9]构建货车地铁联运的配送路径优化模型，并通过改进自适应遗传算法进行求解。文献[10]提出深度学习辅助启发式树搜索方法，实现加速求解问题。文献[11]使用机器学习提高解的质量，并降低计算时间。文献[12]通过机器学习加速优化模型求解并进行验证。文献[13]通过使用机器学习生成目标函数计算替代方法求解大规模问题。文献[14]和文献[15]使用蒙特卡罗仿真解决问题中的不确定性问题。文献[16]引入数据驱动策略解决了蒙特卡罗仿真的高耗时问题。

综上，该文基于货车地铁协同配送网络，考虑货车配送过程中时间的不确定性、货车容量、地铁班期及转运花费等影响因素，建立不确定环境下以总配送成本和总配送时间为目标的多目标优化模型。并设计了以蚁群算法为主体，结合蒙特卡罗仿真和Pareto理论的多目标仿真蚁群算法，在此基础上引入结合数据池和机器学习算法的数据驱动策略加速问题的求解，构建基于数据驱动的多目标仿真蚁群算法。

1 问题描述与模型建立

1.1 问题描述

在城市物流配送中，选择地铁客流平峰期进行货车地铁协同配送。当有货物运输需求时，货车在寄件人处收集货物运输至地铁转运站点，由地铁转运到预定的卸货转运站点处，再由货车进行运输配送。在整个过程中，地铁线路具有固定班期，货物在转运站点通过地铁运输可能会产生等待时间。而在货物转运过程中也会产生一定的时间和成本。货车地铁协同配送模式图如图1 所示。

图1 货车地铁协同配送模式图

1.2 假设条件

假设1：货物寄件人和收件人的需求都是已知的，客户随机分配给地铁转运站点；

假设2：货车都相同，没有里程限制，且完成配送后不用回到起点；

假设3：地铁按固定班期发车，均有足够容量能装载货物，且货物能转运时立刻开始转运；

假设4：不同节点间运输时间随机分布。

1.3 参数与决策变量说明

参数定义：货车地铁协同配送网络为G=(N,E)，其中，N表示节点集(NC为客户节点，p为货车停车点，p∈N，NS为地铁站点，NT为转运点集合，NC⊂N，NT⊂NS⊂N)，边集为E={Eij|i,j∈N} 。当i∈NC时，i为货物寄件人节点，i＇为与之对应的货物收件人节点，满足i＇∈NC，(i,i＇)表示货物寄件人与收件人的组合。V为完成货物收集的货车集合（货车v∈V），V＇为将货物交付至收件人的货车集合（货车v＇∈V＇），R为地铁列车合集（列车r∈R）。其他符号表示如下，其中上标“～”表示不确定变量：

C：总配送成本；

：总配送时间；

cv：货车v的固定成本；

xv：货物运输过程中使用过货车v时为1；

Q：货车最大容量；

ϖk：在节点k处地铁的发班周期。

决策变量表示如下：

xv：货车参与配送时取值为1，否则为0；

：货车参与配送时取值为1，否则为0。

1.4 模型建立

该文建立的不确定环境下货车地铁协同配送路径多目标优化模型的目标函数为minZ=[C,]，其中，运输成本C如式（1）所示，总时间如式（2）所示：

式（3）表示货车的容量限制：

式（4）-（7）为流量约束：

式（8）-（10）为时间约束:

2 算法设计

该文研究的问题属于NP-hard 问题，采用启发式算法（蚁群算法）进行求解。文中构建了DDS-MSAC算法，分为MSAC 与数据驱动两部分，MSAC 为主体，负责配送方案并寻找评估，并得到求解结果。数据驱动具有加速MSAC 求解的功能，通过数据池收集数据和机器学习建模辅助MSAC 流程中目标值的计算，降低目标值计算消耗时间，流程图如图2所示。

图2 DDS-MSAC算法流程图

DDS-MSAC 算法步骤如下：

1）算法初始化。

2）蚂蚁移动配送路径。

3）路径对比和目标值计算。标记该次迭代中未被数据池收录的配送方案，计算该方案的配送成本；若替代方法误差满足要求，使用替代方法进行总配送时间预测，否则用蒙特卡罗仿真计算。

4）数据池归档。完成目标值计算后，将其录入数据池完成更新。

5）目标函数计算替代方法构建及其误差计算。若替代方法不满足误差要求，利用机器学习构建替代方法并重新统计模型预测误差；否则，跳过该步骤。

6）非支配排序。利用快速非支配排序算法寻找可行解集中的Pareto 解。

7）信息素更新。

8）替代方法参数修正。如果采用替代方法计算的方案比例大于数据池的阈值要求，则使用蒙特卡罗仿真重新计算，更新数据池后，对替代方法进行训练并统计模型预测误差；否则，跳过该步骤。

3 结果分析

3.1 算法分析

常用于构造目标函数计算替代方法的机器学习算法有GPR、SVR、RF 和BP 神经网络等。分析对比不同机器学习算法在该文研究问题上的优劣，选取性能较好的机器学习算法构建数据驱动中的替代方法加速策略。分别设置20、30 和50 节点规模的抽象算例，运行MSAC 进行求解，选取平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、均方根误差（RMSE）和时间作为评价指标。

由表1 可知，RF 在该文研究问题情况下表现最优，选择RF 作为构造目标函数计算替代方法的数据驱动方法。对数据驱动加速策略进行对比分析。分别构造基于数据池的多目标仿真蚁群算法（DPSMSAC）、基于RF 实现替代方法的多目标仿真蚁群算法（RF-MSAC）、基于数据驱动的多目标仿真蚁群算法（DDS-MSAC）。设置MSAC 算法实现平台不变，数据池阈值取30%，MAPE 小于5%时，RF-MSAC 和DDS-MSAC 使用替代函数。

表1 不同节点规模下机器学习评价指标结果

如图3 所示，在不同问题规模下，DDS-MSAC 算法加速求解效果明显，加速效率接近50%，且随着问题规模增加时加速效率较为稳定。因此，DDSMSAC 能够有效求解该文研究的问题。

图3 不同加速策略下问题求解用时

3.2 案例分析

3.2.1 案例描述

该文以重庆市轨道交通三号线及其周边快递站点构建货车地铁协同配送实例。

如图4 所示，设置配送实例网络。货物需从南岸区运送至渝中区或北部片区。设置货车容量为80，车辆固定成本为100 元，地铁单位货物运输成本为0.2 元/km，货车单位货物运输成本为0.6 元/km，转运成本为30 元/次，转运时间为5 min/次，满足运输条件的地铁发班间隔为30 min，各点间配送需求满足[20,40]均布分布。

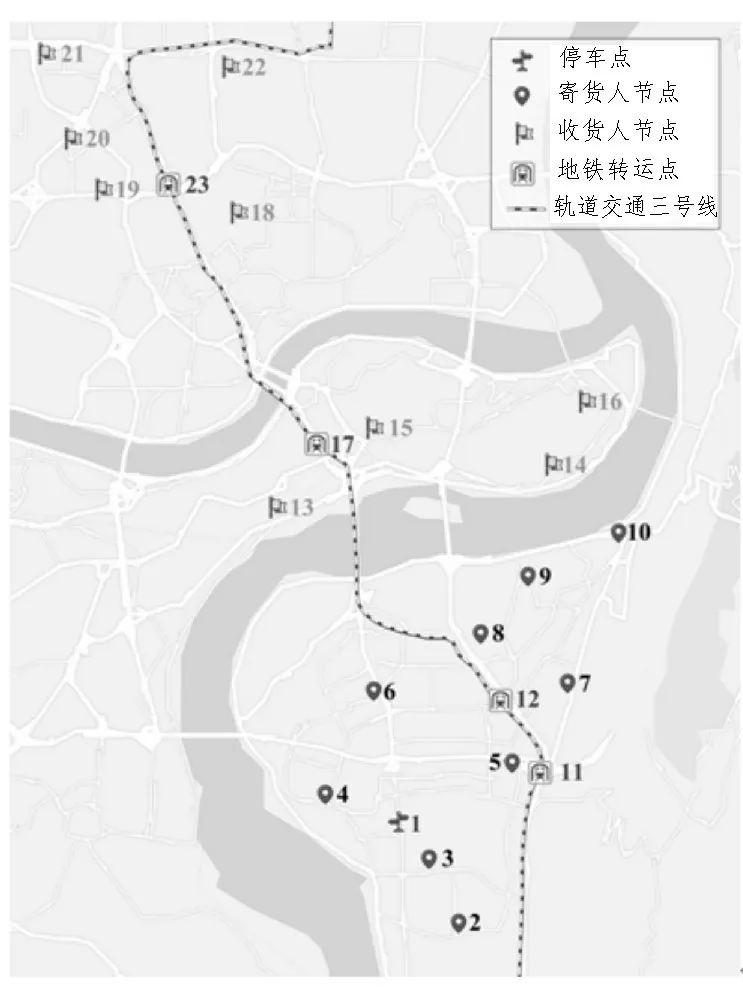
图4 实例配送网络图

3.2.2 求解结果分析

对DDS-MSAC 算法参数进行设置：蚂蚁数量取30；迭代次数取30 次；蒙特卡罗抽样次数取1 000次；信息素启发因子α=0.6 ；能见度启发因子β=0.3；信息素挥发因子ρ=0.3；替代函数的使用依据为MAPE 小于5%，数据池阈值取30%。利用Matlab（R2016a）软件编程进行求解，部分Pareto 解如表2 所示。

由表2 中的配送方案结果可知，货物由南岸片区运输至北部片区采用的是货车地铁协同配送；而货物由南岸片区运输至渝中片区都采用货车单独配送。如果决策者对配送方案的成本更为敏感，选择方案1；如果决策者更多考虑货物运输带来的负面影响，则选择方案2。

表2 货车地铁协同配送模式部分Pareto解

对比分析货车地铁协同配送和货车单独配送两种模式，删除实例中的地铁转运点，构建货车单独配送路径优化网络，采用DDS-MSAC 进行求解，求解结果如表3 所示。

表3 货车单独配送模式部分Pareto解

由表3 可知，货车地铁协同配送模式比货车单独配送模式有明显的优势。在货物配送过程中采用了运输价格较低的地铁，使得总配送成本下降。同时因为地铁运输速度快、延误少，减少了总配送时间。在货车地铁协同配送模式中，长距离运输由地铁完成，货车负责货物的收集和转运后的交付，货车的行驶距离更短，排放少，对环境更友好。

3.2.3 参数敏感性分析

对货车容量和地铁发班间隔两个参数分别进行讨论。实例和算法参数设置保持不变，改变货车容量下实例求解结果如表4 所示。

表4 不同货车容量下求解结果

由表4 结果可知，随着货车容量增加，货车最大行驶距离增加，货车数量和总配送成本降低，而配送时间在货车容量为120 时最小，最小载货率在货车容量为100 时取得。因此，在决策过程中，除了考虑成本和时间外，还需要考虑货车容量和货车载货率，减少运力浪费。

改变地铁发班间隔，求解结果如表5 所示。

表5 不同发班间隔下求解结果

表5 中，随着发班间隔的增加，地铁配送货物数量增加，总配送时间增加；但由于货物配送决策的发生变化，总配送成本不一定增加。因此，在决策过程中，当地铁运力余量较大时，可以通过调整发班间隔将货物集中进行配送，降低货物运输对地铁客运的影响。

4 结束语

该文综合考虑货车运输时间的不确定性和地铁班期限制，建立了货车地铁协同配送的路径多目标优化模型。通过基于数据驱动的多目标蚁群算法，对问题进行有效求解，为货车地铁协同配送提供实践参考，实现总配送时间和成本最少。该文设计了一种新的DDS-MSAC 算法，并分析验证了算法的有效性。以重庆市轨道交通三号线和其周边部分快递网点为实例，检验模型的实践可行性，同时验证了Pareto 理论在解决该问题上的优势。通过实例对货车地铁协同配送模式和单一货车配送模式进行比较，得出货车地铁协同配送模式在总配送时间、成本等方面都有明显优化，同时发现货车容量和发车间隔都会对配送结果产生影响。