基于数据摘要的流式子模优化算法研究
2023-02-23王耀力郝慧琴
王 怡,常 青,王耀力,郝慧琴
(1.太原理工大学信息与计算机学院,山西 晋中 030600;2.中国电信股份有限公司山西分公司,山西太原 030000)
当前,数据摘要逐渐成为机器学习的研究热点。然而数据摘要算法被证明在性别、种族和民族等敏感属性方面存在偏见[1-2],尤其在教育、招聘、银行和司法系统等领域中[3-5],所引起的公平性问题[6]得到了广泛的关注。
对于上述问题,该文引入流式子模最大化算法[7],在此基础上改进算法约束,考虑数据项的组成性,在每组中选取指定范围内的元素构成具有代表性的子集,从而使提取出的子集更具有公平性和多样性。
1 基于公平约束的流式子模算法
1.1 拟阵约束下的流式子模最大化模型
在很多情况下,考虑算法的稳定性以及成本等问题,通常采用拟阵约束下的流式子模优化模型[8-10]。
定义1:假设V表示原有数据集中n个元素的集合,V1…Vm是V的一个分划,即是m个非负整数,k为基数约束,S为最优子集。记:

则(V,L)是定义在V上的拟阵,称为分划拟阵。在分划拟阵约束下的流式子模最大化模型可表示为:

1.2 改进后的约束——公平约束
鉴于上述拟阵约束得到的集合S,当原始数据集合V中含有某些如年龄、性别、种族等特定属性时,会造成对某些特定属性数据的代表性不足或者过强,无法保证集合S的公平性与多样性。为了使选取出的集合S能够公平代表原始数据集合V,对上述拟阵约束进行改进,提出了一种公平约束。
该文借鉴文献[11-14]有关公平的思想,要求获得的解集S与数据某些特定属性(如种族、性别)相平衡,提出流式子模最大化下的公平约束,定义如下:
假定给定的数据集V是有颜色的,即给每个元素赋予一种颜色。对于颜色c=1,2,…,C,用Vc表示颜色c的元素集合,则b=1,2,…,C。对于每种颜色c,提取后的解集S必须包含每个颜色c的元素个数在指定的下界lc和上界uc之间。设k∊Z是一个全局基数约束,该公平约束表示为:

则基于该公平约束下的流式子模最大化模型为:

由公平约束的定义可知,S满足以下条件:

该文将满足上述条件的S表示为“可扩展”的。
2 公平约束下的流式子模算法
2.1 公平约束下的流式子模最大化算法
文献[8]提出的拟阵约束子模优化算法A(MSM算法)是目前性能最好的拟阵子模优化算法,但该算法未考虑公平问题。因此该文基于MSM 算法进行改进,提出公平约束下的流式子模算法(FSM 算法),步骤如下:
1)FSM 算法通过运行A来构造一个近似最大化f的解集SA。SA必定满足上界,同时,对于每种颜色c,并行收集一个大小为|Bc|=lc的备份集Bc。
2)若SA不满足其下界,则将SA扩展为一个可行的解决方案S,即对于每一种颜色c,如果|SA∩Vc|<lc,则从Bc中添加lc-|SA∩Vc|个元素来满足下界。
FSM 算法伪代码如下:

2.2 算法可行性分析
当去掉公平约束F中的下界约束|S∩Vc|≥lc时,剩下的约束将会与式(1)相同,得到一个拟阵。然而在该拟阵约束下的流式子模最大化算法A得到的解可能会违反下界约束。为了兼顾下界约束,该文算法通过从A并行流中收集备份元素来扩大解决方案,使之成为一个可行的解决方案。
然而,仅仅扩大解决方案来满足下界约束,可能会违反全局基数约束|S|≤k。正确的约束是解决方案具有式(5)的条件:“可扩展”到一个可行集。为了说明该文所提出的算法能有效地找到可行解,需要证明符合公平约束的V的可扩展子集的集合F仍然能构成一个拟阵。下面给出公平约束符合拟阵约束性质的证明。
定义2:若~2V是V的所有可扩展子集的集族,那么是一个拟阵。
证明如下:若是拟阵,必然满足以下公理:设B包含拟阵中的所有极大集。则B满足以下两个公理:
①B。
②如果B1,B2∈B和x∈B1B2,则存在y∈B2B1,使得B1-x+y∈B(向下封闭性)。
这些公理表明向下封闭性的B(集合的所有子集)是一个拟阵。但是,B的向下封闭性等于,因为V的任何子集只要能推广到一个可行解,也能推广到一个极大可行解。因此,只需要证明公理①和公理②。
公理①的证明只需假设≠∅,即可得到B≠∅。
对于公理②:已知B1,B2∈B,x∈B1B2,设c是x的颜色,一种简单的情况是当B2B1包含某个元素y∈Vc,那么B1-x+y中每种颜色的元素数与B1相同,因此B1-x+y也在B中。
现在假设另一种情况,即Vc∩B2⊆B1-x。那么有:

3 仿真实验与分析
3.1 实验概述
该文讨论的是公平约束下的数据摘要问题,为此通过以下指标来进行对比实验:
1)使用函数效用值和时间复杂度(运行时间)来衡量算法的性能。
2)将违反公平的次数error(S)=定义为衡量公平的标准,总和项的每一项是依靠违反上界和下界元素的个数来量化的。
3)查看不同算法每个分组的选取元素的个数来衡量提取数据的多样性。
实验所采用的效用函数为f(S)=M-d(v,e) 。其中,为数据集中的所有数据之和,其个数为n。
此外,平均每个分组提取到的元素为k/t,其中t表示分组的个数,根据该实验数据集的分组个数,设置上界uc=0.2k与下界lc=0.1k,以确保每个分组包含子集的10%~20%。
在很多应用中,比如电影推荐[15-16]、图形检测[17]等,感兴趣的是从庞大的数据集中提取出的部分集合与原始数据集相似,涵盖想要的所有的属性。
为了评估该文算法FSM 的可使用性,选用了两种不同的数据集,第一种数据集为公共数据集Cencus1990,其中含有一些可能导致算法偏见的属性(如年龄、身高、体重、性别、种族等),该实验选用该数据中的50 060 条记录,希望从该数据集中提取到能够涵盖原始数据集的所有年龄段的子集。该实验根据年龄将数据分为六组:[0,29]、[30,39]、[40,49]、[50,59]、[60,69]、[70+],各个年龄段的记录数分别如下:1 379、18 093、15 354、8 210、6 521、503。
第二种数据集是从吕梁山山脉观测得到的森林覆盖类型数据,该数据集共包含8 种可燃物林木类型:华北落叶松(1)、云杉(2)、白桦(3)、山杨(4)、辽东栎(5)、青木千(6)、侧柏(7)、醋柳(8),包含每种可燃物类型对应的海拔高度、土壤类型、坡度、坡向等12 种属性。每种可燃物类型分别有87 145、60 450、58 762、45 040、42 098、20 625、534、456 条数据。由统计数据可得侧柏(7)与醋柳(8)两种可燃物类型的数据量较少,传统算法在训练时容易忽略小样本数据。
将该文的FSM 算法与随机提取算法和MSM 算法进行比较。
3.2 不同算法下损失成本及运行时间对比
该文针对流式子模最大化算法进行改进,为验证该算法的有效性,对比上述几种算法的函数效用值以及运行时间。
如图1 所示,该文FSM 算法的函数效用值略低于MSM 算法,但优于随机提取算法。这是由于复杂约束的引入会不可避免导致算法效用降低。从实验来看,FSM 算法与MSM 算法相比效用值近似,甚至在提取的个数越大时,FSM 效用值与MSM 算法一致。

图1 不同算法下的函数效用值
流式子模最大化算法的运行时间是通过子模函数调用的次数来衡量的[7],与随机提取算法运行时间定义不一致,因此随机提取算法未涉及运行时间的对比。
如图2 所示,该文提出的FSM 算法的运行时间明显低于其他算法。且随着k的增大,FSM 算法对比MSM 算法运行效率有显著提升。在“森林”数据集下,当k为70 时,FSM 的算法比MSM 算法运行时间降低了8.6%。说明FSM 算法能大大减少时间复杂度,尤其在应用大型数据摘要问题中,FSM 算法更具有优越性。

图2 不同算法下的运行时间
3.3 不同算法下违反公平的次数对比
该文通过设置上界uc和下界lc来保证算法提取出的子集包含想要的数据属性值的所有范围,以此显示该文算法的公平性。因此将违反上界和下界元素的个数定义为违反公平的次数error 。通过对比不同算法违反公平的次数error 来验证该文算法的公平性。
由图3 可知,随着提取元素个数k的不断增大,MSM 算法与随机提取算法会出现不同程度的error。如当k设定为70,Cencus1990 数据集下随机提取算法的error 为28,MSM 算法的error 为21。而该文FSM 算法违反公平的次数始终为0,可有效保证提取的子集不会违反上界和下界,证明了该文算法的公平性。

图3 不同算法下的违反公平的次数情况
3.4 不同算法下的各个分组元素提取情况
该文所提算法的目的在于能够提取各个分组的元素,以使提取出的代表性子集具有多样性。通过分析查看不同算法下各个分组元素提取情况来证明算法的有效性。
分别选取k=30、k=70 不同情况来查看不同算法下的各个分组元素提取情况,如表1-4 所示。
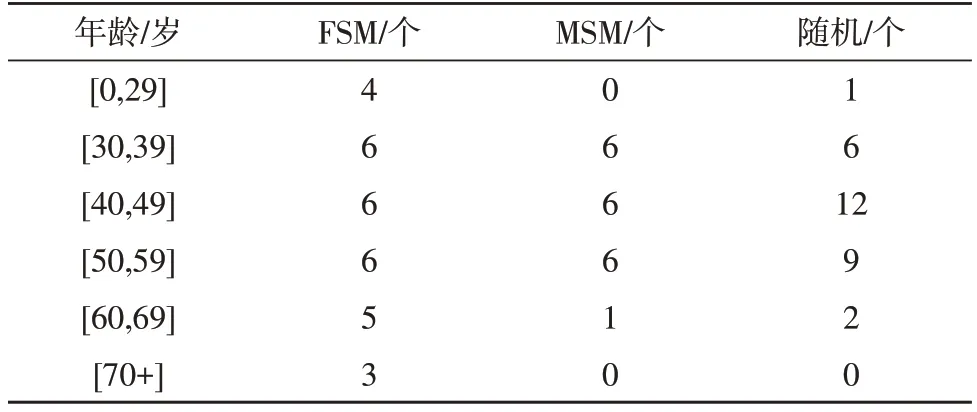
表1 Cencus1990 k=30 时不同算法下不同年龄段元素提取情况

表2 Cencus1990 k=70 时不同算法下不同年龄段元素提取情况

表3 “森林”k=30 时不同算法下不同林型元素提取情况
该文所提FSM 算法的核心在于对每个属性分组数据的提取添加了上界uc与下界lc约束。如表1-表4 所示,当提取数据k为30 时,上界值为0.2k=6,下界值为0.1k=3。因此属性每个分组被提取出的数据个数应当在3-6 之间。对比在Cencus1990 公共数据集和“森林”数据集下,随机提取算法与MSM 算法无法保证提取到所有分组类型的数据。在“森林”数据集中,当提取元素个数k=70 时,随机提取算法未提取到林型(8)的数据,MSM 算法未能提取到林型(7)和林型(8)的数据。可以看出,不论k取何值,FSM 算法提取的子集更具有代表性与多样性,证明了该文算法有良好的鲁棒性。

表4 “森林”k=70 时不同算法下不同林型元素提取情况
4 结论
该文讨论了数据摘要的代表性问题,提出了一种公平约束下的流式子模最大化算法,使选出的代表性子集能够涵盖提取属性的所有范围。实验表明,在该文模型下采用流式子模优化算法,相比其他流式算法,时间复杂度减少8.6%以上,且提取出的摘要的多样性与稳定性更强,可以适用于更复杂的场景中。
