洗衣机波轮有限元分析及拓扑优化设计
2023-02-23贺雪梅李一帆杨昕雨
贺雪梅,李一帆,杨昕雨
(陕西科技大学设计与艺术学院,西安 710021)
波轮是波轮洗衣机中非常重要的塑料部件,其结构复杂,主要采用注塑成型。波轮洗衣机是依靠波轮高速运转所产生的涡流冲击衣物,利用摩擦和水流作用进行洗涤,从而达到去污效果[1-2]。波轮在洗涤衣物过程中受力情况复杂,洗衣机能否正常运行取决于波轮结构的强度、刚度与固有频率等力学性能。目前波轮结构的设计开发需制作样机并反复测试,效率较低且造成人力、物力大量消耗[3]。
王金荣等[4]采用Moldflow软件对洗衣机波轮盖模型进行最佳浇口位置分析和优化,并对保压曲线进行优化,提高产品精度。刘培坤等[5-6]使用Fluent软件对其双环道液体平衡环和传统液体平衡环的内部流场进行数值模拟,借助悬挂系统多体动力学测试平台,对平衡环的悬挂系统进行脱水过程的偏心位移测试;而陆思宇等[7]利用平衡环内液体流动产生的离心力来达到减振目的。陶金等[8]采用能量法对洗涤段振动信号进行自动分段及周期时域特征提取。
波轮结构优化及轻量化设计是洗衣机产品研究的关键点。运用有限元技术和拓扑优化方法对波轮结构进行分析与优化,能明确现有结构的问题和优化方向,对提高波轮结构的改进效率具有重大意义。笔者以某迷你洗衣机波轮为例,选择两种关键工况,通过有限元分析获得波轮最大形变区域、波轮应力集中区域、波轮运行中易产生最大形变趋势的区域。运用拓扑优化方法在保证波轮强度与刚度的同时进行轻量化设计。
1 波轮结构优化
1.1 现有波轮结构分析
首先对某迷你洗衣机已安装的波轮进行测绘获得波轮基本尺寸。图1为某迷你洗衣机已安装波轮。后续以测绘所得尺寸为参考确定波轮改进后尺寸。

图1 某迷你洗衣机波轮正反面
波轮搅动水流是个复杂的过程,难以量化,笔者以波轮每转一圈可直接接触并搅动的水量来反映该指标。其计算公式可等效简化为:
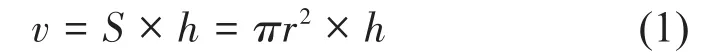
式中:v为体积,mm3;S为面积,mm2;h为高度,mm;r为半径,mm。
通过公式(1)可计算出波轮每转一圈可直接接触并搅动的水流体积为345 430.0 mm³。计算发现该波轮搅动的水流体积较小,即波轮直径过小,凸筋高度较低,故搅动水流效率较低。波轮凸筋与波轮接触处形状变化剧烈,易产生应力集中,导致局部应力过大。
查看洗衣机电机铭牌可知,洗衣机电机转速为1 320 r/min,实际测量可得电机轴与波轮轴之间的传动比为5∶1,计算得出洗衣机运行中波轮转速为264 r/min,转速较高,噪音较大。波轮结构存在的问题与解决方案见表1。

表1 波轮结构存在问题与解决方案
1.2 波轮结构改进
通过波轮每转一圈可直接接触并搅动的水流体积发现,原波轮直径较小。实际测量得到洗衣机桶内底部直径为340 mm,在波轮直径两侧为排水以及桶壁的扰流凸筋等结构各留50 mm,故波轮直径可增大为240 mm。基于波轮直径增加及尺寸变化,修订凸筋长、宽、高尺寸分别为85,16,10 mm。另,根据公式(1)可计算出波轮指标改进后的体积为723 530.0 mm³,即优化后波轮搅动水流的能力约为优化前的2.1倍,故优化后波轮转速可降为125.7 r/min。由此,可使用功率更小的电机,既可减少波轮因高速转动产生的噪音和振动,且洗涤作用力不会降低。波轮各指标改进后参数见表2。

表2 波轮原参数与改进后参数
2 有限元模型的建立
2.1 网格模型
首先,用Solid Works创建波轮三维模型,并将模型导出为Parasolid (*.x_t)格式,再将其导入ANSYS Workbench进行分析。
图2为ANSYS单元类型。如图2所示,因ANSYS单元库种类众多,同时波轮结构为实体模型且形状不规则,故选择SOLID186单元中的二阶四面体单元(退化的二阶六面体单元)进行有限元分析。选择二阶四面体单元为网格控制方法。因波轮主体厚度为2 mm,为保证波轮主体厚度至少有两层网格,故模型的整体网格尺寸设置为1 mm,以保证计算结果的准确性。对易产生应力集中区域,进行网格细化。为保证在应力最大区域覆盖到两层以上网格,局部网格尺寸设置为0.5 mm,以反映此处真实应力水平。网格单元总数为753 760,结点总数为1 260 048。点击Mesh Metric,选择单元质量数值来检查生成网格的质量,平均网格质量为0.81 485,表明网格划分结果良好。波轮网格模型如图3所示。
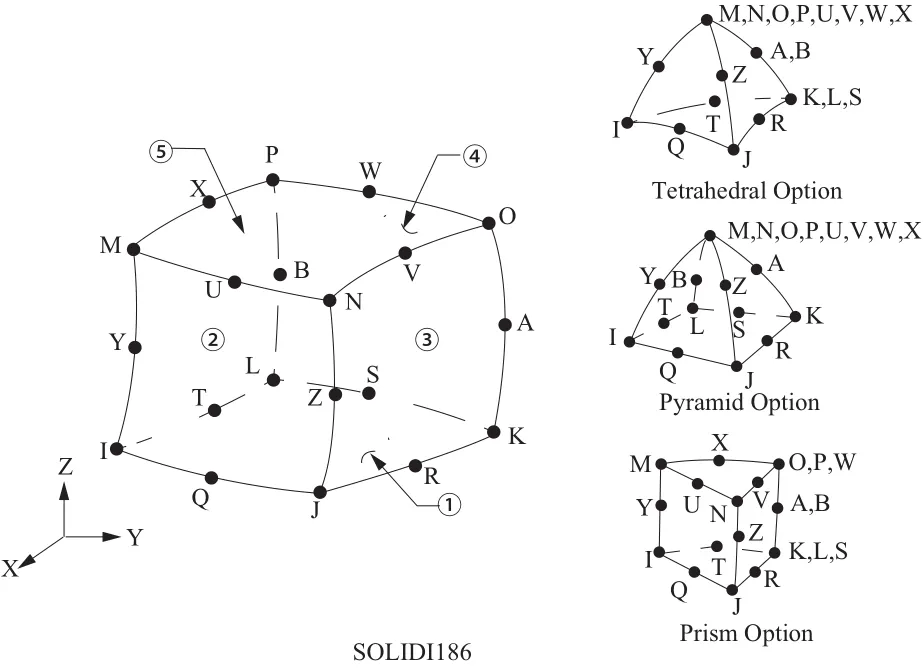
图2 ANSYS单元类型

图3 波轮有限元模型正反面
2.2 材料属性
选用耐磨聚丙烯为波轮材料。耐磨聚丙烯以高结晶均聚聚丙烯为原料,同时添加改性有机硅氧烷、相容剂和成核剂等助剂增强其润滑性能和硬度,以减少与衣服的摩擦,降低材料磨损[9-10]。改性后的耐磨聚丙烯力学性能见表3。

表3 耐磨聚丙烯力学性能
2.3 约束关系
洗衣机电机通过皮带传动装置驱动波轮轴转动,波轮仅在底部正方形孔处与波轮轴固连。因此约束类型为固定约束,约束面选择波轮底部中心孔处的五个面。
2.4 选取工况与确定载荷
洗衣机波轮在洗涤衣物过程中受力情况复杂,水的阻力、水流裹挟着衣物上下翻转产生的力等都作用在波轮结构上;又因洗衣机运行时波轮处于转动状态,会产生不同类型的组合形变,因此在有限元分析中,很难对波轮受到的所有作用力都进行分析,故需将波轮结构受到的冲击力及其它复合作用力简化为静力,即将动载荷简化成等效静载荷。
从波轮完成一次正反转的过程中提取两种关键工况进行分析,分别是波轮启动时工况与波轮正反转交替时工况。通过有限元仿真测试检验这两种工况下波轮的刚度与强度是否符合要求。
波轮启动时工况:波轮在水流完全静止的情况下启动并开始搅动水流的情况。
波轮启动时受到完全静止的水流阻力:即波轮启动时推动水流,水流对波轮凸筋产生的阻力,其计算公式为:

式中:m为单根波轮凸筋推动的水流质量;a为逆向水流的加速度。
由模拟简化计算可知,单根波轮凸筋推动的水流质量为0.18 kg,加速度为4.2 m/s2。计算可得波轮凸筋受到的力为F=0.76 N。
波轮正反转交替时工况:在水流方向与波轮即将转动方向相反条件下,启动反转并开始搅动水流的情况。
波轮正反转交替时,波轮转动方向与水流方向相反。波轮正反转交替时受到的力:即水流旋转产生的阻力与波轮启动受到水的阻力叠加。
由模拟简化计算可知,单根波轮凸筋推动的水流质量为0.18 kg,加速度为16.67 m/s2。由公式(2)可得波轮凸筋受到的力为F=3 N。
另外,在波轮反向旋转时,水流裹挟着衣物完成一定速度的转动。桶壁的扰流凸筋扰动水流使衣物上下翻转并对波轮表面产生作用力。通过实际洗涤过程中测力仪测量,这一作用力的峰值为8 N。后续静力学分析中,将这个作用力简化为8 N的静载荷,其方向垂直于波轮表面,作用面积为整个波轮表面。
3 波轮结构有限元分析
根据波轮有限元模型,对其进行静力学分析和模态分析,得出最大变形区域、应力集中区域以及各阶模态的振型,将其作为拓扑优化的基本条件,为后续研究提供依据。
3.1 波轮启动时工况静力学分析
将洗衣机波轮启动时的受力情况简化成4个施加在波轮凸筋上的静载荷进行静力学分析,即添加4个0.76 N的力在波轮凸筋的一侧,如图4所示。
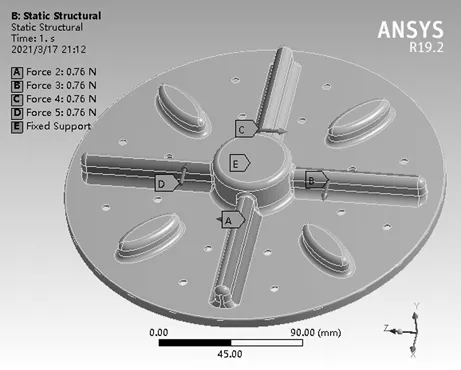
图4 添加载荷
图5为波轮总形变云图。由图5分析可知,波轮形变最大位置位于边缘,形变量为0.063 mm。因中心有固定约束,故距离波轮中心越近,形变量越小。耐磨聚丙烯材料本身可承受较大的弹性形变,0.063 mm的形变量在弹性变形的范围内且形变量很小,表明波轮结构具备良好的抗形变能力,同时说明波轮整体结构可能存在一定的厚度冗余。

图5 总形变云图正反面
图6为波轮应力云图。由图6分析可知,应力主要分布在波轮中心位置,应力最大值为0.33 MPa,应力最大处形状有剧烈变化,此处为应力奇异点,应力值无法测量。现实中不会出现这种形状剧烈变化的情况,故排除该最大值。排除应力奇异点后,应力最大值出现在凸筋与中心圆柱连接处,最大应力值为0.26 MPa。聚丙烯的许用应力[σ]范围在10 MPa至13.3 MPa之间。0.26 MPa远远小于10 MPa,故波轮强度符合要求。
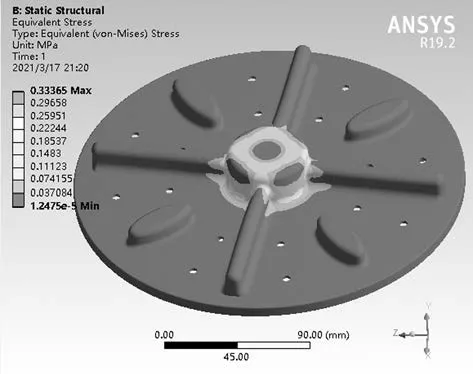
图6 应力云图
3.2 波轮正反转交替时工况静力学分析
如图7所示,将洗衣机波轮启动时的受力情况简化等效为4个施加在波轮凸筋上的力进行静力学分析,即添加4个3 N的力在波轮凸筋的一侧;波轮反向旋转时作用力为8 N,其方向垂直于波轮表面。
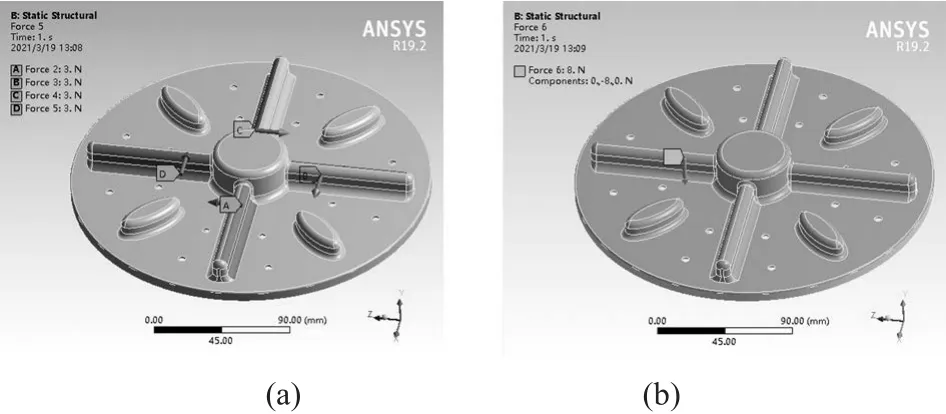
图7 波轮受力情况分析
图8为波轮总形变云图。由图8分析可知,波轮形变最大位置位于靠近沥水篮卡扣的边缘区域,最大总形变量为0.3 mm。

图8 总形变云图正反面
图9为波轮轴向形变图。由图9分析可知,轴向形变最大位置同样位于靠近沥水篮卡扣的边缘区域,形变量为0.18 mm。产生波轮轴向形变的原因是存在一个均布于波轮表面的载荷。
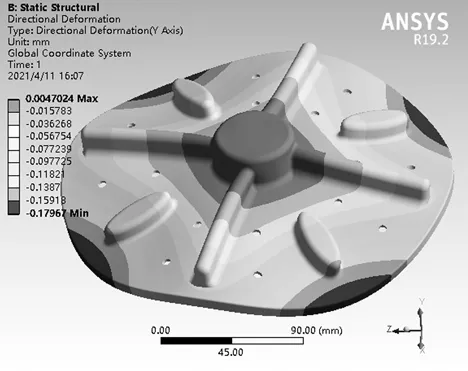
图9 波轮轴向形变图
虽然耐磨聚丙烯本身可承受较大弹性形变,但波轮结构长期变形后再复原,可能会导致疲劳损坏,因此,该区域可改进结构增强刚度。
从图10波轮应力云图可知,应力主要分布在波轮中心位置。排除应力奇异点后,应力最大值出现在凸筋与中心圆柱连接处,最大应力值为1.17 MPa。波轮强度符合要求。
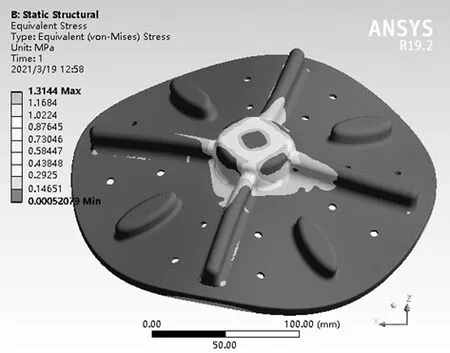
图10 应力云图
3.3 模态分析
波轮在洗涤衣物过程中受力情况复杂,水的阻力、衣物裹挟水流上下翻转产生的作用力等都作用在波轮结构上。波轮转动过程中还会受到来源于电机产生的振动激励,如果电机或传动系统不平衡等因素,造成振动频率在数值上接近、等于波轮结构的固有频率或激振频率的整数倍,可能会导致共振现象的产生,振幅增大并发出噪音,长期如此会造成波轮结构变形与疲劳损坏,影响洗衣机的安全性与使用寿命,故波轮结构要有良好的动力学性能。因此,确定迷你洗衣机波轮的固有频率及相应振型对迷你洗衣机波轮设计和改进有重要意义。
选择Ansys Workbench中Modal模块对波轮结构进行模态分析。因模态分析是线性的,故波轮在模态分析中不需要添加激励[10]。表4为通过模态分析求解得到的波轮结构前八阶模态。
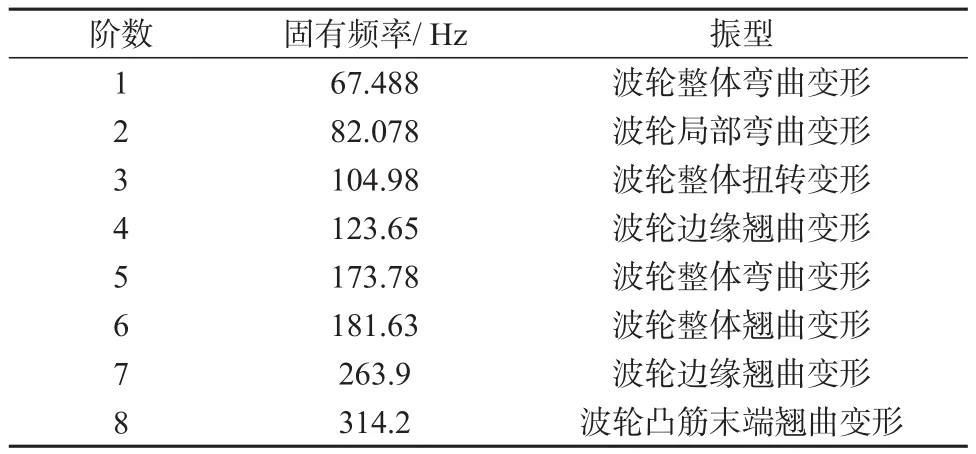
表4 波轮前8阶固有频率及问题描述
对各阶振型分析发现,随着模态阶数提高,波轮结构形变区域从刚度较小的波轮边缘区域发展到刚度较大的波轮凸筋末端区域。从单一变形发展为多样组合变形形式,从波轮边缘局部形变发展到波轮整体形变。故在实际情况中高阶模态下的形变很难发生,低阶模态的形变相对容易发生。
模态分析研究表明,洗衣机波轮的振动主要发生在边缘部分。洗衣机运行时主要的振动激励来自电机,迷你洗衣机采用的电机成本较低,转子大多存在质量不平衡情况,因此会产生相当于每秒钟转数的振动,洗衣机所采用的电机转速为1 320 r/min,计算得出洗衣机电机产生的振动频率为22 Hz,而各阶模态频率远大于22 Hz,且不为整数倍,故该洗衣机在洗涤衣物过程中共振现象不会发生,波轮动力学性能良好。另外,实际情况中可能存在其他频率的激励振动,在优化波轮结构同时,应提高波轮边缘位置强度和刚度,防止波轮结构损坏。
4 波轮拓扑优化
拓扑优化是一种在设计空间内优化材料分布与结构布局的数学方法,广泛应用于结构设计中[11-16]。另外,波轮正反转交替时工况受力更大且受力情况更复杂,故选择波轮正反转交替时工况进行拓扑优化分析。将波轮正反转交替时工况的静力学分析结果传递到拓扑优化分析模块,优化区域选择波轮整体,非优化区域选择约束区域和波轮工作表面。图11为13次迭代运算后的结果,Remove默认不显示,是程序建议清除位置,可以看出,去除区域大部分在波轮厚度上。keep是程序建议保留的位置。而Marginal为临界位置,既可保留也可去除。根据拓扑优化分析结果可知,对波轮结构进行优化时,需综合考虑各结构之间的关系。
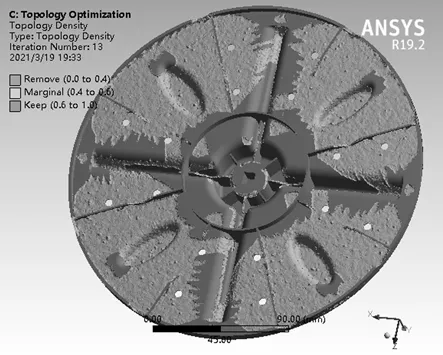
图11 波轮拓扑优化结果
对波轮进行以下优化:将波轮整体厚度减至1 mm,将凸筋与中心圆柱连接处厚度增加0.5 mm等。表5为波轮拓扑优化问题及解决方案。

表5 波轮拓扑优化后存在问题与解决方案
根据拓扑优化迭代计算结果,去除冗余材料;根据有限元分析,在形变量与运动中形变趋势最大区域局部增加加强筋结构。波轮拓扑优化改进后结构如图12所示。
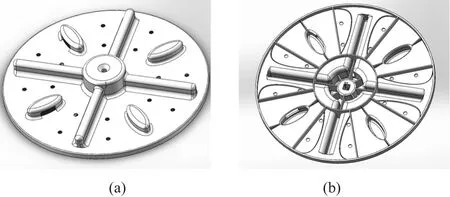
图12 改进后波轮结构
根据有限元分析与拓扑优化结果重新设计的波轮结构总质量为105 g,拓扑优化前质量为127.56 g,整体质量减少18%。
5 波轮刚度与强度验证
对优化后的波轮重新建立几何模型,因此需要重新划分网格,网格划分策略与前文相同。
如图13总形变云图可知,波轮发生形变最大位置位于靠近沥水篮卡扣的波轮边缘部分,最大形变量为0.28 mm。0.28 mm的形变量在弹性变形的范围内,优化前最大形变量为0.3 mm,表明优化改进后的波轮结构具备良好的抗形变能力。

图13 总形变云图
图14为波轮轴向形变。从图14可知,最大轴向形变量减少了33%,轴向刚度提升明显。波轮结构形变最大区域,刚度增加的同时质量减少18%,结构优化效果明显。
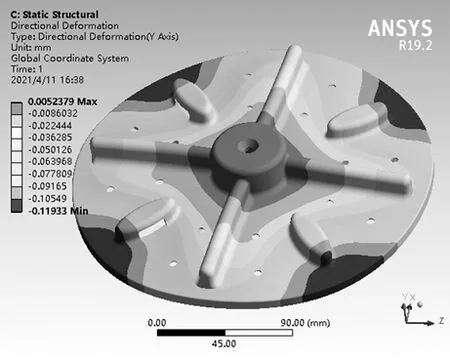
图14 波轮轴向形变
图15为应力云图。从图15可知,应力主要分布在波轮中心位置,排除应力奇异点后应力最大值出现在凸筋与中心圆柱连接处,最大应力值为1.03 MPa。优化前后的结果对比见表6。

图15 应力云图
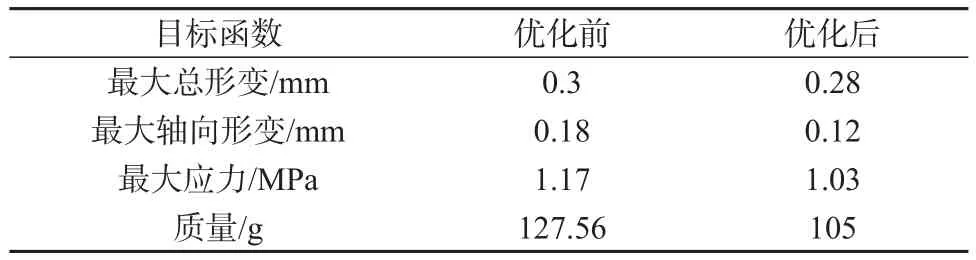
表6 优化前后结果对比
6 结论
将有限元分析与拓扑优化方法相结合,运用到迷你波轮洗衣机的波轮结构研究中。通过改进现有波轮结构参数,建立波轮结构的有限元模型,对其进行静力学分析和模态分析,研究波轮结构的形变与应力情况,提出优化建议,并通过拓扑优化计算,实现波轮结构的轻量化。优化后的结构,提升了波轮的洗涤效率与力学性能,并有效降低了波轮重量,减少材料消耗。此优化设计方法为波轮式洗衣机的结构设计提供一种新的思路,也为产品设计提供了一种新的方法和依据。
