基于GCTMSA的梯级水火风光蓄储联合调度

曹 韵，韩 松，荣 娜，詹献文，刘 敏

基于GCTMSA的梯级水火风光蓄储联合调度

曹 韵，韩 松，荣 娜，詹献文，刘 敏

(贵州大学电气工程学院，贵州 贵阳 550025)

为发展新型电力系统调度理论与方法，构建了一个含梯级水风光蓄一体出力(the integration of cascade hydro-wind-photovoltaic-pumped storage, CHWPPS)的水火风光蓄储联合调度模型。同时，针对传统求解方法在求解水火风光蓄储联合调度系统时易陷入局部最优、难以在满意时间内得出可行解等问题，提出了一种基于贪婪策略、自适应交叉算子和自适应t分布变异的改进飞蛾搜索算法(greedy strategy, adaptive crossover operator and adaptive t-distribution variation based moth search algorithm, GCTMSA)。GCTMSA将自适应交叉算子与Lévy飞行策略相结合，在直线飞行策略中引入自适应t分布变异，并利用贪婪策略仅接收更优个体，以提高全局搜索能力和搜索速度。算例分析在一个修改的IEEE 6机30节点系统和一个省域简化电力系统中展开。结果表明，与飞蛾搜索算法、遗传算法、粒子群算法和生物地理算法相比，GCTMSA具有更强的搜索能力和稳定性。同时，分析了CHWPPS和电池储能对系统的影响。相关讨论与结论可为水火风光蓄储联合调度等多能互补技术发展提供参考。

梯级水风光蓄一体化；自适应交叉算子；自适应t分布；贪婪策略；改进飞蛾搜索算法

0 引言

多能互补技术是我国构建以新能源为主体的新型电力系统的关键技术之一。它能充分利用不同能源的互补特性，整合可再生能源和可控能源，提升电网的灵活调度能力[1-3]。

目前，国内外学者已对不同类型的多能互补调度模型和方法等展开了大量研究。其一，从多能互补类型的角度来看，主要涉及了风-火[4]、水-光[5]、水-火-风-光[6-7]、风-光-火-储[8-9]等类型。其中，文献[4]将易控火电与风电进行联合调度，提升了风电在系统中的渗透率。文献[5]将清洁水电与光伏互补接入系统，一定程度上平滑了光伏出力波动。文献[6-7]以火电、水电和可控负荷为可调度资源，构建了一个日前调度系统，实现调度经济性与鲁棒性的平衡。文献[8-9]引入储能装置，利用其灵活吞吐能力应对风光出力的不确定性，提升能源利用效率。然而，梯级水风光蓄一体化(the integration of cascade hydro-wind-photovoltaic-pumped storage, CHWPPS)及其与火电耦合等的多能互补研究还未见报道。因此，开展水火风光蓄储联合调度研究对于发展新型电力系统调度理论与方法具有重要意义。

其二，从多能互补调度模型和求解方法角度来看，各能源间的强耦合性和可再生能源的随机性，使多能互补调度问题的可行域空间变得十分复杂[10-11]。拉格朗日松弛法[12]和梯度投影法[13]等传统求解方法效率低下，很难在满意时间内搜索到可行解。文献[14]构建了一个包含风光储在内的综合能源系统，在传统磷虾算法中引入线性递减策略，结合粒子群优化算法，有效提升模型求解效率。文献[15]建立了一种自适应增强的搜索性猎物机制来增强鲸群种群的多样性，防止算法陷入局部最优。文献[16]基于小波变异改进鲸鱼优化算法，与其他算法相比，改进的算法显著提高了系统经济性。文献[17]以最大源荷匹配度和最小弃电量为目标，构建了一个水光互补的源荷双层嵌套优化调度模型，采用改进的萤火虫算法进行求解，取得了显著的效果。从上述文献可以发现，采用元启发式算法求解多能互补系统优化调度问题是一条极具潜力的技术路线。近期提出的飞蛾搜索算法(moth search algorithm, MSA)[18]是一种新型元启发式算法，相关领域的应用研究表明其具有较好的求解效率等优点[19-21]。但暂未见MSA应用于新型电力系统调度领域的研究。

因此，为发展新型电力系统调度理论与方法，本文构建了一个含CHWPPS的水火风光蓄储联合经济调度模型。同时，为进一步提高MSA的搜索能力和稳定性，提出了一种基于贪婪策略、自适应交叉算子和自适应t分布变异的改进蛾群搜索算法(greedy strategy, adaptive crossover operator and adaptive t-distribution variation based moth search algorithm, GCTMSA)。一个修改的IEEE 6机30节点系统和一个省域简化电力系统的测试结果表明了本文所提模型和算法的有效性和优越性。

1 梯级水火风光蓄储低碳联合调度模型

1.1 目标函数

为考虑电力系统整体经济性，以综合成本最小为目标函数。

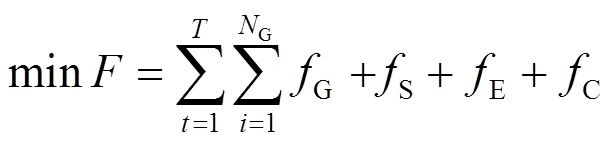
1) 火电机组运行成本

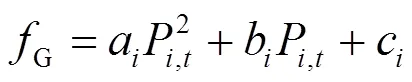
2) 电池储能机组运行成本

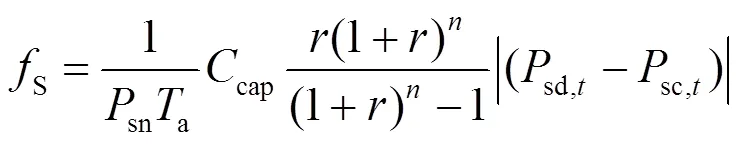
3) 碳交易成本

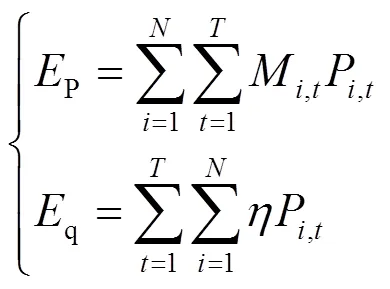
4) 弃风弃光成本

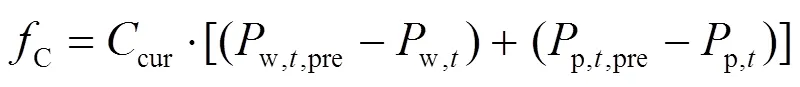
1.2 约束条件

1) 功率平衡约束

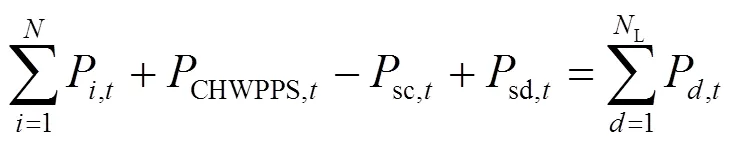
2) CHWPPS运行约束

不考虑能量交换过程，CHWPPS内部的电力流与水流情况如图1所示。

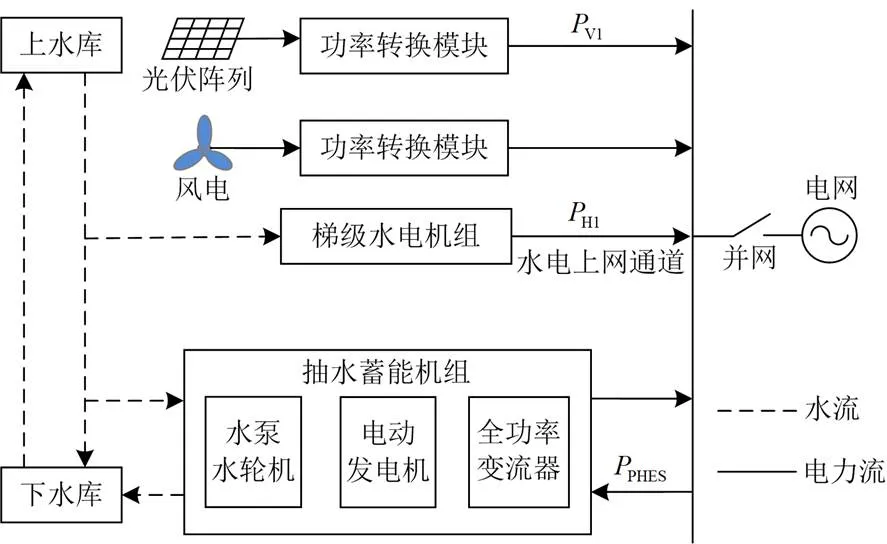
图1 梯级水风光蓄一体发电系统

CHWPPS出力约束为

式中，CHWPPS,N为梯级小水电机组总额定出力。

水电机组出力约束为

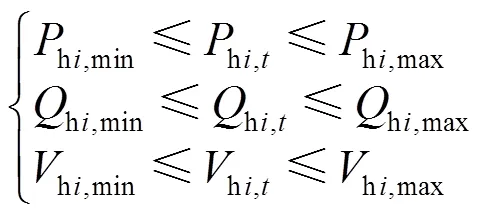
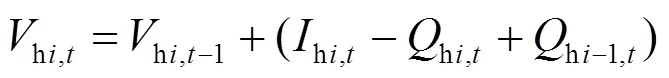
风电、光伏机组出力约束为

抽水蓄能机组约束为

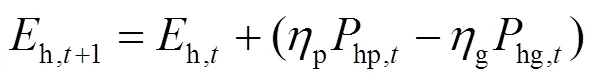
3) 火电机组运行约束

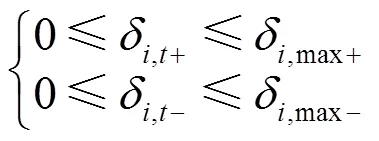
4) 电池储能机组运行约束

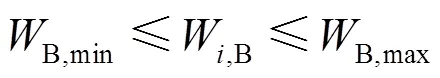
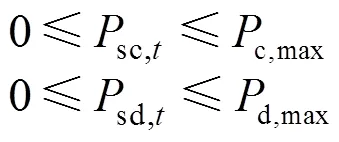
5) 网络安全约束

本文借助直流潮流表述潮流分布，引入功率转移分布因子(power transfer distribution factor, PTDF)直接描述节点有功功率与线路有功潮流的线性关系，使得电力调度优化模型无需考虑中间变量节点电压相角，基于PTDF的直流潮流计算方法能够获得与交流潮流相近的结果[22]。

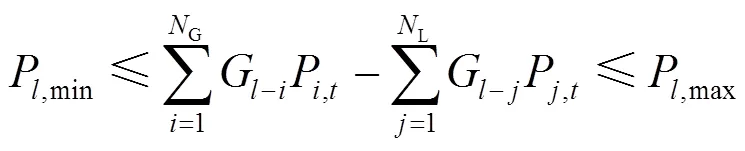
2 求解方法

2.1 飞蛾搜索算法

受飞蛾趋光性和Lévy飞行特性的启发，文献[18]提出了MSA。该算法按适应度值大小将整个种群分为两个相等的子群，适应度最好的飞蛾被视为光源，子群1中飞蛾利用Lévy飞行策略，依靠自身的位置信息扩大算法的搜索范围，如式(20)所示。

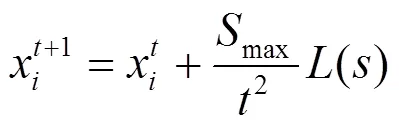
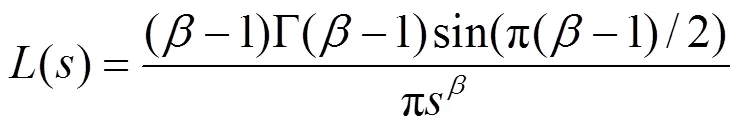
相反，子群2中适应度较低的飞蛾以直线飞行策略向光源迈进，更新公式如式(22)。

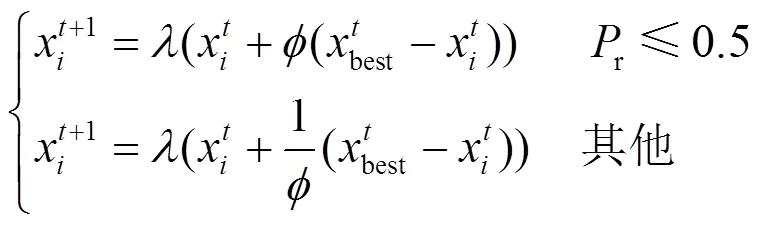
2.2 改进的飞蛾搜索算法

传统MSA中直线飞行算子的隐性学习机制主要集中于全局最优个体上，易陷入局部最优，收敛速度慢。要进一步改进MSA性能，需要深入研究维持种群多样性和共享优良信息的替代策略[21]。

1) 改进的自适应交叉算子

为充分共享飞蛾间信息，提升全局搜索能力及收敛速度，本文提出了一种自适应交叉算子，在MSA利用式(20)进行位置更新后，根据个体适应值对位置进行优化，使算法前期快速跳出局部最优，并提高迭代后期种群的多样性。具体公式如式(23)。

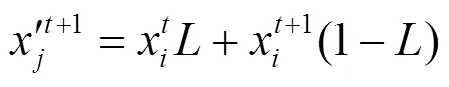
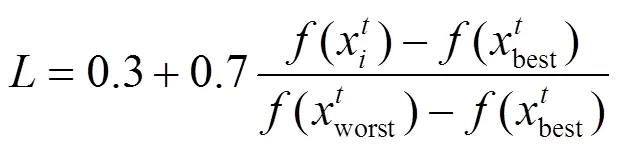
2) 自适应t分布变异

为进一步提升迭代后期种群多样性，提高算法全局搜索能力，本文在直线飞行策略中加入自适应t分布变异。

在智能优化算法中，常用柯西变异算子与高斯变异算子来提升算法的求解性能，柯西变异算子在全局搜索上有较强的能力，且在迭代过程中可以保持种群的多样性；而高斯变异算子在局部开发上有较强的搜索能力，能在一定程度上提高收敛速度。自适应t分布变异综合两者优点，将迭代次数视为自由度参数，其概率密度函数表达式如式(25)。

对飞蛾位置利用自适应t分布变异进行更新，如式(26)。

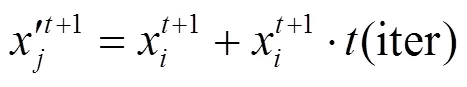
3) 贪婪策略

贪婪策略选择适应度更好的飞蛾个体更新。

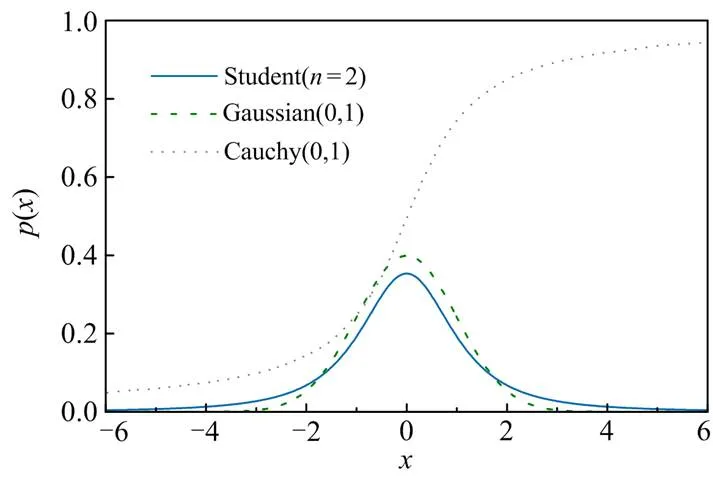
图2 柯西分布、t分布和高斯分布函数分布图

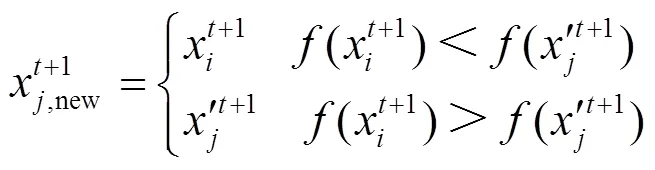
2.3 求解流程

综上，本文所提改进算法的流程如图3所示。

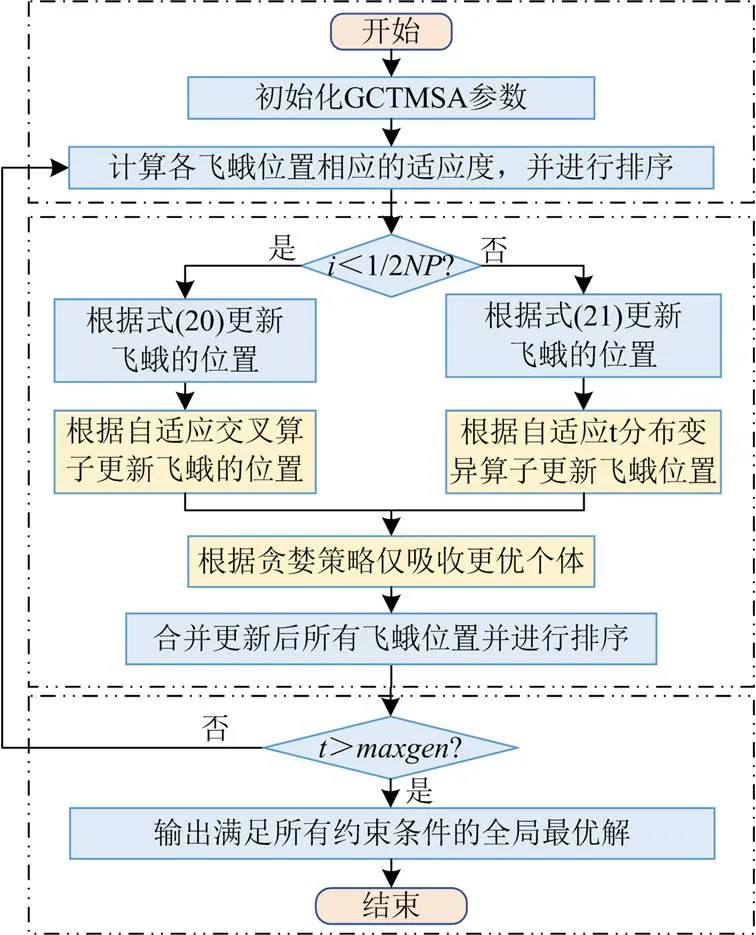
图3 GCTMSA流程图

Step2：计算飞蛾个体适应度值并排序。

Step3：将整个种群按照排序大小分为两个相等的子群。子群1通过Lévy飞行策略、自适应交叉算子更新飞蛾位置，子群2通过直线飞行算子、自适应t分布变异算子更新飞蛾位置，并通过贪婪策略更新更优飞蛾个体位置，合并新子群后进行排序。

Step4：判断是否大于迭代次数，若是，则输出最优可行解，否则返回Step3。

3 算例分析

3.1 IEEE 6机30节点系统仿真

为验证本文所提调度模型及方法的有效性及优越性，本文借助GCTMSA对一个修改的IEEE 6机30节点系统进行优化。系统接线图如图4所示，节点2接入一个电池储能机组，额定容量为233 MWh，其每小时最大充放电功率为±60 MW，充放电效率为0.9。节点3接入了一个CHWPPS，其中包含3个梯级小水电机组、1个风电机组、1个光伏机组及一个抽蓄机组，水风光规模比例根据雅砻江实际水风光一体电站1:0.34:0.4比例进行建模，抽蓄电站抽水与放电的功率为±30 MW，抽蓄电站参数[23]见表1，抽水和发电效率为0.9。火电机组参数见文献[24]，单位碳交易成本为40元/t，碳排放配额为0.8 t/MW。弃风弃光惩罚系数为200元/MWh，风电、光伏预测功率及典型日负荷如图5所示。GCTMSA的参数设置如下：每代保存飞蛾数量为2，最大移动步长为1，加速系数为0.618。所有算法的种群规模为100，迭代次数为3000，其他算法详细参数设置见文献[25]。

图4 一个修改的IEEE6机30节点系统

表1 抽水蓄能机组相关参数

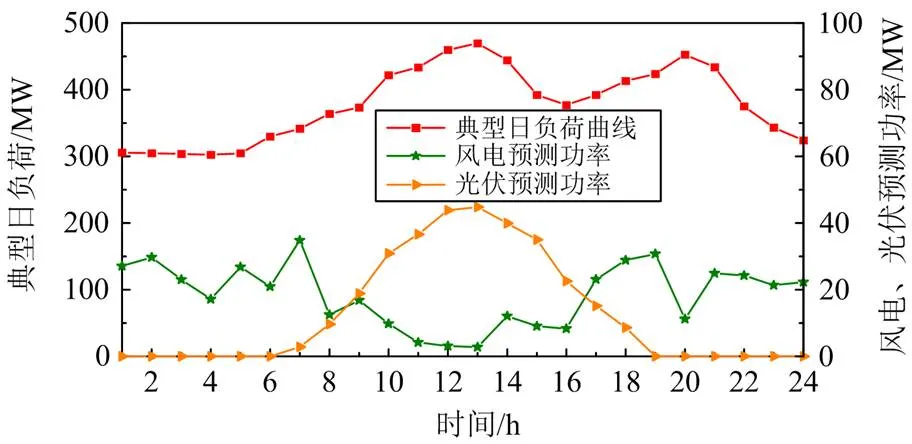
图5 风电、光伏预测功率及典型日负荷

1) 不同场景下的结果分析

为验证CHPPWS电站联合出力效益及抽蓄、电池储能机组对调度结果的影响，本文借助GCTMSA对3种场景进行求解，场景1：风、光、水、火参与调度，不考虑电池储能和抽蓄，考虑梯级水风光一体发电；场景2：风、光、水、火、抽蓄参与调度，不考虑电化学储能，考虑梯级水风光蓄一体发电；场景3：风、光、水、火、抽蓄、电化学储能参与调度，考虑梯级水风光蓄一体发电。各场景下优化调度结果如表2所示，图6为各场景下日前优化调度结果。

表2 各场景下结果参数比对I

综合观察表2与图6可知，3种场景下各能源出力总和均满足功率平衡约束。对比场景1、2可知，当梯级水、风、光、蓄一体接入电网时，抽蓄电站利用自身灵活吞吐的能力，在低峰负荷时，就地消纳了多余的水风光出力，在高峰负荷时输出储存电力，提升了CHWPPS总出力的同时减少了火电机组出力。此时，综合成本下降了13.39万元，碳排放量降低了128.61 t，弃风弃光量下降16.91%，通道利用率也由66.98%提升至71.42%。而随着场景3中电池储能机组的接入，系统的灵活调度能力得到了提升，储能在系统中占比达到了40%。电池储能机组为系统提供了大量的备用容量，并且可以快速安排自身调度空间贴合负荷需求，有效缓解了火电机组的调峰压力及其爬坡幅度，进一步减少火电机组出力，为CHWPPS出力创造空间，有效提高了系统低碳经济性。对比场景2、3，碳交易成本下降了0.36万元，弃风弃光量减少了99 MW，现有水电通道利用率由71.42%提升至74.41%。虽然电池储能的接入大大提升了电网的灵活性，但电池储能机组的使用将会造成一定的损耗成本，综合成本仅小幅下降3.11万元。

通过以上对系统运行经济性与环保性的分析结果可以得出，在系统中考虑CHWPPS能够有效提升可再生能源就地消纳能力，增加通道利用率，提高经济效益。同时，当系统中储能总装机容量增加时，可以在一定程度上缓解火电机组调峰压力，提高可再生能源渗透率，实现低碳经济调度。并且，3种场景下GCTMSA均能获得可行解，这说明本文所提算法的普适性。

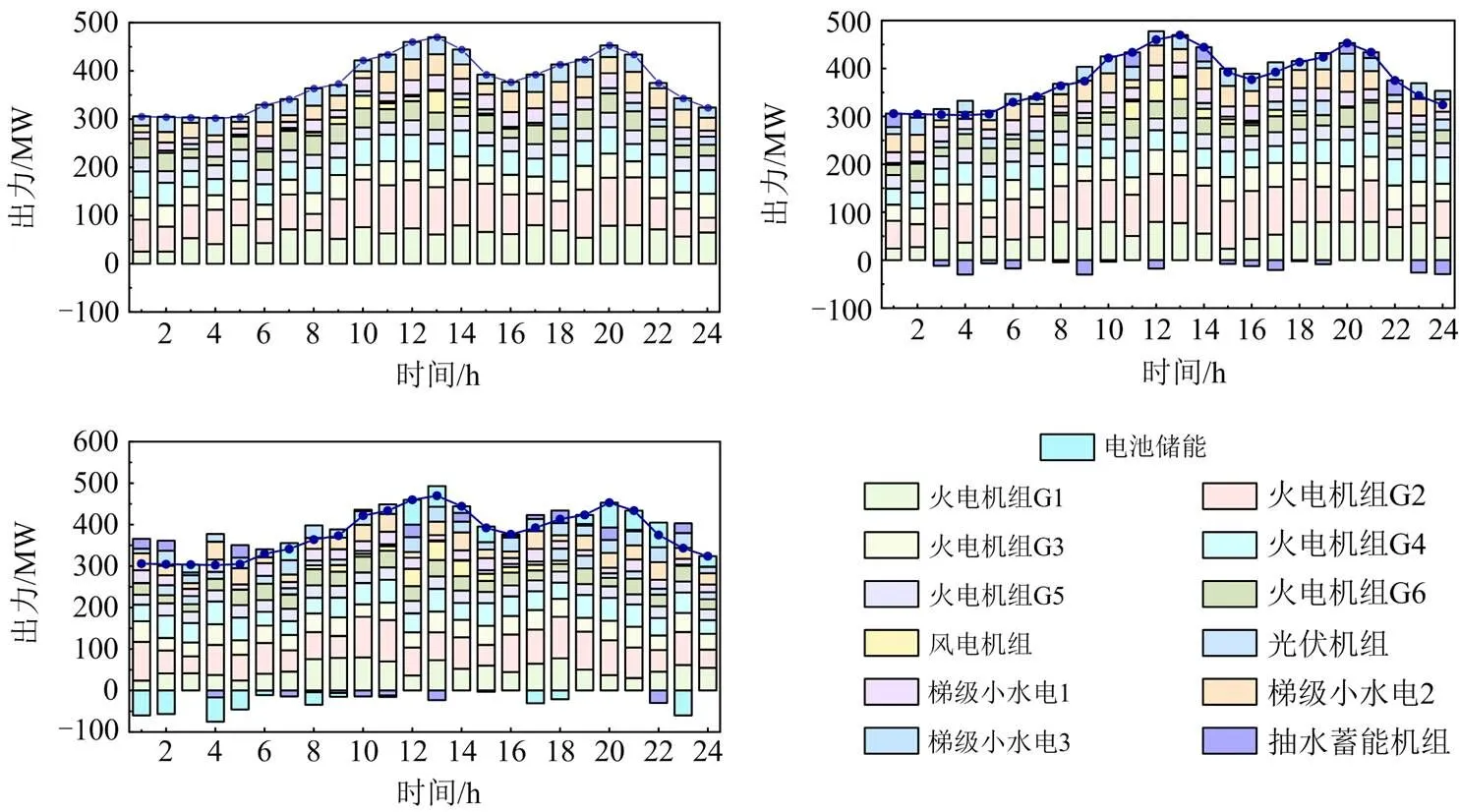
图6 各场景下日前优化调度

2) 不同算法下的求解结果分析

借助GCTMSA、粒子群算法(particle swarm optimization, PSO)、遗传算法(genetic algorithm, GA)和生物地理算法(biogeography-based optimization, BBO)分别对场景3下含CHWPPS的梯级水火风光蓄储联合调度模型进行求解寻优，为避免算法求解的随机性，每种算法均独立运行30次，统计所得最小值、最大值、均值及方差结果如表3所示。并将各算法独立运行30次求解结果的最大值、最小值和平均值作为评价算法搜索能力的指标，方差作为判别算法求解稳定性的指标。

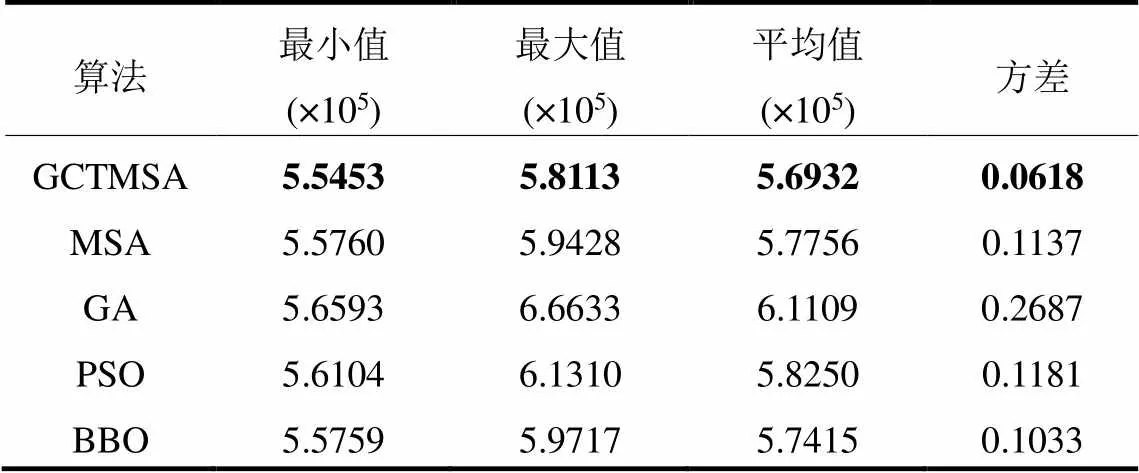
表3 不同算法的统计结果

从表3中可以确认，GCTMSA独立运行30次的最小值、最大值、平均值在所有算法中均为最小，其最小目标值相较于MSA、GA、PSO和BBO算法分别降低了0.307万元、1.14万元、0.651万元和0.306万元，最大值分别降低了1.316万元、8.586万元、3.197万元和1.604万元，平均值分别降低了0.824万元、4.177万元、1.318万元和0.483万元。此结果综合说明了GCTMSA在种群多样性上明显优于其他算法，且能搜索到更小的综合成本，具有较强的寻优能力。

并且，在所有算法求解结果中，GCTMSA的最大值和最小值差值最小，为2.66万元，且其能取得最低的方差。GCTMSA独立运行30次求解结果的方差相较于MSA、GA、PSO和BBO算法分别降低了45.6%、77.0%、47.7%和40.2%，表明了GCTMSA求解结果的稳定性。此外，为了直观地观察各算法求解结果的分布情况，借助图7所示的箱线图将各算法独立运行30次求解所得综合成本值可视化。由图7可知，相较于其他优化算法，GCTMSA所对应的箱体最扁、端线最短，中位数值和均值也是所有算法中最小的，说明GCTMSA独立运行30次所获得的综合成本值分布最为集中，波动最小，具有更优越的稳定性。

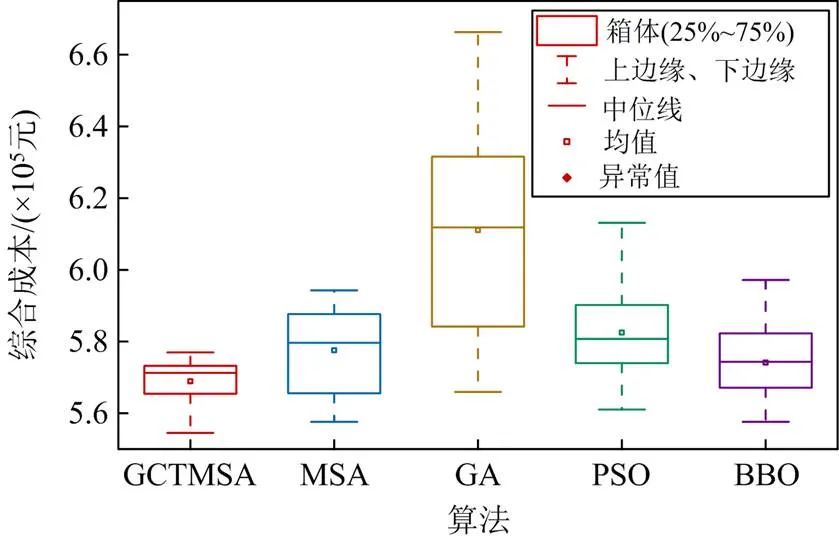
图7 运行30次的综合成本值分布1

与此同时，图8展示了所有算法独立运行30次的收敛曲线。由图8可以看出，GCTMSA相较于其他算法，下降速度更快，当迭代次数相同时，GCTMSA具有更低的目标适应值，收敛更为迅速，GCTMSA在不到200次迭代次数内收敛并取得更低的全局目标函数值，而MSA、GA、PSO和BBO算法均出现陷入局部最优的情况，其收敛迭代次数均大于200次。此结果进一步验证了所提算法寻优速度的优越性。

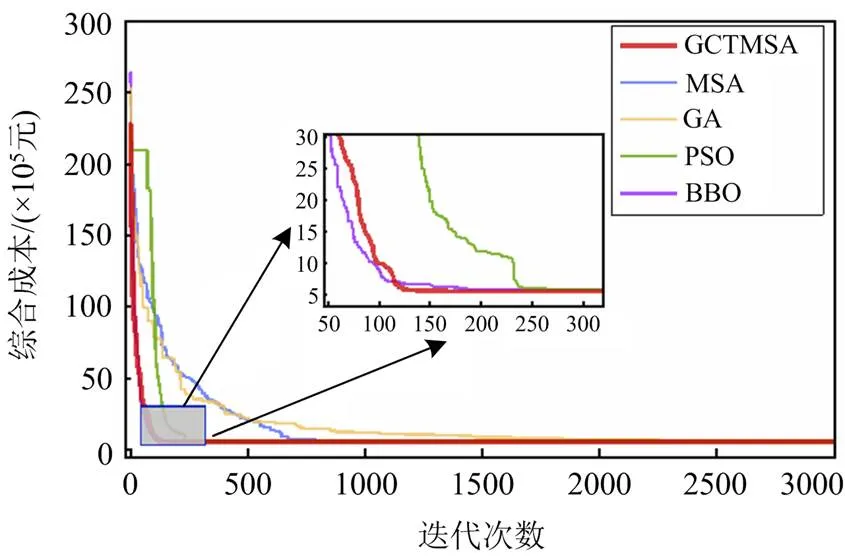
图8 所有算法的收敛曲线1

3.2 省域简化电力系统仿真

为了进一步验证本文所提方法与模型在实际系统中的有效性和优越性，在中国某省简化电网系统上展开算例分析，系统接线图如图9所示。其中包括9台火力发电机组，总装机容量为10 730 MW。在节点11接入一台装机容量为900 MW的电池储能机组，其充放电功率为±250 MW，充放电效率为0.9。分别在节点3和节点10接入3个CHWPPS电站，包含HJD、DF、SFY 3台水电站组成的梯级水电站群及其周边3台风电机组、3台光伏机组、3台抽蓄机组，梯级水电站总装机容量为1895 MW，每台抽水蓄能电站抽水功率和放电功率均为253 MW。光伏数据收集自文献[7]中节点4处平均出力，典型日负荷及光伏出力曲线如图10所示，风速数据见文献[7]，弃风弃光惩罚系数为500元/MWh，其他参数设置与IEEE 6机30节点中设置相同。

图9 一个简化的省域电网系统

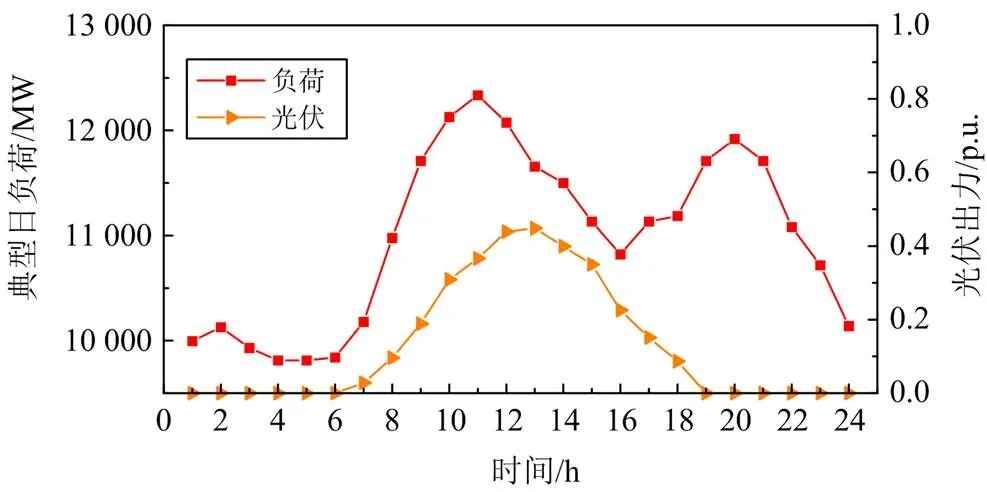
图10 典型日负荷及光伏出力曲线2

1) 不同场景下的结果分析

借助GCTMSA仿真所得不同场景下的优化结果如表4所示。场景设置与IEEE 6机30节点系统相同。

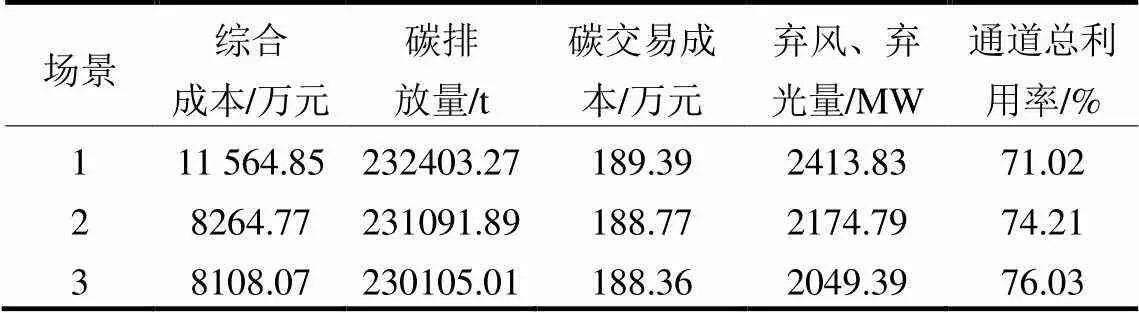
表4 各场景下结果参数比对2

由表4可知，本文场景3下各优化结果均优于其他两种场景。尤其是在综合总成本方面，场景2比场景1降低了28.5%。通道容量从71.02%提升到了74.21%，弃风弃光量降低了239.04 MW，这再次验证了CHWPPS对提升系统能源利用率与经济效益的有效性。其次，对比场景2和场景3下实验结果可以发现，在系统中接入具有灵活调节能力的储能机组，能迅速反应负荷需求，弃风弃光量从场景2的2174.79 MW减少到了2049.39 MW，通道利用率提升了2.45%。由于储能自身存在损耗，综合成本小幅度减少了156.70万元，碳排放量从2 231 091.89 t减少到了230 105.01 t。进一步为系统低碳经济运行创造条件。

2) 不同算法下的求解结果分析

将GCTMSA与传统MSA、GA、PSO和BBO算法分别独立运行30次的求解结果进行比较，统计结果如表5所示。

表5 不同算法的统计结果2

由表5可知，在30次独立运行中，GCTMSA在最小值、最大值、平均值方面均优于其他算法。GCTMSA搜索获得了综合成本最小值，为8052.8万元，其次综合成本最小值由BBO获得，为8062.2万元，GCTMSA比 BBO求解所得综合成本最小值结果降低了9.4万元。值得注意的是，在实际系统中，由于机组数量较多，GA和PSO算法求解存在较大的随机性，存在无法求出最优值的情况，最大值分别为23 702万元和32 502万元，而GCTMSA相对稳定，目标函数最大值和最小值差值仅为240万元。并且，图11展示了将GCTMSA、MSA、GA、PSO、BBO分别独立运行30次求解结果的分布情况。

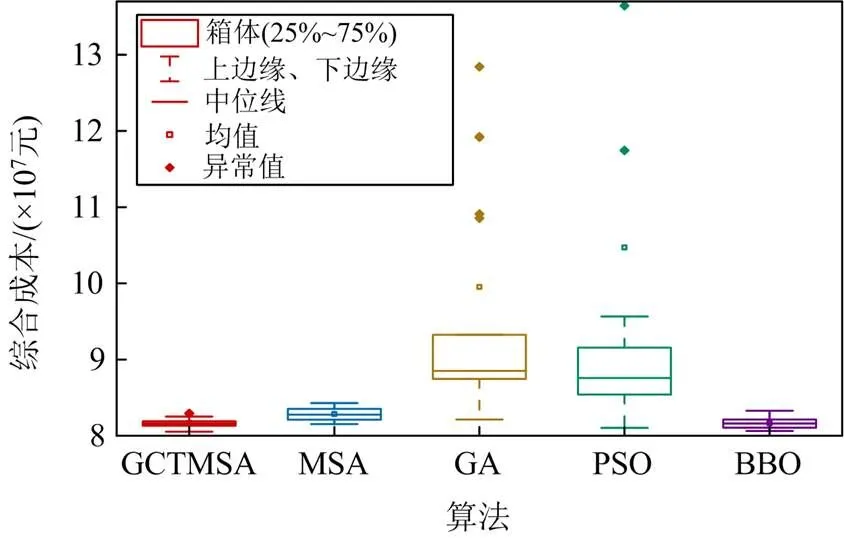
图11 运行30次的综合成本值分布2

综合图11中各算法分别独立运行30次求解结果的分布情况和表5的方差值可知，相较于MSA、GA、PSO、BBO，GCTMSA对应的箱体最扁，上下边缘间隔最近，中位数值和均值均是所有算法中最小的，且其方差相较于其他算法，最大减少了5.098。进一步验证了本文所提算法GCTMSA求解的稳定性。值得一提的是，GCTMSA在收敛特性方面相较于其他算法也表现优越。观察图12可知，GCTMSA在迭代初期下降明显，且在迭代次数相同时，能取得更低的目标值。

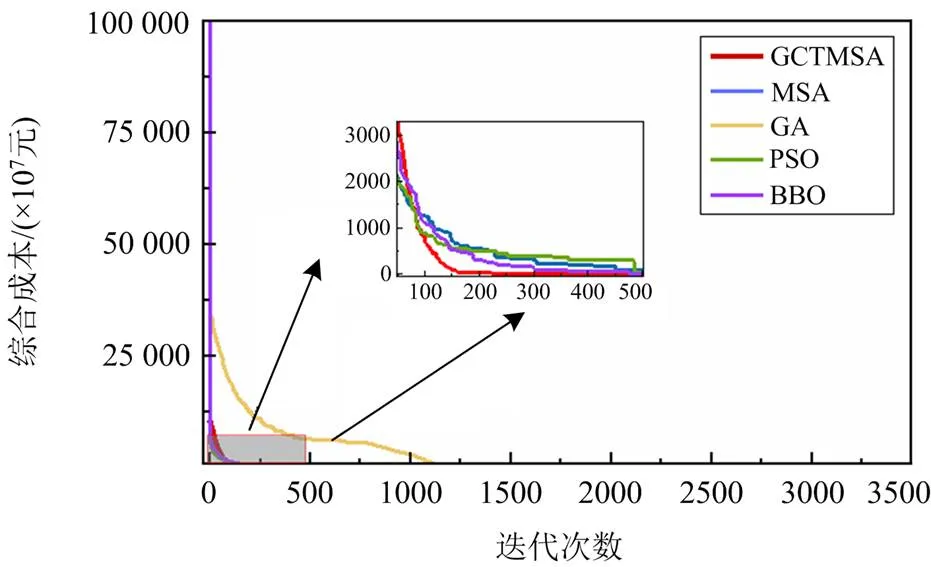
图12 所有算法的收敛曲线2

4 结论

针对新型电力系统中多能互补调度问题，本文从模型与求解方法两方面开展了研究，构建了一个含CHWPPS的梯级水风光蓄储联合调度模型，并提出了一种基于贪婪策略、自适应交叉算子和自适应t分布的GCTMSA算法。在一个修改的IEEE 6机30节点系统和一个省域简化电力系统中开展了仿真实验，一些讨论和结论如下：

1) 本文构建的含CHWPPS的梯级水火风光蓄储联合调度模型，能充分挖掘抽蓄和储能的灵活能力，有效提升新能源消纳能力，提高现有水电通道利用效率，为多能互补调度技术发展提供参考。

2) 本文所提GCTMSA算法相较于MSA、GA、PSO和BBO算法，在两个系统中搜索所得综合成本最大分别减少了1.14万元和158.88万元，方差分别降低了0.2069和5.098。这表明了GCTMSA求解含CHWPPS的梯级水风光蓄储联合调度系统时，能搜索到更为低碳经济的调度策略，稳定性更好，求解速度更快。

[1] JURASZ J, CANALES F A, KIES A, et al. A review on the complementarity of renewable energy sources: concept, metrics, application and future research directions[J]. Solar Energy, 2020, 195: 703-724.

[2] 黎博, 陈民铀, 钟海旺, 等. 高比例可再生能源新型电力系统长期规划综述[J/OL]. 中国电机工程学报: 1- 27[2022-04-03]. https://doi.org/10.13334/j.0258-8013. pcsee.212716.

LI Bo, CHEN Minyou, ZHONG Haiwang, et al. A review of long-term planning of new power systems with large share of renewable energy[J/OL]. Proceedings of the CSEE: 1-27[2022-04-03]. https://doi.org/10.13334/j.0258- 8013.pcsee.212716.

[3] 冯奕, 应展烽, 颜建虎. 考虑碳排放成本的多能互补微能源网储能装置优化运行[J]. 电力系统保护与控制, 2021, 49(8): 92-99.

FENG Yi, YING Zhanfeng, YAN Jianhu. Optimized operation of energy storage in a multi-energy complementary micro-energy network considering carbon emission cost[J]. Power System Protection and Control, 2021, 49(8): 92-99.

[4] BERAHMANDPOUR H, KOUHSARI S M, RASTEGAR H. A new flexibility based probabilistic economic load dispatch solution incorporating wind power[J]. International Journal of Electrical Power & Energy Systems, 2022, 135.

[5] TANG Y, FANG G, TAN Q, et al. Optimizing the sizes of wind and photovoltaic power plants integrated into a hydropower station based on power output complementarity[J]. Energy Conversion and Management, 2020, 206.

[6] YANG H, LIANG R, YUAN Y, et al. Distributionally robust optimal dispatch in the power system with high penetration of wind power based on net load fluctuation data[J]. Applied Energy, 2022, 313.

[7] HUANG Q, HAN S, RONG N, et al. Stochastic economic dispatch of hydro-thermal-wind-photovoltaic power system considering mixed coal-blending combustion[J]. IEEE Access, 2020, 8: 218542-218553.

[8] 臧紫坤, 杨晓辉, 李昭辉, 等. 考虑储热改造与最优弃能的风光火储低碳经济调度[J]. 电力系统保护与控制, 2022, 50(12): 33-43.

ZANG Zikun, YANG Xiaohui, LI Zhaohui, et al. Low-carbon economic scheduling of solar thermal storage considering heat storage transformation and optimal energy abandonment[J]. Power System Protection and Control, 2022, 50(12): 33-43.

[9] BASU M. Multi-region dynamic economic dispatch of solar-wind-hydro-thermal power system incorporating pumped hydro energy storage[J]. Engineering Applications of Artificial Intelligence, 2019, 86: 182-196.

[10] 臧海祥, 马铭欣, 周亦洲, 等. 电力市场环境下风电-光热-生物质混合电站鲁棒优化调度模型[J]. 电力系统保护与控制, 2022, 50(5): 1-11.

ZANG Haixiang, MA Mingxin, ZHOU Yizhou, et al. Robust optimal scheduling model for a ’wind power- concentrating solar power-biomass’ hybrid power plant in the electricity market[J]. Power System Protection and Control, 2022, 50(5): 1-11.

[11] SAKTHIVEL V P, SATHYA P D. Single and multi-area multi-fuel economic dispatch using a fuzzified squirrel search algorithm[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 1-13.

[12] HINDI K S, AB GHANI M R. Dynamic economic dispatch for large scale power systems: a Lagrangian relaxation approach[J]. International Journal of Electrical Power & Energy Systems, 1991, 13(1): 51-56.

[13] GRANELLI G P, MARANNINO P. Fast and efficient gradient projection algorithm for dynamic generation dispatching[J]. IEE Proceedings. Part C, 1989, 136(5): 295-302.

[14] DENG Z, YANG J, DONG C, et al. Research on economic dispatch of integrated energy system based on improved krill swarm algorithm[J]. Energy Reports, 2022, 8: 77-86.

[15] YANG W, PENG Z, YANG Z, et al. An enhanced exploratory whale optimization algorithm for dynamic economic dispatch[J]. Energy Reports, 2021, 7: 7015-7029.

[16] NADERI E, AZIZIVAHED A, ASRARI A. A step toward cleaner energy production: a water saving-based optimization approach for economic dispatch in modern power systems[J]. Electric Power Systems Research, 2022, 204.

[17] 张歆蒴, 陈仕军, 曾宏, 等. 基于源荷匹配的异质能源互补发电调度[J]. 电网技术, 2020, 44(9): 3314-3320.

ZHANG Xinshuo, CHEN Shijun, ZENG Hong, et al. Heterogeneous energy complementary power generation dispatching based on output-load matching[J]. Power System Technology, 2020, 44(9): 3314-3320.

[18] WANG G G. Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems[J]. Memetic Computing, 2018, 10(2): 151-164.

[19] FATHY A, ABD ELAZIZ M, SAYED E T, et al. Optimal parameter identification of triple-junction photovoltaic panel based on enhanced moth search algorithm[J]. Energy, 2019, 188.

[20] SUN S, SU Y, YIN C, et al. Optimal parameters estimation of PEMFCs model using converged moth search algorithm[J]. Energy Reports, 2020, 6: 1501-1509.

[21] FENG Y, WANG G G. A binary moth search algorithm based on self-learning for multidimensional knapsack problems[J]. Future Generation Computer Systems, 2022, 126: 48-64.

[22] 殷自力, 陈宇星. 基于功率传输转移分布因子的简化电网潮流计算方法[J]. 电力系统保护与控制, 2016, 44(17): 25-30.

YIN Zili, CHEN Yuxing. A power flow computation method for reduction grid based on power transfer distribution factor[J]. Power System Protection and Control, 2016, 44(17): 25-30.

[23] MENÉNDEZ J, FERNÁNDEZ-ORO J M, GALDO M, et al. Efficiency analysis of underground pumped storage hydropower plants[J]. Journal of Energy Storage, 2020, 28.

[24] 刘芸, 韩松, 黄秋立. 考虑火电深度调峰煤耗特性的随机机组组合[J]. 计算机仿真, 2021, 38(2): 67-71, 86.

LIU Yun, HAN Song, HUANG Qiuli. Stochastic unit commitment considering coal consumption of thermal units under deep peak regulation[J]. Computer Simulation, 2021, 38(2): 67-71, 86.

[25] WANG G G, GUO L, GANDOMI A H, et al. Chaotic krill herd algorithm[J]. Information Sciences, 2014, 274: 17-34.

Dispatch of a cascade hydro-thermal-wind-photovoltaic-storage complementary system based on GCTMSA

CAO Yun, HAN Song, RONG Na, ZHAN Xianwen, LIU Min

(College of Electrical Engineering, Guizhou University, Guiyang 550025, China)

To develop novel theories and methods of power system dispatch, this paper constructs a hydro-thermal-wind- photovoltaic-storage coupled dispatching system, one that integrates cascade hydro-wind-photovoltaic-pumped storage (CHWPPS). When analysing such a coupled dispatching system, it is easy for the traditional solution method to fall into a local optimum and it is challenging to arrive at a feasible solution within a satisfactory time. This paper proposes a greedy strategy, adaptive crossover operator and adaptive t-distribution variation-based moth search algorithm (GCTMSA) to overcome these shortcomings. GCTMSA combines the adaptive crossover operator with the Lévy flight strategy, introduces an adaptive t-distribution variation in flight straight strategy, and uses the greedy strategy to enhance the global search capability and speed. The case studies conducted on a modified IEEE 6-machine and 30-bus system and a provincial simplified power system show that the GCTMSA has more substantial search capability and stability than the traditional moth search, genetic or particle swarm algorithms, as well as biogeography-based optimization. The impact of CHWPPS and battery storage on the system is analyzed. The related discussion and conclusion can provide a reference for developing multi-energy complementary technologies such as dispatching hydro-thermal-wind-photovoltaic-storage coupled systems.

CHWPPS; self-adaptive crossover operator; adaptive t-distribution; greedy strategy; GCTMSA

10.19783/j.cnki.pspc.220475

国家自然科学基金项目资助(51967004)；贵州省优秀青年科技人才项目资助(黔科合平台人才[2021]5645)；贵州省科学技术基金项目资助(黔科合基础[2021]277)；贵州省教育厅批准建设“新型电力系统及其数字化技术工程研究中心”(黔教技[2022]043号)

This work is supported by the National Natural Science Foundation of China (No. 51967004).

2022-04-05；

2022-07-10

曹 韵(1999—)，女，硕士研究生，研究方向为电力系统与综合能源；E-mail: 1726454513@qq.com

韩 松(1978—)，男，通信作者，博士，硕士生导师，研究方向为交直流电力系统动态分析、新型电力电子装备以及配电网规划。E-mail: shan@gzu.edu.cn

(编辑 魏小丽)