基于零序分量的风电场集电线不对称接地故障定位

朱永利，丁 嘉，潘新朋

基于零序分量的风电场集电线不对称接地故障定位

朱永利，丁 嘉，潘新朋

(华北电力大学电气与电子工程学院，河北 保定 071003)

风电场集电线上并接电源多、电源故障特性复杂，其故障定位问题持续困扰风电运营商。为此提出一种基于零序分量的集电线不对称接地故障新型定位方案。在定义无分支区域的基础上，充分考虑风机与风电场零序分量之间的特殊关系，分层实现风机无关的故障无分支区域识别与故障测距。首先，引入无分支区域状态信息的概念以反映零序电流主流通路径，通过状态信息的优化匹配识别故障无分支区域。然后，从零序阻抗出发推导故障无分支区域测距模型，并将其转化为优化问题实现故障距离求解。所提方案在较少测点下即可完全消除风机影响，并能有效适用于含分支集电线，同时无需数据严格同步，测距不会出现多解。最后，还设计了线路参数在线计算方案应对线路参数变化问题。仿真结果表明，所提方案较为准确，性能不受风机、故障位置、故障类型、过渡电阻以及数据不同步影响，整体性能优于现有方案。同时也验证了线路参数在线计算的有效性。

风电场；集电线；不对称接地故障；故障定位；零序分量

0 引言

构建以新能源为主体的新型电力系统已被提上日程，风电作为一种典型新能源电能，必将成为新型电力系统的重要组成部分。我国风电场往往地处荒山、戈壁、草原和近海，运行环境复杂，场内线路故障几率大[1-2]，若不能及时确定集电线故障位置并加以排除，会造成长时间的弃风现象[2]。因此，发展可靠有效的风电场集电线故障定位技术对于改善风电场运行、促进新型电力系统建设意义重大。

国内外输配电网的故障定位技术主要包括行波法[3-7]、故障分析法[8-10]、人工智能法[11-13]等。然而，集电线结构较为特殊(接入电源众多、电源故障特性复杂)，现有输配电网的定位方法难以使用[1]，即使是有源配电网的定位方法也不易应对。因此，目前集电线故障定位仍是一个难题，国内外有关研究成果较为有限且存在不足。

文献[1]提出一种风电场集电线行波测距方法，针对所有测点建立行波传输方程，构建行波传输方程组，然后引入基于冗余度的统计学参数估计方法成功实现故障测距，但是集电线上大量的风机会使得行波折反射频繁，故障行波的识别难度较大。文献[2]将行波法应用到集电线的各个区段(相邻风机之间为一个区段)，消除了风机频繁折反射对行波法的影响，但是大量的风机将集电线划分成了众多区段，因此方案所需测点的数目甚至远多于风机数目，并且由于相邻风机间距较小，这也增大了行波传播时间的测量误差。

风电场中故障分析法的应用难点主要在于风机故障特性复杂且难以表征，对其描述不准确会降低方案性能。文献[14]引入含风机的短路计算方法，通过评估模拟故障下含风机短路计算结果与实际故障下所测电气量之间的差异实现了集电线故障区段的识别。但是，由于含风机短路计算的精确性问题以及模拟故障点有限，该方案只能实现区段定位，同时其同样需要较多测点。文献[15]近似认为各风机提供的故障电流相等，进而通过对这一电流的估计改进了传统阻抗法，削弱了风机的影响。文献[16-17]为完全消除风机对故障分析法的影响，在相邻风机之间进行单端阻抗法故障测距与故障区段判断，但是同文献[2]一样，这两种方案也需在每一区段安装测点，测点数量需求过大。

文献[18-19]采集集电线首端的电压电流相量构建数据集，分别应用极限梯度提升算法、长短期记忆神经网络建立回归模型实现集电线故障测距，避免了复杂的含风机故障分析过程，但是，算法性能、输入量包含的故障信息丰富与否都会对人工智能方案的定位效果产生影响，因此在算法类型与输入量的选择上还有待进一步研究。

集电线故障定位技术所面临的关键问题除了以上提及的风机影响、测点数目以外，还有含分支集电线的适用性问题。因为从工程实际可知，集电线有时会含有一些线路分支。但是，文献[1-2,14,17-19]都没有考虑到此问题，文献[15-16]则是采用人工排查或测点的大规模安装来解决这一问题。

由于实际运行中线路不对称接地故障占比最大，单相接地故障更是占八成左右[10,18]，因此本文针对集电线不对称接地故障，提出一种基于零序分量的故障定位方案。本文首先分析风电场不对称接地故障的故障特征，然后定义集电线无分支区域，基于优势特征构建风机无关的两层定位方案。层次一引入无分支区域状态信息的概念，优化匹配两种方式所得状态信息，识别故障无分支区域；层次二针对所得的故障无分支区域，推导基于零序阻抗的故障测距模型，采用优化思想求解故障距离，最终完成定位。另外，本文还设计了辅助定位的线路参数在线计算方案。最后，在PSCAD/EMTDC中搭建仿真模型验证方案性能，并与现有技术进行对比。

1 风电场不对称接地故障特征分析

1.1 风电场拓扑

风电场的一般拓扑结构如图1。在风电场中，所有风电机组均经箱式变压器(简称箱变)与集电线相连；集电线位于主变压器(简称主变)35 kV侧，经主变升压至110 kV或220 kV后与系统相连。

图1 风电场一般拓扑结构

相较于一般电网，风电场拓扑的主要特点如下。1) 出于风电场安全性、可靠性考虑，目前风电场均接地，且主要采用经小电阻接地的方式[15,20]。2) 为了阻隔风机零序电流、抑制谐波注入电网，箱变高压侧采用三角形接线[15,20-21]。3) 为充分利用各处风能，集电线会通过多点连接风机，从而形成了多电源辐射型网，并且集电线所连接电源数目要远多于常规电力线路，这也使得相邻电源之间距离较近。4) 集电线上电缆、架空线并存[1,14]，风机箱变与架空线之间、架空线与母线之间存在较短电缆[14]。

1.2 故障特征分析

风电场属于中性点经小电阻接地系统，在出现接地故障时会形成有效的电流回路，具备阻抗法测距条件[15]，而且相较于中性点不接地系统与谐振接地系统，小电阻接地系统在不对称接地故障下零序电流更大，因此已有研究针对小电阻接地系统提出基于零序电流的保护[22]与故障识别[23]方案。另外，受风机转速、变流器控制策略的影响，故障期间风机的等效正负序阻抗都是不断变化的[24-25]，这使得风机正负序故障特征表现出较强的不确定性和复杂性，风电场正负序分量也因此呈现出不稳定性；相比之下，由于箱变三角形接线的阻隔，风电机组零序开路，因此其并不参与风电场零序网络的构成，不会对零序分量造成影响，风电场零序分量更加稳定。由以上分析可知，根据风电场零序分量实施故障定位更有优势，因此本文进一步分析风电场零序故障特征，构建基于零序分量的集电线故障定位方案。需要说明的是，由于风电场电缆较短，电缆故障率低，不对称接地故障少，所以本文只对架空线部分进行故障定位。

假设在图1所示风电场的集电线1上点出现不对称接地故障，可以绘制对应零序网络如图2。图中，集电线各部分线路的对地电容集中考虑。

图2 风电场零序网络

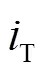
2 无分支区域的定义与定位方案的构建

由于风能分布不均等原因，风电场中一些集电线可能会包含若干分支，如图3所示。为高效准确地识别不同分支的故障，本文首先对含分支集电线进行划分。经划分后，集电线会被分为若干不含分支的区域，本文称其为无分支区域。

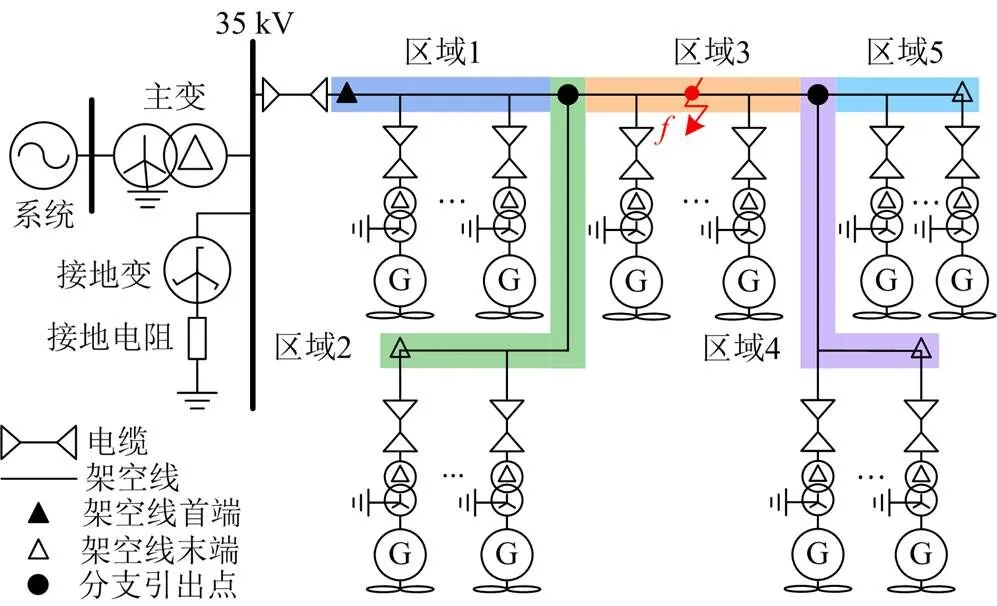
图3 含分支集电线结构示意图

集电线划分基于集电线拓扑结构实施，相邻无分支区域以分支引出点为分界点，如图3。分支引出点与相邻的架空线首端或末端之间、相邻两个分支引出点之间均为一个无分支区域。对于图3所示风电场，集电线可以被划分为图中5个无分支区域。采用以上划分方法所得到的子区域数目要远少于文献[2,16-17]中以风机引出点作为子区域分界点的划分方式，因此更有利于减少测点的安装数目。为了便于描述，后文所有无分支区域均简称为区域。

基于上述划分，本文设计两层定位方案。层次一用于识别故障点所在区域；层次二与层次一相级联，针对层次一所得故障区域实施故障测距，确定准确故障点。以上分层定位方案以层次一为基础，可以有效实现含分支集电线的故障定位，同时也有利于降低故障定位复杂度，提高定位效率。

3 故障无分支区域识别

3.1 无分支区域状态信息定义

假设图3中区域3上的点出现不对称接地故障，根据图3建立对应零序网络，如图4所示。

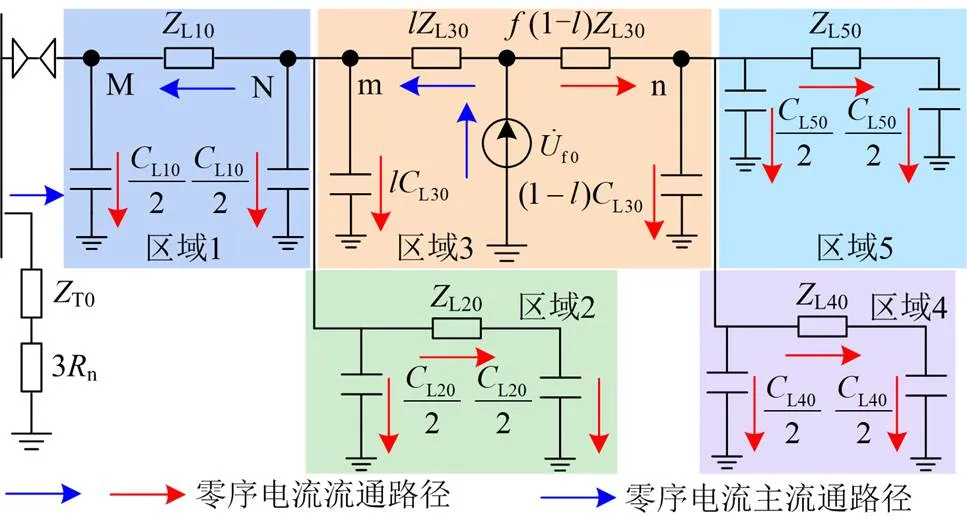
图4 含分支集电线零序网络示意图

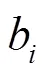
为实际确定各区域状态信息，可从零序电流主路径的本质出发，通过区域上零序电流的大小进行判断。获取故障集电线上所有区域首端的零序电流有效值，与预设阈值进行比较，大于或等于阈值时表明该区域位于零序电流主路径范围内；小于阈值时表明该区域位于零序电流主路径外。如前所述，主路径中零序电流远大于其他部分，并且主路径内部各处零序电流数值相近，因此上述阈值的设置并不困难。考虑到零序电流主路径一定包含架空线首端，因此将此阈值设置为故障后故障集电线上架空线首端(如图4中的M点)零序电流有效值的50%，后续仿真可验证这一比例的合理性。值得指出的是，以上判据的本质是比较故障后架空线首端与各区域首端零序电流的大小，同时由于故障集电线上架空线首端零序电流会随故障场景的变化而变化，因此这一阈值实际上是自适应的。

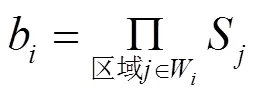
式中，||为“或”运算符。

在定义区域状态信息的基础上，本文通过优化匹配的方式构建目标函数实现故障区域识别。同时，优化方法的使用也能够增强识别方法的容错性。

3.2 故障区域识别目标函数的构建与求解

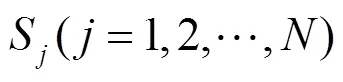
由工程经验可知，实际风电场中一条集电线所含分支并不会太多，远少于配电网，所以式(3)不会非常复杂，因此采用上述优化方法识别故障区域并不会耗费大量时间，同时二进制粒子群算法的性能也能够满足应用需求。

上述故障区域识别方法构成本文定位方案的层次一。对于不含分支的故障集电线，其本身即为唯一故障区域，因此可跳过该层次，直接执行层次二。

配电网中也存在基于优化匹配的定位方法[26]，但是其并不适用于集电线，因为其一般依靠故障相电流告警信息实现，而集电线并联电源过多、电源故障特征不确定性强，这使得故障相电流流通方向复杂，同时也可能给告警信息生成时所需阈值的整定带来困难。区别于这种配电网区间定位方法，本文从风电场零序电流较大的事实出发，结合集电线实际，基于零序电流进行故障区域识别，利用风机不提供零序电流的特征，使识别方法不需计及风机电源的影响，同时本文采用自适应阈值设计，保证了识别方法在小故障电流下的适用性。

4 故障无分支区域故障测距

4.1 故障测距模型构建

故障测距对结果准确性要求较高，因此本文在建立故障测距模型时保留线路零序对地电容，以尽可能提高等效模型精度。重画图4中故障区域(区域3)对应零序网络可得图5。

图5 故障区域零序网络示意图

由图5中线路m端的电气量可得式(4)。

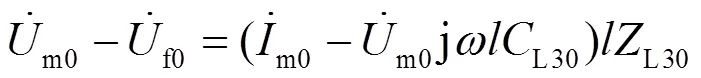
且由线路n端的电气量可得式(5)。

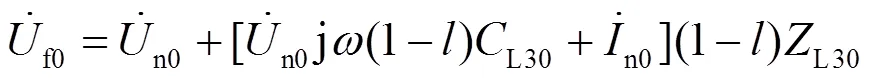
由于式(4)与式(5)所得故障点零序电压相等，因此有

式(6)含有多端电气量，若直接利用式(6)计算故障距离比，计算效果易受数据不同步问题的影响。为此，分别在式(6)等号两边取模值，可得到式(7)。

上述故障测距模型中双端量的利用使得过渡电阻的影响得以较好地消除。同时，该模型基于零序分量构建，而风电机组是零序开路的，因此风机对故障测距的影响得以克服。另外，计及线路分布电容也进一步提高了故障测距的精度。

4.2 故障测距模型求解

直接采用解析法求解式(7)时，须先对式(7)两边取平方，整理后可得形如式(8)的一元四次方程。

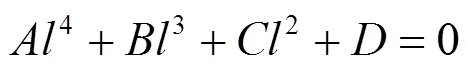
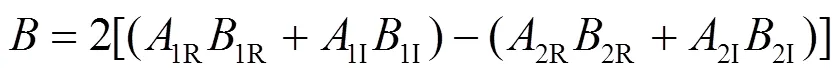
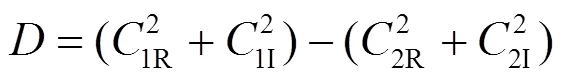
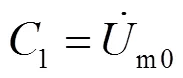
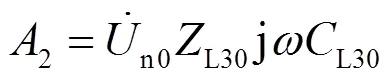
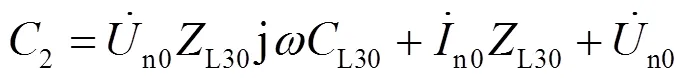
求解式(8)会得到多个解，仅依靠解的合理性，有时可能难以取舍。为解决以上问题，本文引入优化思想，根据式(7)构建用于方程求解的优化目标函数如式(19)，并采用标准粒子群算法(standard particle swarm optimization, SPSO)求解。

优化求解时，以式(19)作为适应度函数，通过最小化式(19)最终可以得到0~1之间唯一的最优实数解，克服了解析法求解时易出现解不唯一的缺点。以上测距方法构成本文定位方案的层次二。

5 线路参数在线计算方案

执行层次二时需要已知线路零序参数，但是这些参数可能会随气候、环境等因素的变化而变化，最终影响测距准确性。为解决这一问题，可以适时对线路参数进行在线计算，以更新参数预设值。

由前文可知，除首端区域(如图4中的区域1)外，含分支集电线上其他区域出现故障时，首端区域的全部线路总是被完全包含在零序电流主路径内。因此，可以借助首端区域的零序网络在线计算线路参数，来更新全风电场所有区域的参数预设值。

将图4中区域1的零序等效电路重画如图6。

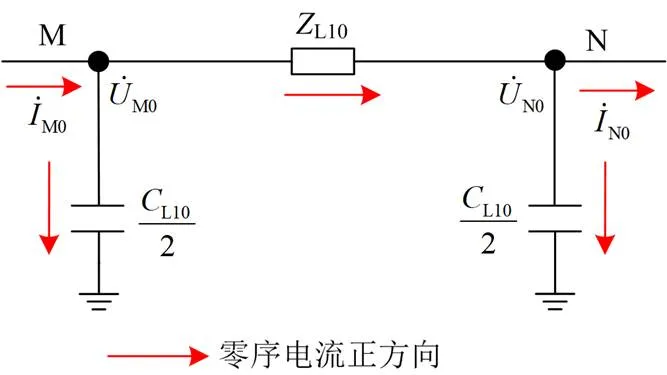
图6 集电线首端区域零序网络示意图

对于图6，可以建立如式(20)所示方程。

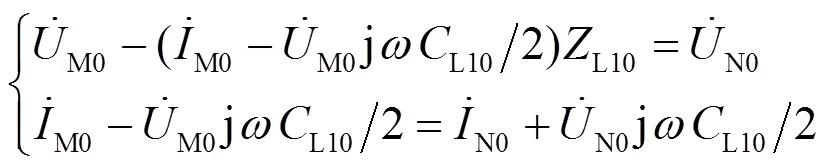
由式(20)可解得L10与L10，进而由式(21)可得单位长度架空线的零序阻抗与对地零序电容0、0。

式(21)所得为单位长度架空线的零序参数，将其与故障区域长度相乘即得式(19)所需线路参数。

实际上，参数计算无需在每次定位时都进行，其可以单独作为一个模块，设置为人工选择性投入，只需在参数长时间未更新时投入一次即可。当不含分支的集电线故障或层次一判断集电线首端区域为故障区域时，式(20)不成立，参数计算模块需要闭锁。另外，上述参数计算所需电压电流与集电线首端区域故障测距所需电压电流相同，因此不需再增加测点。需要指出的是，虽然参数计算对同步精度要求较高，但是也只需在参数计算相关测点安装少数几台高精度同步相量测量装置即可。由于本文故障定位方案无需数据严格同步，因此其余测点并不需要较高的同步精度。进一步，若风电场环境稳定，既有参数不易变化，也可不引入参数计算模块，也就无需安装较高精度的同步相量测量装置。

至此，可以给出风电场集电线不对称接地故障定位方案(含线路参数在线计算)的整体流程图，如图7所示。方案启动后，对于含分支故障集电线，首先根据零序电流确定区域状态信息，优化式(3)，识别故障区域；然后，优化式(19)，求解故障区域故障测距模型，得到故障距离；若有线路参数计算需求，且集电线首端区域并非故障区域，则先投入参数在线计算模块再执行层次二。对于不含分支故障集电线，直接执行层次二即可。由于风电场集电线在靠近母线处安装有零序电流保护等[20,28]，因此本文方案可以在保护动作、断路器跳闸后启动，获取跳闸前相关数据，经去噪、滤波处理后进行定位。

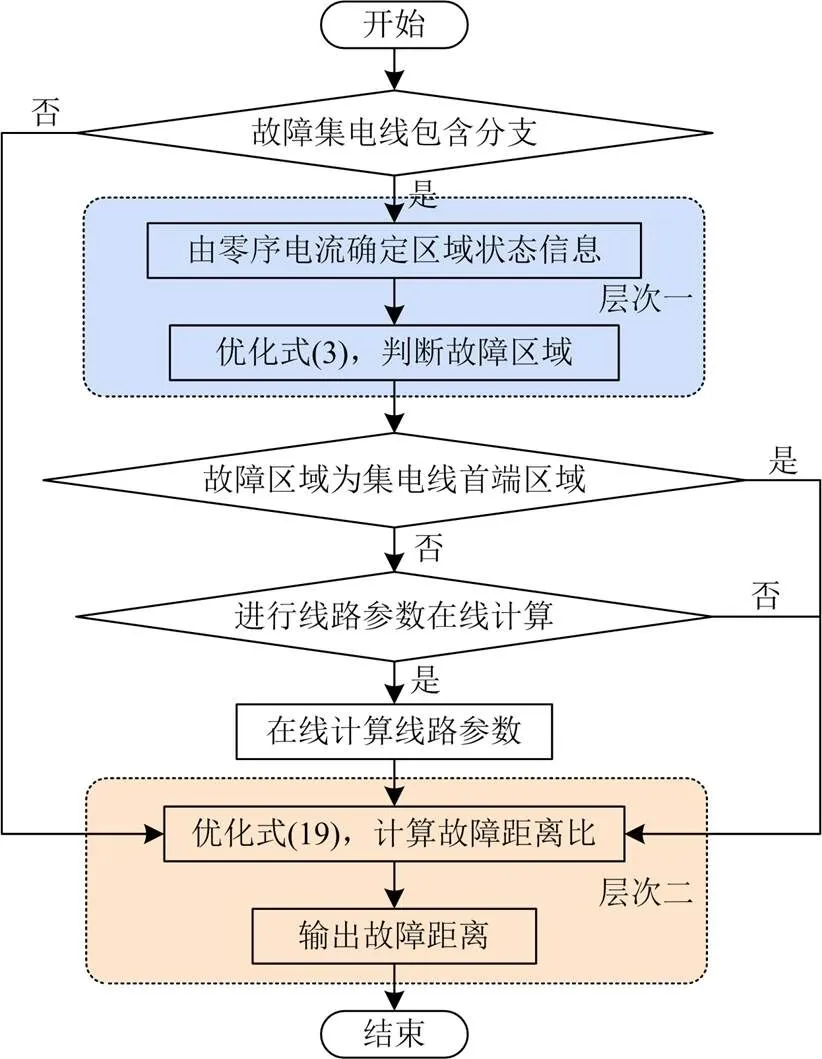
图7 故障定位方案流程图

6 仿真验证

为验证以上方案的性能，根据内蒙古某风电场实际结构，采用PSCAD/EMTDC建立仿真模型。在模型中，集电线1按照原有结构搭建，其他集电线做出一定简化以减轻仿真压力，仿真模型如图8。

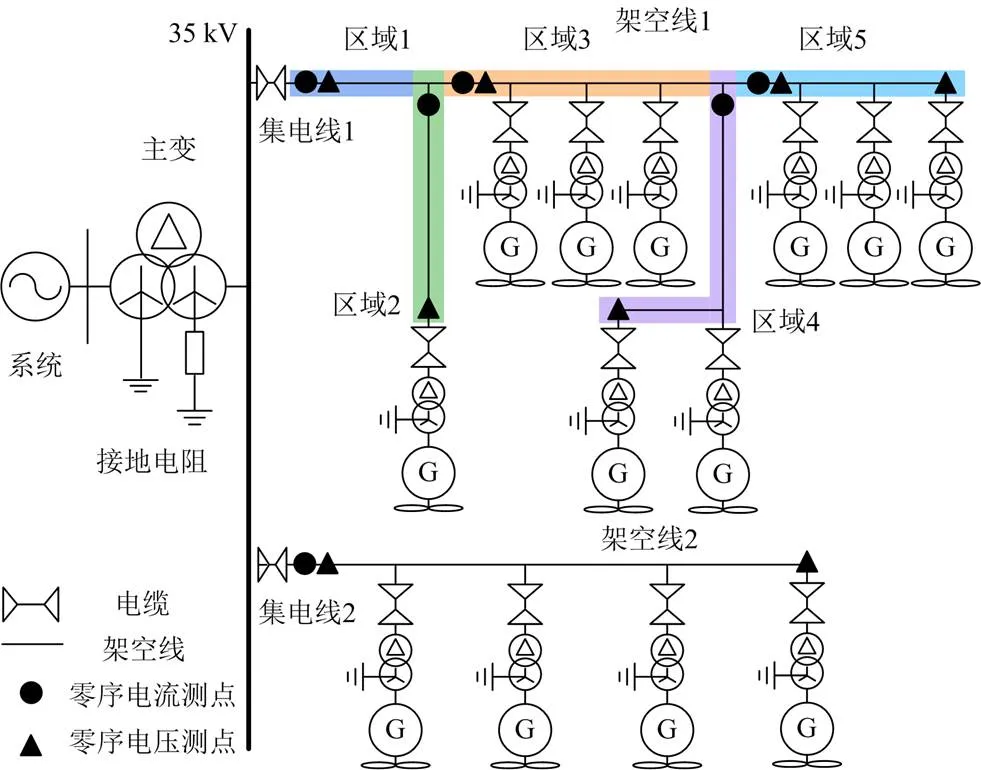
图8 仿真模型

图8所示仿真模型共包含两条集电线，分别为集电线1、集电线2，两条集电线所包含的架空线分别记作架空线1、架空线2。架空线1包含有多条分支，因此按照前文集电线划分方法将其划分为区域1—区域5。架空线1各区域以及架空线2的长度如表1所示，相应参数如表2；在PSCAD仿真中架空线采用分布参数模型。该风电场在主变中压侧经小电阻接地，主变接地电阻为67.3W。风机共有14台，均采用PSCAD双馈风机模型，额定容量均为2 MW。按照前文所述测点配置原则可得此风电场测点配置如图8所示，设置测点采样频率为1600 Hz。层次一所用BPSO算法参数设置如下：最大迭代次数为200，种群规模为100，学习因子均为2.5，加权系数为0.4，粒子速度变化范围为[-4, 4]；层次二所用SPSO算法参数设置如下：最大迭代次数为400，种群规模为100，学习因子均为2，加权系数采用线性递减权值策略随迭代变化，最大、最小加权系数分别为0.9、0.4，粒子位置变化范围为[0, 1]，粒子速度变化范围为位置变化范围的20%。

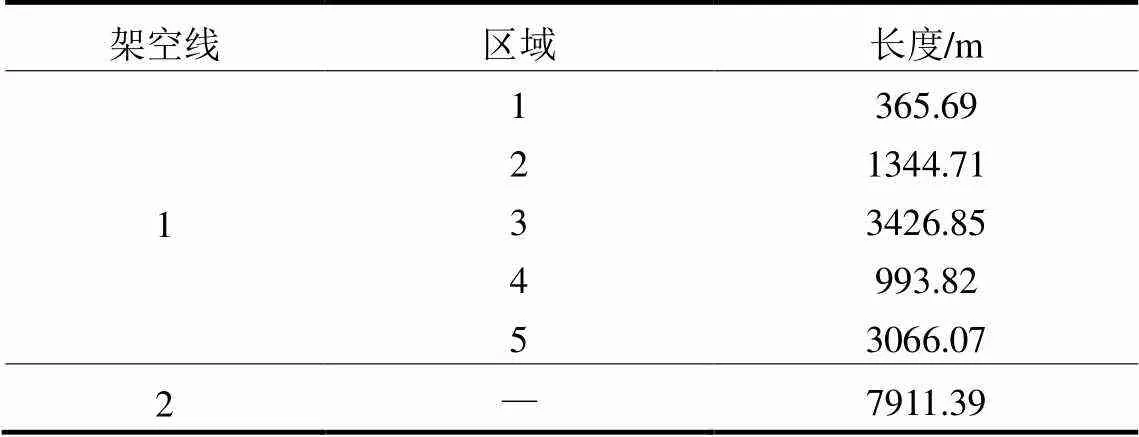
表1 架空线长度

表2 架空线参数

本文模拟不同故障场景，首先验证所提定位方案对于不同位置不对称接地故障的有效性，然后分析过渡电阻、风机容量、数据不同步以及线路参数变化对定位方案性能的影响，最后与现有方法进行比较。后文测距误差均为所得故障距离与实际故障距离之差比上实际故障距离。

6.1 不同位置的不对称接地故障

以A相接地、AB相接地为例，在同一集电线的不同区域、不同集电线上分别设置故障，过渡电阻均为0 Ω，风机容量均为2 MW。应用所提定位方案实施定位。其中，当集电线1的区域3上距区域3首端2026.22 m处出现A相接地时，架空线首端零序电压、零序电流的有效值波形如图9(故障时刻为18点处)，BPSO、SPSO优化所得适应度值变化曲线如图10。所有故障对应故障区域识别结果汇总如表3，测距结果与定位总用时汇总如图11。

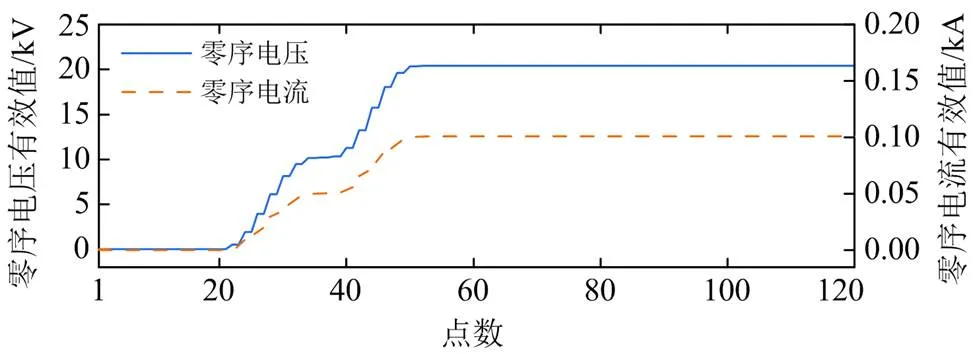
图9 零序电压、零序电流波形图

由图9及表3可以看到，当集电线出现不对称接地故障时，风电场会出现较为明显的零序分量。并且，当不同位置出现单相接地时，零序电流主路径内部各区域的首端零序电流总是很大，即使是内部各区域首端零序电流的最小值也远大于外部各区域首端零序电流的最大值。与单相接地相比，出现两相接地时，主路径内部零序电流减小，这主要与风电场各序阻抗的大小关系有关。但是，对于不同位置的两相接地，零序电流主路径内部区域的首端零序电流仍然远大于外部。以上现象表明，对于不同位置不对称接地故障，零序电流主路径总是非常明显，验证了前文对于风电场故障特征的分析。

图10 BPSO、SPSO适应度值变化曲线

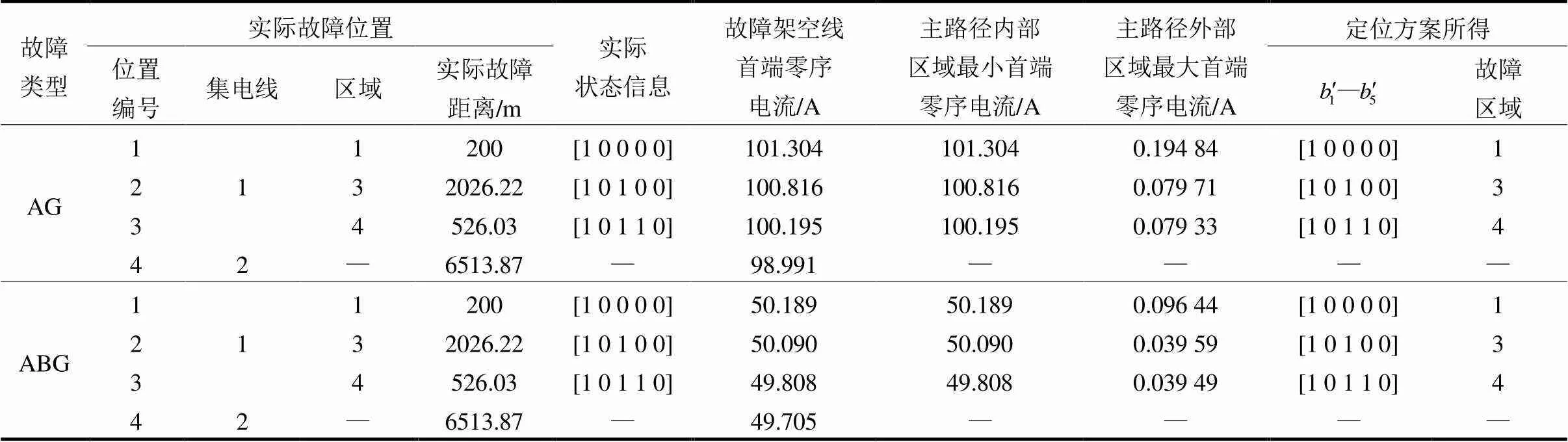
表3 不同位置故障时故障区域的识别

图11 不同位置故障时的测距误差与定位总用时

由表3还可以看到，尽管不同位置出现不同类型不对称接地故障时零序电流的大小存在差异，但是层次一中区域状态信息的确定以及故障区域的识别并没有受到影响。其原因在于，本文在确定区域状态信息时采用了自适应阈值；同时，层次一所利用的实质上是零序电流的分布特征，即零序电流主路径内外的零序电流大小差异。因此，层次一的识别效果与零序电流的绝对大小无关。

完成故障区域识别后，采用层次二进行故障测距。由图11可知，对于不同位置不对称接地故障，层次二测距误差均在0.6%以内，这主要得益于层次二基于零序网络建立，完全消除了风机的影响。

另外，图11还给出了在AMD Ryzen 7 4800H 2.90 GHz CPU的Matlab2020环境下本文定位方案的耗时情况。能够看到，尽管集电线1需要先识别故障区域导致耗时大于集电线2，但是最长耗时也仅有0.6 s。这表明优化算法的引入并没有为定位方案带来较大的时间成本。同时，由图10所示适应度值变化曲线可知，BPSO、SPSO均能可靠、迅速收敛(因为按照本文区域划分方法所得区域数目有限，所以图10中BPSO在初次迭代就得到最优解，使得适应度值恒为理论最小值0.8)，综合以上分析，并结合表3、图11准确的定位结果可知，本文所采用优化算法的性能能够满足需要。

6.2 过渡电阻对定位方案的影响

在集电线1的区域3上设置A相、AB相接地故障，故障点距区域3首端2026.22 m，过渡电阻分别设置为0、50、100、200、300W，风机容量为额定值，所得故障区域识别结果如表4，测距结果如图12。

由表4可以看到，随着过渡电阻增大，对于单相接地、两相接地，故障集电线上零序电流主路径内外的零序电流都逐渐减小，但是主路径内部的零序电流仍远大于外部。层次一中由零序电流所得区域状态信息都与实际一致，故障区域均得到正确识别。这主要是因为过渡电阻影响的只是零序电流的绝对大小，而如6.1节所述层次一与零序电流绝对大小无关，所以层次一的可靠性得以保证。

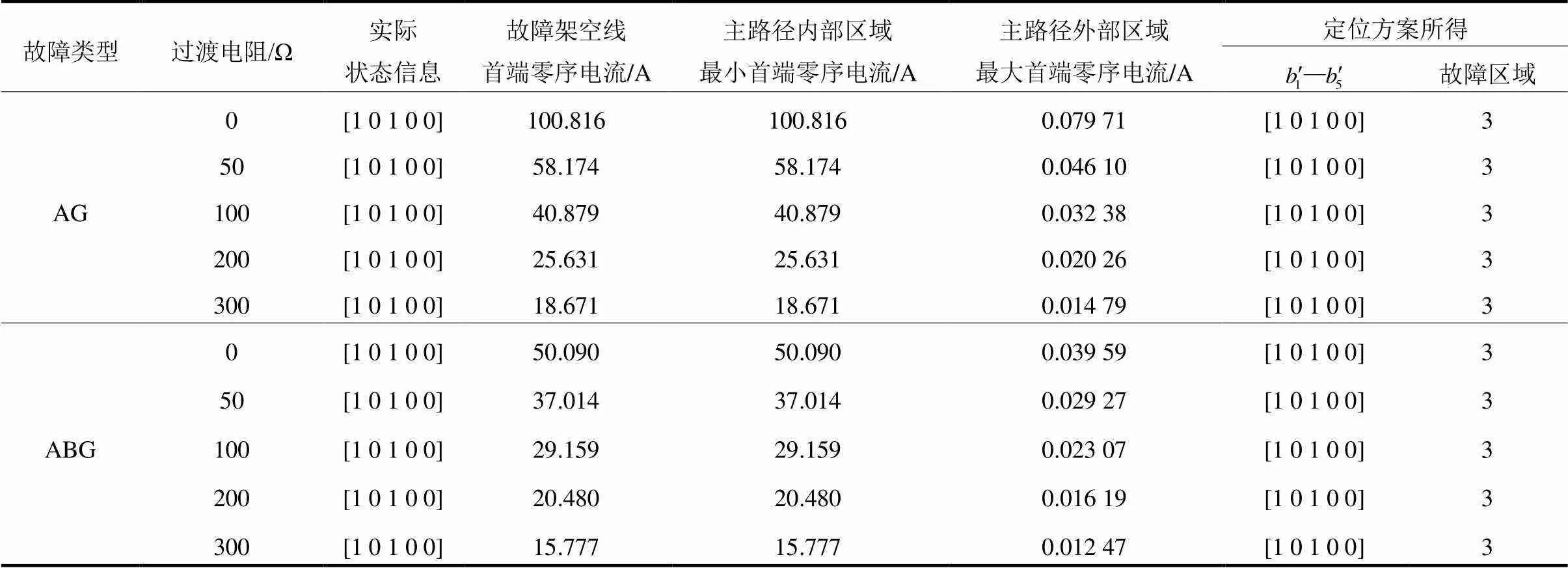
表4 不同大小过渡电阻下故障区域的识别

图12 不同大小过渡电阻下的测距误差

进一步，由于层次二的测距模型与过渡电阻无关，因此图12中层次二所得最大测距误差只有0.49%，验证了层次二的抗过渡电阻能力。以上表明，所提定位方案可以较好地克服过渡电阻的影响。

6.3 风机容量对定位方案的影响

6.1节设置了不同的故障位置，故障点至母线之间的风机数目也随故障位置的不同在0~5之间变化，因此本文定位方案消除风机影响的能力可以得到初步验证。为进一步验证上述性能，设置不同的风机容量进一步进行仿真。在集电线1的区域3上设置A相、AB相接地，故障点距区域3首端2026.22 m，过渡电阻为0 Ω。所得数据如表5和图13所示。

由表5可知，在不同风机容量下，层次一所得区域状态信息以及故障区域均正确；进一步，由图13中柱状图的高度变化趋势可以看出，层次二测距误差与风机容量之间没有明确的相关性，并且对于不同容量的风机，测距误差均较小，以上表明本文定位方案性能不被风机容量影响。因此，可以得出结论，所提定位方案可以有效消除风机影响，准确实现集电线故障定位。这一独特优势得益于本文对于风电场零序网络不含风机这一事实的利用。

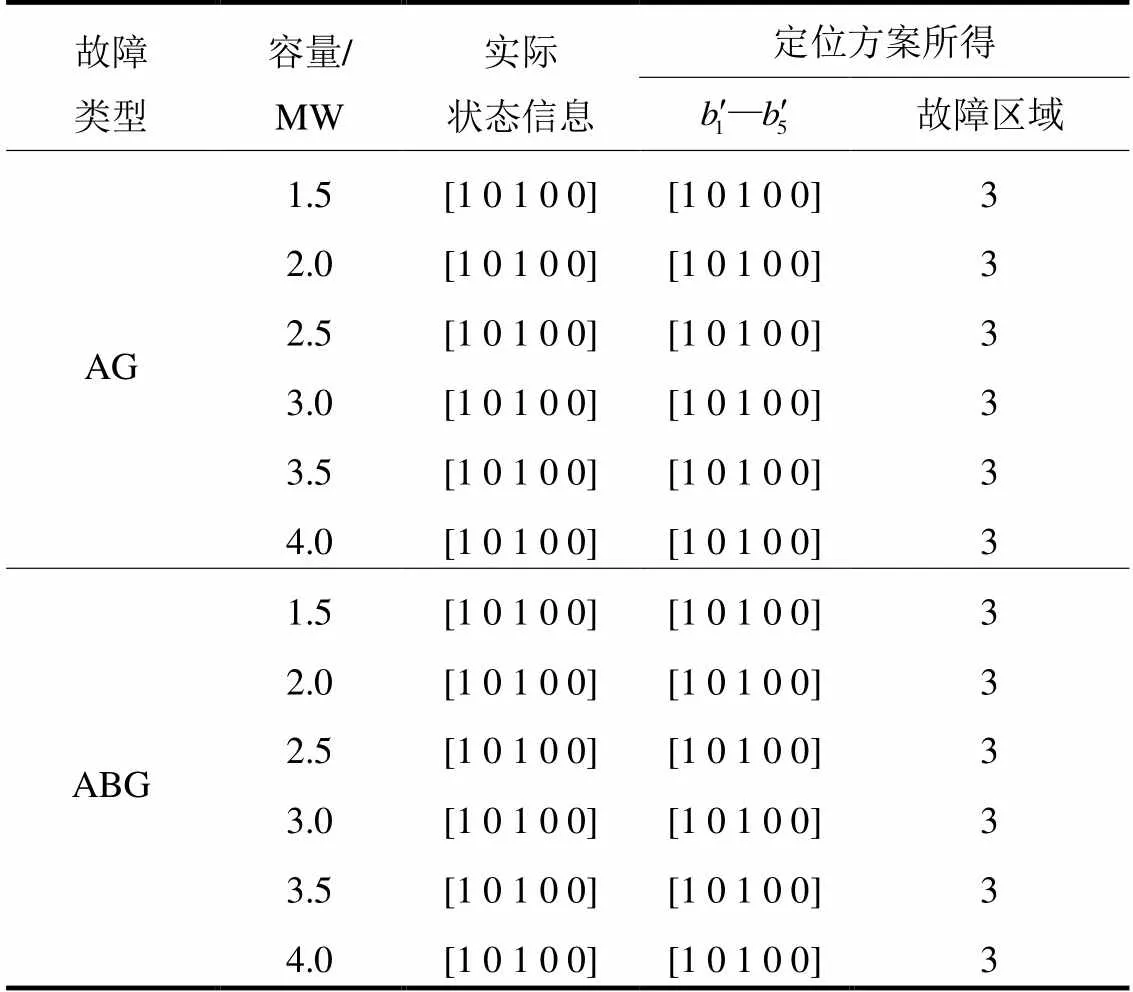
表5 不同风机容量下故障区域的识别

图13 不同风机容量下的测距误差

6.4 数据不同步对定位方案的影响

在集电线1的区域3设置A相接地故障，故障距区域3首端3310 m，过渡电阻为0 Ω，风机容量为2 MW。以区域3首端测点为参考，分别在其下游相邻区域(区域4、区域5)首端引入不同步角，以验证数据不同步对本文定位方案的影响。由于层次一基于电流有效值建立，而线路参数计算使用高精度同步相量测量装置，因此只需对层次二所得结果进行分析。相应结果如图14。图中横轴表示“区域4首端测点不同步角+区域5首端测点不同步角”。

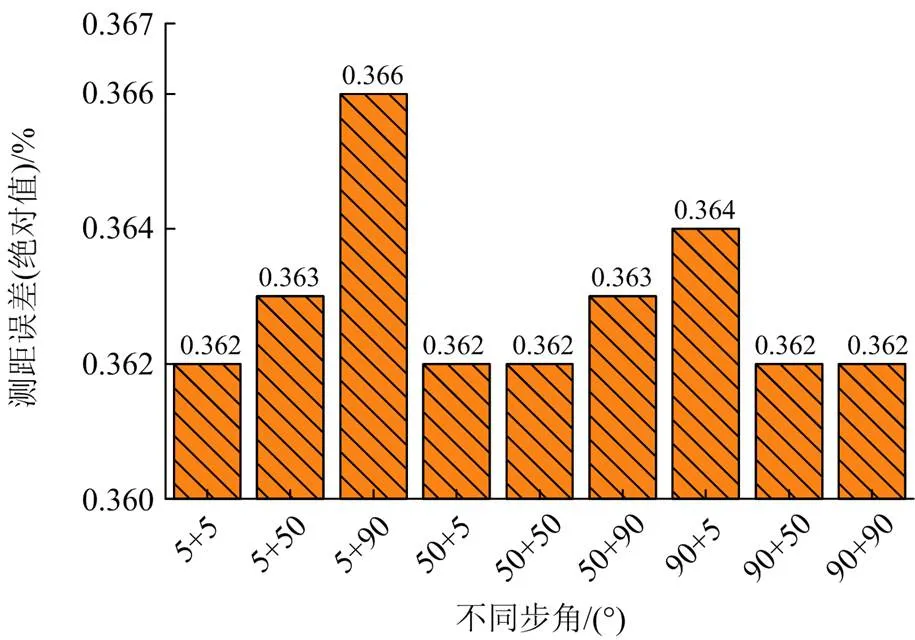
图14 数据不同步时的测距结果

由图14可知，当测点之间出现不同程度的数据不同步现象时，所提定位方案的测距误差变化很小，定位仍然较为准确。这是因为本文取模值建立测距模型，所以能够较好地消除测点间不同步角的影响。

6.5 线路参数变化对定位方案的影响

在集电线1的区域3上设置A相、AB相接地，故障点距区域3首端2026.22 m，过渡电阻为0 Ω，同时改变仿真模型线路参数模拟实际的参数变化。投入线路参数在线计算模块与定位方案相配合，所得参数计算及定位结果分别如表6和表7。

由表6可知，线路各参数的计算误差都较小，这表明本文线路参数在线计算模块具有较高准确性。由表7的定位结果对比可以看到，参数变化前后故障区域的识别均正确，这是因为参数变化与过渡电阻相同，只改变零序电流的绝对大小，所以不会对本文故障区域的识别造成影响；但是，在参数变化时仍然使用原始参数进行测距将带来相当大的测距误差，而采用计算所得参数进行测距时对应误差仅为0.82%、0.93%。以上结果表明，在线路参数在线计算模块的辅助下，本文定位方案能够有效克服线路参数变化的影响。

表6 架空线参数计算结果

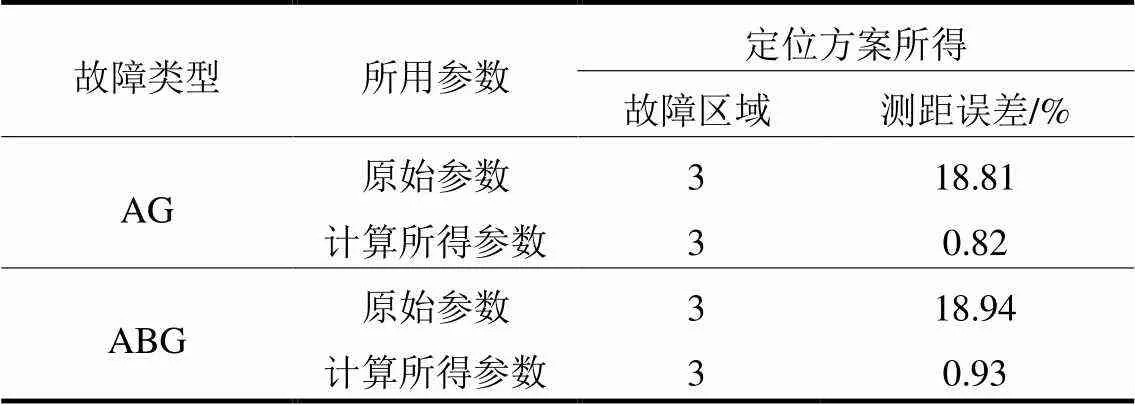
表7 不同参数下的定位结果

6.6 与现有方案的测距精度对比

本文和文献[15]所提集电线测距方案均为阻抗法测距，因此在此与文献[15]展开对比研究。以集电线1上的A相接地为例，在区域3距该区域首端700 m(故障点1)处以及区域4距该区域首端626.03 m (故障点2)处模拟故障，过渡电阻包括10 Ω、200 Ω。实施文献[15]所提方案时，默认故障区域已知，同时鉴于本文只研究纯阻性故障，文献[15]测距公式中电弧电压部分只计及电阻压降；按照本文假设进行风机故障电流近似计算后，将风机电流与架空线首端的A相电压、A相电流、零序电流代入测距公式计算故障距离。

由图15可知，当过渡电阻较小、故障点离架空线首端较近时，本文方案与对比方案都能够取得较为准确的测距结果，二者测距精度相当，但是图中其他情况下对比方案的误差较大，而本文方案对于不同故障场景都有着较高的测距精度，因此整体来看，本文可以更加有效地实现集电线故障测距。

图15 测距结果比较

7 结论

针对风电场集电线不对称接地故障的定位问题，本文提出了一种基于风电场零序分量的集电线故障定位新方案。所得结论如下：

1) 考虑风电场结构特点，基于零序分量构建定位方案，能够以较少测点完全消除风机影响，实现风机无关的故障定位，有效解决了电源数目多、故障特性复杂导致集电线定位困难的问题。

2) 所定义的无分支区域状态信息能够有效表征零序电流主流通路径，层次一通过状态信息优化匹配可以准确识别故障无分支区域，保证了定位方案对于含分支集电线的有效性。

3) 层次二基于零序阻抗构建，不需计及风机故障电流即可实现准确测距。同时，层次二采用优化思想求解故障测距模型，避免了解析法会出现的多解问题。

4) 层次一、层次二均不需严格的数据同步，并且定位性能不受故障位置、故障类型、过渡电阻的影响。同时，在线路参数在线计算方案的辅助下线路参数变化对测距的影响也得以克服。

风电场集电线故障定位目前仍是困扰风电运营商的难题，相对于现有方案，本文定位方案能够更好地兼顾其所面临的各关键问题，整体性能更优。在未来的研究工作中，将进一步减少测点数目，使方案经济性更好。

[1] ZHANG Ke, ZHU Yongli, LIU Xunchun. A fault locating method for multi-branch hybrid transmission lines in wind farm based on redundancy parameter estimation[J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(5): 1033-1043.

[2] 张科, 朱永利, 郑艳艳, 等. 风电场输电线路单相接地故障定位研究[J]. 太阳能学报, 2020, 41(5): 114-120.

ZHANG Ke, ZHU Yongli, ZHENG Yanyan, et al. Fault location of single-phase earth in transmission lines of wind farm[J]. Acta Energiae Solaris Sinica, 2020, 41(5): 114-120.

[3] 李练兵, 孙腾达, 曾四鸣, 等. 基于多端行波时差的配电网故障定位方法[J]. 电力系统保护与控制, 2022, 50(3): 140-147.

LI Lianbing, SUN Tengda, ZENG Siming, et al. Fault location method for distribution networks based on traveling wave time difference[J]. Power System Protection and Control, 2022, 50(3): 140-147.

[4] SHU Hongchun, LIU Xuhan, TIAN Xincui. Single-ended fault location for hybrid feeders based on characteristic distribution of traveling wave along a line[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 339-350.

[5] 李猛克, 王阳, 孙广, 等. 基于回归分析法的特高压直流接地极线路故障测距方法研究[J]. 电测与仪表, 2021, 58(9): 129-134.

LI Mengke, WANG Yang, SUN Guang, et al. Research on fault location method of UHVDC grounding pole line based on regression analysis[J]. Electrical Measurement & Instrumentation, 2021, 58(9): 129-134.

[6] 陶彩霞, 杜雪, 高锋阳, 等. 基于经验小波变换的混合输电线路单相接地故障测距[J]. 电力系统保护与控制, 2021, 49(10): 105-112.

TAO Caixia, DU Xue, GAO Fengyang, et al. Single-phase to ground fault location of hybrid transmission lines based on empirical wavelet transform[J]. Power System Protection and Control, 2021, 49(10): 105-112.

[7] 段宽, 樊艳芳, 王永进, 等. 基于波速补偿故障距离逐步逼真的直流线路行波测距方法[J]. 电力系统保护与控制, 2021, 49(11): 70-78.

DUAN Kuan, FAN Yanfang, WANG Yongjin, et al. A traveling wave ranging method for a DC line based on wave velocity compensation and fault distance approaching its real value gradually[J]. Power System Protection and Control, 2021, 49(11): 70-78.

[8] ROOSTAEE S, THOMAS M, MEHFUZ S. Experimental studies on impedance based fault location for long transmission lines[J]. Protection and Control of Modern Power Systems, 2017, 2(2): 169-177.

[9] GUILLEN D, SALAS C, SANCHEZ-GOMEZ L F, et al. Enhancement of dynamic phasor estimation-based fault location algorithms for AC transmission lines[J]. IET Generation Transmission & Distribution, 2020, 14(6): 1091-1103.

[10] JI Liang, TAO Xiaojie, FU Yang, et al. A new single ended fault location method for transmission line based on positive sequence superimposed network during auto-reclosing[J]. IEEE Transactions on Power Delivery, 2019, 34(3): 1019-1029.

[11] CHEN Jingwen, CHU Enliang, LI Yingchun, et al. Faulty feeder identification and fault area localization in resonant grounding system based on wavelet packet and Bayesian classifier[J]. Journal of Modern Power Systems and Clean Energy, 2020, 8(4): 760-767.

[12] 王浩, 杨东升, 周博文, 等. 基于并联卷积神经网络的多端直流输电线路故障诊断[J]. 电力系统自动化, 2020, 44(12): 84-92.

WANG Hao, YANG Dongsheng, ZHOU Bowen, et al. Fault diagnosis of multi-terminal HVDC transmission line based on parallel convolutional neural network[J]. Automation of Electric Power Systems, 2020, 44(12): 84-92.

[13] JAMALI S, BAHMANYAR A, RANJBAR S. Hybrid classifier for fault location in active distribution networks[J]. Protection and Control of Modern Power Systems, 2020, 5(17): 1-9.

[14] 张科, 孙立志, 朱永利, 等. 基于矢量偏离度的风电场集电线路故障定位方法[J]. 电力系统自动化, 2019, 43(10): 127-133.

ZHANG Ke, SUN Lizhi, ZHU Yongli, et al. Fault location method of wind farm collection line based on vector deviation degree[J]. Automation of Electric Power Systems, 2019, 43(10): 127-133.

[15] 王宾, 任萱. 中性点经小电阻接地风电场集电线路单相接地故障测距研究[J]. 中国电机工程学报, 2021, 41(6): 2136-2144.

WANG Bin, REN Xuan. Single-line-to-ground fault location in wind farm collection line with neutral point grounding with resistor[J]. Proceedings of the CSEE, 2021, 41(6): 2136-2144.

[16] 彭华, 朱永利, 袁胜辉. 风电场集电线路单相接地故障组合测距[J]. 仪器仪表学报, 2020, 41(9): 88-97.

PENG Hua, ZHU Yongli, YUAN Shenghui. Combined fault location for single-phase grounding of wind farm collection line[J]. Chinese Journal of Scientific Instrument, 2020, 41(9): 88-97.

[17] 郑艳艳, 朱永利, 刘童童, 等. 基于零序电流的风电场单相接地故障区段定位[J]. 系统仿真学报, 2019, 31(7): 1408-1415.

ZHENG Yanyan, ZHU Yongli, LIU Tongtong, et al. Single-phase grounding fault location in wind farm based on zero-sequence current[J]. Journal of System Simulation, 2019, 31(7): 1408-1415.

[18] 彭华, 朱永利. 基于apFFT频谱校正和XGBoost的风电场集电线路单相接地故障测距[J]. 电工技术学报, 2020, 35(23): 4931-4939.

PENG Hua, ZHU Yongli. Single phase grounding fault location for power lines of wind farm based on apFFT spectrum correction and XGBoost algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4931-4939.

[19]彭华, 王文超, 朱永利, 等. 基于LSTM神经网络的风电场集电线路单相接地智能测距[J]. 电力系统保护与控制, 2021, 49(16): 60-66.

PENG Hua, WANG Wenchao, ZHU Yongli, et al. An intelligent single-phase grounding fault location for a wind farm collection line based on an LSTM neural network[J]. Power System Protection and Control, 2021, 49(16): 60-66.

[20] 成和祥. 基于双馈风机短路特性的风电场集电线路继电保护整定方法研究[J]. 电力系统保护与控制, 2020, 48(16): 93-99.

CHENG Hexiang. Discussion on setting scheme of collecting line relay protection in wind farm based on a DFIG short-circuit characteristic[J]. Power System Protection and Control, 2020, 48(16): 93-99.

[21] HOERAUF R. Considerations in wind farm grounding designs[J]. IEEE Transactions on Industry Applications, 2014, 50(2): 1348-1355.

[22]曾德辉, 王钢, 李海锋, 等. 小电阻接地配电网多回线故障分析与自适应零序电流保护[J]. 电力自动化设备, 2019, 39(5): 45-52.

ZENG Dehui, WANG Gang, LI Haifeng, et al. Fault analysis of multi-feeder grounding fault and self-adaptive zero-sequence current protection scheme for low-resistance grounding distribution network[J]. Electric Power Automation Equipment, 2019, 39(5): 45-52.

[23] WANG Bin, NI Jiang, GENG Jianzhao, et al. Arc flash fault detection in wind farm collection feeders based on current waveform analysis[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(2): 211-219.

[24]袁冰, 王宾, 陆元园, 等. 风电场并网线路单相接地故障单端测距误差特性分析[J]. 电力系统保护与控制, 2016, 44(19): 63-69.

YUAN Bing, WANG Bin, LU Yuanyuan, et al. Error analysis of single-end fault location for single-line-to- ground fault in transmission line with wind farm connection[J]. Power System Protection and Control, 2016, 44(19): 63-69.

[25]王晨清, 宋国兵, 迟永宁, 等. 风电系统故障特征分析[J]. 电力系统自动化, 2015, 39(21): 52-58.

WANG Chenqing, SONG Guobing, CHI Yongning, et al. Fault characteristics analysis of wind power system[J]. Automation of Electric Power Systems, 2015, 39(21): 52-58.

[26] 卫志农, 何桦, 郑玉平. 配电网故障区间定位的高级遗传算法[J]. 中国电机工程学报, 2002, 22(4): 128-131.

WEI Zhinong, HE Hua, ZHENG Yuping. A refined genetic algorithm for the fault sections location[J]. Proceedings of the CSEE, 2002, 22(4): 128-131.

[27] 谢潇磊, 刘亚东, 孙鹏, 等. 新型配电网线路PMU装置的研制[J]. 电力系统自动化, 2016, 40(12): 15-20.

XIE Xiaolei, LIU Yadong, SUN Peng, et al. Development of novel PMU device for distribution network lines[J]. Automation of Electric Power Systems, 2016, 40(12): 15-20.

[28] 陈福锋, 赵谦, 兰金波, 等. 风电场汇流线路同步采样及差动保护[J]. 电力系统自动化, 2013, 37(14): 19-24.

CHEN Fufeng, ZHAO Qian, LAN Jinbo, et al. Synchronous sampling and differential protections of collector lines in wind farms[J]. Automation of Electric Power Systems, 2013, 37(14): 19-24.

Zero-sequence component-based fault localization for asymmetric phase-to-ground faults of collecting lines in wind farms

ZHU Yongli, DING Jia, PAN Xinpeng

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

A large number of power sources with complex fault characteristics are connected to the collecting line of wind farms so that fault localization for the line is difficult. This problem has been plaguing wind power operators. Therefore, this paper presents a zero-sequence component-based fault localization scheme for asymmetric phase-to-ground faults of collecting lines. Starting by defining the branch-free area and fully considering the special relationship between wind turbines (WTs) and zero-sequence components of wind farms, the WT-independent identification and fault distance calculation for the faulty branch-free area can be realized hierarchically. First, the concept of status information of branch-free areas is introduced to reflect the main flow path of zero-sequence current. Then the faulty branch-free area can be identified by using optimization to match the status information. Second, a fault distance calculation model of the faulty branch-free area is derived from zero-sequence impedance, and the solution problem of this model is transformed into an optimization problem to obtain the fault distance. The proposed localization scheme can completely eliminate the effect of WTs with only a few measuring points and effectively adapt to the collecting line with branches. In addition, strictly synchronous data is not necessary for this scheme and multiple solutions are avoided. Finally, in order to deal with line parameter variation, online calculation of line parameters is also designed. Simulation results verify that this localization scheme is accurate and not affected by WTs, fault locations, fault types, fault resistance and asynchronous data, and the overall performance is better than that of existing schemes. The effectiveness of online calculation of line parameters is also proved.

wind farm; collecting line; asymmetric phase-to-ground fault; fault localization; zero-sequence component

10.19783/j.cnki.pspc.220635

国家自然科学基金项目资助(51677072)

This work is supported by the National Natural Science Foundation of China (No. 51677072).

2022-05-01；

2022-08-25

朱永利(1963—)，男，博士，教授，研究方向为电力设备状态监测和分析、电力系统分析与控制等；E-mail: yonglipw@163.com

丁 嘉(1997—)，男，通信作者，博士研究生，研究方向为电力设备故障诊断；E-mail: jia_ding_0132@163.com

潘新朋(1997—)，男，硕士研究生，研究方向为电力线故障定位。E-mail: 1473893557@qq.com

(编辑 周金梅)