基于机器学习的短期电力负荷预测方法比较及改进研究
2023-02-22韩雅萱石梦舒黄元生刘敦楠段文军
韩雅萱,石梦舒,黄元生,刘敦楠,段文军
(1.华北电力大学经济与管理学院,北京 102206;2.华北电力大学(保定)经济与管理系,河北保定 071003;3. 北京信息科技大学经济管理学院,北京 100192)
1 研究背景
能源消费与经济发展密切相关,随着我国经济稳中向好增长,我国社会用电需求也将持续增速[1]。电力负荷预测是对未来电力负荷的时间分布和空间分布的预测,是能源系统高效、安全和稳定运行的前提和重要保障。中长期负荷预测是电力规划的基础,关系到我国未来能源发展战略的制定[2];短期的负荷预测是电力系统运行的基础,在电力调度工作中起到关键性作用[3]。调度机构通过短期电力负荷预测,可以高效定制发电计划,避免电力供应过剩或不足,在保障民生的同时降低调度成本,以节约能源,从而更好地保证电网安全稳定运行[4]。尹春杰等[5]、郭亦宗等[6]认为,售电公司、虚拟电厂、负荷聚合商等电力市场主体可以通过开展短期负荷预测负荷提高经营收益、发展新的商业模式。然而,由于短期负荷受自然情况、数据规模等影响,较为精准的预测具有一定的难度。
当前负荷预测主要有以下几种方法:基于历史数据的统计方法、基于数学思想的预测方法以及基于人工智能的机器学习方法[7]。相比于后期发展的机器学习算法,统计学的原理较为简单,理论也较为成熟。贾庆兰等[8]建立基于多变量时间序列的电力负荷预测模型,以获得更高可信度和精度的电力负荷预测结果。梁荣等[9]、Liu等[10]都以ARIMA模型为基础,分别结合深度学习和神经网络对短期电力负荷预测方法进行改进,前者提高了精度但未关注预测速度,后者以牺牲精度为代价取得了预测速度上的提高。李文静等[11]则是简化了LSTM 神经网络用于时间序列预测的门结构,以降低预测时间和复杂度。以上文献都采用了常用于负荷预测的典型统计方法,然而可以发现,传统的预测方法在预测精度上存在误差较大以及不稳定的缺点,此外,该类方法对于数据的要求更高,对于小样本以及不稳定的时间序列预测并不准确,因此部分学者开始研究机器学习方法,以打破负荷预测技术发展瓶颈。Guo等[12]、Fan等[13]认为,机器学习方法能够在一定程度上弥补传统方法的缺陷,为较为常用的随机森林(random forest, RF)、支持向量机(support vector machine, SVM)、 人 工 神 经 网 络(artificial neural network, ANN)等机器学习算法,具有较高的适应性和较好的拟合能力。
冯荣强等[14]运用长短期记忆神经网络(long short-term memory, LSTM)对于用户的家庭用电需求进行了预测, Megn等[15]采用灰色模型和无线基函数神经网络分别对上升趋势和周期波进行建模,证明了相比于传统方法,基于人工神经网络的改进算法在预测精度和预测风险方面表现更好。He等[16]为提升负荷预测的精确度,考虑了最小绝对收缩以及选择算子分位数回归神经网络(LASSO-QRNN),通过方法的组合,陈振宇等[17]、王飞等[18]提出了一种考虑负荷区间的概率密度预测方法,在一定程度上突破了负荷预测精度难以提高的限制。袁保平等[19]在差分进化算法和多层感知引擎的基础上,提出基于神经网络的短期电力负荷预测法和混沌智能特征选择。在算例分析中将本方法结果与其他短期负荷预测技术进行对比,证明将差分进化算法 (differential evaluation, DE)应用于人工神经网络能够更有效的提高预测的准确度。Tvrdík等[20]采用了3种类型的自适应差分进化算法(self-adaptive differential evaluation, SaDE)的非混合和混合变体解决4个实际基准问题,并将算法优缺点进行对比,为相关研究提供方向。
本文综合了长短期记忆算法和自适应差分进化算法的优点,在进行时间序列分析的基础上,利用自适应差分进化算法优化长短期记忆算法,提出了一种用于短期负荷预测的混合算法(SaDE-LSTM)。本文以我国2004—2018年社会月度用电量数据作为输入数据,首先对改进后的混合算法进行性能测试,其次对比相同场景下分别采用支持向量机、反向传播神经网络、自回归积分滑动平均等模型的预测结果,证明了SaDE-LSTM算法综合了长短期记忆算法在长序列预测准确率上表现优异和自适应差分进化算法搜索效率高的优点,能够快速寻优,提高收敛精度,从而提高预测精度。
2 模型相关算法原理
2.1 长短期记忆网络原理
长短期记忆网络是在循环神经网络(recurrent neural networks,RNN)是基础上发展而来,其结构如图1所示,是常用于预测的方法之一。Neeraj等[21]、Chahla等[22]基于该方法实现时间序列的分类及回归,进而对电力负荷进行预测。

图1 简单长短期记忆网络体系结构
为克服周期性神经网络的梯度消失和爆炸等缺陷,改进了长短期记忆网络的存储器单元结构[23],如图2所示。荆昱阳等[24]通过一个时间序列数据的拟合和预测问题,验证了改进的长短期记忆网络的单元结构在处理时间序列时具有良好的性能。查博等[25]则结合传统回归模型及神经网络模型,通过对比分析证明了长短期记忆网络在预测方面的优越性。

图2 长短期记忆记忆单元结构
长短期记忆网络结构的每个内存单元都包含3个重要组件:遗忘门f1、输入门it、输出门ot分别更新每个节点的遗忘、输入以及输出信息,从而实现信息传递和记忆长期状态。在信息传输过程中,长短期记忆网络通过当前输入信息、最后时刻的隐藏层状态信息以及最后时刻的单元状态和结构来处理单元状态信息,根据遗忘门和输入门的输出更新单元格状态优选信息。单元格状态更新是对该时刻单元格的历史状态信息和输入的新信息的同时更新。最后,隐藏层根据更新的单元格状态输出最终状态。长短期记忆网络的记忆单元更新流程如下。
(1)遗忘门ft的计算。遗忘门能够当前的输入以及历史的隐藏层输出,即控制t时刻输入值xt和t-1时刻隐藏层输出ht-1被遗忘的程度,进而筛选有效信息。遗忘门ft的计算公式是:

式(1)中,wf所代表的概念是在t时刻遗忘门ft的权值矩阵,bf所代表的概念是偏置量,σ一般为sigmond函数,起到门控作用。
(2)输入门it的计算。输出门控制t时刻输入值xt和t-1时刻隐藏层输出ht-1更新到记忆单元的程度大小。输入门it的计算公式是:

式(2)中:wi所代表的概念是t时刻输入门it的权值矩阵;bi所代表的概念是偏置量。
(3)记忆单元的候选状态ct的计算。ct由t时刻输入值xt和t-1时刻隐含层输出ht-1共同决定。记忆单元的候选状态ct的计算公式是:

式(3)中:wc所代表的概念是t时刻候选状态ct的权值矩阵;bc所代表的概念是偏置量。
(4)记忆单元状态值ct的更新计算。记忆单元状态值ct的更新计算公式为:

记忆单元ct通过输入门it和遗忘门ft调整自身状态ct-1和当前候选记忆状态值ct,从而更新记忆单元的状态。
(5)输出门ot的计算。输出门控制t时刻输入值xt和t-1时刻隐含层输出ht-1取决于t时刻记忆单元的程度大小。
输出门ot的计算公式为:

公式(5)中:wo所代表的概念是t时刻输出门ot的权值矩阵;bo所代表的概念是偏置量。
(6)隐藏层输出值ht计算。隐藏层输出值ht是由t时刻输出值ot与记忆单元状态值ct决定的,计算公式如下:

相比于循环神经网络在长序列预测的准确率低于短序列的情况,长短期记忆算法在长序列预测上也表现出较高的精度,长短期记忆网络能够对负荷数据之间的时间相关性进行充分利用,对时间序列进行分类、处理和预测,进而更加精确地进行负荷预测。
2.2 差分进化算法原理
区别于其他一些优化算法,差分进化算法的目标是全局优化,这使差分进化算法在电力系统频率预测这类对时间较高要求的领域有一定优势[26]。差分进化算法在优化过程中,从父代个体中随机挑选两个个体进而计算矢量差以生成差异矢量。通过选择新的个体以及对应差分向量来生成一个实验个体。在此基础上,父母和子代杂交产生新的后代个体。最后,通过选择符合条件的个体,将该个体信息保存到下一代,汪慎文等[27]对差分进化算法的原理进行了较为详细的介绍。标准的差分进化算法包括4个步骤,每个步骤的细节如下。
(1)初始化。在此步骤中,首先初始化参数,包括种群大小N,基因维度D,变异因子(也称为缩放因子)F,交叉率CR以及每个基因的取值范围然后,按照公式(7)随机初始化总体:

在公式 (5)中,i=1,2, ,N,j=1,2, ,D,rand 是均匀分布的随机数。

在公式(8)中,个体序列号r1,r2和r3是随机选择的并且彼此不同,并且与目标个体的数量i不同,因此种群大小N≥4。
(3)交叉。通过公式(9)的交叉操作产生了一个实验个体:

在公式(9)中 ,r(j)是一个服从[0,1]均匀分布的随机数,j表示基因的数量,交叉率CR通常由用户设置,范围为[0,1]。从公式(9)可以得知,得到的交叉率CR越小,全局的搜索效果越好。
(4)选择。DE采用“贪婪”的搜索策略,它将每个目标个体与其对应的个体竞争,比较适应性值。只有当实验个体的适应性值优于目标个体,时,实验个体才可以被选作后代个体。否则,目标个体将被选作后代。以最小化优化为例,选择操作如公式(10)所示,类似代价函数和误差预测函数,是一种适应性函数。
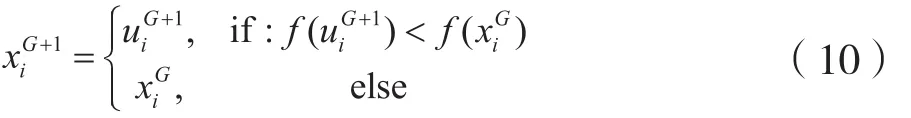
2.3 SaDE-LSTM原理
长短期记忆算法通过机器学习求出负荷和负荷的影响因素之间的非线性映射关系,但是其仅考虑了当前时刻的输入特征,忽略了连续负荷样本之间的序列的相关关系,缺乏了对历史信息的处理。为此,本文利用自适应差分进化算法改进长短期记忆算法。
自适应差分进化算法本身可塑性较强。吴文海等[28]将其与随机邻域策略和广义反向学习结合,进一步提高了算法寻优精度高和收敛速度。赵杨等[29]则将其与策略融合变异结合,提高了目标优化的搜索能力.随机自适应微分进化算法使用基于随机选择策略的突变运算,以较低的概率干扰自适应控制突变因子和交叉概率,以满足算法不同阶段的要求。自适应差分进化算法重点包含有自适应差分进化算法与适应差分进化算法(adaptive differential evaluation, ADE)。适应差分进化算法仅使用自适应突变因子。自适应差分进化算法在适应差分进化的基础上引入了适应性交叉因子,Qin等[30]对差分进化算法进行了深入解析。
(1)适应性突变因子。变异因子F决定了差分向量的尺度。得到的F越大,差分进化算法的搜索效率越低,导致全局搜索结果更差。但是,如果得到的F太小,种群多样性则会降低,并且算法会产生早敛。因此,本文提出了一种自适应突变因子,其基本原理公式(11)所示。
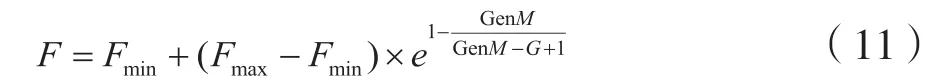
式(11)中,Fmin是最小变化因子,Fmax是最大变化因子, GenM是最大迭代次数,G是当前迭代次数。
(2)适应性交叉因子。初始时的大交叉因子能够确保变化在全局范围内发生,其后较小交叉率保证了局部收敛性。交叉因子的交叉速率随着迭代次数的增加发生动态变化。自适应交叉因子的设计如公式(12)所示:

式(12)中,CRmin所代表的概念是交叉参数的最小值,CRmin所代表的概念是交叉参数的最大值。
在进行时间序列预测的问题上,长短期记忆算法由于需要人工设定初始参数,例如隐含层层数、时滞、隐含层每层单元数等,人为设定难以实现最优解,且耗时费力。差分进化算法不依赖问题的特征信息,与其他优化算法相比,收敛速度快,全局优化能力强。在此基础上,自适应差分进化算法又能进一步解决差分进化算法在进化后期种群的多样性降低,以及容易出现过早收敛和精度不高的问题。因此,本文运用自适应差分进化算法确定最优的隐含层数以及每个隐含层的单元个数,运用自适应差分进化算法优化长短期记忆参数,提出SaDE-LSTM对短期负荷进行预测。
3 时间序列分析
3.1 序列的平稳性检验
本文选取我国31个省份2004年1月至2018年12月的月度全社会用电量数据作为原始数据[31],对数据进行处理。
如图2、图3所示,社会用电呈现清晰的逐年增长趋势和年周期规律,因此该数据的序列是非平稳的时间序列。

图3 2004至2018年我国31个省份用电负荷数据

图4 2004—2018年我国31个省份电力消费散点
在数据序列呈显著上升的情况下采用自相关图进行分析。如图5、图6所示,时间序列的自相关系数始终在x轴上方缓慢降低,存在拖尾特征,因此该序列为非平稳的。同时自相关系数长期位于零轴一侧,该序列为单调趋势序列。时间序列的自相关和偏自相关同时存在,进一步对序列进行差分运算。在5%的显著水平下,对时间序列平稳性进行检验,如表1所示,原序列在3种情况下都是非平稳序列,但其一阶差分序列和二阶差分序列都是稳态数组。

图5 2004—2018年我国31个省份电力消费自相关

图6 2004—2018年我国31个省份电力消费偏自相关

表1 2004—2018年我国31个省份电力消费时间序列平稳性检验
3.2 纯随机性检验
对数据进行延迟6阶和延迟12阶的白噪声检验,从表2可以看出,不同滞后期下P值均远小于0.05,因此该序列为非白噪声序列。

表2 2004—2018年我国31个省份电力消费滞后相关性Q检验
此外,由图7至图9可以看出该序列是具有随机性趋势的差分平稳序列,因此利用自回归综合移动平均模型拟合分析。

图7 我国31个省份电力消费一阶差分序列的时序

图8 2004—2018年我国31个省份电力消费一阶差分序列的自相关

图9 2004—2018年我国31个省份电力消费一阶差分序列的偏相关
4 模型检验及结果对比分析
本文以国研网数据库得到的月度负荷数据为基础,对提出的模型进行验证。其中,算例中将2004年1月至2018年2月月度用电量数据为训练集,以2018年3月至2018年12月的月度用电量数据作为测试集。
基于时间序列分析,运用自回归综合移动平均模型对算例数据进行预处理,如图10所示,用电数据模型呈现季节性和周期性特征。分别采用传统预测方法和本文提出的改进算法进行短期负荷预测。

图10 自回归积分滑动平均模型预处理的我国31个省份用电数据
4.1 支持向量机算法预测结果
支持向量机算法作为适用于小样本的预测方法之一,在负荷预测领域得到了广泛应用。如图11所示,采用支持向量机算法预测的负荷与实际数据存在较大的误差,并且存在变化趋势相反的情况。其中,最低误差9%,最高误差达27%。这表明,对于波动性和周期性较强的数据,支持向量机并未表现出良好的适应性和预测准确性。
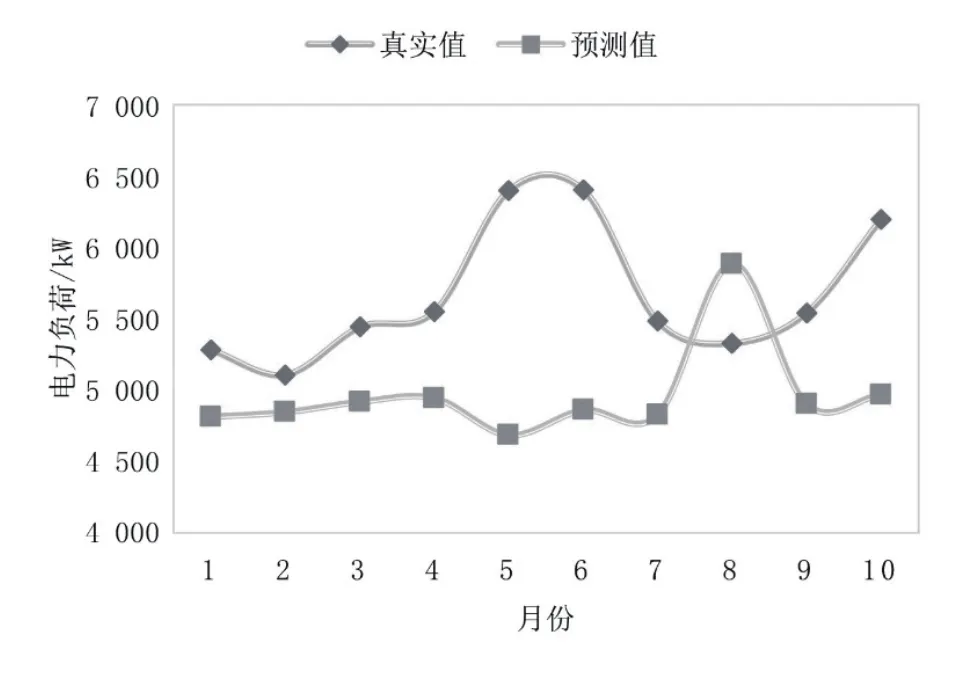
图11 2018年我国34个省级行政区电力消费的支持向量机算法预测结果和实际数据对比结果
4.2 长短期记忆算法预测结果
相比于支持向量机算法,长短期记忆算法更适用于具有波动性的时间序列预测。图12为采用长短期记忆算法预测的电力负荷趋势。参照图13显示,将预期结果与实际价值进行比较,我们可以看到明显的误差,标准误差是684.667 5,且无明显的一致性。

图12 采用长短期记忆算法的2004—2018年我国31个省份用电量预测结果

图13 2004—2018年我国31个省份用电预测值和实际值的误差
对原始数据进行更新,采用更新后的数据重新预测,运用长短期记忆算法预测得到的结果如图14所示,可以看出,标准误差为1 342.530 9,数据误差较大,准确率也并没有得到提高。因此,单独使用长短期记忆算法不适合本算例场景下的短期电力负荷预测。

图14 数据更新后2004—2018年我国31个省份用电预测值和实际值的误差
4.3 SaDE-LSTM算法预测结果
如图15所示,随数据量增大,SaDE-LSTM算法的训练结果与实际数据的重合度增加,偏离控制在0~10%以内,训练数据从整体略高于实际值到整体略低于实际值变化。在后续数据预测上数据重合度依然表现良好,整体趋势基本一致。在负荷低谷处的预测,误差基本为0,但是在几个负荷高峰仍然存在预测结果低于实际负荷的情况,最高误差为11%。

图15 采用SaDE-LSTM算法2004—2018年我国31个省份用电预测结果和实际数据对比
4.4 多种算法对比分析
图16展示了测试集2018年3月至2018年12月的实际电力负荷曲线与分别采用自回归综合移动平均模型,误差反向传播算法(back propagation,BP),利用自适应差分进化算法优化误差反向传播算法(SaDE-BP),支持向量机,利用自适应差分进化算法优化支持向量机算法(SaDE-SVM),长短期记忆算法,利用自适应差分进化算法优化长短期记忆算法(SaDE-LSTM)预测负荷曲线的贴合情况,其中采用误差反向传播算法,长短期记忆算法,SaDE-SVM,支持向量机算法的预测结果与实际情况相差很大,表明这些智能算法并不适用于该样本集的短期电力负荷预测情景。而自回归综合移动平均模型,SaDE-BP,SaDE-LSTM算法预测结果与实际趋势一致性较好,说明,这些方法对于具有明显时间序列趋势的数据具有更好的拟合效果,其中SaDE-LSTM算法预测曲线与实际曲线贴合度最高。

图16 2018年我国31个省份用电量的多种算法预测负荷与实际负荷对比
图17对多种算法的预测结果与实际结果偏离值进行了定量对比分析,通过对比误差反向传播算法,长短期记忆,SaDE-SVM,支持向量机等算法在短期电力负荷预测方面的预测效果,对不同算法的适用性进行了分析。可以看出,尽管误差反向传播算法、支持向量机等智能算法具有一定的优势,但是其在时间序列的预测中并未体现出优势。而单一的长短期记忆算法受参数影响较大,也存在表现不佳的情况。对图16中3种表现较好的算法的误差进行对比发现,SaDE-LSTM算法预测结果的每一个点的结果误差基本保持在0~0.5%之间,最大误差约1.6%。而自回归综合移动平均算法和SaDE-BP算法都有个别数据存在较大误差,通过图16可以判断自回归综合移动平均算法的偏离主要在5月、7月、8月,其最大误差为4.9%。SaDE-BP算法在7月之后的预测偏离较大,最大误差为10.4%。因此在短期电力负荷预测上SaDE-LSTM算法的准确率最高,表现最佳。
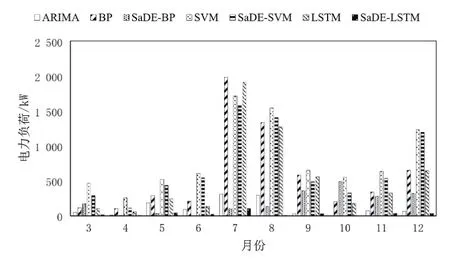
图17 2018年我国31个省份用电量的多种算法预测结果与实际结果偏离值比较
5 结论及展望
5.1 结论
本文提出了一种利用自适应差分进化算法优化长短期记忆算法的混合算法(SaDE-LSTM),在相同场景下,对比分析多种基于机器学习的负荷预测算法和所提出的改进算法的预测结果。在进行时间序列分析的基础上,经过数据训练后,自回归综合移动平均模型,SaDE-BP算法,SaDE-LSTM算法在月度短期负荷预测中具有更好表现。其中本文所提出的基于SaDE-LSTM的改进算法综合了长短期记忆算法和自适应差分进化算法的优点,弥补了长短期记忆算法搜索效率较低和自适应差分进化算法在长序列预测上准确性不足的缺点,预测短期负荷具有最高的精确的。因此,SaDE-LSTM算法能够快速寻优,提高收敛精度,从而提高预测精度,为电力系统的发展提供有力支撑。
5.2 展望
从电力系统角度看,电力调度机构需要不断改进短期负荷预测方法,进一步提高电力负荷预测的精度,减少预测的难度,从而提高发电设备的运转率和保证经济派遣的有效性,实现提高电力系统经济效益,保障电力系统安全有序运行的目的。
从电力市场角度看,在市场主体多元化发展的趋势下,基于用户需求,虚拟电厂、负荷聚合商等新型主体可以基于精确的短期负荷预测水平开展商业模式探索[32],一方面为其他主体提供负荷预测服务扩大收益来源,一方面能够利用负荷预测结果对聚合资源灵活调配,为电力系统提供平衡服务,最终达到利用市场化手段保障电力供需平衡的目标。
从电网角度看,预测中长期地区负荷结构变化,有助于配电网规划布局;准确预测短期负荷高峰[33],做好发、输、配、用各环节的调度,可以防止电力缺口出现,提高电网应对极端天气和特殊事件的能力,从而保障居民、工业用电,维护电网安全平稳运行。
