基于离散优化的飞行试验点优化设计方法

2023-02-22刘思余马明明

空气动力学学报 2023年1期

刘思余，梁言，马明明

(中国飞行试验研究院发动机所，西安 710089)

0 引言

飞行试验是航空科学技术探索和研究的有效手段，是新型飞机研制和鉴定的重要环节，是对航空新型号产品摸索和积累使用经验的必经之路[1]。由于飞行试验是一项风险大、复杂度高、成本大的项目，为了降低研制风险，加快研发进度，开展试验设计在飞行试验中的应用研究是关键措施之一。

以中心复合设计为代表的现代试验设计方法在航空航天领域有着大量的应用。美国NASA的Langley实验室[2]在1997年就开始将现代试验设计方法应用于风洞试验，国内的中国航天空气动力技术研究院[3]与中国空气动力研究与发展中心[4-6]分别针对亚声速、跨声速等高速风洞开展了一系列的试验设计应用研究。试验结果表明，采用试验设计方法可以有效地降低试验资源，提高试验效率。

Jon[7]将中心复合设计应用于航空发动机进口导向叶片共振频率试验，并将中心复合设计试验结果与全因子试验进行对比，认为通过试验设计方法可以得到更精确的物理模型；杨建华[8]采用均匀设计方法进行发动机性能试验设计，得到的特性规律模型误差不超过3%；范泽明[9]则采用正交设计方法进行航空发动机高空模拟试验，获得各试验因素对试验指标影响的显著性及交互作用；AARON[10-11]与黄陈生[12]等将中心复合设计应用于飞行试验中，得到了相关试验科目的规律特性模型。

上述研究均表明了试验设计在提升试验效率与试验结果上的有效性，但也反映了试验设计中存在的一些共性问题：1）试验设计过程存在对经验的依赖，具有一定的主观性，缺少试验设计的客观评价。试验设计的目的是得到一组试验点，然后通过试验点数据得到试验对象的特性规律模型；该特性规律模型的精度取决于试验设计好坏，因此特性规律模型的精度的可以作为试验设计的评价标准；2）试验对象本身存在使用限制，需要在限制范围内应用试验设计方法来安排试验[12]，但如何在限制条件内寻找一组试验点，使最终得到的特性规律模型的精度最高是试验设计需要考虑的问题。

综上所述，本文针对上述两个问题进行试验点优化设计方法研究，通过优化设计方法得到最优试验点组合集，使最终得到的被试对象规律特性模型精度最高。

1 试验对象规律模型构造方法

试验设计需要得到试验对象的特性规律模型，然后根据该模型进行试验设计。但在进行实际应用中，试验对象的特性规律模型可能存在缺失。因此，试验设计首先需要进行试验对象规律模型构造方法研究。

多项式模型具有结构简单、求解方便、计算效率高的特点，可以赋予模型物理意义。试验设计一般采用多项式模型来反映试验自变量与因变量之间的规律[2-8,10-15]；由于不同自变量对模型精度的影响不同，可以通过显著性检验量化自变量对模型影响性大小，剔除影响较小的自变量[16]，从而在保证模型精度的前提下简化模型。因此，本文通过多项式模型与显著性检验方法构造试验对象规律模型。

1.1 模型显著性检验方法

通过计算样本数据的总离差平方和SST、回归离差平方和SSM、剩余离差平方和SSL以及相应的自由度，然后再结合F检验就可以判断模型的显著性。具体计算公式如式（1～6）所示。其中，dfT是SST的自由度，dfM是SSM的自由度，dfL是SSL的自由度，下标i代表样本序号。F检验具体流程为：计算F=(SSM/dfM)/(SSL/dfL)，然后将其带入F(dfL，dfM)计算对应的概率PF。一般PF≤0.05是显著性可接受的标准。

1.2 自变量显著性检验方法

模型显著不能表明自变量的显著性。因此，需要进行偏回归系数分析以确定不同自变量的影响大小[16]，一般P≤0.05是显著性可接受的标准。具体方法如下：

1）计算信息矩阵A的逆矩阵C，其中，A=XTX，C=A-1；

2）计算第j个变量的偏回归平方和Uj，Uj=βj/cjj，cjj为C矩阵主对角线上的第j个元素；

3）计算第j个变量的F值以及对应的概率Pj，Fj=Uj/SSL，带入F(1，dfM)中计算Pj。

2 试验设计结果评估方法

试验设计的目的是获得试验对象的特性规律，但不同的试验点集合会得到不同的数学模型。因此，数学模型能否有效反映试验对象的特性规律是试验设计关注的重点。

3 限制条件下的试验设计方法

对于飞行试验而言，由于试验对象、试验平台存在使用限制，中心复合设计等试验设计方法得到的试验点不能很好地覆盖全包线；由于实际飞行中飞行条件存在波动，飞行员一般需要试验点的速度、高度取整，以便快速衡量试验点执行时的偏差。因此，飞行包线的不规则与试验点因变量取整是飞行试验设计的限制条件。

本文通过在飞行试验限制条件建立试验点库，组合不同试验点生成试验点组合集，然后以D-最优准则为评估方法，进行试验点优化设计，得到最有试验点组合集。

3.1 飞行试验点库建立方法

飞行试验中存在诸多限制，需要根据飞行试验限制条件建立飞行试验点库。具体流程为：1）确定飞行试验的试验因子，然后将试验因子的限制条件转换为试验点库的边界；2）选取合适的步长建立试验点库。

3.2 试验点组合集编码

本文的离散优化算法是在遗传算法的基础上改进的，替换了遗传算法中变量的编码过程，通过组合不同区域离散点序号得到试验点组合集编码，具体过程如图1所示：1）建立试验点库；2）划分试验点区域，并对区域内的试验点进行排序；3）依次在不同试验点区域中选取1个试验点，按照试验点区域顺序进行排列组合，完成编码过程。

图1 试验点组合编码过程Fig. 1 Encoding process of the test point combination

3.3 离散优化算子

生成新样本的优化算子分为选择、交叉、变异三个步骤[17]，具体过程如图2所示：1）选择过程：根据样本适应度选择父代，个体适应度越大，被选中的概率越大；母代为随机选择；2）交叉过程：根据父代/母代中的最大适应度判断是否进行交叉，适应度越大，交叉的概率越大；若满足交叉条件，则组合父代和母代的部分编码片段，得到新样本；3）变异过程：根据新样本的适应度判断是否进行变异。新样本适应度越大，变异概率越小。

图2 离散优化算子Fig. 2 Discrete optimization operator

3.4 试验优化设计

在试验点数量不变的条件下，离散优化能够得到该试验点数量下最优试验点组合集，但由于试验点数量的限制，该最优试验点组合集不一定满足最终的优化目标。因此，需要增加试验点的数量，然后在新试验点数量下重新进行离散优化，直到最优试验点分布满足优化目标，具体过程如图3所示：1）根据试验点数量n划分试验点区域；2）根据划分的试验点区域生成编码长度为n的初始样本；3）通过离散优化计算最优试验点组合；4）若该试验点分布达到优化目标，则优化完成；否则增加试验点数量，返回步骤1）重新计算。

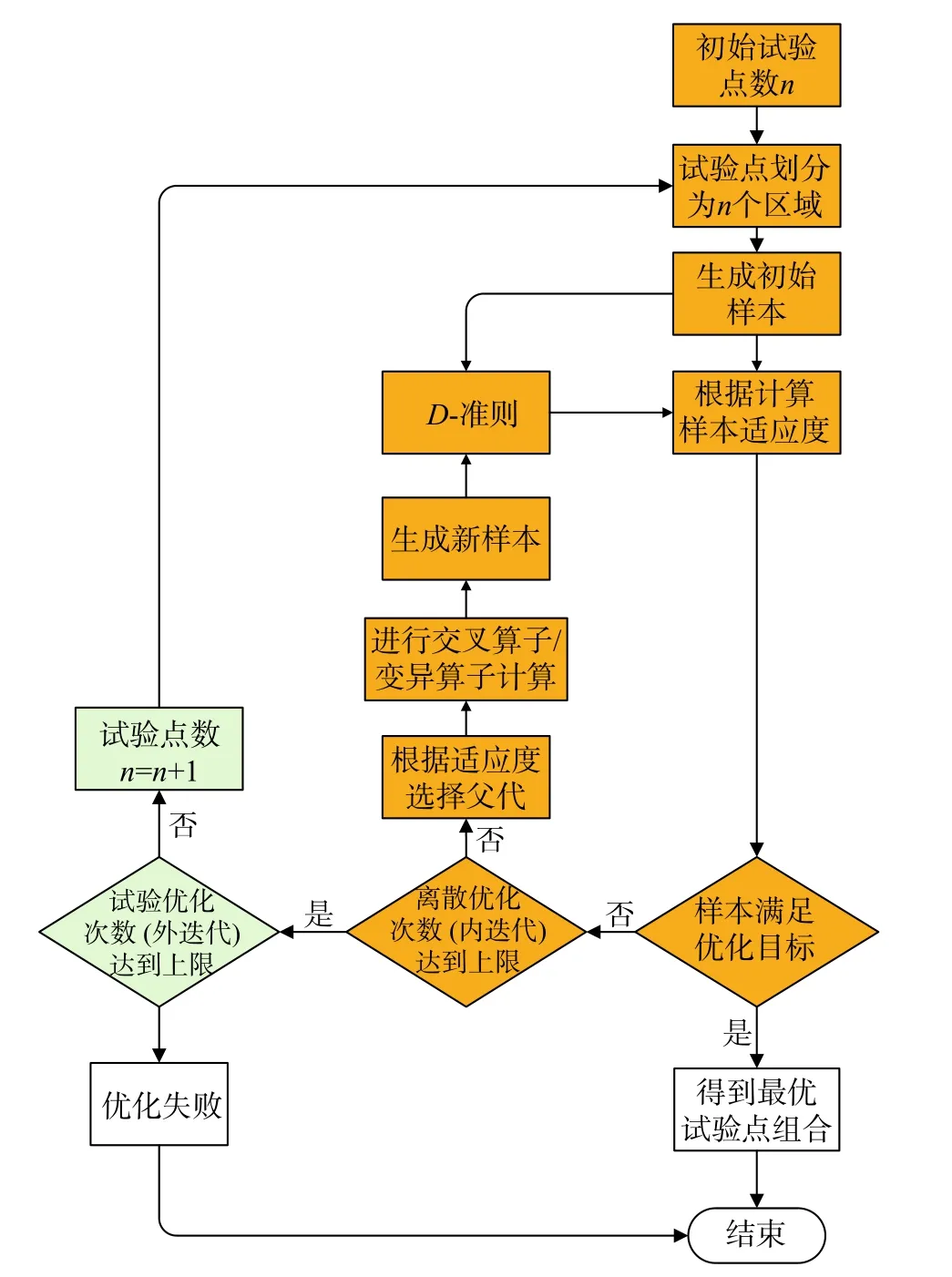
图3 试验点优化设计流程Fig. 3 Flow chat of the test design optimization process

4 算例应用

4.1 显著性检验案例应用

本文以某型发动机推力模型进行显著性检验案例应用。首先分析影响发动机推力的试验因子，然后再对发动机推力数据进行显著性检验，最终得到发动机推力模型。

航空发动机飞行试验中的试验因子分为外界因子与内部因子，外界因子包括飞行高度、飞行马赫数、大气温度、飞机过载、迎角、侧滑角等，内部因子包括发动机的供油量、尾喷口面积、高/低压压气机转速等。由于航空发动机飞行试验一般更为关注飞机平飞状态下的性能特性，飞机过载、迎角、侧滑角等机动状态参数可暂不考虑。因此，外界因子可只考虑飞行高度、飞行马赫数、大气温度。

航空发动机状态与低压压气机转速N1、高压压气机转速N2、高压压气机出口总压低压涡轮出口总温等多个参数有关，由于航空发动机自身存在特定的控制规律。因此，在外界环境一定的情况下，上述参数中的某一个参数确定，发动机状态也随之确定。

因此，对于某型发动机推力性能飞行试验而言，可以选定4个参数作为试验因子，分别是飞行高度H、飞行马赫数Ma、大气温度T、燃油流量W或高压压气机转速N2。一般选取发动机的典型状态进行试验，即固定发动机的N2，通过不同飞行条件下的发动机推力数据建立发动机推力性能规律模型。

假设发动机推力模型可以表现为如式（7）所示的3阶多项式，根据某型发动机额定状态的推力数据进行发动机推力模型显著性检验。该发动机与试验设计所针对的发动机为同一型号系列发动机，构建得到的推力模型在这一型号系列中具有通用性；显著性检验所需数据要较为全面，以保证显著性检验的有效性。根据显著性检验结果依次剔除最不符合要求的变量，直到所有变量的显著性均满足Pi≤0.05的要求。最终得到的发动机推力模型变量如表1所示。

表1 发动机推力模型显著性检验Table 1 Significance test of the engine thrust model

4.2 试验点优化设计案例应用

本文以某型发动机推力性能试验为对象，进行试验点优化设计。根据4.1节中的某型发动机推力模型，再结合各类试验因子中的限制条件，就可以完成试验点优化设计。

一般选取发动机的典型状态进行试验，即固定发动机的N2，然后在不同飞行条件下进行发动机推力性能试验。因此，试验点设计需要考虑的试验因子为飞行高度H、飞行马赫数Ma、大气温度T。对某机场四季大气温度进行统计，统计结果如图4所示，最终得到的某机场四季大气温度规律如图5所示。某机场大气温度限制可根据图5所示的规律得到；飞行高度H、飞行马赫数Ma根据飞行平台的包线进行约束。以上述限制条件作为约束建立试验点库，最终得到的试验点分布如图6所示。试验点库一共包含826个试验点。

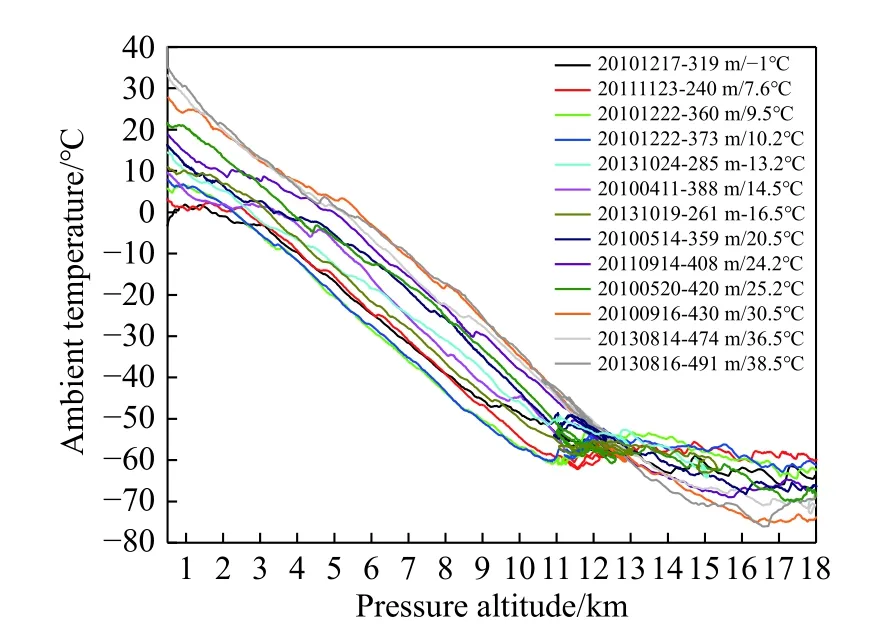
图4 某机场四季大气温度分布统计结果Fig. 4 Ambient temperature statistics of an airport

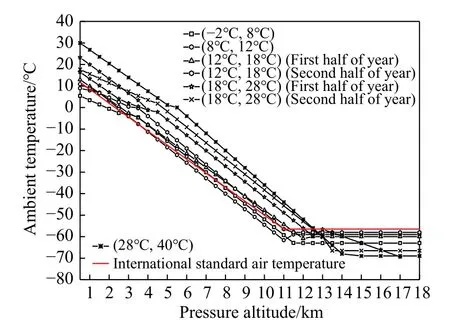
图5 某机场四季大气温度分布统计规律Fig. 5 Statistical law of the ambient temperature of an airport

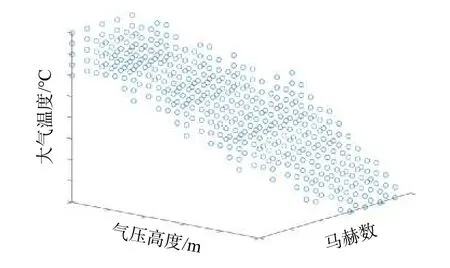
图6 试验点库Fig. 6 Test point dataset

发动机推力模型包含12个模型参数，至少需要12个试验点才能计算得到发动机推力模型。因此，试验点初始数量值为12；优化目标为lg(|M|/|M0|)＞4，即最优试验点组合集的信息矩阵行列式比初始试验点组合集提高4个数量级。给定试验点数量后，通过第3.4节中的试验优化计算方法进行计算。其中，离散优化次数上限值给定为500，优化样本总数为500。优化过程采用自适应遗传算法[18]进行计算，以提高算法的寻优能力与收敛速度。

若当前试验点数量下得到的最优试验点组合集不能满足优化目标，则增加1个试验点，然后再次进行优化计算。优化计算过程中需要注意的是：重新划分试验点区域时，需要保证不同试验点区域所包含的试验点数量基本一致，否则会引入误差。不同试验点数量的优化计算过程如图7所示，每次计算过程均收敛至当前试验点数量下的最优解。

图7 不同试验点数量下的优化计算过程Fig. 7 Calculation process for the optimization with different numbers of test points

当试验点数量增加11个试验点后，所得到的最优试验点组合集满足优化目标要求；最优试验点组合集优化过程如图8所示。得到的最优试验点组合集包含23个试验点，具体分布情况分别如图9、图10所示，所得试验点均在飞行包线与大气温度范围内。

图8 试验点组合集优化设计过程Fig. 8 Optimal design process for the test point combination

图9 试验点组合集优化结果（马赫-高度面）Fig. 9 Optimal result of the test point combination (Mach-altitude plane)

图10 试验点组合集优化结果（温度-高度面）Fig. 10 Optimal result of the test point combination(temperature-altitude plane)

采用某型发动机额定状态的推力性能计算程序计算得到试验点数据，该推力性能计算程序已通过某型飞行台数据进行校正，计算得到的数据具有可信度。根据试验点数据得到某型发动机额定状态的推力模型，并对推力模型误差进行统计，模型误差计算方法为：（试验点数据-模型数据）/试验点数据×100%，误差统计如图11所示，大部分模型数据误差绝对值小于0.5%，仅个别模型数据误差达到0.8%。

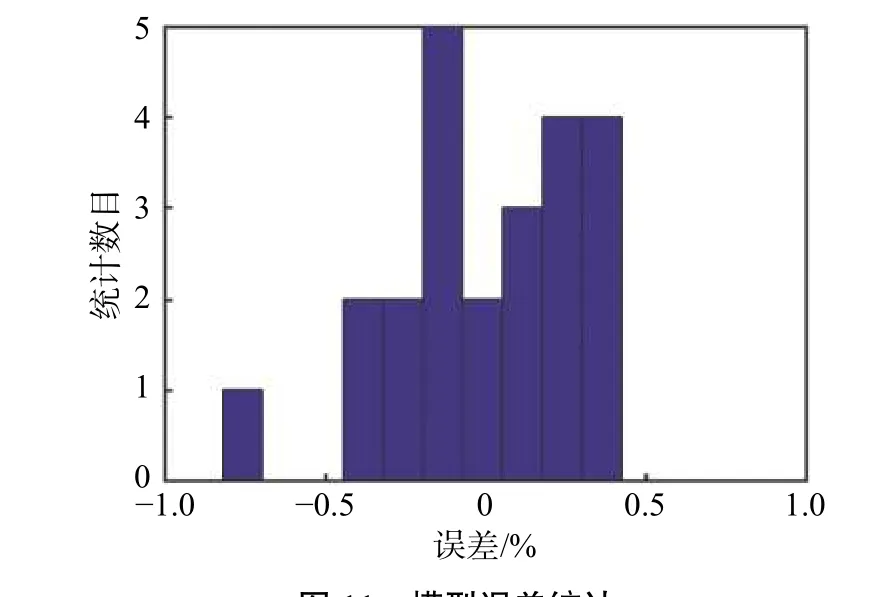
图11 模型误差统计Fig. 11 Statistical errors of the model

一般试验设计会设置验证点检验所得模型的精度[10-11]，本文设置6个验证点进行模型误差检验。6个验证点与试验设计结果中的试验点不重复，二者为相互独立关系；验证点分布于试验设计空间的不同边界处，具体分布如图12、图13所示。验证点误差如表2所示。通过最终试验点最优组合集得到的推力模型，其验证点误差绝对值均小于0.5%。因此，采用试验点优化设计方法得到的推力模型精度是远远满足工程与科研需求的。

图12 验证点分布图（马赫-高度面）Fig. 12 Verification point distribution (Mach-altitude plane)

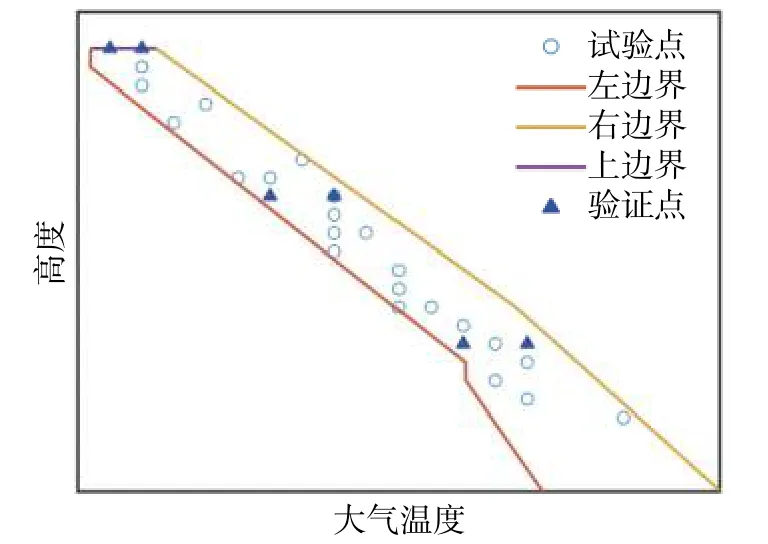
图13 验证点分布图（速度-温度面）Fig. 13 Verification point distribution(temperature-altitude plane)

表2 发动机推力模型验证点误差Table 2 Engine thrust model errors at verification points

为了对比本文提及的试验点优化方法的有效性，将初始试验点最优组合集与最终试验点最优组合集所得到的模型误差进行对比，对比结果如表2所示。在6个验证点中，初始试验点最优组合集由于试验点数量的限制，所得的推力模型最大误差绝对值达到2.45%，而最终试验点最优组合集得到的推力模型最大误差绝对值为0.45%。这表明了本文所用的试验点优化方法的有效性，同时也说明了试验点优化设计不仅与试验点的分布有关，也与试验点的数量有关。