数控卧式内腔加工专机联合仿真建模与分析

叶磊,成群林,雷怡凡,平昊,李凌霄,吕盾,周井文

1上海航天精密机械研究所;2西安交通大学机械制造系统工程国家重点实验室

1 引言

随着我国科学技术水平不断提高,在航天领域不断取得举世瞩目的成就,但同时呈现发射任务越来越重、发射间隔越来越短等特点,且航天产品有大量薄壁类舱体,舱体内腔存在许多窗口、网格和凸台等特征需要铣削加工。内腔加工专机是满足此类机加工要求的专用设备,已经得到广泛应用[1]。因此,为保证发射任务按时高质量完成,提高加工效率十分关键。

舱体类零件内腔加工路径为复杂空间轨迹,实际加工时动态误差对精度的影响远超过静态误差,因此,需要对内腔加工专机进行动态性能分析。一些学者通过机床动力学模型来研究机床的动态特性,张仁嘉等[2]建立了考虑间隙和滚珠丝杠间接触刚度的舵机动力学模型;鲁恒[3]采用集中参数模型建立了台式超精密机床动力学模型;白熹[4]基于分布质量法建立机床动力学模型;刘显军等[5]通过有限元方法分析多支承轴系的刚度;王小琼[6]通过有限元模型推导出四杆机构的动力学方程;Jiang T.等[7]建立了机床整机的有限元动力学模型;Pedrammehr S.等[8]使用解析法和有限元分析了机构的自由振动,并且计算了机构构型变化范围较大时的固有频率;位文明等[9]利用子结构法分析多轴承支承系统;白文吉[10]运用子结构法对xk2120型数控机床进行动力学建模;黄涛等[11]提出线性变参数动力学模型实验建模方法来构建高保真度滚珠丝杠传动系统动力学模型。

一些学者通过电机伺服控制建立机床伺服控制模型。王九高[12]研究了永磁同步电机的数学模型,并在Simulink软件中构建三闭环伺服控制系统仿真模型,通过仿真验证该方案的可行性。胡定—[13]研究了电机三闭环反馈控制技术,通过Simulink软件进行了仿真验证,并且完成伺服电机转矩控制实验台的搭建。

动力学模型或伺服控制模型只反映机构机械或者电气方面的特性,不足以反映机构的机电特性,为建立内腔加工专机高保真度仿真模型,需搭建机电耦合联合仿真模型。本文通过M序列与逆M序列产生激励G代码,通过指令位置数据与实际光栅位置数据建立各轴传递函数并进行验证,通过Adams与数值仿真软件建立机电耦合伺服控制模型,并进行联合仿真分析。仿真结果验证了所构建机电耦合伺服控制模型的有效性和可行性,为后续内腔加工专机的数字孪生研究奠定基础。

2 建立内腔加工专机联合仿真模型

内腔加工专机机电耦合联合仿真伺服控制模型建立流程如图1所示,分为创建激励G代码、建立传递函数、验证传递函数和建立联合仿真模型四个步骤。

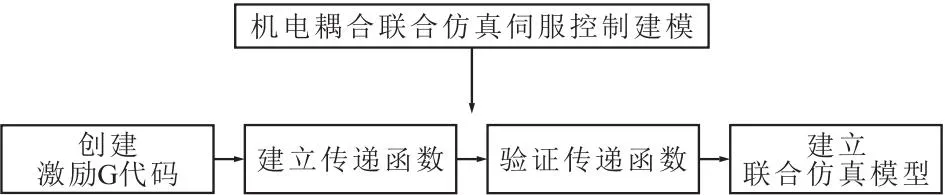
图1 联合仿真模型建立流程

2.1 生成激励G代码

选择合适的输入信号是获得理想传递函数的关键。目前,常用的激励信号有随机序列、伪随机序列和离散序列三类,这三类信号均有较好的辨识效果。由于工业设备难以完全按照随机序列和离散序列的变化规律进行相应运动,在工程上很难实现,因此,本文选择伪随机序列作为激励信号。

M序列及逆M序列是较为常见的伪随机序列。M序列是最长线性移位寄存器序列的简称,由多级移位寄存器或其延迟元件通过线性反馈产生最长的码序列。在二进制移位寄存器中,若n为移位寄存器的级数,则该寄存器共有2n个状态,除去全为0的状态外,还剩下2n-1个状态。因此,能产生的最大长度的码序列为2n-1,即一个n级线性反馈移位寄存器产生的最长周期为2n-1。

一般形式的线性反馈移位寄存器逻辑表达式为

(1)

式中,系数c1,c2,…,cn取值0或1;⊕为异或运算符。

将式(1)左边的an移至等式右边,并将an=c0an(c0=1)代入得到

(2)

定义与上式相对应的多项式

(3)

式中,x的幂次表示元素的相应位置。

式(3)为线性移位寄存器的特征多项式,特征多项式与输出序列的周期密切相关。n级线性反馈移位寄存器产生M序列的充要条件是移位寄存器的特征多项式F(x)为本原多项式。

设M(k)是周期为N、元素取值为0或1的M序列,S(k)是周期为2、元素取值为0或1的方波序列,将这两个序列按位进行异或运算,得到复合序列的周期为2N、元素取值为0或1的逆M序列,记为IM(k),计算式为

IM(k)=M(k)⊕S(k)

(4)

将上述逆M序列的逻辑值0或1分别变换为-1或1,此时逆M序列均值为0,且周期是M序列的两倍。此外,逆M序列具有逆重复性,前后两个半周期的变化情况相反。图2为N=40时的伪随机M序列和逆M序列。

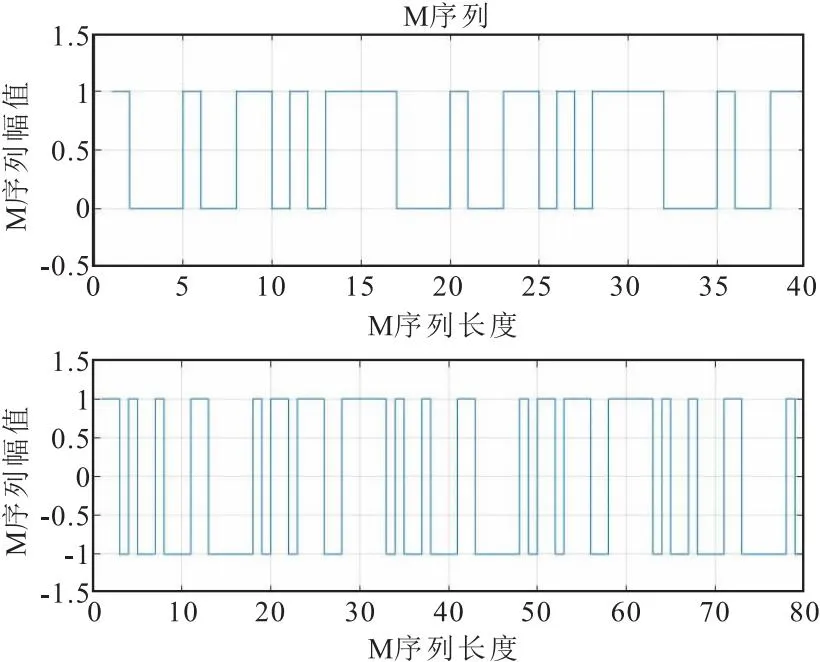
图2 M序列和逆M序列

为使内腔加工专机各运动轴在较大范围内运动,需改变逆M序列的幅值,使逆M序列幅值在较大范围内产生变化,并产生更好的激励效果。将逆M序列的幅值与一组随机序列进行运算,并考虑专机各运动轴限位,得到在专机各运动轴限位内变化的幅值。在数值仿真软件中实现这一运算过程,变化幅值后的逆M序列如图3所示。

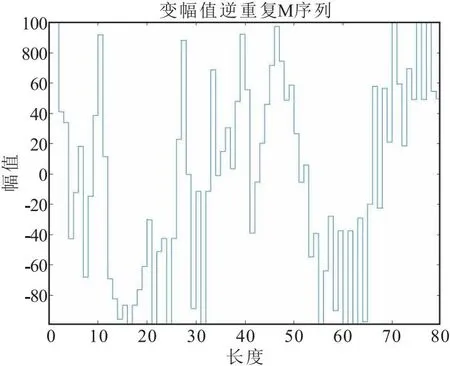
图3 变幅值的逆M序列

为了能激励专机各运动轴运动,需将变幅值的逆M序列转换成激励各运动轴运动的G代码,在数值仿真软件中将不断变化的逆M序列幅值转换成各运动轴坐标即可得到G代码。图4为生成的X轴激励G代码。

图4 X轴激励G代码

2.2 建立各运动轴传递函数

本文将各运动轴看作单输入单输出系统,如图5所示。输入为各轴指令位置,输出为各轴实际光栅位置。将前文生成的激励G代码输入专机数控系统中,使各运动轴产生相应激励运动。在该过程中,采集机床各运动轴指令位置和实际光栅位置数据,并建立各运动轴输入输出关系式。

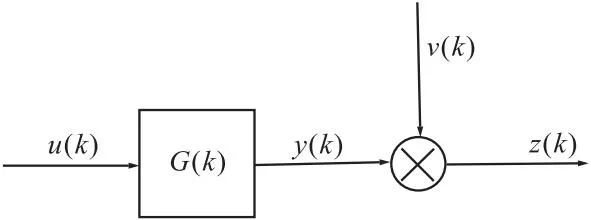
图5 单输入单输出系统结构

设在某采样时刻的输出为y(kT),输入为u(kT),为了书写方便,用y(k)表示y(kT),用u(k)表示u(kT)。在某采样时刻的输出值y(k)不但与该时刻的输入值u(k)及该时刻之前的输入值u(k-1),u(k-2),…,u(k-m)有关,且与该时刻以前的输出值y(k-1),y(k-2),…,y(k-m)有关,即n阶线性定常离散系统的差分方程[14]为

(5)

在零初始条件下,对式(5)进行Z变换可得

(6)

式中,y(z)为实际光栅位置;u(z)为指令位置;bi和aj分别为离散传递函数分子分母的系数;m和n分别为离散传递函数分子分母的阶数,系数和阶数均通过辨识来获取。对于实际的数控机床,根据物理可实现条件,应有n≥m。

在实际工程应用中,考虑到外界随机因素的干扰(见图5),得

v(k)=h(k)θ+v(k)

(7)

式中,v(k)为外界随机因素干扰。

θ和h(k)的表达式为

(8)

当有M组观测数据时,即k=1,2,…,M,将观测数据代入式(7)中,得矩阵形式为

ZM=HMθ+VM

(9)

式(9)中,ZM和HM的表达式为

(10)

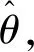
(11)

对式(11)进行求导,并令其等于0,即

(12)

有

(13)

(14)

将上文生成的各运动轴激励G代码输入专机数控系统中,使各运动轴产生激励运动。采集各运动轴的指令位置和实际光栅位置数据,如图6所示。

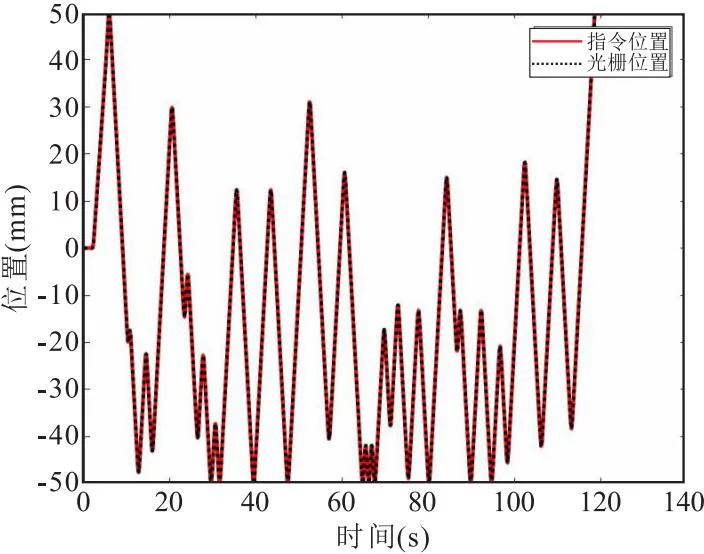
(a)X轴

采集各运动轴指令位置和实际光栅位置数据后,以指令位置为输入、实际光栅位置为输出,通过最小二乘法建立各运动轴输入输出之间的传递函数,如表1所示。

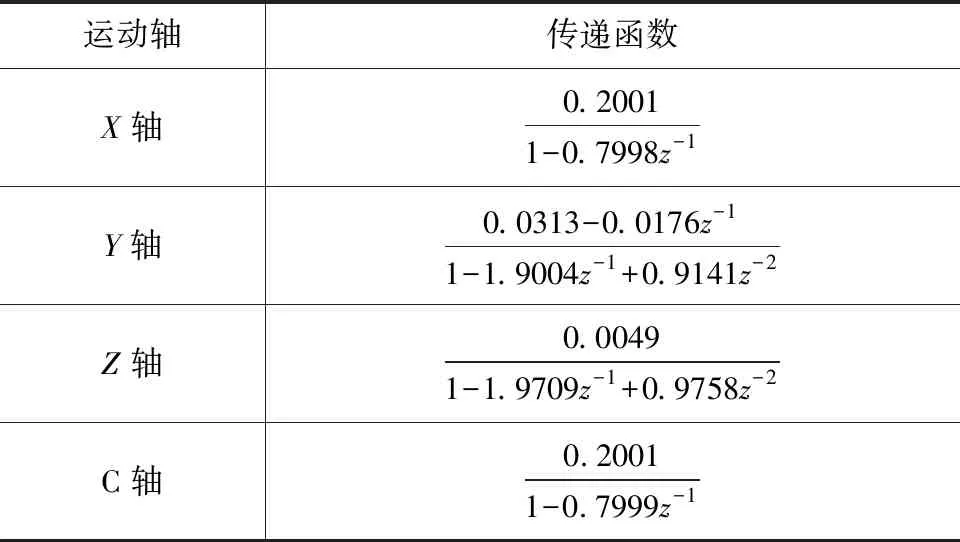
表1 各运动轴指令位置与实际光栅位置间的传递函数

2.3 验证传递函数

为验证各运动轴传递函数方程的准确性,将激励过程中的指令位置输入传递函数中,得到预测光栅位置,并与实际光栅位置进行对比。预测跟随误差,即指令位置与预测光栅位置的差值;实际跟随误差,即指令位置和实际光栅位置的差值;预测误差,即实际光栅位置和预测光栅位置的差值。通过以上步骤直观清晰地展示预测光栅位置和实际光栅位置的差值(见图7和图8)。

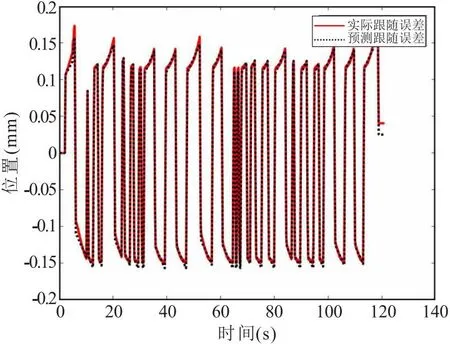
(a)X轴

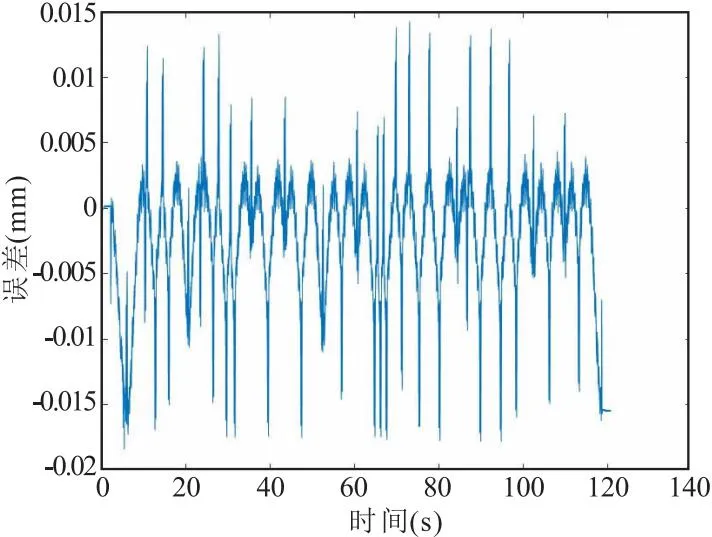
(a)X轴

从图7可以看出,X,Y,Z和C轴最大实际跟随误差分别为0.174mm,0.162mm,0.137mm和0.163°;最大预测跟随误差为0.157mm,0.170mm,0.115mm和0.163°;实际跟随误差与预测跟随误差变化趋势一致。从表2可以看出,X,Y,Z和C轴最大预测误差分别为0.018mm,0.022mm,0.007mm和0.019°。激励过程时,各运动轴振动会比正常加工时更加剧烈。内腔加工专机实际加工时,零件加工误差一般小于0.1mm,说明所建立传递函数满足精度要求。

表2 最大预测误差

2.4 建立联合仿真模型

利用前文所求并已验证的传递函数,通过Adams与数值仿真软件构建机电耦合伺服控制模型进行仿真,验证模型的正确性。在进行联合仿真前,先完成内腔加工专机Adams的材料属性定义、运动副设置、专机受力设置、设置状态变量并添加相应的驱动,完成Adams参数设置的内腔加工专机模型,如图9所示。

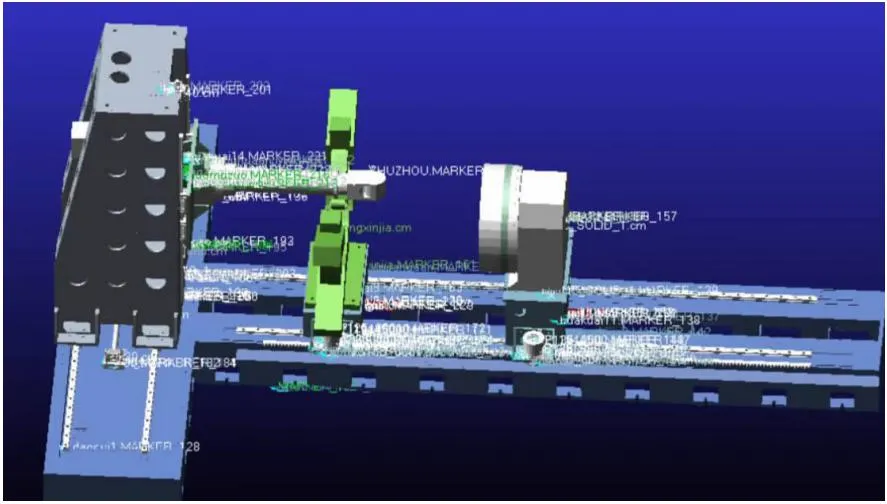
图9 内腔加工专机三维模型

将本文所需输入、输出参数通过Controls模块进行输出。完成Adams 参数设置后,需要在数值仿真软件调出Adams模块,如图10所示。

(a)XY控制模块

由于位置环在实际工程应用中通常只采用比例控制方式,本文在进行控制仿真时,仅仅调节kp比例系数,达不到误差小于0.1mm的控制精度。为实现高控制精度,在各轴控制环节中加入了位置前馈控制环节,设各轴传递函数为G(z),则前馈控制环节传递为1/G(z)。图11为XY轴联合仿真模型,图12为ZC轴联合仿真模型。

图11 XY轴联合仿真控制模型

图12 ZC轴联合仿真控制模型

2.5 联合仿真结果分析

运行联合仿真控制模型得到如图13所示各运动轴联合仿真模型输入与输出间误差。表3为X轴、Y轴、Z轴和C轴联合仿真模型输出值与实际指令输入值间的误差,分别为1.0×10-4mm,4.0×10-3mm,2.5×10-4mm和4.0×10-15°,满足实际工程应用中所需要的控制精度要求,证明了所建立的机电耦合联合仿真伺服控制模型的正确性。

表3 各运动轴联合仿真输入与输出间最大误差

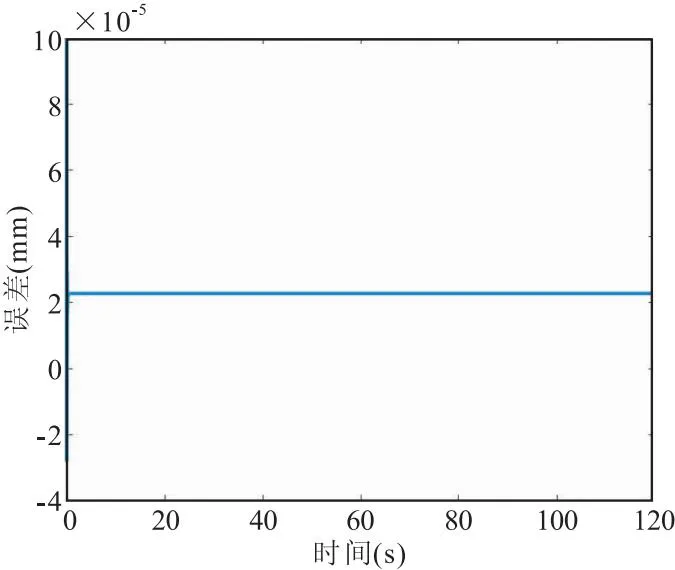
(a)X轴

3 结语

本文建立了各运动轴传递函数的方法,避免了传统动力学建模不够精准的问题,推导过程较简单。通过传递函数、Adams及数值仿真软件建立内腔加工专机机电耦合联合仿真伺服控制模型,解决机械机构与伺服控制系统不适配问题。联合仿真结果验证了所建立机电耦合伺服控制模型和位置前馈控制策略的正确性,对之后进行内腔加工机床数字孪生研究提供参考。该研究可为后续进行内腔加工专机数字孪生原型系统构建和智慧车间建设提供帮助。