基于用户价值和风险的云服务定价方法研究
2023-02-21叶春森周文强
叶春森, 周文强
安徽大学 商学院,合肥 230601
1 引 言
伴随数字经济的快速发展,云服务在世界范围内得到快速扩张[1],越来越多云服务应用被开发和使用[2]。据Gartner预测,2021年全球公有云服务终端用户支出将增长23.1%,总额达到3 323亿美元[3];2024年云服务将占全球企业IT消费市场的14.2%,相比2020年增长9.1%[4]。因此,云服务的价值已毋庸置疑。但是,随着云服务市场的快速增长,恶意攻击、网络故障、数据锁定等[5-6]风险事件频发。如最近日本政府使用的疫苗接种预约系统频现故障,根本原因就在于云计算服务商Salesforce公司所提供的云服务存在安全漏洞,因此用户对将云服务作为传统IT替代品的可行性仍存在疑虑,其信息感知逐渐从云服务的便利性和效率方面转移到安全可靠性上[7]。
目前,云服务定价研究的相关文献大多集中在经济学、计算机科学领域,其大致可以分为两类,一类文献从云服务用户角度展开研究:如Basu等[8]研究网络宽带服务质量对用户效用的影响,分析云服务用户选择不同购买方式的条件;Chen等[9]基于用户异质性建立一个双寡头模型,发现用户需求波动性影响用户选择,需求波动性较低的用户偏好基于预定方案,而需求波动性较高的用户偏好基于使用的方案;刘征驰等[10]引入用户群体异质性这一概念,发现用户适应度和交易成本直接影响云服务商利润以及用户对不同定价方式的选择。此外,更多学者分别从质量不确定性[11]、时间偏好[12]、转换成本[13]等角度刻画用户差异,研究用户偏好如何影响用户购买行为,并最终影响云服务提供商定价决策。
还有一类文献基于产品角度,其成果主要有:吴士亮等[14]建立旨在最大化垄断利润的非线性定价模型,研究计算资源容量对云服务定价决策的影响,得出计算资源充足时应采用按用量定价的方法,但没有考虑混合定价机制;鉴于此,Wu等[15]在固定定价以及按需定价基础上,综合考虑了混合定价模式,研究表明:当容量受到限制时,垄断云服务供应商的最佳策略是对异质需求用户使用混合定价策略;Huang等[16]认为云服务中断的存在可以对云服务进行质量区分,研究证明云供应商可以通过控制中断率改变用户购买行为以实现利润最大化。
云服务本质上是一种信息产品,非线性信息产品定价理论也是本文的理论基础之一。Sundararajan[17]考虑基于使用情况的定价方案管理成本,证明固定定价可以提高服务提供商的利润;Sridhar等[18]用频率和效用对不确定的用户使用需求进行建模,并表明当交易成本较低时,垄断者应该采用按用量定价;Fishburn等[19]通过对固定价格订阅和按使用付费的电子产品销售的研究,证明在市场竞争中,固定定价往往优于按用量定价;Cachon等[20]研究得出,当服务存在拥挤时,固定订价模式能让垄断服务供应商赚取更多利润。
综上可知,一方面,现有文献大多从单一定价机制或不同定价机制之间的比较等角度讨论云服务定价策略,但对混合定价机制关注较少;另一方面,对云服务定价的研究大多都囿于单一影响因素,较少考虑云服务风险对云服务定价的影响,同时缺乏多因素下的深入探讨。于是,本文通过引入风险因素并结合用户价值,构建基于用户价值和风险的效用函数,研究多重因素对不同定价机制选择与决策的影响。
2 模型描述

根据亚马逊、Google和阿里云的定价实践可知,固定定价和按用量定价是主流的两种定价机制。固定定价指CSP向所有用户实施统一固定价格T,用户付费后一定时间段内可无限量使用计算资源。根据定义可知,其交易成本为零。假定用户效用与使用数量、用户价值及风险有关,用户效用满足边际效用递减规律,当用户使用的云服务数量超过饱和阈值时,用户所获效用达到饱和上限。固定定价下用户使用量一般都达到饱和阈值,借鉴Sundararaja[17]和Chun[21]有关效用函数的假设,构建固定定价下的效用函数为
按用量定价指 CSP根据用户预期的计算资源使用量制定差异化价格表,用户从价格表中选择最优价格表单,将用户选择的预期资源使用量记为q(α,β),为此所支付的费用记为p(α,β)。对于按用量定价,CSP在监控用户单位时间使用的计算资源数量时会产生交易成本c。按用量定价下用户使用量一般小于等于饱和阈值,其效用函数为
3 基本模型
3.1 固定定价
首先考虑CSP提供单一固定定价机制的情形。用T表示CSP选择的固定价格;rs(α,β)为固定定价下的用户剩余,其等于用户获得效用与支付费用之差,即
rs(αU,βH)=0
(1)
由假设可知CSP的市场覆盖范围为[1-F(αU)] ×G(βH)。固定定价下CSP的利润为πs时,其优化决策问题为
定理1 在单一固定定价机制下,CSP的最优价格为2γ2,利润为2γ3/[e2δ(1+γ/δ)δ/γ+1],其随γ增加而增加,随δ减小而减小。
证明
(2)
由式(1)得
(3)
将式(3)代入式(2),则式(2)对α、β的一阶条件为
联立上述2式,可得均衡结果:
(4)
将式(4)代入式(2),可得:
对上分别求关于γ、δ的偏导,可得:

3.2 按用量定价
按用量定价机制下,CSP根据直接机制设计价格表,相应价格项记为(q(α,β),p(α,β))。用户从价格表中选择最优价格表单(q*(α,β),p*(α,β)),基于机制设计理论,其应满足以下两个约束条件:
[IC]U(q(α,β),α,β)-p(α,β)≥
U(q(x,y),x,y)-p(x,y)
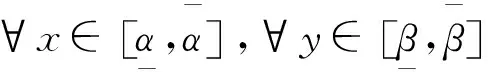
[IR]U(q(α,β),α,β)≥0,∀α,β
假设按用量定价下用户剩余为rd(α,β),则有
rd(α,β)=U(q(α,β),α,β)-p(α,β)=
(5)
类似于固定定价情形,设按用量定价机制下用户价值最低取值为αK,云服务风险的最高取值为βL,(αK,βL)满足:
rd(αK,βL)=0
(6)

因此,按用量定价下,当CSP的利润为πd时,其优化决策问题为
(7)
定理2 在单一按用量定价机制下,CSP提供的最优价格表单为
证明

q1(α,β)(α-β)-q(α,β)q1(α,β)-p1(α,β)=0
(8)
将式(5)对α求偏导,得:
rd1(α,β)=
q1(α,β)(α-β)-q(α,β)q1(α,β)-p1(α,β)+q(α,β)
将式(8)代入得:
rd1(α,β)=q(α,β)
rd12(α,β)=q2(α,β)
由原函数存在定理可知:
(9)
式(6)和式(9)联合得:
p*(α,β)=q*(α,β)(α-β)-
(10)
将式(10)代入式(7),可改写为
cq(x,β)]g(β)f(x)-

q*=α-β-c+γ
(11)
将式(11)代入式(10)解得:
如果CSP可以评估市场上的云服务风险(假设为βM),则上述表达式将变得相当简单。
定理3 如果CSP能够准确评估云服务风险,如为βM,则CSP最优价格表单为((α-βM-c-γ),(γ+c)×(α-βM-c-γ)),利润为γ2e-(βM+c+γ)/γ,其随γ递增。
证明
此时式(7)等价于
(12)
式(10)可改写为
p*(α,β)=q*(α,βM)(α-βM)-
(13)
将式(13)代入式(12),式(12)可改写为



q*=α-βM-c-γ
(14)
将式(14)代入式(13),得:
p*(α,βM)=(γ+c)(α-βM-c-γ)
(15)

q*=αK-βM-c-γ=0
αK=βM+c+γ
(16)
将式(14) 、式(15)和式(16)代入式(12)得:
(17)

3.3 混合定价
本文所讨论的混合定价机制指CSP同时提供固定定价和按用量定价两种定价机制。假设CSP仍沿用上文的按用量定价合同,当用户以固定定价机制购买的剩余大于按用量定价机制购买的剩余时,用户选择固定定价机制,反之,用户会选择按用量定价机制。
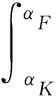
对固定定价和按用量定价两种定价机制之间无差异的客户类型记为αF,若α>αF,用户选择以固定定价机制购买云服务;若α<αF,用户选择按用量定价机制购买云服务。将混合定价机制下新的固定价格记作TF,则有:
V(αF,βM)-U(q*(αF,βM),αF,βM)+p*(αF,βM)=TF
(18)

αF>αK>0
(19)
CSP的综合利润由两部分组成,其定价决策问题可表示如下:

定理4 风险βM一定时,混合定价机制下,CSP按用量定价下的最优价格表单为((α-βM-c-γ),(γ+c)(α-βM-c-γ)),固定定价下的最优价格为γ(γ+c)2/2c。此时CSP的利润为γce-βM/γ-(γ+c)2/2γc+γ2e-(βM+c+γ)/γ。
证明
由式(18)可得:
(20)
由式(16)和式(20)得:
(21)
式(21)对αF的一阶条件为
解得:
(22)
式(22)代入式(19)得:
0 (23) 式(22)代入式(20)得: (24) 将式(22)代入式(21)得: (25) 同时可以发现,混合定价机制下,CSP通过制定更高的固定价格TF以及差异化的价格表攫取了更多的用户剩余;相较于单一按用量定价机制,混合定价机制在一定程度上节省了交易成本,提升了CSP的收益,由此可知,这种定价机制对CSP具有一定优势。 综上分析可知,CSP的3种定价机制在不同方面各有优势。本节通过这3种定价机制下的利润比较来讨论CSP采纳不同机制的条件。通过对不同机制的对比,得到定理5。 定理5 CSP应根据不同市场特征选择最适宜的定价机制以获得最大利润。当0<γ≤c,即市场上高价值用户较少时,CSP应提供单一固定定价机制;而当0 证明 固定定价下云服务供应商利润最大化的目标函数为 (26) βM一定时,用户剩余满足: rs(αU,βM)=0 (27) 联立式(26)和式(27)解得: αU=2γ+βM (28) T*=2γ2 (29) 将式(28)、式(29)代入式(26)得: (30) 由式(17)、式(25)、式(30)可知: 当0<γ≤c时,混合定价条件不满足,此时只考虑单一定价机制。 由于πs(α)>πd(α),此时CSP会选择单一固定定价机制,从而获得更大收益。 当0 由此可知混合定价机制优于单一按用量定价机制,此时再来判断πs+d(α)和πs(α)的大小。 图1 h(t)随t的变化趋势图Fig.1 Change in h(t) with t 由图1可知:当0 定理5表明:风险一定,当市场平均用户价值较低时(0<γ≤c),CSP的最优选择是只提供固定定价机制,此时市场上只有少数高价值用户,大多数都为低价值用户,这是云服务产品早期市场的特征。实施这种定价机制可以保证CSP在市场发展初期阶段获得稳定利润,从而在市场上站稳脚跟。另一方面,固定定价机制能让用户对产品产生黏性,使得高价值用户逐渐增多,从而会有更多用户愿意采纳云服务并倾向大规模使用。 当市场平均用户价值较高(0 从另一个角度理解,给定用户价值α,CSP也可以通过判别风险β的大小进行最优定价机制决策。讨论逻辑同上,不再赘述。 本节探讨用户在存在按用量定价机制的情况下采用固定定价机制的条件。首先建立一些与按用量定价机制相关的初步结果。设F(q(α,β),α,β)为选择按用量定价机制下的用户剩余,则有: F(q(α,β),α,β)=U(q(α,β),α,β)-p(α,β) 满足: F2(q(α,β),α,β)=q>0 F3(q(α,β),α,β)=-q<0 说明用户剩余随α增加而增加,随β增加而减少,揭示了对于β低而α高的用户选择按用量定价机制的动机。 当CSP另外提供固定定价机制时,用户只有在下列情况下才会选择固定定价机制: 设X(q(α,β),α,β)为用户选择盈余,将其定义为X(q(α,β),α,β)=V(α,β)-U(q(α,β),α,β)+p(α,β),当X(q(α,β),α,β)≥T时,用户选择固定定价机制;当X(q(α,β),α,β) 分别用βH、βL表示高风险环境和低风险环境两种情境,并假设在高、低风险环境下,CSP所提供的两种定价机制价格不变。 用αu|β=βH、αu|β=βL分别表示在高、低风险下,用户选择购买云服务用户价值的最低阈值,定义如下: ∀α<αu|β=βL,q(α,βL)=0 ∀α<αu|β=βH,q(α,βH)=0 用αs|β=βH和αs|β=βL分别表示在高、低风险环境下,用户从按用量定价机制转向固定定价机制付费的用户价值最低阈值,定义如下: αs|β=βL=Min{X(q(αs|β=βL,βL),αs|β=βL,βL)=T} αs|β=βH=Min{X(q(αs|β=βH,βH),αs|β=βH,βH)=T} 由αs|β=βL的定义可知,当α=αs|β=βL时,X(q(α,βL),α,βL)恰好等于T;且由X2(q(α,β),α,β)>0可得,当α>αs|β=βL时,X(q(α,βL),α,βL)>T,用户会选择固定定价机制。αs|β=βH同理。 定理6 在混合定价机制下,受用户价值以及风险因素的影响,用户选择将遵循以下条件: ①αs|β=βH>αs|β=βL; ②αu|β=βH>αu|β=βL。 证明 ① 由αs|β=βH和αs|β=βL的定义可得: αs|β=βL= 当在高、低风险下,用户消耗相同的资源量q时,有 由βH>βL,得αs|β=βH>αs|β=βL。 ② 假设αu|β=βH<αu|β=βL,根据αu|β=βL的定义可得: U(q(αu|β=βL,βL),αu|β=βL,βL)-p(αu|β=βL,βL)=0 由βH>βL,有 U(q(αu|β=βL,βL),αu|β=βL,βL)≥ 代入得: U(q(αu|β=βL,βL),αu|β=βL,βH)-p(αu|β=βL,βH)≤0 由上文知rd1(α,β)=q(α,β)>0,净效用随α递增,这与αu|β=βH的定义相矛盾,故αu|β=βH>αu|β=βL。 条件①表明:在高风险环境下,只有高价值用户会从按用量定价转向以固定定价机制购买云服务。这是预期的结果,因为固定定价机制是独立于使用情况的购买方式。高风险环境使得用户在使用时承担很大的风险,用户只会使用云计算处理必要的任务,因此一般不会选择固定定价,从而减少未使用计算资源的损失,除非用户从云服务中能获取非常高的价值。 条件②指出:在高风险下,高价值用户才会采用云计算服务。因为非高风险降低了用户效用,以至用户的净效用基本上小于零,因此只有较高价值的用户才会采用。 推论1 相对于低风险环境,高风险环境下不购买云服务的用户数量增加,且购买者更倾向于按用量定价机制。 证明高、低风险下愿意购买云服务的用户数量分别为1-F(αu|β=βH),1-F(αu|β=βL);偏好以固定定价购买云服务的用户数量分别为1-F(αs|β=βH),1-F(αs|β=βL);偏好按用量定价购买云服务的用户数量分别为F(αs|β=βH)-F(αu|β=βH),F(αs|β=βL)-F(αu|β=βL)。 由αu|β=βH>αu|β=βL,αs|β=βH>αs|β=βL得: 则有: 推论1表明:相对于低风险,在高风险下愿意以固定定价机制购买云服务的用户比例减少,且购买云服务的用户群体也会减少。如图2所示,伴随云服务风险升高,云服务市场规模会逐渐缩小,且此时市场上有一部分用户会从以固定定价机制购买云服务转向以按用量定价机制购买。 图2 混合定价下风险对用户选择的影响Fig.2 The impact of risk on user choice under the mixed pricing mechanism 本文定义社会福利为CSP利润和用户剩余之和,记为W,根据定义W=π+r,固定定价下用户剩余为 将式(28)、式(29)代入上式,解得: 按用量定价下用户剩余为 将式(14)、式(15)和式(16)代入上式可得: 混合定价下用户剩余由两部分组成: 将式(16)、式(22)和式(24)代入上式可得: 同理,可得: 首先比较Ws+d和Wd的大小: 由此可知,混合定价机制下的社会福利大于单一按用量定价机制。然后再比较Ws+d和Ws的大小: 图3 k(t)随t的变化趋势图Fig.3 Change in k(t) with t 由图3可知,只有当γ远大于c时,k(t)>0,即混合定价机制的社会福利大于单一固定定价机制。这说明单位交易成本的高低是按用量定价机制能否创造价值的关键。 本文从用户价值和风险视角研究固定定价、按用量定价以及混合定价机制的交互交纳机理,探究不同定价机制下的CSP利润、用户剩余以及社会福利的性质和差异,为解释和预测云服务市场的定价决策提供相关支持。研究表明:CSP在用户价值较低的市场应提供单一固定定价机制,而在用户价值较高的市场,应提供混合定价机制;随着云服务风险增大,会有一部分用户从固定定价机制转向按用量定价机制购买云服务,且购买云服务的用户群体会逐渐缩小;混合定价机制在吸引新用户、扩大市场占有率方面比单一定价机制更有效;单位交易成本的高低是按用量定价机制能否创造价值的关键,在混合定价机制下,降低交易成本有助于提高CSP利润和社会福利。 鉴于风险与云服务市场发展的关系,本文的研究结论在定价机制设计与优化方面有3个方面的管理启示:首先,CSP在设计价格列表时,除考虑部署成本差异之外,也要要考虑不同风险环境下的用户效用变化;其次,云服务风险对不同定价机制下用户量份额的影响机制研究,为CSP基于风险对用户进行细分提供新的视角与方法;最后,在云服务市场初期,低价值的用户集中度高,采用者比例小,较低的固定价格是一个很好的渗透策略,随着市场的成熟和用户价值分布的均衡,CSP应该提高固定价格,并逐步培育按用量定价用户群体,以获得更大的整体利润。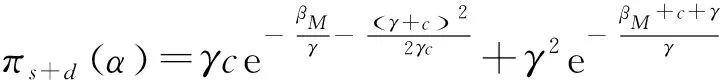
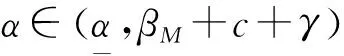
4 模型分析
4.1 不同定价机制下的CSP利润研究


4.2 不同定价机制下的用户剩余研究

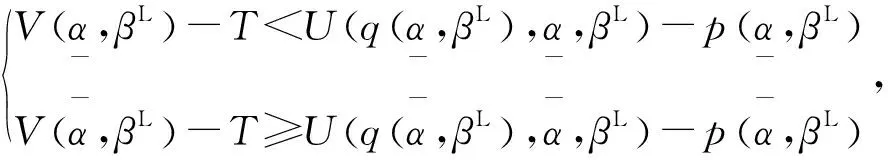

U(q(αu|β=βL,βH),αu|β=βL,βH)
4.3 不同定价机制下的社会福利研究

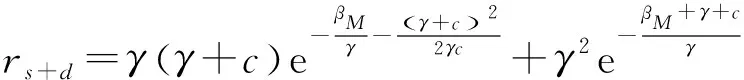

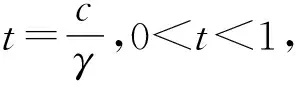

5 结 论
