两种偶氮型分散染料在超临界CO2中溶解度拟合

张 月, 郑环达, 蔡 涛, 郑福尔, 张小海, 郑来久

(1.大连工业大学 辽宁省超临界二氧化碳无水染色重点实验室,大连 116034; 2.辽东学院 服装与纺织学院,辽宁 丹东 118003;3.石狮市中纺学服装及配饰产业研究院,福建 泉州 362700; 4.晋江国盛新材料科技有限公司,福建 泉州 362200)

超临界CO2流体作为一种环保型介质,具有高扩散性和强溶解性,在萃取[1]、表面改性[2-3]和染色[4-7]等染整领域应用价值极大;又因其染色过程无染色废水、染料利用率高、染色流程短、生产能耗低,作为潜在的水浴染色替代技术被广泛关注[8-9]。在超临界CO2染色过程中,染料的溶解行为影响了其在纤维、纱线和织物上的吸附、扩散、染色、拼色、配色性能及工艺设计优化,从而影响了纺织品的染色质量。虽然关于染料溶解度的研究已有文献报道,但由于测试方法、仪器设备、拟合模型等存在较大差异,不能完全用于指导生产实践。为提高纺织品无水染色加工质量,加快实现超临界CO2无水染色工业化,探究染料在超临界CO2中的溶解性能及建立不同种类染料的溶解度数据库至关重要。

染料溶解度测试方法有静态、动态和原位在线监测法等[10]。郑金花[11]采用静态测试法在343.2～403.2 K、10～26 MPa条件下探究了C.I.分散红54的溶解度,并选用Chrastil和MST模型进行拟合;结果表明:Chrastil模型计算得到的平均相对偏差(AARD%)为6.92%,优于MST模型的15.33%;但该法测定染料溶解度存在溶解平衡时间长,取样过程易产生误差,人力和物力消耗大等劣势,故未广泛应用[12]。原位在线监测是将超临界流体设备的高压腔体与红外光谱[13]、拉曼光谱[14]、紫外—可见分光光度计[15]等仪器连接,在超临界状态下通过可视窗口原位监测染料的溶解度;该法虽然提高了溶解度的测试精度,但对实验仪器的校正精度要求高,依赖的流体密度状态方程参数较多且计算复杂,需进一步研究。动态法因取样过程简单及平衡时间短等突出优势,广泛应用于染料溶解度的测定[16-17]。

C.I.分散红54是一种给色量高,匀染性好,色牢度适中,耐酸碱性好的偶氮类染料;其与C.I.分散蓝79的分子结构均相对简单、相对分子质量小、疏水性强,常用于涤纶纤维、纱线和织物的超临界CO2无水染色[8,18]。然而,现有关于C.I.分散红54和C.I.分散蓝79溶解度的测定和模型拟合的文献较少。因此,本文通过动态法测量C.I.分散红54和C.I.分散蓝79的溶解度,探究了超临界体系温度、压力及染料分子结构对染料溶解性的影响,选取Chrastil、MST、Bartle、K-J和SS五种经验方程对实验数据进行拟合,并建立溶解度预测模型,为完善分散染料溶解度数据库和加快实现超临界CO2无水染色工业化提供理论指导。

1 实 验

1.1 材料与设备

未加任何助剂的C.I.分散红54和C.I.分散蓝79(浙江龙盛集团股份有限公司),CO2(纯度>99%)(中昊光明化工研究设计院有限公司),超临界CO2无水染色装置(实验室自制)。染料和CO2的主要特征量及结构如表1所示。

表1 染料和CO2的主要特征Tab.1 Main characters of dyes and CO2

1.2 过程与方法

1) 实验准备:称取烘干至恒重的染料0.3 g(精确至0.000 1 g)放入筛网中,称量并记录总质量为m0;将筛网置于釜底密封,设定实验所需温度和压力。

2) 实验过程:如图1所示,CO2气体(a)通过冷凝器(b)和压力泵(c)液化并加压至临界压力以上,经加热器(d)加热至设定的温度,染料在超临界体系中溶解至平衡。在实验过程中,CO2气体以20 g/min流速不断通入,为了维持系统压力,超临界CO2流体经分离釜(f)从背压阀(k)排出。实验结束后,关闭加热加压按钮,系统中的压力经排气阀(i)缓慢释放[17,19]。

3) 实验结束;将筛网取出烘干至恒重,记为m1。

本文在正式测定C.I.分散红54和C.I.分散蓝79溶解度实验之前进行了预实验,在353.15 K、24 MPa、10～100 min条件下测定两种染料的溶解平衡时间均为60 min。

图1 实验装置示意Fig.1 Schematic diagram of experimental apparatus

1.3 测试与表征

根据染料在超临界CO2中溶解前后质量变化(md=m0-m1),采用差量法计算C.I.分散红54和C.I.分散蓝79的溶解度,计算如下式所示[17,19-20]。

(1)

式中:y为染料溶解度,mol/mol;md为染料溶解质量,g;Md为染料相对分子质量,g/mol;mc为CO2质量,流速(20 g/min)与时间(60 min)的乘积,1 200 g;Mc为CO2相对分子质量,44 g/mol。

2 结果与分析

2.1 温度对染料溶解度的影响

在超临界体系中,温度对CO2密度和染料的饱和蒸汽压影响较为复杂,两者在不同温度下存在竞争关系,因此温度对染料溶解度的影响具有两面性[11,21]。在压力一定条件下,CO2的密度随着超临界体系温度的升高而减小,分子间距逐渐增大,染料和CO2分子的相互作用降低,溶解度降低;另一方面,随着升高温度,固态染料的饱和蒸汽压增大,染料和CO2分子间的相互作用得到加强,溶解度随之升高[22]。低压区时,温度对CO2密度影响高于对染料饱和蒸汽压的影响;高压区时,染料的饱和蒸汽压对溶解度影响更为显著;而溶解度变化趋势发生转变的点(或区域),即为“转变压力”[11,21-22]。此外,随着温度升高,溶质和溶剂分子的热运动增加,使得固态染料更易于以分子状态进入溶剂介质,染料溶解度也得到提升[23]。

如表2所示,在353.15～393.15 K、12～24 MPa、平衡时间为60 min的条件下,C.I.分散红54在超临界CO2中的溶解度在0.57×10-6～10.16×10-6mol/mol内变化,C.I.分散蓝79的溶解度在0.08×10-6～7.16×10-6mol/mol内变化。在24 MPa、353.15～393.15 K时,C.I.分散红54的溶解度由5.05×10-6mol/mol升高到10.16×10-6mol/mol;表明恒定压力下,随着温度升高C.I.分散红54在流体中的溶解度不断增大,且在实验温度和压力范围内未出现压力转变点。C.I.分散蓝79的溶解度与温度的关系较为复杂。当压力小于22 MPa时,C.I.分散蓝79的溶解度随温度的升高而降低;这是因为随着温度升高,CO2密度降低,染料与CO2分子间的相互作用减小,溶解度随之减小。当压力在22～24 MPa时,C.I.分散蓝79的溶解度随压力的升高先增后减,这与温度对CO2密度和染料饱和蒸汽压两方面的作用有关;当温度低于373.15 K时,随着温度升高,C.I.分散蓝79的饱和蒸汽压增加,溶解在体系中染料量增多,溶解度上升,并在373.15 K时溶解度达到最大。

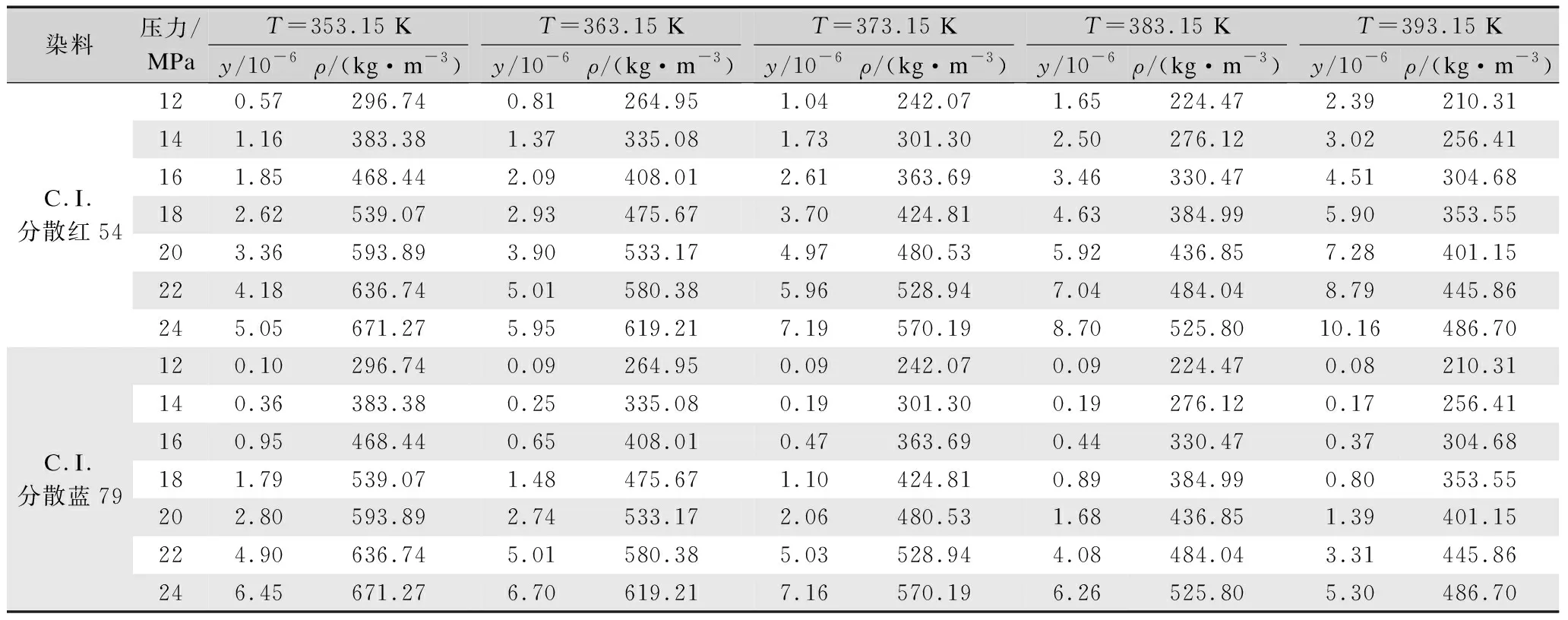
表2 染料在不同超临界CO2条件下的溶解度和CO2密度Tab.2 Solubility and CO2 density of dyes under different supercritical CO2 conditions

2.2 压力对染料溶解度的影响

压力也是影响染料溶解度的重要因素之一[24-25]。当温度一定时,压力从12 MPa升高至24 MPa,两种染料的溶解度均随系统压力的升高呈增加趋势。在393.15 K、24 MPa时,C.I.分散红54在超临界CO2中的溶解度高达10.16×10-6mol/mol;在373.15 K、24 MPa时,C.I.分散蓝79的溶解度达最大值7.16×10-6mol/mol。此外,在12～16 MPa时,C.I.分散红54的溶解度随压力的升高增加缓慢;当压力达到18 MPa时,染料的溶解度增加显著;C.I.分散蓝79的溶解度也在低压时增加缓慢,当压力达到20 MPa时增加幅度较大。这是因为CO2密度与体系的压力呈正相关,随着体系压力增大,CO2介质密度提高。如表2所示,在393.15 K时,压力从12 MPa升高到24 MPa,CO2密度由210.31 kg/m3增大到486.70 kg/m3;而CO2密度的增加,减小了CO2分子与染料分子间的间距,缩短了传质距离,加强了CO2分子与溶质分子间的相互作用,染料的溶解度随之增加。

2.3 染料分子结构对溶解度的影响

染料的分子极性、苯环上取代基团种类及相对分子质量大小等结构因素都会影响其在超临界CO2中溶解度的大小[26-27]。对比两种分散染料溶解度数据可知,C.I.分散红54的溶解度总体上高于C.I.分散蓝79。从分子结构上看,两种染料均为偶氮类染料,基本结构相似,但连接在苯环上的基团及其数量存在差异。与C.I.分散红54相比,C.I.分散蓝79在苯环上连接了—NO2,—OC2H5和—NHCOCH3等极性基团(极性大小:—OC2H5<—NO2<—NHCOCH3),根据相似相容的原理,极性大的染料溶解度小[28-29]。此外,前者的相对分子质量为415.88 g/mol,小于后者相对分子质量639.41 g/mol,而相对分子质量越小有利于溶解度增加[22]。因此,C.I.分散红54的溶解度相对较好。

2.4 溶解度模型拟合

溶解度模型可用于预测、检验及校正实验范围内外染料的溶解度[30-31],根据有限的溶解度实验数据建立精准的溶解度方程,常用的溶解度模型有压缩气体、膨胀流体、计算机模拟及经验模型4大类。经验模型以实验中的温度、压力和CO2密度为变量,采用优化方法对有限的实验数据进行关联,得到可以预测实验范围内溶解度数据的经验方程[21],因其所用溶质的物性参数少且关联效果好而被广泛应用于关联和预测溶质的溶解度[32-33]。应用较多的经验模型有Chrastil、MST、Bartle、K-J和SS模型,以上经验模型可以将溶解度与温度和密度紧密地关联起来[34]。本文选用以上经验模型探究C.I.分散红54和C.I.分散蓝79在超临界体系中的溶解性能,通过对有限的溶解度数据进行拟合,建立溶解度模型,用于检验和预测在353.15～393.15 K、12～24 MPa内染料的溶解度。

2.4.1 平均相对偏差的计算

染料在超临界CO2中溶解度模型的拟合效果用平均相对偏差(AARD值)表示,即染料溶解度的实验值与计算值间的平均相对偏差,AARD值越小,曲线的拟合精度越好,计算如下式所示[19-20,34]。

(2)

式中:AARD表示平均相对偏差;N表示实验点;yexp表示溶解度的实验值;ycal表示溶解度的计算值。

2.4.2 Chrastil模型拟合

Christil模型是研究最早且应用最广泛的溶解度经验模型,表示在超临界CO2体系中溶质与溶剂间的关系,如下式所示。

(3)

式中:a、b、k为Chrastil模型的参数,由实验数据多元线性回归得到;ρ为CO2的密度,kg/m3;T为系统温度,K。

根据Chrastil模型关联拟合得到的C.I.分散红54和C.I.分散蓝79的溶解度，预测方程分别如下式所示。

(4)

(5)

根据式(2)计算得到两种染料的平均相对偏差AARD值分别为6.74%和12.92%。将表2数据代入式(3),得到以lnρ为横坐标、以lny为纵坐标的拟合曲线,且两种染料lny值均随lnρ的增加而增加,如图2所示。C.I.分散红54和C.I.分散蓝79对应的Chrastil模型总体拟合水平R2分别为0.98和0.99,而R2数值越接近于1,代表拟合效果越好,因此两种染料的拟合效果均较好。

2.4.3 MST模型拟合

MST模型可得到溶解度与温度、压力和CO2密度之间的关系,如下式所示。

Tln(yP)=A1+A2ρ+A3T

(6)

式中:A1、A2、A3为MST模型的经验常数;P为系统的压力,MPa。

根据MST模型关联拟合得到的C.I.分散红54和C.I.分散蓝79的溶解度，预测方程分别如下式所示,AARD值分别为7.74%和24.90%。

Tln(yP)=-8 579.145+2.802ρ+10.073T

(7)

Tln(yP)=-8 660.904+5.523ρ+5.931T

(8)

将表2数据代入式(6),得到超临界CO2密度与Tln(yP)-A3T的关系,拟合曲线如图3所示。由图3 MST模型的拟合结果显示,两种染料的溶解度均随CO2密度的增加而增大,都显示出在中等密度区(300～500 kg/m3)实验数据点与曲线吻合稍好于低高密度区。两种染料对应的MST模型拟合水平R2分别为0.99和0.97,拟合效果均较好。

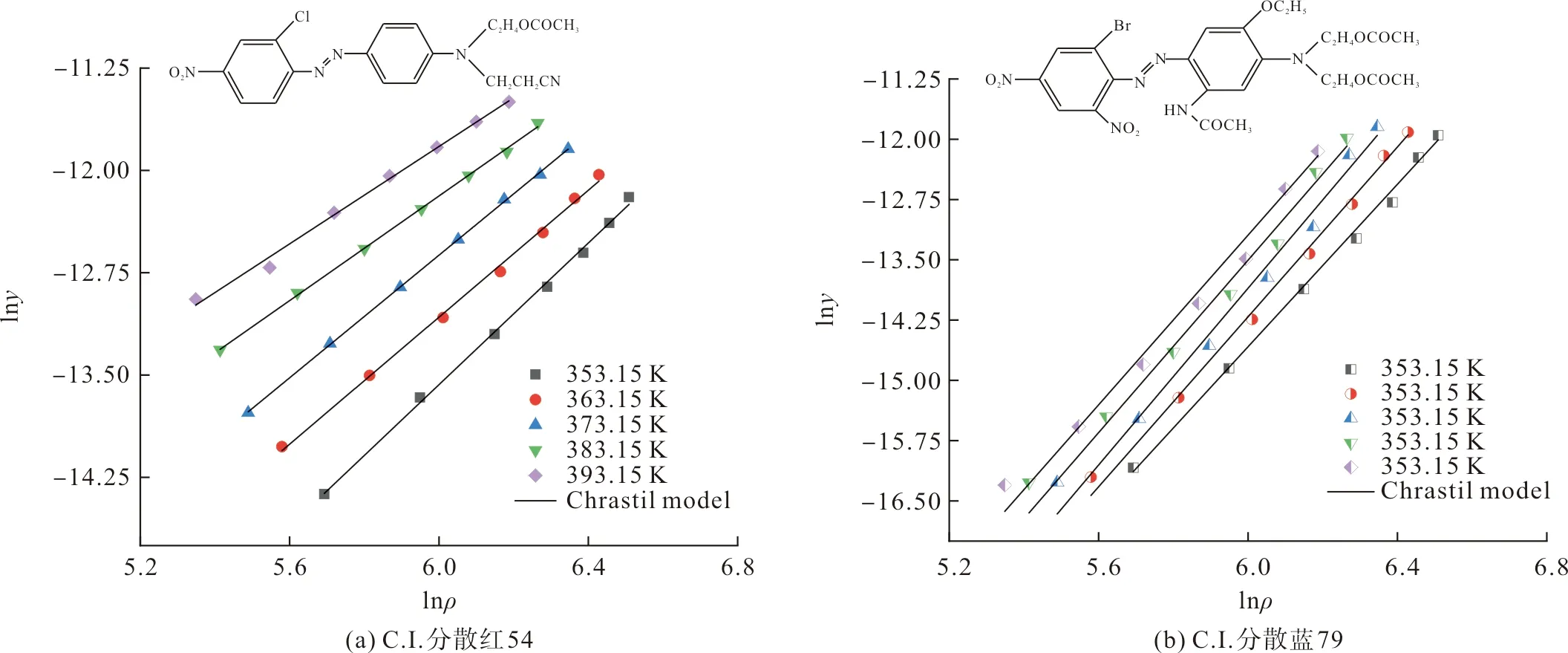
图2 Chrastil模型拟合曲线Fig.2 Correlation curves of the Chrastil model

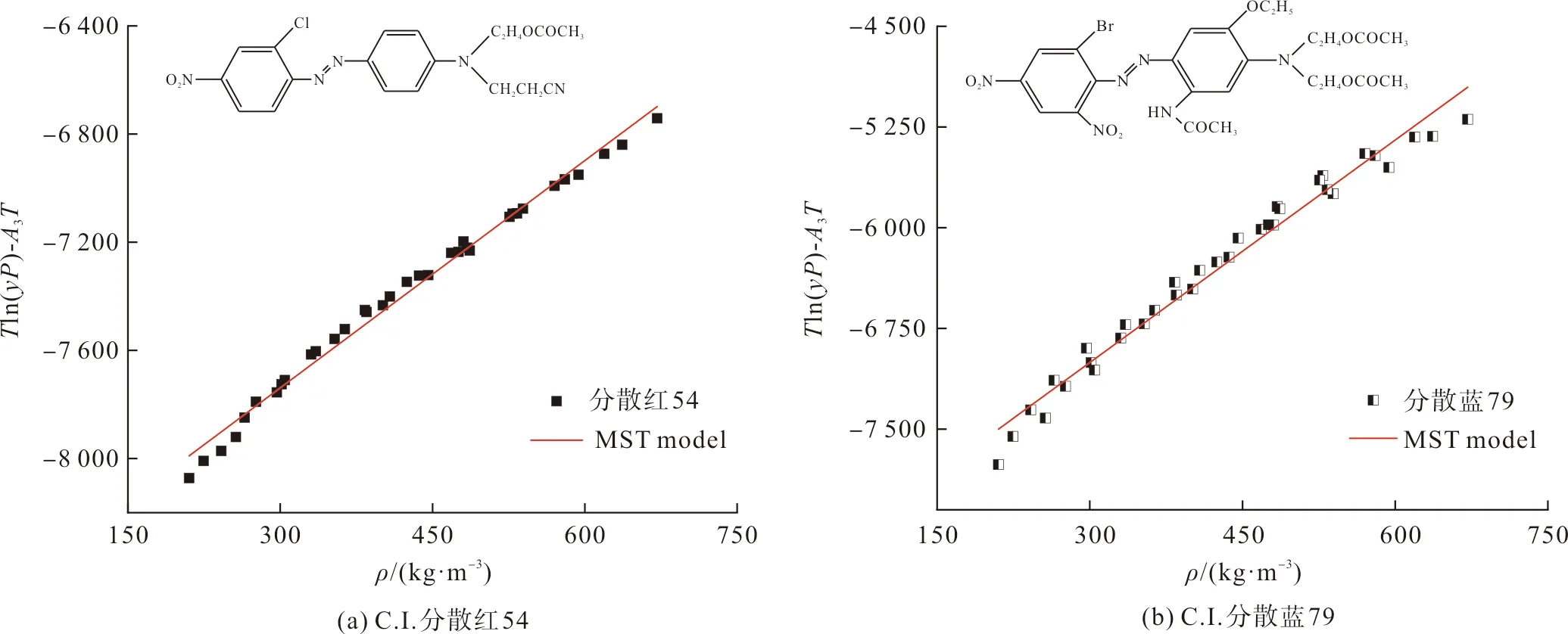
图3 MST模型拟合曲线Fig.3 Relevant curves of the MST model

2.4.4 Bartle模型拟合

Bartle模型通过引入参考压力和参考密度来表达溶解度与温度和密度的关系,如下式所示。

(9)

式中:a、b、c为Bartle模型参数;Pref为参考压力,0.1 MPa;ρref为CO2参考密度,700 kg/m3。

根据Bartle模型关联拟合得到的C.I.分散红54和C.I.分散蓝79溶解度,预测方程分别如下式所示,AARD值分别为6.96%和19.04%。

(10)

(11)

将表2数据代入式(9),得到以ρ-ρref为横坐标、以ln(yP/Pref)为纵坐标的拟合曲线,且ln(yP/Pref)均随ρ-ρref的增加而增加,如图4所示。两种染料Bartle模型的总体拟合水平R2分别为0.99和0.98,拟合效果均较好。

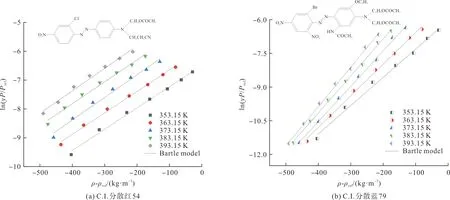
图4 Bartle模型拟合曲线Fig.4 Correlation curves of the Bartle model

2.4.5 K-J模型拟合

K-J模型描述溶解度与温度和密度的关系,如下式所示。

(12)

式中:A、B、C为K-J模型的经验常数,由实验数据拟合得到。

根据K-J模型关联拟合得到的C.I.分散红54和C.I.分散蓝79溶解度,预测方程分别如下式所示,AARD值分别为5.98%和16.82%。

(13)

(14)

将表2数据代入式(12),得到以CO2密度为横坐标、以lny为纵坐标的拟合曲线,如图5所示。两种偶氮型染料lny值均随超临界CO2密度的增加而增大。K-J模型的总体拟合水平R2分别为0.99和0.98,曲线拟合效果较好。

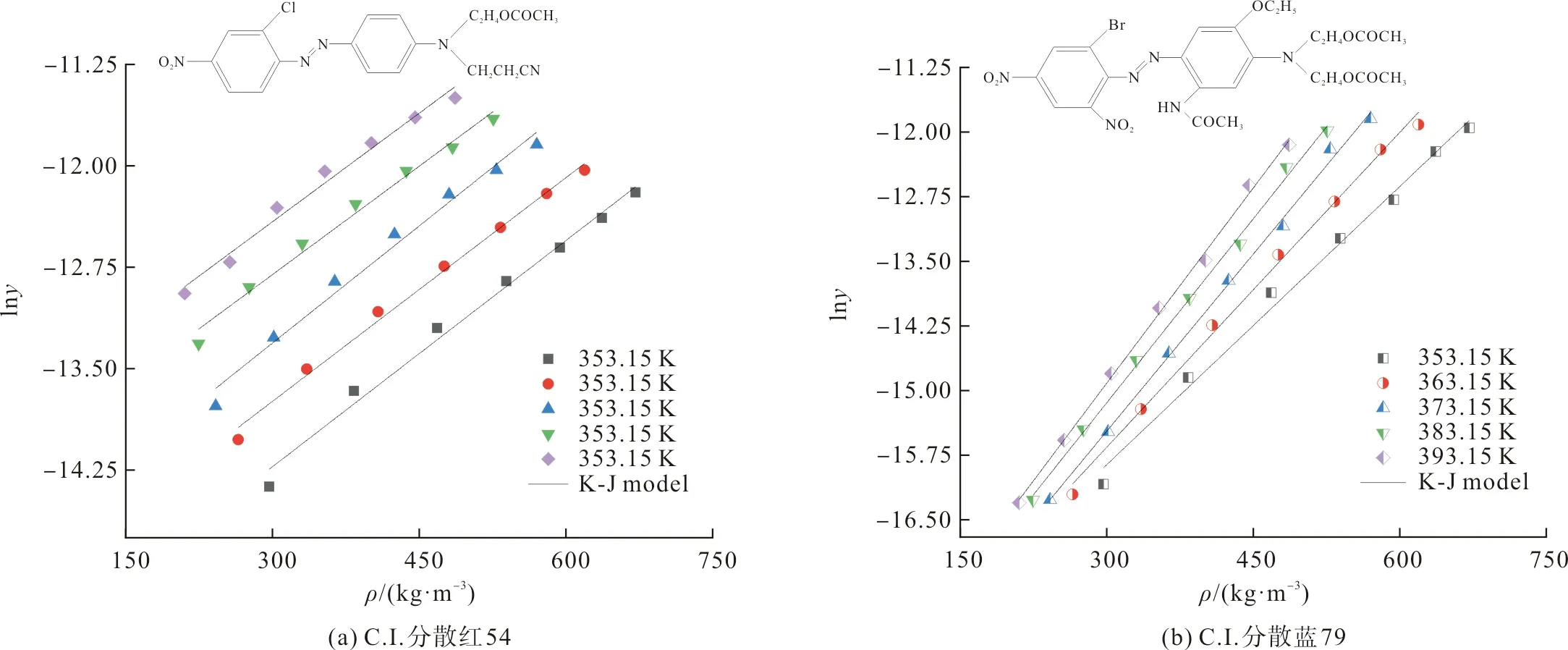
图5 K-J模型拟合曲线Fig.5 Correlation curves of the K-J model

2.4.6 SS模型拟合

SS模型是经Chrastil模型多次修正而得,如下式所示。

(15)

式中:a、b、c、d为SS模型的经验常数,由实验数据拟合得到。

根据SS模型关联拟合得到的C.I.分散红54和C.I.分散蓝79溶解度,预测方程分别如下式所示,AARD值分别为2.88%和12.92%。

(16)

(17)

将表2数据代入式(15),其拟合曲线与Chrastil拟合曲线相同,也是描述lnρ与lny之间的关系,且lny随lnρ的增加而增加,如图6所示。C.I.分散红54的SS模型总体拟合水平R2为0.997,约为1,拟合效果最好;C.I.分散蓝79的总体拟合水平为0.99,拟合效果也较好。

由图2—图6可知,Chrastil、MST、Bartle、K-J和SS经验模型的拟合曲线与C.I.分散红54和C.I.分散蓝79在超临界CO2中溶解度实验数据点基本吻合。由C.I.分散红54溶解度模型的拟合结果可知,Chrastil、MST、Bartle、K-J和SS模型的AARD值分别为6.74%、7.74%、6.96%、5.98%和2.88%,C.I.分散蓝79的溶解度模型拟合后的AARD值分别为12.92%、24.90%、19.04%、16.82%和12.92%;表明C.I.分散红54的SS模型预测的溶解度数值及C.I.分散蓝79的Chrastil和SS模型预测的溶解度数值,分别与两种染料溶解度实验值相关性最好。此外,与测定C.I.分散红54的文献[11]相比,本文中Chrastil模型计算得到的AARD值为6.74%,略小于文献中同种模型AARD值6.92%;选用MST模型计算AARD值为7.74%,远小于文献中同种模型AARD值15.33%。与测定C.I.分散蓝79的文献[35]相比,本文中Chrastil模型计算得到的AARD值为12.92%,远小于文献中同种模型AARD值27.70%;选用K-J模型计算AARD值为16.82%,小于文献中同种模型AARD值17.20%;选用SS模型计算AARD值为12.92%,远小于文献中同种模型AARD值21.10%。因此,本文所得到的C.I.分散红54和C.I.分散蓝79的溶解度数据具有较高的可靠性。

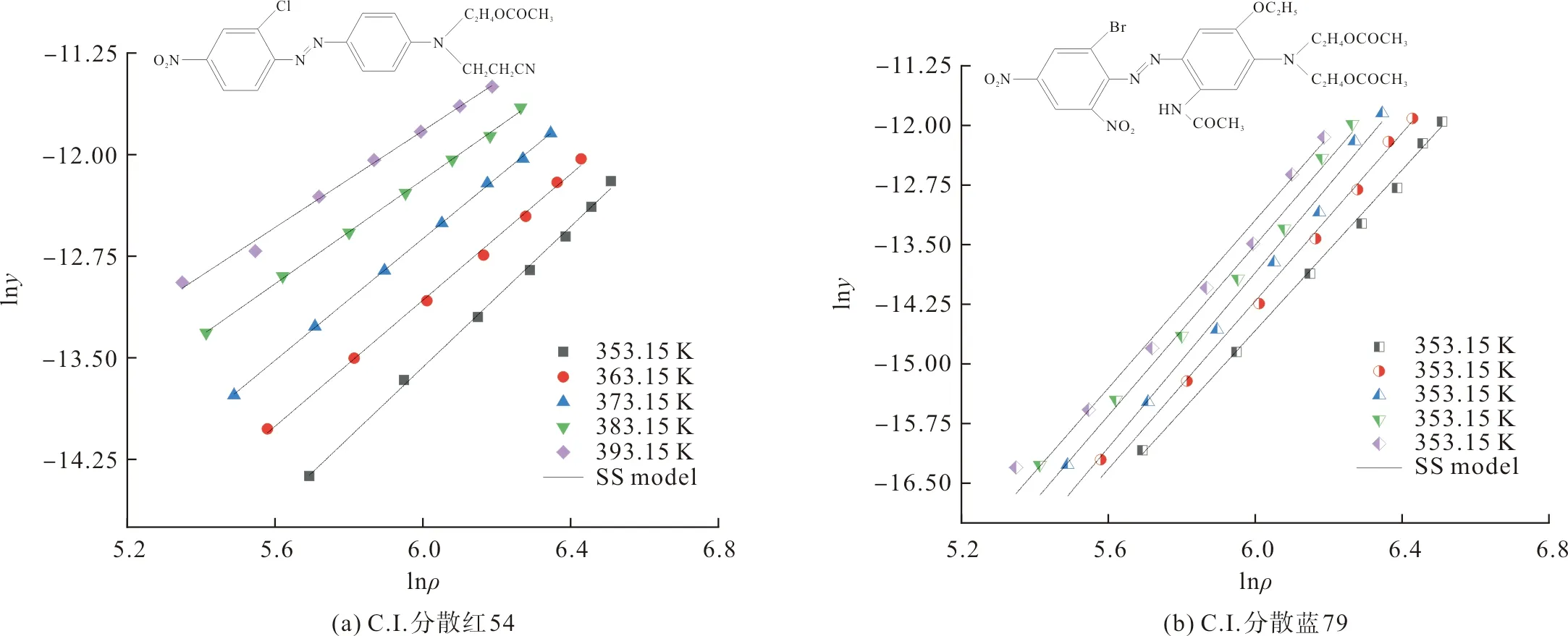
图6 SS模型拟合曲线Fig.6 Correlation curves of the SS model

3 结 论

本文选用动态法测定了C.I.分散红54和C.I.分散蓝79的溶解度,分析了影响其溶解度大小的因素,并选用五种经验模型对溶解度数据进行了拟合,得到如下结论。

1) 两种分散染料在超临界CO2中的溶解度均随压力的升高而增大。

2) C.I.分散红54在温度为393.15 K、压力为24 MPa时溶解度达最大值10.16×10-6mol/mol;C.I.分散蓝79在373.15 K、24 MPa时溶解度达最大值7.16×10-6mol/mol。

3) 经Chrastil、MST、Bartle、K-J和SS模型拟合后,C.I.分散红54的AARD值分别为6.74%、7.74%、6.96%、5.98%和2.88%;C.I.分散蓝79的AARD值分别为12.92%、24.90%、19.04%、16.82%和12.92%;表明SS模型对两种分散染料溶解度的拟合效果均较好,其模型预测的溶解度数值与溶解度实验值相关性较高。与现有文献数据对比,实验的可信度较高。

《丝绸》官网下载

中国知网下载