具有隐私保护的车联网边缘计算任务卸载资源分配策略
2023-02-21王艳阁奚建清
王艳阁,奚建清
(1.郑州经贸学院 计算机与人工智能学院,河南 郑州 451191; 2.华南理工大学 软件学院,广东 广州 510640)
0 引 言
近年来移动互联网迅速崛起,加之通信技术迭代更新速度不断加快使得万物互联成为了热点[1],物互联的体验感与网络性能有着直接关系[2]。虽然无线设备(wireless devices,WDs)的CPU计算能力越来越强大,但是要在短时间内完成这些复杂应用的数据处理仍然是不可能的[3,4]。此外,在本地进行数据处理也面临着高能耗的问题[5,6]。为了克服这些难题,有些学者尝试建立了移动边缘计算(mobile edge computing,MEC)技术并且得到了广泛关注[7-10]。
车联网作为万物互联网中最为典型的一种应用方式,对于计算要求也相对更高,合理地在移动边缘计算侧对车联网进行资源管理,可有效实现高效可靠的车联网最优运行[11,12]。文献[13]针对车联网边缘计算资源优化问题的非凸性和NP难性,设计了一种启发式算法——容错粒子群优化算法,用于求解具有时延约束的可靠性最大化问题。文献[14]提出了一种混合多跳边缘计算卸载算法,重点研究了最优多跳边缘计算卸载方法。此外,还建立了一个多跳卸载开销模型来评估性能。文献[15]研究了一个支持边缘计算的云计算中心IOV框架,旨在提高车辆的服务质量。基于蚁群优化算法(ant colony optimization,ACO),提出了一种联合卸载选择策略和计算资源分配策略的优化方法。文献[16]提出了一种仅依赖于车对车(vehicle-to-vehicle,V2V)通信的任务卸载方案。文献[17]提出基于遗传算法的卸载策略(GAOS)。探讨使用了遗传算法中的卸载策略。
上述研究工作只关注于卸载决策和资源分配的问题,而忽略了无线设备电池容量有限的问题。无线供能通信网(wireless powered communication network,WPCN)是一种联合传输的形式,且实现了无线能量和无线信息在不同时间序列中进行传输。本文研究了基于时分多址协议的多用户无线供能移动边缘计算系统的能量效率最大化问题,并提出了基于系统时间、能耗、卸载计算能力和本地计算能力多方面的联合优化方案。本文提出的最优化问题的目标是实现系统能量效率最大化。最后,本文设计了一种基于模拟退火算法的优化算法来解决上述最优化问题。在任务卸载过程中,本文采用时分多址(time-division multiple-access,TDMA)协议来协调多个车辆的任务卸载。该方法能够大大降低与端服务器的压力,并且能够最大程度上的避免数据被泄露。
1 系统模型及问题建模
1.1 系统概述
本文针对无线供能移动边缘计算系统进行研究。如图1所示,该系统包括了3个部分,分别为:移动边缘计算服务器、一个单天线的混合接入点和N个单天线的车辆。其中,混合接入点与移动边缘计算服务器集成在一起。一方面,混合接入点向所有的车载无线设备广播射频信号,从而对无线设备进行充电。另一方面,移动边缘计算服务器通过混合接入点接收车辆端需要卸载的任务。完成计算任务后,移动边缘计算服务器将计算结果发送回车辆。每个车辆中集成了一个射频-直流转换器和一个可充电电池。车载无线设备可以通过转换模块将射频信号转换为电能,并存储在电池中。在该系统中,移动边缘计算服务器集成了一个混合接入点(hybrid access point,HAP),使得WP-MEC系统能够实现许多功能,包括混合接入点向所有车辆广播射频信号,以及移动边缘计算服务器可以通过混合接入点接收到车辆端卸载的任务。

图1 基于时分多址协议的无线供能移动边缘计算系统
大多数物联网移动智能终端内的即时通讯软件在使用时的数据流向如图2所示,终端A将信号传输至终端B,但是信号首先要传输至云端服务器,然后再经其转发进而传输至B,与此同时云端服务器还会向A发送信号已经传输至B的指令。该机制中云端服务器发挥着十分重要的枢纽作用,尽管能够保证信号传输的稳定性,但是在移动终端快速发展的今天,云端服务器的压力将会呈爆炸式增长,对于计算能力的要求也会越来越高,这必然会导致数据风险快速增长。

图2 即时通讯软件数据的流向
针对上述风险,本文建立了面向无线能量传输和无线信息传输的时间块模型。“收集然后传输”协议应用于每个时间块。因此,在该模型中,车辆首先收集能量,然后在每个时间块中执行任务计算操作。边缘设备有两个功能:一是进行数据中转;二是对数据进行加密处理。不仅要对接收的数据进行加密,对于发送的数据也要进行加密,换而言之,边缘设备要对经过该设备的所有数据都进行加密处理,这种方法不仅能够为云端服务器减压,其最大优点是能够保护数据的安全性,防止泄露的发生。本文使用TΓ表示无线信息传输阶段,T(1-Γ) 表示无线能量传输阶段。时间块T中的无线信息传输阶段和无线能量传输阶段需满足式(1)所示的约束条件
T(1-Γ)+TΓ≤T
(1)
1.2 计算模型
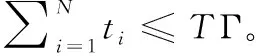
gi=Ad×(di)-αi∈{1,…,N}
(2)
其中,Ad表示天线增益,α表示路径损耗指数,di表示第i个车辆Vi和混合接入点之间的距离。设vi为第i个车辆Vi的传输功率,σ为噪声功率,W为带宽。那么,此时可获得第i个车辆Vi的上行链路卸载速率(比特每秒),如式(3)所示
(3)
根据式(3)可计算得出第i个车辆Vi的卸载能力,即第i个车辆Vi可卸载的比特数为
Coff,i=Roff,i×tii∈{1,…,N}
(4)
考虑到移动边缘计算服务器的计算能力限制,任务卸载能力Coff,i也需满足如下约束
Coff,i≤MCoff
(5)
其中,MCoff代表着移动边缘计算服务器处理车辆Vi端卸载任务时可处理的最大比特数。那么,此时可获得车辆Vi进行任务卸载的能耗,如式(6)所示
ECoff,i=(vi×ti)+(cp×ti)i∈{1,…,N}
(6)
其中,vi表示车辆Vi的信号传输功率,cp表示数模转换器的恒常功率值。
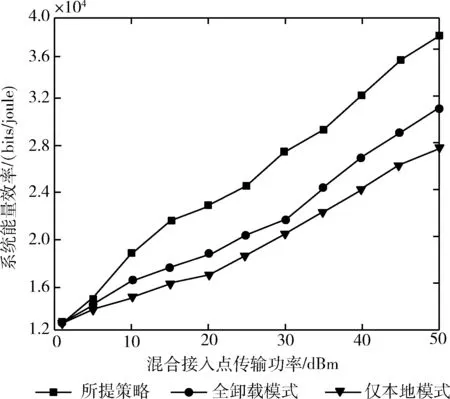
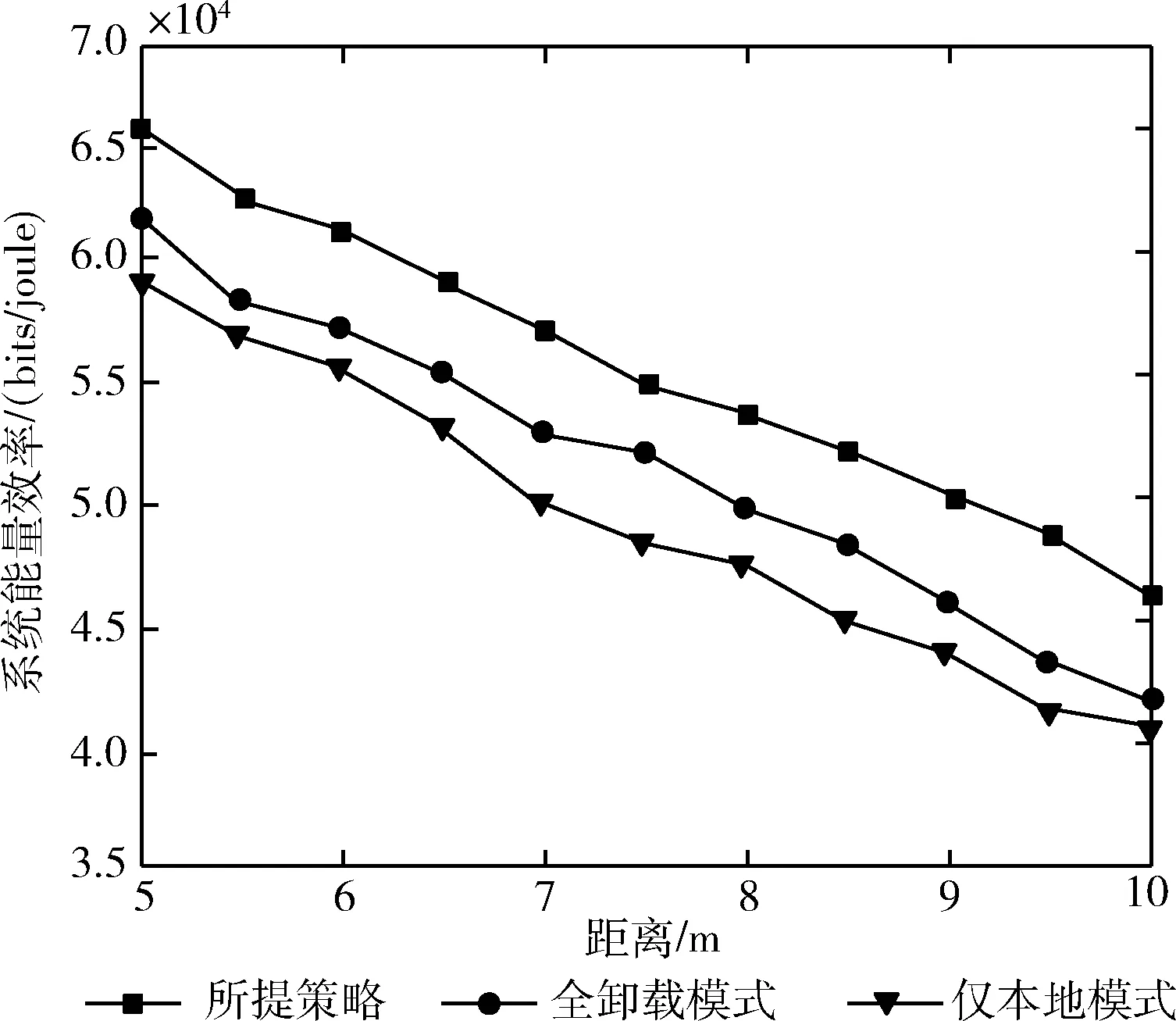
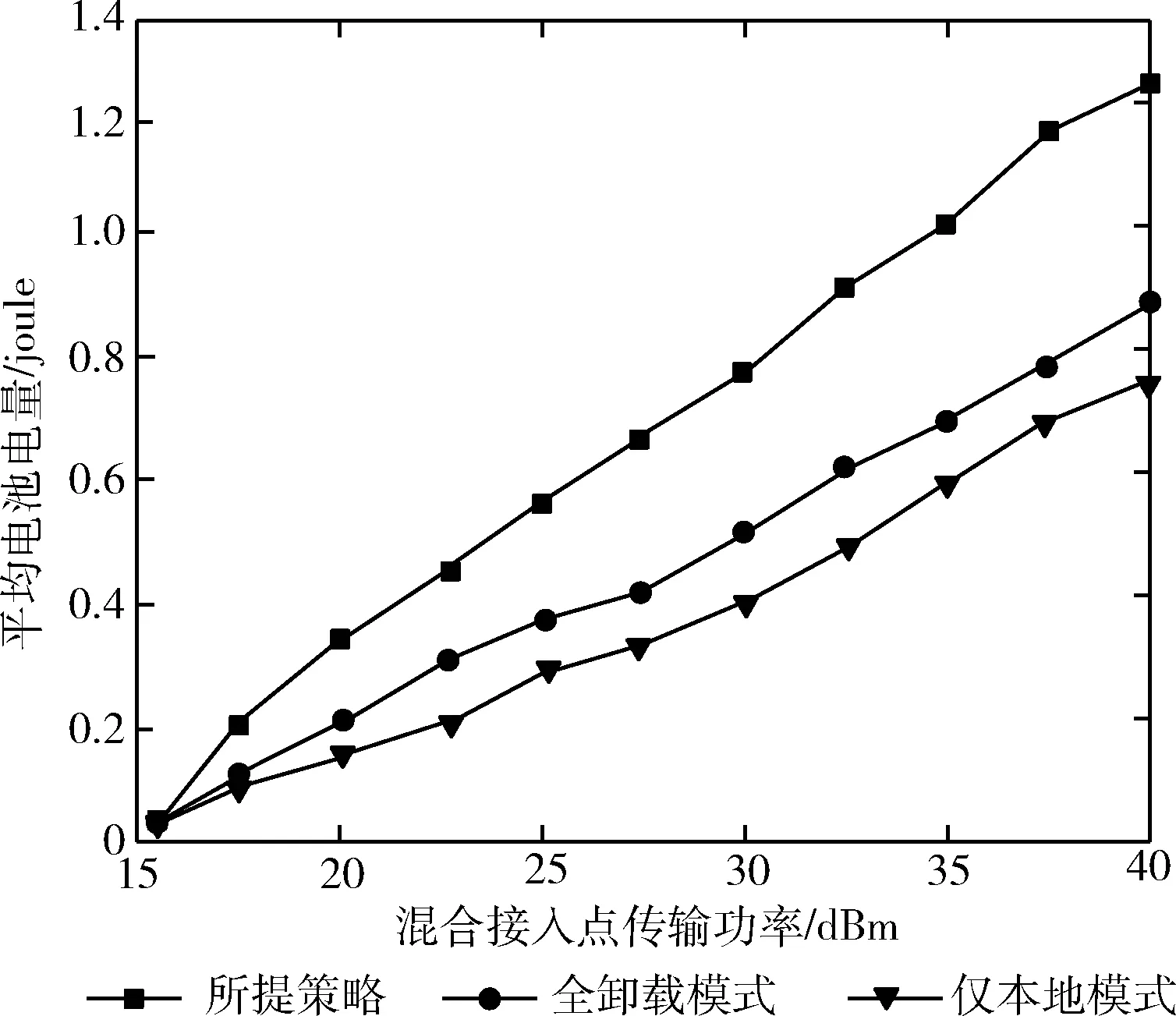
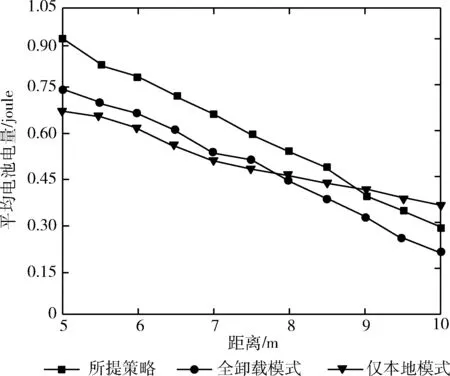
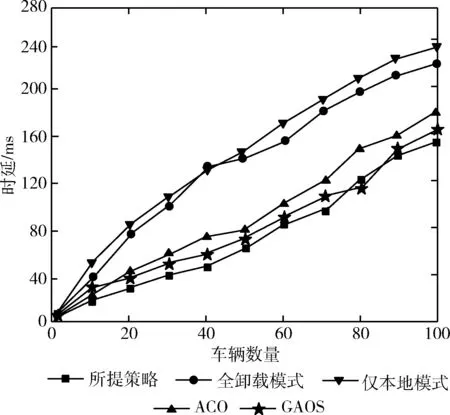
由于本地计算操作需要在时间段T内进行,本文使用lti表示车辆Vi的本地计算时间。其中,lti需满足一定约束条件,即0 (7) 由于车辆的计算资源是有限的,本文使用MCloc,i表示车辆Vi可以处理的最大比特数。那么,车辆Vi的本地计算能力Cloc,i需要满足以下约束条件 Cloc,i≤MCloc,i (8) 根据式(7),车辆Vi本地计算速率可计算为 (9) 本地计算的能耗可以计算为 (10) 其中,li为车辆Vi处理器芯片的能效系数。 本文假设所有的信道状态信息都是已知的。那么,车辆Vi所获得的能量就可计算为 (11) (12) bti是在时间块T中,车辆Vi的电池电量水平(即剩余电池电量)。由于车辆需要维持其射频信号接收和能量转换的基本功能,本文设定电池电量水平bti≥0。 为了保证车辆Vi能够连续工作,车辆Vi进行任务卸载和进行任务本地计算的能耗之和ECloc,i+ECoff,i不能超过车辆Vi收集的能量和车辆Vi电池中剩余的能量之和Ei+bti。 那么,车辆Vi的能耗需满足以下约束 ECloc,i+ECoff,i≤Eharvest,i+bti (13) 在此方法中,电池性能主要受两个方面影响,即电池充电和电池电量水平。因此,本文从这两个方面来讨论电池的性能表现。 (2)电池电量水平:一方面,无线设备的电池电量水平与无线设备的能耗成反比关系。主要原因为,当无线信道增益为gi, 且无线设备收集到的能量Eharvest,i为常数时,如果无线设备的能耗ECloc,i+ECoff,i越高,那么车载无线设备电池的剩余能量越低,即电池电量越低。另一方面,电池电量水平与无线设备收集到的能量成正比关系。主要原因为,当车载无线设备的能耗ECloc,i+ECoff,i为常数时,如果无线设备收集的能量越多,那么无线设备的电池积累的能量越多,电池电量就越高。 本文主要研究了能量效率的最大化问题。在针对该最优化问题建模时需考虑上行链路卸载率、本地计算速率、所有车辆的总能耗以及混合接入点的能耗等多个方面。设移动边缘计算服务器的任务量占总任务量的比例因子为α, 本地执行的任务量比例因子为β。 基于式(6)、式(10)以及式(12),无线供能移动边缘计算系统的总能耗可建模为 (14) 根据式(3)和式(9),无线供能移动边缘计算系统的计算速率为任务卸载率与本地计算速率之和,可计算为 (15) 最后,基于系统计算速率和系统能耗,本文针对系统最大能效问题进行了建模。该最优化问题与任务计算时间分配、车辆的本地计算能力和卸载能力、车辆获取得到的能量以及能量消耗等多个方面有关。该系统能效最大化问题可如式(16)和式(17)所示实现问题模型的建立 (16) (17) 其中,t=[t1,t2,…,tn],lt=[lt1,lt2,…,ltn]。C1和C2分别是针对本地计算时间和任务卸载时间的约束条件,C3和C4分别是针对卸载能力和本地计算能力的时间约束条件,C5是针对能量的约束条件。 由于上述优化模型的优化目标与约束条件之间存在非线性关系,求解较为困难,故采用模拟退火算法对优化模型进行求解。 (18) 其中,p为接受当前解为最优解的概率,可表达为 (19) 式中:φ为玻尔特兹曼常数。 算法过程如算法1所示。 算法1:模拟退火算法 (1)初始化:高温Tmax=100、 温度下限Tmin=1 (2)设当前状态处于最高温,即T(k)=100 (4) 将S1={α1,β1} 赋值给最佳解S*={α*,β*} (5) 初始化当前温度下的迭代次数L=100 接受当前解为最优解,并将S′={α′,β′} 赋值给最佳解S*={α*,β*}; Else 以metropolis准则中的概率p接受S′={α′,β′} 作为当前最优解 End if Ifm=L End if Else 返回(6) (8)T(k+1)≤αT(k) IfT(k+1)≤Tmin End if Else 返回(6) 在这一章中,本文进行了仿真模拟实验,并根据仿真模拟实验结果对本文提出的算法进行了性能评估。 以下4种算法作为该算法的基准算法: (1)全卸载模式:无线设备只能利用将计算任务卸载到移动边缘计算服务器进而完成其计算任务。 (2)仅本地计算模式:无线设备仅选择在本地执行任务计算。 (3)文献[15]提出的蚁群优化算法(ant colony optimization,ACO),该算法是一种联合卸载选择策略和计算资源分配策略的优化方法。 (4)文献[17]所尝试的基于遗传算法中的卸载策略。这种算法就是通过对不同车速需求、不同MEC覆盖需求等分配不同的优先级,再对不同优先级设置相应的权重,该方法经验证效果较好。 本次仿真模拟实验的系统参数设置具体见表1。 表1 系统参数设置 3.2.1 系统能量效率性能对比 如图3所示,本文通过改变N的值来研究不同的车辆数量对系统能量效率的影响。如图3所示,与全卸载模式、仅本地计算模式相比,所提策略的系统能量效率比上述两种模式均提高了15%以上。在3种模式中,系统能量效率都随着N的增加而增加。这是因为N的增加意味着在任务计算过程中涉及的车辆越多,从而导致系统能量效率的增加。 图3 不同的车辆数量对系统能量效率的影响 如图4所示,本文通过改变tp的值来研究不同的混合接入点传输功率tp对系统能量效率的影响。从图4中可知,与全卸载模式、仅本地计算模式相比,所提策略的系统能量效率比上述两种模式均提高了20%以上。此外,在3种模式中,系统能量效率都随着tp的增加而增加。主要原因为,当tp越高时,车辆Vi收集到的能量越多,使得车辆有足够的能量来执行任务计算,从而提高了系统的能量效率。 图4 不同的混合接入点传输功率对系统能量效率的影响 图5 混合接入点与车辆之间不同的平均距离对系统能量效率的影响 如图6所示,本文通过改变tp的值来研究了不同的混合接入点传输功率tp对平均电池电量的影响。从图6中可知,所提策略的平均电池电量比全卸载模式、仅本地计算模式的平均电池电量分别高了40%以上。在3种模式中,平均电池电量都随着tp的增加而增加。这是因为根据式(3),当tp的值越高时,车辆收集到的能量越多,因此车辆电池中剩余的能量也就越多。 图6 不同的混合接入点传输功率对平均电池电量的影响 如图7所示,本文通过改变dA的值来研究了混合接入点与车辆之间的平均距离dA对平均电池电量的影响。从图7中可知,所提策略的平均电池电量比全卸载模式的平均电池电量分别高了20%以上。当距离小于7.5 m时,所提策略的平均电池电量比仅本地计算模式高20%以上;而当距离大于6.5 m时,锁头策略的平均电池电量比仅本地计算模式低10%左右。在3种模式中,平均电池电量都随着dA的增加而降低。这主要是因为dA的增加使得下行链路的能量传输信道情况变差。即根据式(2)和式(3),距离的增加降低了信道增益gi, 从而使得车辆可获得的能量减少,最终导致平均电池电量的降低。 图7 不同的距离对平均电池电量的影响 3.2.2 时延性能对比 图8描述的是不同车辆数量下几种方法的系统平均时延变化情况。可以看到随着车辆数量增加,5种方法的系统平均时延都在不断增大。由于为所提策略在任务卸载过程中,采用时分多址协议来协调多个车辆的任务卸载。这种方法不仅缓解了云端服务器的通信压力。因此相较于对比方法,所提算法系统时延更低。所提写略能够以最优的卸载决定和卸载率进行任务卸载,避免了拥塞情况下的额外时延开销,有效地降低了系统时延。 图8 不同车辆数量下的系统平均时延 提出了一种具有隐私保护的车联网边缘计算任务卸载资源分配策略。本文以移动边缘计算技术为基础,研究了基于计算时间分配、能耗、本地计算能力和卸载计算能力多方面的联合优化问题。此外,为解决这一优化问题,提出了一种基于模拟退火算法的最优化算法。仿真模拟实验结果表明,提出的算法在能量效率方面的表现优于其它基准算法。提出的算法的预期用途是在无线供能移动边缘计算系统的实际应用场景中提高车辆的计算性能。 今后的研究工作将继续从以下几个方面进行: (1)从更多方面对本文提出的算法进行评估。即除了本文使用的评估指标(系统能量效率)外,还将增加更多的测试评估指标,如能耗和系统吞吐量等。 (2)通过将本文所提出的算法应用于实际应用场景以测试其实际性能。可以将计算任务卸载到移动边缘计算服务器上进行任务处理,同时智能家居设备可以收集来自混合接入点的射频能量。那么,通过以上部署可以将本文所提出的算法集成到这些网络设备中,从而运行该系统并测试其实际性能。1.3 能量收集和消耗模型
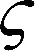
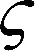

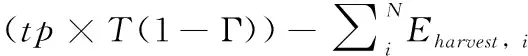
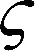
1.4 问题建模


2 一种系统能量效率最大化算法
2.1 建立metropolis准则
2.2 算法流程



3 仿真实验
3.1 基准算法和参数设置

3.2 仿真实验结果


4 结束语
