基于动网格技术水平轴风力机叶片及尾迹流场旋涡特性

高伟，张立茹，2*，姚慧龙，闫蓉

(1. 内蒙古工业大学能源与动力工程学院，内蒙古 呼和浩特 010051； 2. 风能太阳能利用技术教育部重点实验室(内蒙古工业大学)，内蒙古 呼和浩特 010051)

以涡量为特征变量的横过程是单一性质的流体运动中2个基本动力学过程之一[1].来流风在通过旋转风轮后，由压力主导的边界层三维特性在风轮各个位置产生许多体积较小但却极为复杂的涡流结构[2]，然而这些占据了少量空间的涡结构对风力机造成了极大的影响.近年来随着试验水平的提升与仿真技术的革新，国内外对风力机流场中的涡结构进行了诸多研究.

在试验测量方面，利用图像粒子测速法(particle image velocimetry， PIV)对风力机叶尖涡、中心涡进行测量，发现叶尖涡使得风力机近尾迹流场更加混乱、湍流度更高，造成尾迹流场膨胀，风能密度降低[3-4]；中心涡在风力机后方以正负涡成对出现，并且在运动过程中将与叶尖涡混合，会进一步加剧风力机尾迹流场的混乱程度[5-6].但因试验条件的制约，随着计算能力的发展，数值模拟方法也可以对风力机流场分布情况做出预测.在数值模拟方面，目前对于模拟风轮旋转有多种方法，包括制动盘理论、制动线模型、滑移网格方法、动网格方法等.制动盘理论占用计算资源较少，可研究多台风力机之间的相互作用，采用制动盘理论模拟上游风力机对下游风力机的影响，得出上游风力机产生的涡结构将影响下游风力机的发电效率[7]，但制动盘理论并未实现真正的风力机旋转，无法对叶片表面流场进行细节研究；滑移网格方法操作简单，用于探究大型风力机风轮产生中心涡与机舱的相互作用，研究发现中心涡将导致风向标周围流场紊乱，风轮无法正对来流风[8]，然而滑移网格的刚性网格运动面将对风轮表面的三维流动特征造成影响，导致计算精度无法得到保证；动网格方法能够真实模拟风轮在流场中的旋转过程且计算精度较高，运用动网格技术研究风力机叶片振动对风力机尾迹涡的影响，发现叶片振动的加入将导致叶尖涡耗散率的增加[9].

综上所述，在风力机运行过程中，涡在其中起到至关重要的作用，前人已经对风力机尾迹涡进行了较为系统的研究，但由于叶片表面涡不易测量，滑移网格方法计算精度无法保证，动网格方法能够真实地描述风轮在流场中的运动过程，文中将使用动网格方法对风力机叶片表面及尾迹涡团分布和涡量波动等特征进行分析，探究风力机流场中涡的产生及演化规律，以期为风力机旋涡特性的研究提供借鉴和参考.

1 建模及求解

1.1 几何模型

以选用课题组自行设计的水平轴三叶片S翼型风力机为研究对象，其具体参数：风轮直径为1.4 m,额定来流风速10 m/s,风轮转速750 r/min,转轴倾角为0°,风轮锥角为0°,风轮高度1.71 m,额定功率300 W,风轮利用系数为0.42.

使用SolidWorks绘制导流罩和叶片，并将叶片及导流罩进行装配，导入SCDM(space claim)进行模型检查及修复，得到完整风轮模型，如图1所示.以实验室风洞模型作为外流场模型，其长9 m，宽5 m，高5.3 m.

图1 风轮模型图

1.2 网格划分及网格无关性验证

将几何模型导入ICEM进行网格划分.本次计算选择的重叠网格方法需要2套网格来保证网格在运动时能够保持良好的网格质量，以风洞网格为背景网格，选择运动特性更好的非结构网格进行绘制，如图2所示，前景网格为运动区域网格，前景网格尺寸需与背景网格尺寸相近，避免网格运动过程中出现孤儿网格，如图3所示.网格运动过程中网格尺寸较小的网格具有更高优先级，以此保证网格运动过程中能够有较高的网格质量.

图2 背景网格区域

图3 前景网格区域

通过多组计算对网格无关性进行验证，其中具有代表性的5组数据如表1所示，表中N为网格数，其中200万网格、250万网格数量均对风轮输出功率有较大影响，300万网格、350万网格、400万网格数量对风轮输出功率P影响已不明显，所以在不影响计算精度的情况下，为了节约计算资源，更快收敛，选择300万网格进行计算.

表1 网格无关性验证

1.3 边界条件及湍流模型

本次计算选择入口为均匀入流的速度入口(v=10 m/s)，设置压力出口的相对压力为0，风轮表面、地面、壁面均为无滑移边界.通过连续性方程、动量方程(N-S方程)及能量方程作为文中的控制方程对问题进行描述，采用通用性较好的k-ε模型作为该文的湍流模型进行计算.选用SIMPLE算法进行模拟，选择二阶迎风格式以保证计算精度.减小松弛因子以保证计算收敛.瞬态计算过程中，当动量方程速度分量残差小于10-6，连续性方程中湍动能k与湍动能耗散率ε的残差减小到10-4以下，认为计算收敛.

1.4 涡识别方法的选择

目前对涡的研究方法有很多，对比当前较为主流的Q，λ2，△和λci等二代涡识别方法[10]，其中Q准则得到结果不易受到剪切层的影响，相较于其他涡识别方法，Q准则更适合用于流体受剪切较多的风力机涡结构识别，可较为准确地显示风力机尾流场中的涡大小，所以选择Q准则作为本次模拟结果中涡的识别方法.

1.5 数值计算方法有效性验证

为了验证计算结果的有效性，将额定风速下多个不同尖速比λ的风轮输出功率P与试验值进行对比，结果如图4所示.随着叶尖速比的增大，计算值与试验值风轮输出功率增长趋势基本相同，尖速比为6.5时计算结果与试验结果吻合度更高，动网格方法计算风轮输出功率更接近于试验值，由于计算过程中未考虑叶片与塔架相互作用，所以计算输出功率均略高于试验值，该结果表明，文中计算结果有效.

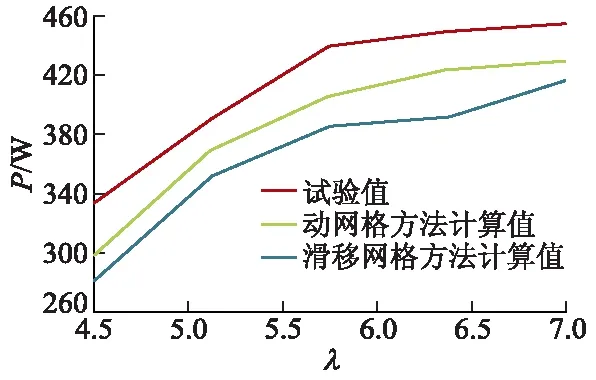
图4 计算功率与试验值对比

2 结果分析

选择与试验值风轮输出功率吻合度更高的尖速比6.5工况计算结果进行分析，探究风力机叶片表面涡的产生以及在离开风轮后涡在尾迹流场中的演化过程.

2.1 叶片表面涡量分析

由于流体微团具有黏性，空气在流经叶片表面时受到逆压，出现流动势能差，形成有旋运动，通过对叶片表面涡量Q分布情况进行研究，能够了解风力机流场中涡的产生，叶片表面涡量分布如图5所示，叶片表面高涡量区域主要集中于叶尖位置与叶片前缘.

图5 叶片表面涡量图

图6为叶片表面压力pr云图.分析图5，6发现，叶片表面压力梯度较大位置与叶片表面高涡量区域一致，所以当气流流过逆压梯度较大的叶片表面区域时，气流需要在短时间内克服较大的逆压，一旦气流动压无法克服叶片表面逆压，叶片表面的流体便会发生边界层分离，较薄的分离层离开叶片表面后在背景流场作用下立刻发生卷绕，并带动附近流体进行旋转，形成了叶片表面的分离涡.

图6 叶片表面压力云图

进一步选取从叶根到叶尖具有代表性意义的典型特征截面对叶片表面分离涡进行分析，如图7所示，并与滑移网格计算结果(见图8)进行对比.

图7 动网格翼型截面流线涡量图

图7为0.3R，0.5R，0.7R，0.9R这4个叶片截面涡量流线图.显然，0.3R处的涡量主要集中在前缘及后缘，随着截面到回转中心距离的增大，涡量明显增大，至0.9R截面处吸力面及前缘、后缘均为高涡量区域，流线在高涡量的带动下密集且混乱.从翼型角度分析，雷诺数Re=ρvL/μ中的特征长度L是翼型的弦长，而速度v为该翼型截面瞬时线速度与来流风速的合速度，不同截面的L与v不尽相同，这也直接导致了不同截面雷诺数有所差别，而雷诺数的值对近壁面流场有显著影响[11]，所以在同一叶片不同位置截面附着涡量不同，涡量分布特征和分离特性也不同.

图8 滑移网格翼型截面流线涡量图

对比相同截面动网格(见图7)与滑移网格(见图8)叶片表面涡量，4个截面中，相较于滑移网格方法，动网格所得云图在吸力面流动分离区域更大，并且随着到回转中心距离的增加，现象愈发明显.但二者的叶片表面计算结果涡量分布趋势基本一致.究其原因，使用滑移网格方法是一种简化风轮旋转的模型，其外部网格静止，内部网格与风轮一同旋转，流体在通过内部面位置会产生较大误差，动网格方法的前景网格与背景网格在导入后将成为一个整体，无交界面的产生，也就避免了误差的出现，所以在滑移网格叶片表面的轴向流动速度较小.由于动网格方法叶片表面轴向流动速度更大，也就导致在相同时间内使用动网格方法计算的叶片表面流体需要克服更大的逆压，故其吸力面前缘及后缘位置发生流动分离区域更大，能够捕捉到叶片表面更多的边界层分离细节，更清晰地展现叶片表面的三维流动特征.

2.2 尾迹涡涡量分析

风力机在叶尖及叶根形成旋涡后，在三维轴状涡的拉伸效应下叶尖涡与中心涡迅速向下游移动，接下来将对风力机流场中涡的演化过程进行研究.图9为尾迹涡涡量云图.图9a中，叶尖涡在脱离风轮后向外膨胀并向后扩散，断断续续呈气泡状向后流动.轮毂后出现呈蝶状的中心涡，沿轴向迅速衰减.相同条件下滑移网格得到的涡量图(见图9b)中，中心涡呈喷射状，叶尖涡呈带状，从图中不难发现动网格所得出的涡量强度要大于滑移网格得出的结果.

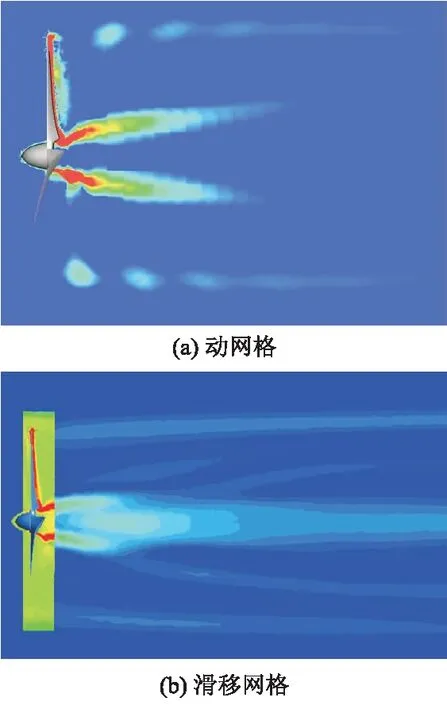
图9 尾迹涡涡量云图

2.2.1 叶尖涡涡量分析

风轮表面分离涡向后运动过程中，可产生叶尖涡与中心涡2个区域[12]，为了明晰叶尖涡在尾迹流场中的运动规律，对叶尖涡区域涡量进行分析，其涡量强度云图如图10所示.图中可以发现，在风轮转动与叶尖涡脱落的双重作用下，叶尖附近形成了大量的高涡量区域，叶片转动带动空气向同方向流动，使得叶尖涡受到叶片转动方向的拉力，故图10中脱离叶片的高涡量区域有向叶片运动方向移动的趋势.叶尖涡在主流场作用下涡线被拉长并逐渐向下游移动，也就有了图8所示的带状高涡量区域，叶尖涡在向下游运动过程中，逐渐出现正负涡核上下错位的叶尖涡“交互跳跃”现象，这与文献[4]所描述试验现象一致，也再一次证明了使用动网格方法计算流场的可靠性.

图10 叶尖涡涡量云图

2.2.2 中心涡涡量分析

在对叶尖涡运动过程有了简单认识后，接着对风轮后中心涡的分布进行分析，选取风轮后4个典型位置的涡量波动特征进行分析，并与相同工况下的滑移网格计算结果进行对比，结果如图11所示.选取风轮后0.1D，0.5D，1.0D，4.0D这4个截面涡量曲线中，横坐标表示径向相对位置(Y=X/D，X为到回转中心距离，D为风轮直径)，0为风轮回转中心位置，-0.5，0.5为叶尖所对应位置.图中中心涡位于横坐标0附近，由图可以看出，在尾迹流场中，中心涡涡量大于叶尖涡涡量，在图中占据主导地位，并且随着轴向距离的增加，中心涡涡量先增加然后急速衰减.

对动网格涡量曲线进行分析，图11a中，在回转中心对称位置有2个峰值，这与前文图9中观察到的轮毂后蝶状中心涡一致，在单侧出现的峰值与风轮的周期性旋转有关.距离风轮后0.5D，在风轮轴向加速度加持下涡量密度增强，涡量峰值再一次增大，中心涡依旧呈现双峰状，中心涡区域没有明显拓宽，中心涡还未发散.图11c中，出现多个峰值，涡量曲线呈波浪形分布，说明在非局部自诱导和主流场的作用下叶尖涡与中心涡已开始混合扩散，这里涡量已开始急剧下降，涡量峰值不到0.5D处的1/2.图11d中，虽然涡量依旧呈现双峰分布，但峰值已不到0.5D处的1/10，气流逐渐趋于平稳.由风轮后的涡量波动特征不难发现，叶片表面分离涡在离开叶片表面后，经过风轮旋转效应的加持，分离涡得到进一步加强，接着继续向下游运动成为尾迹涡，尾迹涡在向后运动过程中失去能量来源，涡核所含能量不断发生损耗，整个旋涡经历高度的非线性失稳，最终涡核破裂，涡流散开.

通过对比动网格与滑移网格尾迹涡量计算结果可发现，4个截面中，动网格涡量峰值均大于滑移网格涡量峰值，相较于动网格，滑移网格于0.5D便出现中心涡区域扩张现象.分析原因，前文提到风轮表面涡量在背景流场的作用下向后脱离风轮表面向后移动，动网格方法无交界面处存在使得计算误差较小，流体轴向速度较大，产生分离涡区域更大，所以动网格方法得到尾迹涡涡量峰值略高于滑移格计算方法结果.并且由于轴向流体速度的误差较大，滑移格方法计算涡量在距离风轮更近的位置出现中心涡扩散现象，但二者在瞬态计算中均有真实的风轮旋转过程，所以涡量分布基本一致.

图11 尾迹涡量曲线图

3 结 论

文中使用动网格方法对风力机流场进行计算，探究涡在风力机流场中的产生与演化，并与滑移网格计算结果进行对比，可得出以下结论：

1) 在叶片表面，从叶根到叶尖涡量逐渐增加，叶根涡量主要集中于前缘与后缘，叶尖部分涡量主要集中在前缘、后缘和吸力面.相较于滑移网格方法，动网格方法计算出叶片吸力面流动分离区域更大，能够捕捉到叶片表面更多的边界层分离细节，并且随着到回转中心距离的增加，该现象愈发显著.

2) 中心涡量分布于风轮后呈双峰状，涡量峰值随着到风轮距离的增加先增大后减小.在0.5D～2.0D内，叶尖涡与中心涡发生混合扩散，4.0D时涡量强度已不及0.5D时的1/10.计算结果中，动网格方法捕捉到涡量大于滑移网格得到结果，并且滑移网格计算结果中心涡扩散位置距离风轮更近.

3) 根据叶片表面涡量及尾迹涡量对比结果，使用动网格计算方法得出的涡量值均高于滑移网格，所以动网格方法能够捕捉到风力机流场中的更多微小旋涡.

相较于文中选取风力机模型，大型风力机具有更高的叶尖速比，所以大型风力机叶片表面更易发生边界层分离，尾迹流场中其涡量分布与大型风力机尾迹流场分布趋势基本一致.