连续急弯对河段输沙能力的累积效应试验研究

吴岳昆，孙 一，侯志军，伊晓燕

（1.郑州大学，河南 郑州 450001；2.黄河水利委员会 黄河水利科学研究院，河南 郑州 450003）

黄河下游河道存在大量的连续急弯，其几何边界的特殊性导致河长增加、水流能量降低、河道输沙能力改变，进而引起一系列水沙问题，给河道治理及沿线人民的生产生活带来了极大的安全隐患。连续急弯河段输沙能力沿程减弱是当下黄河下游河道治理与滩区治理所面临的重要问题［1］。河道边界形态与水沙过程之间的相互作用影响河道输沙能力［2］，对此，学者们进行了大量研究工作［3］。王彦君等［4］研究了主槽断面形态对水沙变化的影响。白玉川等［5］认为通过优化河床断面形态，能够提高河槽的输水输沙能力。刘月兰等［6］在经验公式中以指数的形式描述边界形态与河道输沙能力。Bagnold［7］以河宽作为描述边界形态的指标。孙东坡等［8］以黄河下游实测资料为基础，采用断面形态B／H（B为河宽、H为水深）与来沙系数S／Q（S为含沙量、Q为流量）构造输沙效率综合系数Φ＝（B／H）（S／Q）0.5，认为造床流量时的综合系数Φ最大，河道的输沙效果最佳。程亦菲等［9］通过分析场次洪水，得出断面形态B／H对输沙能力的影响权重大于来沙系数S／Q的权重。由此可见，针对河道输沙能力的研究，多以断面河宽和水深作为表示边界形态的指标，很少考虑弯道的平面几何形态。而连续急弯在漫滩行洪的过程中，输沙能力发生变化［10］，主要表现为含沙量、输沙率在平滩流量时最大，在流量进一步增大、水流漫滩后逐渐减小［11－12］，其原因在于滩槽水沙交换造成动量、能量损失［13］。因此，本文以非恒定流动床物理模型试验为基础，研究连续急弯的平面几何形态对河段输沙能力的影响，揭示黄河下游连续急弯河段水沙输移的内在规律，以期为黄河下游连续急弯河段水沙灾害防治工程建设与正常运行提供科学合理的依据。

1 试验设置

1.1 研究河段

本文选取黄河下游孙口上下游的连续急弯河段作为研究河段，其上起伟那里断面，下至大田楼断面。研究河段全长约25 km，平均河道纵比降为0.01%～0.015%，主槽平滩河宽400～800 m，均值为650 m，水深3～6 m，均值为4.5 m。研究河段有4个急弯（如图1所示）：C1—C3段包括1＃、2＃两个弯道，C3—C5段包括3＃弯道，C5—C7段包括4＃弯道，中心角θ弧度范围为1.83～2.79（105°～160°），曲率半径与主槽宽度之比rc／B的范围为1.83～2.71。

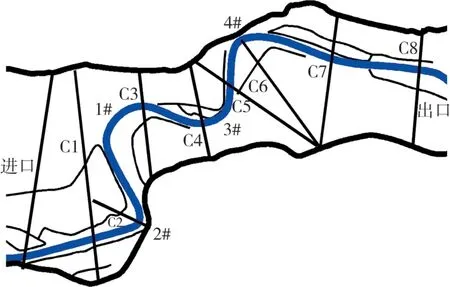
图1 研究河段急弯示意

1.2 模型设计

试验在黄河水利科学研究院试验基地进行。根据试验要求及模型变率限制条件［14］，取模型水平比尺为800，垂直比尺为100，主要相似比尺见表1。模型沙选用d50＝0.04 mm的粉煤灰，悬沙与床沙组成相同，级配如图2所示。模型初始地形采用2021年汛前实测地形资料。试验采用电磁流量计控制进口流量、采用孔口箱控制进口沙量。为实时观测试验中水位、流速、含沙量等的变化过程，沿程共布置8个观测断面，具体位置见图1与表2。

表1 模型相似比尺

图2 模型沙级配

表2 观测断面设置

1.3 试验组次

为探讨非恒定流条件下连续急弯对输沙能力的影响及累积效应，根据历史上黄河下游发生的大洪水，以“82·8”洪水过程及“58·7”洪水过程为基础，设计概化2组模型试验水沙条件，见图3和表3。

表3 模型试验水沙过程

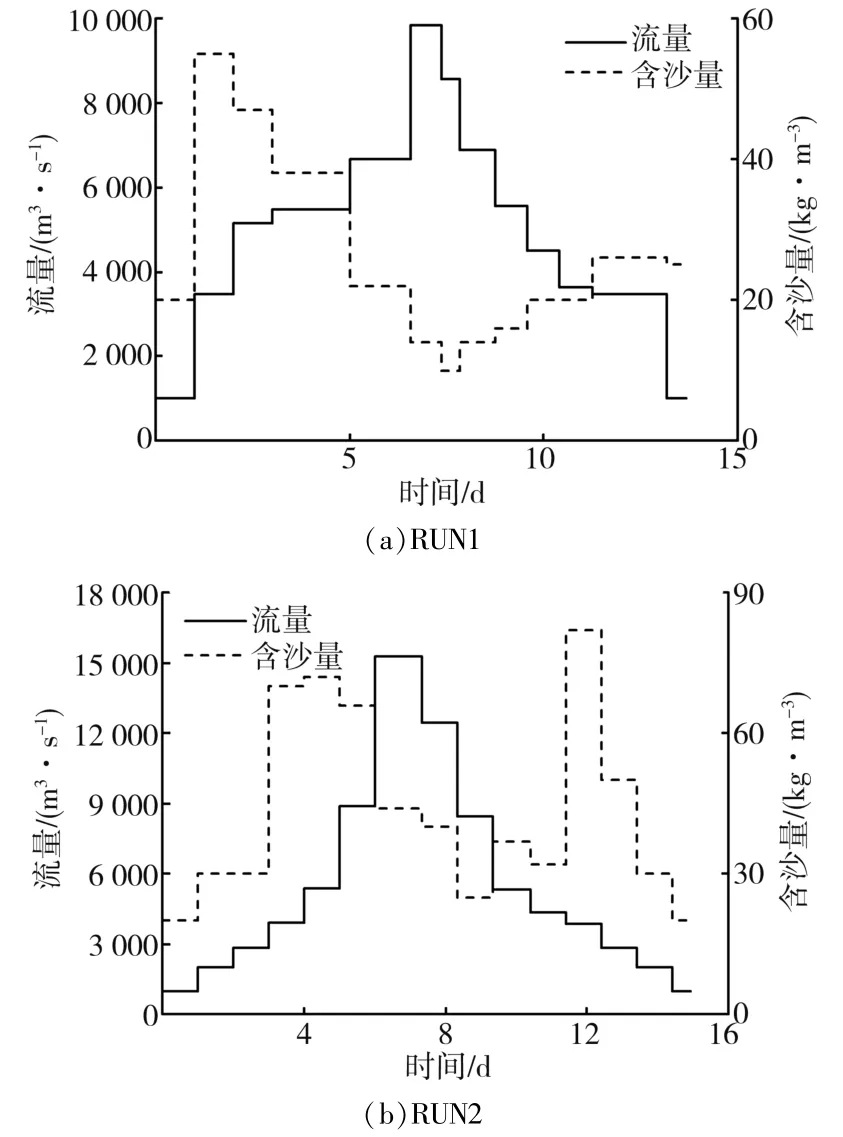
图3 模型试验水沙过程

RUN1工况共有13个流量级（Q＝1 000～9 844 m3／s），含沙量S变化范围为10～55 kg／m3，原型时间13 d 4 h，试验历时4.1 h。RUN2工况共有15个流量级（Q＝1 000～15 285 m3／s），含沙量S变化范围为20～82 kg／m3，原型时间14 d10 h，试验历时4.5 h。试验过程中，当每个流量级水流稳定后，采用测针测量各观测断面的水位，采用旋桨流速仪测量典型断面主槽平均流速，采用比重瓶法测量典型断面主槽内的含沙量。试验结束排干水后，采用水准仪测量各观测断面的床面高程。

2 试验结果

2.1 水位变化

图4为各断面水位变化过程。由图4可以看出，由于两种工况的流量均为单峰过程，因此两种工况各断面水位的变化过程相似，均为先升高后降低。涨水过程中，随着流量的增大，沿程水位逐步抬升，水面比降变化不大；落水过程中，随着流量的减小，沿程水位逐步回落，河段上游部分水位回落幅度较下游部分水位回落幅度明显偏小，水面比降逐步变大。

图4 各断面水位变化过程

2.2 流速变化

图5为典型流量级下断面C1～C7主槽平均流速沿程变化。主槽平均流速与流量成正相关关系，落水阶段主槽平均流速略大于涨水阶段的，这与落水阶段水面比降逐步增大相一致。主槽平均流速总体上沿程逐渐减小，在局部弯道内，流速稍有增大。

图5 典型流量级下断面C1～C7主槽平均流速沿程变化

2.3 断面冲淤变化

图6为RUN2工况各典型断面的床面地形变化。由图6可见，洪水过后，河道断面均出现了不同程度的淤积。大部分淤积发生在滩地以及顺直段的主槽，如图6（a）、（d）、（f）；而弯道段的主槽冲淤变化不大，如图6（b）、（c）、（e）。由此可推断急弯水流的强三维结构虽然能够强化弯道内局地泥沙输移，但弯道河段通过平面上增加河长造成额外的能量损失，从而导致河道整体上呈淤积态势。

图6 典型断面床面地形变化

考虑河道内的机械能变化，单位时间内通过某一断面的水体的机械能可用下式表示：

式中：E为机械能；m为单位时间内通过某一断面的水体质量；g为重力加速度；h为相对水位；v为平均流速。

图7为RUN2工况典型流量级主槽范围内机械能沿程变化。各典型流量级主槽范围内机械能总体上呈沿程递减规律，上游部分（C1—C 3）较下游部分（C3—C 7）的减小幅度明显偏大。值得注意的是，在河段中部（C3—C 4）、中下部（C5—C 6）两处的机械能有局部增大的现象。结合研究河段的平面特征，C1—C3、C3—C5、C5—C7段的弯道段长度占比分别为93%、68%、37%，而C3—C4段以顺直段为主，C5—C6段一半为顺直段，显然急弯段较顺直段造成了河道能量的额外损失。

图7 典型流量级主槽范围内机械能沿程变化

2.4 河道输沙能力

图8为典型断面主槽含沙量变化过程。由图8可知，各典型断面主槽含沙量变化过程与进口含沙量变化过程基本保持一致且沿程递减，可见河道输沙能力沿程总体呈递减趋势。其中，流量上涨阶段，各典型断面主槽含沙量衰减的幅度较大，为26%～46%；流量回落阶段，各典型断面主槽含沙量衰减的幅度较小，为16%～23%。

图8 典型断面主槽含沙量变化

为进一步了解水流过程不同阶段连续急弯对河道输沙能力的影响及累积效应，采用无量纲弧长θrc／B作为弯道段的平面几何特征指标。根据含沙量测量位置可分为3段：C1—C3段包括1＃、2＃两个弯道，C3—C5段包括3＃弯道，C5—C7段包括4＃弯道。表4给出了试验河段4个急弯的平面几何特征，急弯中心角弧度范围为1.83～2.79，曲率半径与主槽宽度之比rc／B的范围为1.83～2.71，无量纲弧长θrc／B的范围为3.35～7.55。图9给出了RUN2工况典型流量级连续急弯平面几何特征无量纲弧长与主槽含沙量衰减率的关系，图中横坐标为累积无量纲弧长，数值越大对应水流经过了越多的弯道。由图9可见，在涨水阶段的各流量级中，每当水流经过一个弯道，含沙量都会有所衰减，且流量越大含沙量衰减率越大，衰减率从9%～28%增大至27%～50%。而在落水初期，流量较大时（大于平滩流量5 398 m3／s）含沙量与涨水阶段的趋势相似；当流量降至平滩流量附近时，含沙量衰减率逐渐减小；当流量降至平滩流量以下时，水流归槽，含沙量衰减率又逐渐增大。说明连续急弯的下游部分淤积量较上游部分淤积量小。

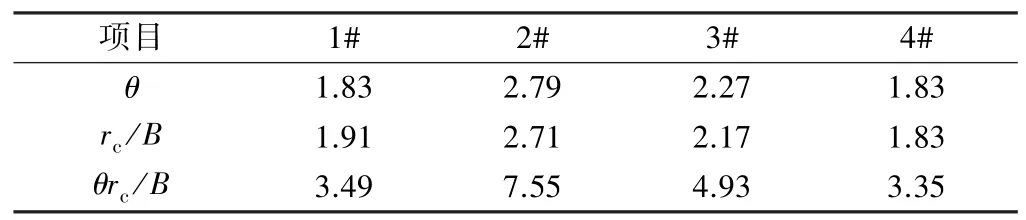
表4 试验河段急弯平面几何特征

图9 连续急弯平面几何特征与主槽含沙量衰减率的关系

3 结 论

通过非恒定流动床概化模型试验，在水位变化、含沙量变化和断面地形变化资料的基础上，探讨了连续急弯对河段输沙能力的累积效应，主要结论如下。

（1）连续急弯造成额外的能量损失，在特定水沙条件下导致河道整体上呈淤积状态。

（2）连续急弯河段输沙能力沿程减弱，整体上呈现出流量越大输沙能力减弱幅度越大的特征。

（3）急弯的平面几何特征可用中心角θ和曲率半径与河宽之比rc／B的乘积θrc／B表示。连续急弯对输沙能力的累积效应在不同阶段有不同的特点，主要表现为涨水阶段弯道平面几何特征θrc／B与输沙能力负相关；退水阶段，当漫滩流量接近平滩流量时，输沙能力在局部弯道稍有恢复，水流归槽后，θrc／B与输沙能力又恢复为负相关关系。