关注知识衔接 让算法可视化

骆虹廷

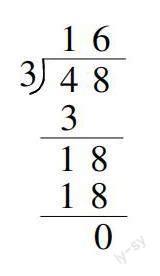
摘   要：为了让学生关注知识衔接，实现算法可视化，以苏教版小学数学三年级上册“除数是一位数的笔算除法”一课为例，在运用迁移中让学生经历分物的过程，在自主探究中让学生经历竖式的记录过程，在巩固练习中让学生经历解决问题的过程。

关键词：小学数学；知识衔接；算理算法；笔算除法

中图分类号：G623.5   文献标识码：A   文章编号：1009-010X（2023）34-0008-03

数学是一门逻辑性极强的理性学科，前后知识之间具有关联性和递进性，让学生在前面已有知识的基础上进行学习。学生在小学阶段接触除法知识有六个阶段：第一阶段是在一年级时，学生学会了用连减的方法计算除法；第二阶段是在二年级时，学生在学习表内乘法后，学会了用乘法口诀解决表内除法；第三阶段是在三年级时，学生学会计算两、三位数除以一位数的笔算除法；第四阶段是在四年级时，学生学会计算两、三位数除以两位数的笔算除法；第五阶段是在五年级时，学生学会计算小数除法；第六阶段是在六年级时，学生学会计算分数除法。整个除法学习的过程中，教师不仅要注重学生理解算理和算法，还要让学生能用除法解决数学问题。

我们在教学苏教版三年级上册第四单元“除数是一位数的笔算除法”一课时，结合唐僧给三个徒弟分桃子的故事，引出48÷3这道除法算式，在分桃子的过程中让学生感受到既可以先分十位上的数也可以先分个位上的数，又让学生体会到除法竖式从高位算起的简便性。

一、运用迁移，经历分物的过程

学生在一年级时就经历了分与合的过程，教师将学生的这种学习经验迁移到本节课的笔算除法课中。课堂伊始，教师出示零散的桃子和排列整齐的桃子，在比较中让学生感受到“分”与“合”的优势，也为学生平均分物埋下伏笔。

（一）体会“分”与“合”

师：（出示桃子）同学们，唐僧要给三个徒弟分桃子，你能一眼看出有多少个桃子吗？为什么我们不能一眼看出桃子的数量？

生：因为桃子这边一个那边一个，太乱了。

师：你有什么办法让别人一眼就看出桃子有多少个？

生：我们可以10个10个地放在一起，这样数只要看一看有几个十和几个一。

师：（4个篮子，每个篮子有10个桃子；零散的桃子有8个）现在我们就能马上说出一共有多少个桃子了？（48个）人类为了一眼就能看出数量多的物体到底有多少，可以进行分组，再合起来就方便多了。

（二）经历两种分物的过程

师：同学们，唐僧要把48个桃子平均分给3个徒弟，如果你是唐僧，你会先分哪部分桃子？

（有的学生说“先分零散的8个桃子”，也有的学生说“先分篮子里的桃子”。）

师：那到底先分哪部分桃子呢？我们来听听第一个徒弟怎么说吧！（播放：我想先分篮子里的桃子）同学们，这个徒弟想先分篮子里的桃子，想一想你会怎么分？

生：我会先把4个篮子里的桃子平均分成3份，每个徒弟可以分到1个篮子，还剩1个篮子的桃子。接着我们把这个篮子的10个桃子倒出来，和零散的8个桃子合起来再平均分成3份，每个徒弟可以拿到6个桃子。所以每个徒弟可以分到1个篮子的桃子和零散的6个桃子，他们能分到16个桃子。

师：我们还看到第二个徒弟也有话说，你猜他会说什么？

生：我猜他想先分零散的8个桃子。

师：（播放：我想先分散的8个桃子）果然和我们同学想得一样，如果你是第二个徒弟，你会怎么分？

生：我会先把分散的8个平均分成3份，每份有2个桃子，还多2个；现在零散的桃子不够分了，我再把4个篮子平均分成3份，每份有1个篮子，还多出1个篮子。然后我把1个篮子的10个桃子倒出来，和分散的2个桃子合在一起是12个桃子再平均分成3份，每份有4个。最后每份分到2个桃子、1个篮子的桃子和4个桃子，一共有16个桃子。

在这个教学片段中，学生在实际分物过程中想到先分零散的桃子和先分整篮桃子这两种情况，再体会分桃子过程中是如何分与如何合，关键是要知道在什么时候进行分与合、为什么要这样分与合，为下一个环节中用竖式记录分物过程做好准备。

二、自主探究，经历竖式的记录过程

竖式的记录过程是一种数学计算方法，用于解决多位数加法、减法、乘法和除法等计算问题。它的作用在于提供一種清晰、有序的方式来展示计算的每个步骤，使得计算过程更易于理解、检查和纠正错误。学生结合上一个环节中的两种分物过程，用除法竖式记录下来，比较体会到从十位算起的简便性。

师：我们看到了两种不同的分物方法，你能把这两种分物过程用竖式记录下来吗？谁来说一说你的竖式是怎么写的？

生1：我写好除法竖式，我先试了从个位算起，发现从个位开始算是不行的。我就开始先算十位，用4除以3，商是1个十，就在十位上写1，4个十减去3个十还有1个十，再把个位上的8抄下来，这样就用18除以3，商是6。所以48÷3=16。

师：4在十位上，我们是用4个十除以3得到1个十还多1个十，就在十位上商1，再把余下的1个十和个位上的8组合在一起就是18，18个一除以3得到3个一，就在个位上商6。这位同学说从个位开始不行，但是刚才我们分桃子也是可以从个位开始先分的，有同学写出从个位先算的竖式吗？

生2：我是从个位开始算的，8除以3等于2余2，就在个位上商2；2不能再被3分了，就先分十位上的4，4个十平均分成3份，商是1个十余1个十，就在商的位置写10；现在还剩下1个十和2，组合在一起是12，12个一除以3的商是4。最后把三个商2、10和4加起来，所以48除以3的商是16。

师：这位同学从个位算起，把商分成了三部分，你能看懂吗？分别是怎么来的？

生3：能。先算8除以3，再算4个十除以3，最后算12除以3。

师：同学们，请你结合分物过程和竖式过程，比较从十位算起和从个位算起这两种方法，它们有什么相同点和不同点？

生：相同点是都在计算同一道除法竖式，结果是相同的；在计算过程中都会有分与合。不同点是从十位算起只要两步，而从个位算起有三步。

在这个教学过程中，竖式的记录过程是學生结合分物过程对除法的抽象，用简洁易懂的方法记录每一步分物过程，让学生经历从具体到抽象的整个过程，升华对除法竖式的理解。同时，教师引导学生比较从个位算起和从十位算起这两种方法的异同点，进一步优化除法竖式的算法，总结出除法竖式的一般算法：从高位除起，先看最高位。最高位够除，除到哪一位，商就写在哪一位上。如果最高位不够除，就看前两位，除到哪一位，商就写在哪一位上。

三、巩固练习，经历解决问题的过程

当学生掌握了两位数除以一位数的笔算除法后，教师在巩固练习中设计了三位数除以一位数的笔算除法，让学生在竖式计算中实现算理和算法的迁移，进一步体会到从高位算起的优越性。同时，教师融入了估算，一方面可以提高学生的估算能力，另一方面也有助于学生检验竖式计算结果是否正确。

师：同学们，在四川汶川地震的时候，中国各个省都团结一心，互帮互助。有一支5人组成的救援队，带着救援物资和药品共576斤。你能提出什么数学问题？

生：平均每人要带多少斤？

师：请你估计平均每人大约多少斤？

生：如果把576斤估成500斤，每人至少要带100斤；如果把576斤估成600斤，每人大约要带120斤。

师：同学们，每人到底多少斤？请你先列式，再用竖式解决这个问题。

生：576÷5，先算5个百除以5，在百位上商1；把十位上的7抄下来，7个十除以5，在十位上商1，还多2个十；这2个十和个位上的6合起来是26，26除以5，在个位上商5，余1。

师：我们用除法竖式计算出了576÷5=115（斤）……1（斤），平均每人要带115斤的物体，你有什么想说的？

生：115斤相当于一个成年人的体重了，救援人员要背一个成人了，太辛苦了。

师：是的，这就是中国人团结一致的体现。刚才老师发现有的同学还继续往下分，算出了115.2斤，我们在后续的课中继续研究。

在这个教学过程中，教师在巩固练习中融入爱国主义教育的素材，不仅让学生经历了三位数除以一位数的笔算除法过程，还让学生体会到救援人员的大爱无私的奉献精神。同时，还有的学生并不满足于除法竖式计算，不仅将分与合的学习经验迁移到解释算理和算法上，还将不断细化计数单位的经验迁移过来，从“1”中细分10个“0.1”再进行计算，由整数除法竖式延伸到小数除法竖式。

总之，这节课中教师由学生对分与合的已有经验入手，先带领学生探索了唐僧分东西过程，引出先分篮子里的桃子和先分零散的桃子这两种分法；再引导学生用除法竖式记录分桃子的过程，将除法竖式与分桃子的过程对应起来，在“边分边除”中理解除法的算理和算法，同时在比较两种除法竖式中优化出最佳算法。最后让学生自己探究三位数除以一位数的笔算除法，实现了除法竖式计算方法和计算过程的迁移，有利于学生体会除法竖式算理和算法的一体化，实现运算的一致性。

参考文献：

［1］宋晓光.小学数学计算教学中算理和算法的有效融合——以苏教版“小数加法和减法”为例［J］.名师在线，2022，（35）：55～57.

［2］陈   梅.小学低年级数学“算法多样化”的教学思考［J］.求知导刊，2020，（10）：36+38.

［3］赵春霞.关于小学数学算法多样化的认识与思考［J］.教育实践与研究（A），2013，（05）：70～72.