基于多步长的多机器人分布式巡逻算法研究*

白耀文，杜亚江，李宗刚

(1.兰州交通大学机电工程学院，甘肃 兰州 730070；2.兰州交通大学机器人研究所，甘肃 兰州 730070)

1 引言

多机器人巡逻是指为了保护或监控指定区域，多个机器人频繁前往或通过该区域的行为，广泛应用于环境监控、信息收集、入侵监测及其他安全领域。多机器人巡逻策略主要有2种：集中式巡逻策略和分布式巡逻策略。2种巡逻策略都广泛应用于安防和服务等领域。目前多机器人巡逻研究主要集中在分布式巡逻策略，其巡逻性能主要由节点访问频率和空闲时间来衡量[1]。

在多机器人巡逻策略研究初期，研究方向主要集中在对集中式巡逻策略的研究，即多个机器人收集环境信息并将其传递给中央机器人，中央机器人通过一定的数据处理后指导机器人运动。Machado等人[2]提出了认知协同策略，核心为在巡逻过程中上位机知道所有节点的信息，其选择共享空闲值最大的节点，使其成为机器人的下一个目标节点，同时避免将同一个节点分配给多个机器人,然后利用寻路技术，机器人可以实现从当前位置到目标节点的自主移动。

随着多机器人巡逻策略研究的深入，研究人员发现传统的集中式巡逻算法在面对复杂多变的环境时具有较大的局限性。当环境信息发生变化或者中央机器人受到入侵时[3]，集中式巡逻算法无法及时进行策略调整，难以完成巡逻任务。Portugal等人[4]提出了基于贝叶斯决策的分布式多机器人巡逻算法，该算法基于贝叶斯数学模型，通过建立奖励函数和效用函数来对机器人的下一个目标兴趣点进行选择。由于该算法具有较强的灵活性，它可以很好地解决传统预先定义巡逻算法中其确定性本质带来的潜在可入侵危险。在此基础上，Portugal等人[5]针对分布式多机器人巡逻中的容错性和可拓展性提出了2种算法，即贪婪贝叶斯策略GBS(Greedy Bayesian strategy)和状态交换贝叶斯策略SEBS(State Exchange Bayesian Strategy)。贪婪贝叶斯策略的思想是机器人按照自己的决策并结合效用函数，在每个阶段找到局部最优选择，进而完成指定区域的巡逻任务。SEBS是GBS的延伸，在GBS的基础上引入了概率质量函数(1/2几何序列)，将机器人数量这一因素加入到机器人的决策过程中，在一定程度上减少了机器人之间的冲突，因而在性能上优于GBS。但是，当环境信息或机器人数量发生变化时，这2种算法的性能会受到很大的影响。因此，Portugal等人[6]在GBS的基础上提出了并行贝叶斯策略CBLS(Concurrent Bayesian Learning Strategy)算法,该算法考虑了不同先验概率的情况，并在决策过程中引入了机器人第2步前视顶点的空闲时间，结合自适应学习来灵活调整机器人决策，使各个机器人可以很好适应复杂多变的环境。Farinelli等人[7]提出了2种动态任务分配方法：贪婪的基线方法DTA-G(Dynamic Task Assignment-Greedy)和以市场为基础的基于连续单物品拍卖的方法DTAP(Dynamic Task Assignment Patrolling)。DTAG将地图节点的瞬时空闲时间引入到决策过程中，通过效用函数指导机器人运动，且每次决策只给每个机器人指定一个巡逻节点。而DTAP通过给每个机器人指定一个巡逻节点集，来避免机器人巡逻路径的交叉，减少多机器人间的相互干扰，进而提高巡逻效率。实验结果表明，DTAP在多连通地图中的巡逻性能优于DTAG的。赵云涛等人[8]提出了一种基于平均最大空闲时间EGMI(Estimated Global Maximum Idleness)的巡逻算法,该算法将巡逻地图的全局平均最大空闲时间引入到决策过程中，根据最大空闲时间的大小估算在特定巡逻环境中完成巡逻任务所需要的机器人数量，进而得知完成巡逻所需的最优机器人数量。EGMI算法在机器人数量优化上有着很好的应用，但当机器人巡逻数量发生变化时，其巡逻效果可能会受到较大影响。

综上所述，在复杂多变的巡逻环境中，上述巡逻算法并不总是能达到巡逻效果最优。本文在全局平均空闲时间的基础上，提出了基于多步长的分布式巡逻算法MSLA(Multi-Step Length Algorithm)，通过考虑机器人前视节点，即目标节点邻居的平均空闲时间和节点个数来缩短巡逻系统的全局平均空闲时间，使其更能适用于机器人数量较多时的巡逻情况，最终达到改善巡逻效果的目的。

2 问题描述

在给定环境中通过一组数量为m的机器人R=(R1,R2,…，Rm)进行巡逻，每个机器人都已知所要巡逻环境中的巡逻节点，则可以得到机器人的无向导航图G=(V,E)，使得机器人可以评估巡逻环境的拓扑结构。V0和Vi为地图上的巡逻节点，所有节点构成集合V，记为V={V0,…,Vi,Vj,…,Vn}，E表示相邻节点连接形成的边集合，表示各个节点的连通性，这些边可提供机器人通行且互不相交，其中将某一节点相邻的邻居节点称为该节点的前视节点。节点V0和Vi间的路径长度记为l0,i，节点的重要度分别记为e0和ei。

为了评价不同算法的性能，引入一个合适的评判标准是非常重要的。传统的评价标准主要有：空闲时间[9]、访问频率[10]和机器人运动的距离等。本文引入节点空闲时间，即节点被连续访问的时间间隔，通过将目标节点和前视节点的平均空闲时间引入到效用函数中来提高机器人决策的合理性。规定机器人通信半径有限，不能进行通信全覆盖，只能与相邻的个别机器人进行双向通信[11]。图1和图2是以自建地图Lab为例的路径拓扑图和通信拓扑图。为简化起见，图中巡逻节点Vi均简记为i，后文各图也按照类似方法处理，不再另作说明。

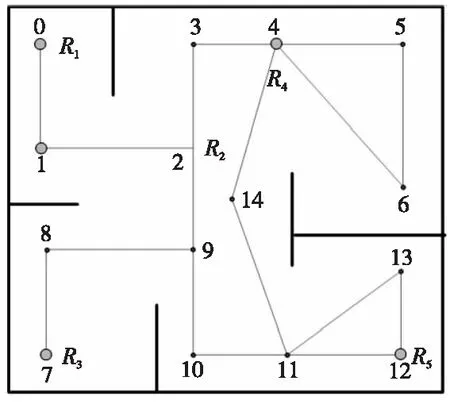
Figure 1 Lab path topology图1 Lab路径拓扑图

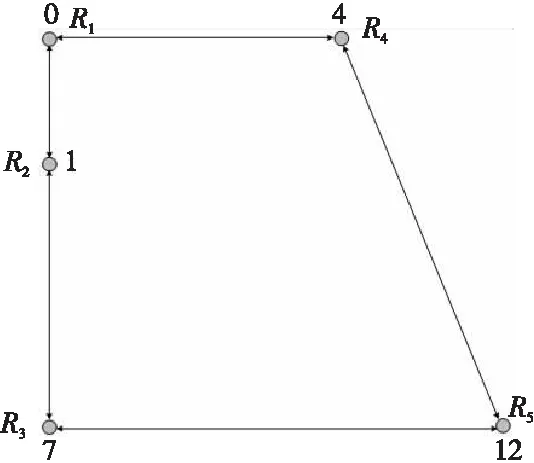
Figure 2 Lab communication topology图2 Lab通信拓扑图

在行为决策阶段，每个机器人与自己相邻最近的伙伴进行双向通信，如图2所示。输入为当前的本地信息，输出为机器人的行为策略，所巡逻环境的信息和机器人的决策算法直接影响着多机器人的巡逻效果。为了评价巡逻算法的性能，本文将全局平均空闲时间作为评判标准引入到算法决策过程中。

记机器人当前所在节点为V0点，机器人R1第k次访问节点Vi的空闲时间如式(1)所示：

IVi(tk)=tk-tk-1

(1)

其中，tk表示机器人R1在第k次访问节点Vi的时刻，所得到的空闲时间可以储存在该机器人中，故得到节点Vi在当前时刻的平均空闲时间如式(2)所示:

(2)

(3)

其中,n表示巡逻区域中的节点总数。全局平均空闲时间越短，说明每个节点的安全度越高，即巡逻效率越好。

3 基于多步长的分布式巡逻算法

为了提高多机器人巡逻过程中的效率，本文提出了一种基于节点平均空闲时间的多步长分布式巡逻算法。其决策过程如下：当机器人R1处在节点V0时，通过信息交互采集环境信息及其他机器人所传递的信息，对该数据进行处理，通过特定的效用函数来指导该机器人运动到相应目标点。

假设机器人R1处在V0节点上，则其到达下一个相邻节点Vi的时间可表示为式(4)：

(4)

其中，l0,i为节点V0到节点Vi的路径长度，c为巡逻机器人的速度，这里规定每个机器人速度相同。在多机器人巡逻过程中节点重要度集合为e={e0,e1,…，en}。巡逻节点的重要度通常是由人们的先验经验和巡逻场所已有的巡逻数据相结合来确定的，因此巡逻节点重要度的大小设置具有很大的不确定性。但总体而言，当目标节点在巡逻场所中越重要或该目标节点发生盗窃、安全事故等情况的概率越高，则该巡逻节点的重要度就越大。在本文中，假设每个节点的重要度恒定不变，则机器人从节点V0到节点Vi的弧强度θ0,i如式(5)所示：

(5)

注意，θ0,i≠θi,0。则机器人第1步的效用函数为：

(6)

若机器人只考虑第1步目标节点，可能会导致机器人运动的不均匀和相互干扰，进而影响巡逻效率，故本文引入第2步节点集，即前视节点集。将节点V0在Vi方向上的前视节点集记为VNG,i={Vh,Vj,…，Vp}，则其相对应的前视节点集的平均空闲时间如式(7)所示：

(7)

其中，z为节点V0在Vi方向上前视节点的数量。则V0节点相应的第2步效用函数如式(8)所示：

(8)

(9)

(10)

其中,β表示前视节点数量与其中机器人数量的比值；φ为当前节点V0在Vi方向上前视节点中的机器人数量；ω为第1步效用函数在整体效用函数中所占的权重，该参数可以根据巡逻地图中节点的分布情况进行适当调节，但总体来说该参数设置要大于0.5。因为相邻节点的环境信息总是可靠和最新的，而当机器人到达目标节点时，前视节点集中的环境节点信息可能会发生改变。

如果有2个及2个以上的机器人与目标节点Vi相邻，则在当前tk时刻节点Vi的效用函数为:

(11)

式(11)中，当节点V0的前视节点上有1个或多个机器人时，机器人在寻找目标点Vi时要考虑前视节点数量与其中机器人数量的比值β。β越小，说明该前视节点集中机器人的密度越大，可以很好地巡逻该区域，因而机器人R1在进行决策时对前视节点考虑越少。

如果只有1个机器人去竞逐节点Vi，则在当前tk时刻节点Vi的效用函数为：

(12)

式(12)表示当节点V0的前视节点中没有机器人时，机器人R1在选择目标节点时对前视节点考虑较多。只有2步节点相结合才能缩短节点的全局平均空闲时间，进而改善机器人的巡逻效果。

通过式(11)和式(12)可以计算出在上述2种情况下目标节点的效用函数，机器人可通过效用函数的大小来对目标节点进行选择。目标节点的效用函数值越大，表明该目标节点越需要机器人去访问。机器人通过效用函数来选取合适的目标节点，可以减少机器人数量较多时所产生的相互干扰，进而缩短巡逻区域的全局平均空闲时间，最终达到提高巡逻效率的目的。

在此将执行巡逻任务的算法简称为MSLA,其伪代码如算法1所示。

算法1基于多步长的分布式巡逻算法

1 Initialization;

2whiletruedo

3forallVi∈Vdo

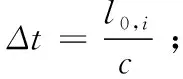
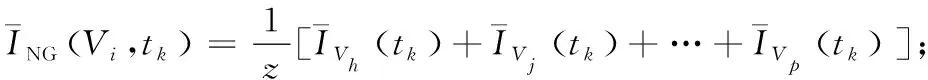
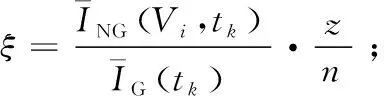
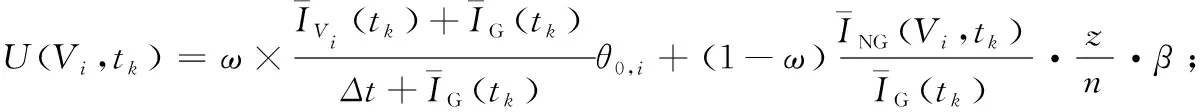
9ifφ=0then

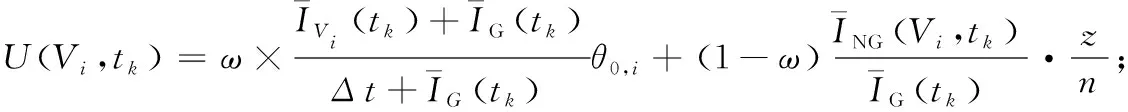
11else

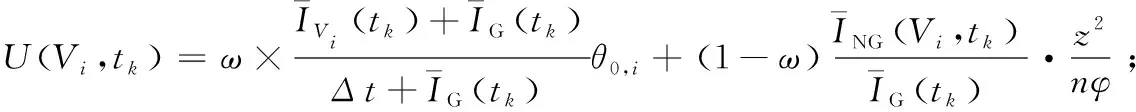
13endif

14Vi←argmax(U(Vi,tk))；

15endfor

16 publish intention messageVi；

17 move to vertexVi;

18whileone of robot reachedVido

19 publish message to the other robots as arrivingVi；

20 update idleness (V)；

21endwhile

22Vi←Vi+1;

23endwhile

24end

在巡逻过程中，机器人通过信息交互来收集巡逻节点的环境信息，并计算出各个节点的空闲时间，进而得到当前时刻节点的平均空闲时间，然后将节点平均空闲时间引入到效用函数中，结合节点数量和节点重要度计算出每个环境巡逻节点的效用函数，最后比较机器人相邻节点的各个效用函数大小。若某一相邻节点的效用函数最大，说明该目标节点最需要机器人去访问，则机器人根据结果指导自己向该点移动。当机器人到达目标节点后，该机器人将到达信息发送给其他机器人(对应算法第19行)，而后更新当前巡逻节点信息(对应算法第20行)，多种信息依次传递给各个机器人，多机器人会根据所收集的环境信息独立决策，进而完成巡逻任务。

4 仿真实验

为了验证本文所提巡逻算法的有效性，在ROS(Robot Operating System)环境下搭建多机器人巡逻仿真平台multi_robot_patrol来对算法性能进行测试，而后通过和现有算法进行对比来分析本文算法的优劣性。在仿真过程中，机器人在二维地图的基础上使用ROS导航和定位系统，并结合算法完成机器人路径自主规划，同时避免多个机器人在移动中发生碰撞。

仿真使用了Example和Grid 2种二维仿真地图来验证算法的可行性，其环境拓扑图如图3所示。

Figure 3 Topology of simulation experiment environment图3 仿真实验环境拓扑图

表1为2种仿真地图拓扑图信息。当采用数量为4，8，12的Turtlebot3机器人时，在上述2种仿真地图上进行算法验证，仿真通过multi_robot_patrol仿真平台进行实验，同时进行数据记录。仿真中，多机器人移动速度均为1 m/s，每组仿真实验持续半小时。

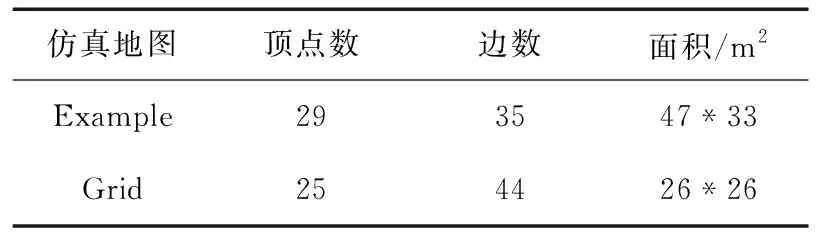
Table 1 Topological information of simulation maps表1 仿真图拓扑信息

Table 2 Simulation results in Example map表2 在Example仿真地图中的仿真结果 s

Table 3 Simulation results in Grid map表3 在Grid仿真地图中的仿真结果 s

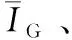
本文分别选取机器人数量为4,8,12的巡逻结果进行数据分析。图4通过绘制箱线图分别对机器人不同数量和不同环境中的节点空闲时间进行了统计分析。在该实验中，箱线图中所绘制的矩形框表示空闲时间的集中区域，矩形框越小，表明使用该算法所得到的节点空闲时间越集中，图中上下2条短黑线分别表示非异常空闲时间的最大值和最小值，而矩形框中的长实线表示节点空闲时间的中值,可以看出空闲时间的离散程度，黑色小圈表示空闲时间的异常值。

由图4可知，当机器人数量为4时，各算法的节点空闲时间较为分散，且全局平均空闲时间较长，随着机器人数量的增加，各算法的空闲时间慢慢收敛，全局平均空闲时间也逐渐缩短。当机器人数量为8时，在Example和Grid仿真地图中，相较于其他几种算法，MSLA的矩形框较低，且矩形框较小，说明该算法在机器人数量为8时具有较短的空闲时间和较好的收敛性，因而更加高效，更加稳定。当机器人数量继续增加时，从箱线图中可以看出，MSLA相较于其他几种算法同样保持着较短的空闲时间和较好的收敛性，因此可以看出在同一环境中巡逻时，当机器人数量较多时，MSLA的巡逻效果优于其他几种算法的。

Figure 5 Convergence of for five algorithms in Grid map 图5 5种算法在Grid仿真地图中的和收敛性

为了分析MSLA随着机器人数量的增加巡逻性能的变化情况，本文在Example和Grid仿真地图中，通过仿真平台对机器人数量进行改变来对巡逻效果进行分析，分析结果如图6所示。

Figure 6 Patrol effect of five algorithms with different robot numbers图6 5种算法在机器人数量不同时的巡逻效果

由图6可知，随着机器人数量的增加，各巡逻算法的全局平均空闲时间逐渐缩短，表示巡逻性能逐渐提高，但随着机器人数量的逐渐饱和，其机器人之间的干扰逐渐增大，影响了算法的巡逻性能，反而会导致巡逻性能降低。从全局平均空闲时间曲线趋势可以看出，相较于其他算法，MSLA的全局平局空闲时间曲线在机器人数量较多时仍然可以保持在较小的数值范围内，表明该算法在机器人数量较多时其巡逻性能优于其他算法的。以图6a为例，当机器人数量达到8后，随着机器人数量的增加，MSLA的全局平均空闲时间仍保持在较小的数值范围内，且没有随机器人干扰的增加出现上升趋势，反观其他几种算法，在机器人数量达到8后全局平均空闲时间有上升趋势，且整体大于MSLA的平均空闲时间。在图6b中，虽然MSLA的全局平均空闲时间曲线也存在一些波动，但相较于其他算法的曲线趋势，MSLA的整体全局平均空闲时间仍保持在较小数值水平，且在机器人数量为12时，有着最短的全局平均空闲时间，此时多机器人系统巡逻性能较好。

5 结束语

本文针对多机器人巡逻问题，提出了一种基于多步长的多机器人分布式巡逻算法MSLA，通过将多步长巡逻节点信息引入到机器人决策过程中，从而缩短节点全局平均空闲时间。在ROS环境下的实验结果表明，该算法在机器人数量较少时没有明显的团队优势，但随着机器人数量增加，该算法在巡逻过程中所表现出来的优势越来越明显。当机器人数量较多时，从实验结果可以看出，MSLA所得到的全局平均空闲时间和全局空闲时间标准差都较小，说明该算法在完成巡逻任务的同时，具有较好的巡逻效率和稳定性。在后期工作中，将尝试考虑多机器人巡逻过程中通信延迟对巡逻效果的影响，进而对本文所提算法进行进一步完善。