Flink水位线动态调整策略*

吕鹤轩,黄 山,艾力卡木·再比布拉,吴思衡,段晓东

(1.大连民族大学计算机科学与工程学院，辽宁 大连 116600；2.大数据应用技术国家民委重点实验室，辽宁 大连 116600； 3.大连市民族文化数字技术重点实验室，辽宁 大连 116600)

1 引言

近年来随着信息技术的发展，各类门户网站﹑搜索引擎和社交媒体软件等产生的数据不断膨胀，由互联网数据中心IDC(Internet Data Center)发布的白皮书《数字化世界——从边缘到核心》预测：到2025年，全球的数据量将增至175 ZB[1]。

大数据中有着非常丰富的数据信息，并且这些信息蕴含着很高的分析和使用价值，这也就提高了对数据挖掘实时性和准确性的需求。随着大数据时代的到来，传统的单机处理框架无法满足在巨大数据量的情况下的计算需求，分布式大数据处理框架应运而生。首先由谷歌提出的MapReduce[2]编程模型，到第1代大数据框架Hadoop[3]的诞生，到由内存计算的批处理框架Spark[4]，再到现在具有高吞吐、低延迟等特性的流处理框架Flink[5]。大数据计算框架随着大数据计算需求的提高不断地发展。

衡量大数据的数据挖掘性能有2个最重要的任务指标：一是实时性，如海量的数据规模需要实时分析并迅速反馈结果；二是准确性，需要从海量的数据中精准地提取出隐含在其中的用户需要的有价值的信息。数据流的事件时间是数据流中事件实际发生的时间，他以附加在数据流中事件的时间戳为依据。事件时间将处理速度和结果彻底解耦，无论数据流的处理速度如何、事件时间到达算子的顺序怎么样，基于事件时间的窗口都会生成同样的结果。

数据挖掘过程中通常需要窗口根据事件时间进行聚合计算，而数据从产生到流入Kafka[6]消息队列再经过分布式处理框架数据源流入分布式处理框架进行计算，往往因网络传输速度不同、分布式节点计算性能不同等原因，导致数据流入算子的先后顺序和数据事件时间存在着局部的乱序或者数据延迟现象。为解决此问题，Flink提出了水位线机制。水位线是一个全局事件进度指标，通过设置最大允许乱序时间表示系统确信不会再有延迟事件到来的某个时间。窗口由事件的事件时间戳触发开启，窗口关闭和触发计算则是通过水位线机制来主导。但是，水位线最大允乱序时间，也就是容错值的大小，使计算必须在实时性和准确性之间进行取舍。水位线设置过小会导致大部分数据因为迟到无法参与窗口计算，大大降低计算的准确性；水位线设置过大时，虽然保证了大部分数据都能参与计算，但是为等待太多严重迟到的无价值数据会导致窗口计算触发延迟，过长的等待时间大大降低了计算的实时性。综上所述，在基于事件时间窗口的分布式计算中如何用更低的时延产生更少的迟到数据，使作业的窗口计算同时兼顾作业的准确性和实时性，是一个急需解决的问题。

在不确定弹性数据流乱序程度的情况下，传统的水位线设置效率低下，无法保证计算的实时性和准确性。针对该问题，在不确定乱序程度的弹性流数据情况下，本文提出基于事件时间窗口的水位线动态调整策略。该策略在不确定乱序程度的弹性流数据情况下，可以在保证大部分有价值数据计算准确性的同时，有效提高计算的实时性。

本文的主要工作包括3个方面：

(1)提出了一种基于事件时间窗口的流数据微簇模型。该模型将事件时间的流数据按到达算子的顺序分为微簇，此微簇的事件时间乱序程度代表当前时刻局部数据流的事件时间乱序程度。

(2)提出了基于局部事件时间乱序度的水位线动态调整策略。该策略根据局部数据的事件时间戳乱序程度动态调整水位线大小，即允许最大乱序时间的大小。

(3)在Apache Flink框架上的对水位线动态调整策略进行实验。实验结果表明，相比传统水位线机制，水位线动态调整策略可以有效提高窗口计算的性能比。

2 相关工作

在现实世界中，基于事件时间的流处理系统因为网络带宽不同、节点性能不同等原因存在不确定弹性乱序问题，现有的水位线机制无法在保证计算的准确性的同时保证计算的实时性。图1所示为数据流在数据流时间模型的生命周期。

Figure 1 Life cycle of stream data 图1 流数据生命周期

Shukla 等人[7]针对数据流不同的操作时间类型和统计的窗口技术进行讨论。Li等人[8]针对流数据乱序问题提出了一种新的核心流代数操作的物理实现策略，包括基于堆栈的数据结构和相关的清除算法，采用物理的形式一定程度解决了数据流乱序问题，实验结果表明，物理策略可以有效解决流数据乱序问题。Bhatt等人[9]设计了一个可以处理流数据延迟的流处理模型，并提供了一个端到端的低延迟系统，通过实验表明，当窗口大小等于数据到达率时，系统延迟可以有效减少。Affetti 等人[10]针对流处理的实时性以及窗口和时间的概念提出了Dataflow Model模型。Akidau等人[11]提出了针对时间语义进行详细检测的数据流模型，解决了流数据无界和乱序的问题。Bhatt等人[12]通过分析水印和触发方法来解决无界数据中的乱序和其他非常规问题。Bhatt等人[13]提出了在大数据处理中使用适当的管道和水印来处理延迟和吞吐量的方法。高自娟等人[14]提出了一种基于变尺度滑动窗口的流数据聚类算法。该算法采用动态变化的滑动窗口来采集流数据，利用带有平均时间戳与平均权值的混合指数直方图来支持数据处理，从而能更好地捕获动态变化的流数据。徐江等人[15]结合基于分区与基于时间2种滑动窗口思想，构建单位时间周期下融合子流处理结果的滑动窗口模型，采取并行实时运算模式实现了实时流数据处理。

针对处理不确定弹性流数据乱序问题，虽然前人已经做了相应的研究并且获得了一定的效果，但针对不确定乱序程度或弹性乱序流数据情况下的计算优化研究仍有很大空间。

3 相关概念介绍

3.1 Flink框架

Flink是第3代流处理引擎，它支持精确的流处理，同时能满足各种规模下对高吞吐和低延迟的要求。Flink对底层的操作进行了封装，从而为用户提供了流处理Datastream API和批处理DataSet API 2个接口。用户使用这些接口就可以完成基本的流数据处理任务和批数据处理任务。

3.2 Flink的流处理

3.2.1 Flink的时间语义

时间语义是Flink的四大基石之一。在Flink的流处理中会涉及到不同的时间概念，根据用户不同事件类型需求，Flink的时间主要分为事件时间、进入时间和处理时间3类。事件时间是指事件创建的时间，它通常由事件所携带的时间戳表示，例如事件的生成时间。进入时间是指数据流入Flink处理框架的时间。处理时间是指数据流入Flink框架后本节点对本条数据进行计算操作的本地时间。

以上3种时间语义中，因为事件时间将计算速度和计算结果内容彻底解耦，无论数据流的处理速度如何、事件时间到达算子的顺序怎么样，基于事件时间的窗口都会生成同样的结果，而且事件时间相对其他2种时间更具有研究价值，所以大多数流处理任务都会选择使用数据的事件时间语义。

3.2.2 Flink的窗口分类

对于流处理系统而言，流入的消息不存在上限，处理的流数据可能是一个持续到达且无穷的事件流。所以，对于聚合操作和连接操作而言，流处理操作需要对流入的消息进行分段处理，然后基于分段后的每一段消息进行聚合计算或者连接等操作。此时的分段和分端口计算操作即为窗口。窗口是流式处理计算中一类十分常见的操作。Flink窗口操作主要分为滚动窗口、滑动窗口、会话窗口和全局窗口4类。滚动窗口将无限的数据流按固定大小拆分成不同的窗口，不同的窗口之间的事件数据没有交叉重叠。滑动窗口有2个参数，分别是窗口大小和滑动大小，不同窗口之间可以有事件数据交叉重叠。会话窗口用一个固定的时间间隔阈值来划分不同的窗口。全局窗口把所有相同键值放入同一个窗口，全局窗口没有起止的时间,需要自定义触发计算，否则窗口永远不会进行聚合计算。

3.2.3 基于事件时间的水位线

在使用事件时间处理流数据的时候会遇到数据乱序的问题，流处理从事件产生、流经Source、再到操作算子需要一定的时间。理论情况下，传输到操作算子的数据都是按照事件时间产生时的时间顺序而来的，但是分布式环境下会因为网络延迟、计算节点性能不同和数据背压等原因而导致乱序的产生，特别是使用分布式消息队列系统时，因此，大部分情况下多个分区之间的数据无法保证有序进入窗口计算。图2为数据流在系统中的理想顺序和真实顺序。但是，在进行窗口计算的时候，不能无限期地等下去，必须要有一个机制来保证在特定的时间后触发窗口计算。

Figure 2 Diagram of flow data out of order图2 流数据乱序情况图

水位线是一个进度指标，本质上也是一种时间戳，根据水位线的插入类型分为有序水位线、无序水位线和多并行水位线。水位线表示系统确信不会再有延迟事件到来的某个时间点。水位线的工作原理是向数据流中插入当前最大事件时间戳减去最大等待时间的时间戳，此时间戳即为水位线，计算窗口通过处理后的水位线来决定是否触发窗口计算。等待时间也称为容错值，即水位线的大小。例如，当一个窗口算子接收到T的水位线，就可以认为不会再有任何时间戳小于T的事件到来了。本质上，水位线提供了一个逻辑时钟，用来告知窗口当前的事件时间，以及代替原来的数据事件时间触发窗口关闭计算，但是窗口的开启还是由数据的事件时间来触发。图3为水位线工作原理图，系统按照规则向流数据中插入代表水位线的时间戳，当水位线大小设为0 s时，水位线时间戳会紧挨着插入流数据，当水位线大小设为2 s时，水位线时间戳会在数据到达后等待2 s然后插入流数据中。

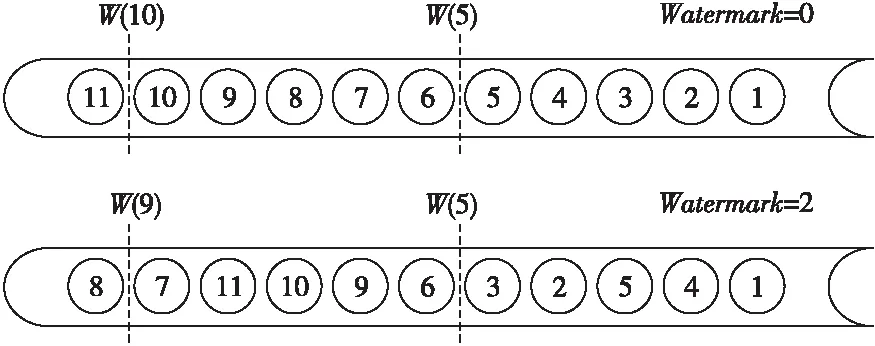
Figure 3 Principle of watermark图3 水位线工作原理

水位线可用于平衡延迟和结果的完整性。较小的水位线保证了低延迟，但随之而来的是低准确性。该情况下，会有大部分有价值数据因为迟到无法参与窗口计算。反之，如果水位线过大，虽然可信度得以保证，但可能会无谓地增加处理延迟。当前的水位线虽然维持了低延迟和高准确率的平衡，但是系统在面对未知乱序程度的数据流或者弹性乱序的数据流时无法做出弹性应对。水位线只允许在结果的准确性和延迟之间做出取舍，现有的方法并不能二者兼得。

4 基于事件时间窗口的动态水位线

本节先对传统水位线机制进行简单分析，然后对基于事件时间窗口的流数据处理建立模型，之后介绍基于事件时间的局部乱序度算法的设计与实现，最后介绍针对事件时间窗口水位线动态调整策略的设计与实现。

4.1 水位线设置大小分析

传统的水位线常为根据流数据乱序情况和计算需求而设置的静态值，但现实中多数流数据无法估计其乱序程度，而且大部分流数据内部乱序情况也不是稳定不变，而是会有局部弹性乱序的现象出现。

如图4所示。白色空心圆表示迟到程度较小的数据，灰色实心圆表示迟到程度中等的数据，黑色实心圆表示迟到严重的数据。横坐标为事件时间,即数据产生时间;纵坐标为到达窗口计算算子时间，理想水位线表示数据产生即实时到达，小水位线表示窗口关闭触发计算等待较短时间，大水位线表示窗口关闭触发计算等待较长时间。静态的水位线设置过小会导致大部分有价值的迟到不严重的数据无法参与窗口计算，从而降低窗口计算的准确性。水位线设置过大，虽然保证了大部分迟到严重的数据也能参与窗口计算，但在流数据乱序情况稳定或者不乱序的情况下延长了窗口计算的等待时间，从而降低了窗口计算的实时性。综上所述，需要一个可以根据数据流局部乱序情况动态调整水位线大小的策略来应对弹性乱序流数据，以保证水位线在流数据乱序严重的情况下升高使大部分有价值的数据也可以参与计算，水位线在流数据乱序稳定的情况下降低，使窗口计算触发不必等待过长的时间。

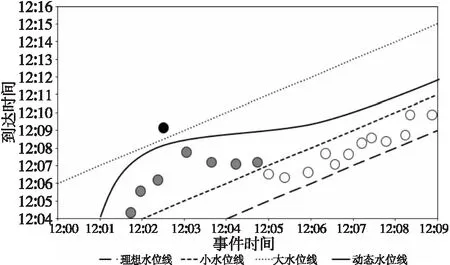
Figure 4 Contrast diagram of watermark 图4 水位线对比图

4.2 基于事件时间窗口的流数据微簇模型

本节针对弹性乱序流数据情况下基于事件时间的窗口计算建立数据流微簇模型。首先对本文所用到的变量进行定义。

ti：第i个到达数据所携带的事件时间戳。

N：当前时间点所到达数据中的最大事件时间戳，如式(1)所示：

N=max(ti)

(1)

M：设置水位线时的最大等待时间，即水位线的动态范围。

Tk：当数据流入计算数据流局部乱序度算子时，Tk表示当前数据流微簇，如式(2)所示：

Tk={ti+1,ti+2,…，ti+k}

(2)

其中，k为微簇大小。

P：当前时间微簇乱序程度，由微簇携带信息求得。

Wi：插入到数据流中携带时间戳的水位线。当前时间插入到数据流中的水位线Wi的计算如式(3)所示：

Wi=N-M*P

(3)

该模型针对事件时间窗口计算的水位线而动态调整，主要提出微簇机制来表示当前时刻流数据的乱序状态，微簇Tk中按数据流入算子顺序存储并实时更新数据流到达当前算子的最新k个时间戳，按照进入算子的先后顺序丢弃旧的时间戳，使微簇内部始终保持k个最新时间戳。乱序数据多为数据背压情况下各节点间网络传输速度不同、各节点性能和计算速度不同所导致的，因此不能确定的弹性流数据具有乱序程度局部聚集特性[16]。即严重迟到的数据几乎会聚集到同一时间段，同理乱序情况较弱的流数据也呈局部聚集状态，因此微簇中部分最新数据的乱序情况可以有效地表示当前时刻流数据的粗略乱序情况。使用该模型可以比较方便地求解。

4.3 基于事件时间的局部乱序度算法

以建立最优水位线调整模型为基础，可以设计出基于事件时间的局部乱序度算法,具体如算法1所示。

算法1基于事件时间的局部乱序度算法

输入：当前最新微簇Tk，微簇Tk携带当前最新k个已到达数据所携带时间戳信息和到达先后顺序信息。

输出：0～1的乱序度P。

Step1根据数据流微簇模型，算子内部创建状态存放长度为k的微簇Tk、当前乱序度P及当前数据流最大事件时间戳，微簇按到达算子先后顺序存储当前最新k个到达算子的数据事件时间戳。

Step2当有新的数据到达当前算子时更新微簇Tk内部事件时间戳和算子最大事件时间戳N，使微簇始终保持按到达先后顺序存储最新事件时间戳,如图5所示为微簇状态更新图。

Figure 5 Updating of microcluster state 图5 微簇状态更新图

Step3当微簇更新状态时，计算乱序度P，乱序度计算方式如式(4)所示：

(4)

其中，P表示当前微簇的乱序程度，其值在0～1，1表示微簇完全正序，0表示微簇完全逆序。

Step4更新乱序度P，即代表当前数据流局部乱序程度。

该算法根据流数据微簇模型中微簇的状态实时计算当前数据流的乱序度P。乱序度P由数据进入微簇的先后顺序和数据所携带的时间戳决定，乱序度越大表示当前微簇乱序程度越低，乱序度越小表示当前微簇乱序程度越高。

4.4 水位线动态调整策略的设计与实现

在并行集群中，流数据从数据源流入系统将根据编程逻辑结构被分配到不同节点的不同算子上，但因为计算资源不同和网络传输速度不同等原因会导致数据事件时间局部乱序或延迟等情况发生。为保证计算任务高效率完成，需要更准确的策略来调整水位线容错值。本文提出一种基于事件时间局部乱序度算法的水位线动态调整策略，其流程图如图6所示。

Figure 6 Flowchart of dynamic watermark adjustment strategy图6 水位线动态调整策略流程

具体步骤为：

(1)用户提交作业后，计算引擎会根据用户定义的数据源将数据流读取到分布式环境之中，并将数据按照编程的逻辑传递到各个节点上。

(2)流数据从数据源流入系统以后，系统内部会根据处理数据的内部逻辑对流数据进行分区、计算和处理。

(3)为不同并行度上的算子分配算子状态。该方法基于数据流微簇模型将当前算子流中的数据分为微簇，微簇时间戳数据存储在当前算子状态中。

(4)乱序度计算。当有新的数据流入算子时，根据微簇中的时间戳和基于事件时间的局部乱序度算法计算当前时刻的乱序度。

(5)当有新的数据流流入算子时，算子内部首先根据数据事件时间更新微簇内时间戳状态，然后根据微簇计算当前时间的局部乱序度。

(6)更新水位线最大允许乱序时间值。当计算出新的局部乱序度以后，根据局部乱序度大小调整水位线最大允许乱序时间值。调整方式如式(5)所示：

Wi=N-M*P

(5)

(7)更新当前最大水位线Wi，确保插入数据流中的水位线呈正序增加状态。

(8)当得到新的水位线以后，按照程序中设定的水位线周期将水位线插入数据流中并传递给下一个算子。

(9)当事件时间窗口收到大于窗口关闭的水位线值后触发窗口关闭并执行程序。

如图7所示，当水位线的允许乱序时间设置过大，会出现窗口无效等待的情况，从而降低了系统的计算速度；当水位线的允许乱序时间设置过小会使窗口丢失数据影响窗口计算的准确性。而本策略可以使最大允许等待时间动态变化，在保证系统计算准确性的同时降低计算延迟。

Figure 7 Window function图7 窗口函数

5 实验设计与结果分析

本文提出的水位线动态调整策略在Apache Flink 1.12中进行了实现，本节介绍实验环境和实验形式并根据实验结果进行分析，以证明该策略的有效性。

5.1 实验环境与实验设计

5.1.1 实验环境

实验环境是由4台机器搭建的Flink集群，集群具体参数配置如表1所示。集群设置1台主节点Master，3台从节点Node1、Node2和Node3。集群环境为CentOS 7.4.1系统，Java 1.8.0 版本。并使用Java语言进行程序编写。

Table 1 Configuration of flink cluster 表1 Flink集群配置

Flink集群支持Standalone cluster、Flink on Yarn和Flink on Kubernetes 3种模式，本实验采用常用的Standalone cluster模式进行集群部署。

5.1.2 实验设计

因为本文所提出的策略主要是针对窗口计算处理不同情况所导致的局部乱序流任务，所以数据集采用模拟生成的弹性乱序数据集，数据强度分别设置为10万，20万，50万，80万，100万和150万条流数据作为测试数据集，每次实验用尽数据集。为验证该策略和乱序度算法消耗的系统资源较小且在任务中可忽略不计，特设置每1 ms生成一条数据，根据马卿云等人[17]对同等级集群带宽传输开销测试，数据乱序程度分别采用3 s, 5 s, 8 s, 10 s和12 s延迟上下浮动。算法乱序度分别采用3 s, 5 s, 8 s, 10 s和12 s进行对比。实验采用流处理数据密集型任务WordCount作为窗口任务，窗口滑动距离20 s。并行度分别设为1,4,8,12,20和32。

5.2 实验评估标准

因为本文设计的实验为窗口任务处理不同乱序程度的流数据，故主要选取性能比作为评估标准,从有效性、鲁棒性、可扩展性和抗压性4个方面进行对比实验。

性能比根据式(6)计算：

(6)

其中,Ni为参与窗口计算的数据量，Ni越大即计算完整没有迟到数据或者低价值迟到数据越少，说明窗口计算准确性高；Di为窗口从开始到触发计算结束所用时长，即窗口计算时延，Di越小说明窗口计算时延越低,即实时性越高。m为开启窗口个数。性能比E即为平均计算数据量比平均窗口计算时长。性能比越高,说明计算兼顾准确性和实时性的能力越强。

5.3 实验结果与分析

5.3.1 有效性测评

本节分别为动态水位线算法和传统固定水位线算法设置不同的最大等待时间，实验结果如表2所示。

Table 2 Performance comparison of watermark algorithm with different algorithms out-of-order degrees表2 水位线算法在不同算法乱序度下性能对比

从表2中可以看出，最初最大等待时间太小限制了动态水位线算法的动态范围，所以性能比略差于传统固定水位线算法的；但是，随着最大等待时间设置的增大，动态水位线算法动态范围变大，可以更灵活地处理乱序数据，性能比也慢慢高于传统固定水位线算法算法的。

5.3.2 鲁棒性测评

本节分别为动态水位线算法和传统固定水位线算法设置不同程度的乱序数据，实验结果如表3所示。从表3中可以看出，面对不同乱序程度的数据流，动态水位线算法性能比均高于传统固定水位线算法的。但是，当数据流乱序程度高于动态水位线算法最大等待时间范围时，性能比会略微下降。这是由于不论动态水位线多灵活，也是有界限范围的，超出动态范围的严重迟到数据还是无法进入窗口计算。延迟超大的不确定弹性数据还是无法保证全部进入窗口计算。为了均衡实时性和准确性，有时不得不舍弃一些严重迟到的数据。而且，严重迟到的数据往往价值不大，大部分情况下舍去低价值数据避免过高的时延是非常有必要的。

Table 3 Performance comparison of watermark algorithm with different data out-of-order degrees表3 水位线算法在不同数据乱序度下性能对比

5.3.3 可扩展性测评

本节分别为动态水位线算法和传统固定水位线算法设置不同的并行度，其中模拟数据乱序程度设为8 s，算法最大等待时间设为8 s。实验结果如表4所示。从表4中可以看出，在不同并行度的情况下，动态水位线算法性能比上下浮动小，且均优于传统固定水位线算法的。这说明动态水位线算法和调整策略效果稳定，具有一定的可扩展性。

Table 4 Performance comparison of watermark algorithms with different parallelisms表4 水位线算法在不同并行度下性能对比

5.3.4 抗压性测评

本文分别为动态水位线算法和传统固定水位线算法设置不同强度的数据量，其中模拟数据乱序程度设为8 s，算法最大等待时间设为8 s。因不同数据量和固定的窗口长度导致性能比无法对比，所以性能比按数据量比例采用平均每10万条数据量进行计算。实验结果如表5所示。从表5中可以看出，面对不同强度的数据量，动态水位线算法的性能比均高于传统固定水位线算法的，且性能稳定。这说明动态水位线算法和调整策略在现有强度测试下效果稳定，具有一定的抗压性。

Table 5 Performance comparison of watermark algorithms with different data sizes表5 水位线算法在不同数据量下性能对比

6 结束语

本文针对传统固定水位线算法针对基于事件时间的不确定弹性乱序流数据的窗口计算无法同时兼顾准确性和实时性的问题，提出了基于局部乱序度算法的水位线动态调整策略。该策略基于流数据时间模型和局部乱序度算法对水位线进行动态调整。通过模拟流数据进行实验测评，分析对比了2种水位线算法的准确性和平均时长。实验结果表明，系统在保证大部分数据不丢失的前提下，缩短了窗口等待时间，提高了窗口计算的实时性，为因计算资源不同和网络传输速率不同等原因导致的数据弹性乱序情况下的窗口计算提供了可靠的保证。

未来将考虑在异构集群环境中不同节点计算性能差距明显的情况下进一步优化流计算模型，并考虑在更大的数据集上进行实验验证，以及在真实场景下进行应用，以测试系统平台效果，并优化流计算算法。