考虑二元Copula统计量的晶圆制造叠加误差监测
2023-02-20郝澜宇李艳婷潘尔顺
郝澜宇 周 笛 李艳婷 潘尔顺
上海交通大学机械与动力工程学院,上海,200240
0 引言
半导体技术一直是现代电子工业发展的原动力和重要基础[1],其应用领域包括新能源、信息通信设备、智能电网等。大多数用于微电子和光电子器件的集成电路是在其表面使用半导体晶片制造而成的[2]。晶圆是集成电路的主要原材料,其缺陷是影响产品合格率的主要因素[3]。晶圆制造过程复杂、漫长且成本高昂,必须在洁净室环境中进行数个化学步骤,例如沉积、刻蚀、光刻等,并且需要监控大量关键过程。在制造过程中收集传感器读数和晶片形状测量值等对工艺进行建模和监控[4],及时准确地检测缺陷,有助于质量控制,使产品达到更高的合格率。
晶圆数据具有高维特征,为后续的分析处理增加了难度。高维数据集应用越来越广泛,为更好地解释其含义,Pearson提出了主成分分析(principal component analysis, PCA)方法,既能以可解释的方式降低数据维度,也能保留数据集的大部分统计信息[5]。尽管PCA方法在工程、生物学、社会科学等领域都有着广泛的应用[6],但仍存在部分缺点。首先,对于高维数据,PCA方法计算量较大,同时因其不能产生稀疏主成分而很难给出合理解释;其次,PCA方法不稳定,鲁棒性较差,对异常值非常敏感[7]。为此,MARONNA等[8]提出了一种最小二乘法PCA(least trimmed squares PCA, LTS-PCA)模型以增加稳定性;SHEN等[9]提出了一种基于正则化奇异值分解的稀疏PCA(sparse PCA via regularized singular value decomposition, sPCA-rSVD)模型,通过获取稀疏主成分的方式来增强数据集的可解释性,但稳定性较差。最终,为同时解决稳定性和可解释性,WANG等[7]将LTS-PCA与sPCA-rSVD两种方法相结合,提出了一种基于最小二乘法的稀疏PCA方法(LTS-SPCA),计算更快速,模型更稳健,可解释性更强,但该方法在处理某些高维数据集时不够稀疏,导致模型复杂度偏高。
针对制造过程高维数据的异常监测,目前应用最广泛的是多元统计控制图方法[10]。考虑不同工程背景,现有大多数方法存在一定局限性。首先,缺少足够的先验理由,近似分布假设并不成立;其次,不同数据维度之间存在一定的相关性[11],大多数多变量监测过程并不独立[12];然后,变量之间依赖结构不灵活,不利于对数据的灵活建模;最后,多元统计过程往往缺少确定的联合分布来描述[13]。故将Copula模型引入多元统计控制图,其原理主要是将单变量的边缘分布函数和Copula函数进行组合,生成高维数据的联合分布函数,可用于构建灵活准确的多元分布[14],其中,Copula函数的选择取决于变量间的相关关系。FATAHI等[15]提出了一种基于Copula函数的双变量零膨胀泊松分布模型,基于所得的联合分布建立了用于监控稀有事件的双变量控制图。VERDIER[16]提出了一种基于非参数核密度估计方法的多元Copula控制图,由于Copula函数具有多种不同的分布族,适用于不同场景,故可以得到相对灵活的控制图,并证明在监测非高斯分布数据时,经典Hotelling T2规则可能产生许多误报。但通过密度估计方法构建Copula控制图仍存在一定局限性,如可能无法检测到受监控过程变量的多元分布形状变化,如果密度估计错误则会导致大批量误报等。KRUPSKII等[17]提出了两种新的基于Copula性质的多变量监测方法,对分布变化更敏感,并且不需要估计联合分布。
在晶圆制造中,数据维度高且耦合性强,其缺陷模式识别主要靠人工进行,现有大多数方法限于图像分类,无法分析缺陷的根本原因,且图像尺寸会影响到检索性能,故将机器学习技术引入晶圆缺陷模式识别可大大提高识别能力[18]。CHIEN等[19]开发了一种集成空间统计和神经网络的制造智能解决方案,用于晶圆地图模式的检测和分类,以构建一个在线监控和可视化系统,具有扩展的统计过程控制图。WU等[20]利用SVM对晶圆缺陷模式进行分类,并通过欧氏距离和二维归一化相关系数计算相似度,从而实现缺陷根源分析。YU等[21]提出了一种基于流形学习算法与高斯混合模型动态集成的晶圆缺陷模式识别方法。目前,基于离散数据的晶圆图缺陷模式识别在很多研究中都很常见,但针对后续光刻步骤中检测到的晶片重叠误差连续数据却少有人研究,具有挑战性和必要性。
本文结合晶圆结构中的置换特征和反射特征,开展芯片制造过程中的缺陷误差研究。针对高维连续晶圆数据难以准确监控的问题,本文在数据监测过程中充分考虑数据的可解释性,改进LTS-SPCA降维模型,提出灵活度较高的稳健稀疏主成分分析技术,然后建立一种基于Copula的多元耦合统计量异常监测方法。
1 晶圆制造叠加误差监测
晶片层与层之间的许多加工步骤都会引起整个晶圆的应力变化、扭曲或者形变,从而产生叠加误差。叠加误差可以体现所有过程中累积的应力变化[22]。图1展示了一个简化的晶圆叠加误差产生过程。首先,在晶圆上进行沉积工艺并快速暴露在热退火中[4],使自由状态的晶圆出现曲率。然后,将晶圆夹平,并在光刻工艺中进行图案化。为了生成第二层图案,需要改变晶圆的形状再沉积一个新层。最后,平整的晶圆被图案化。由于晶圆再次被压扁,第一层图案的距离增加,但新图案的印刷距离L保持不变,导致图案之间产生一定的错位,即叠加误差。
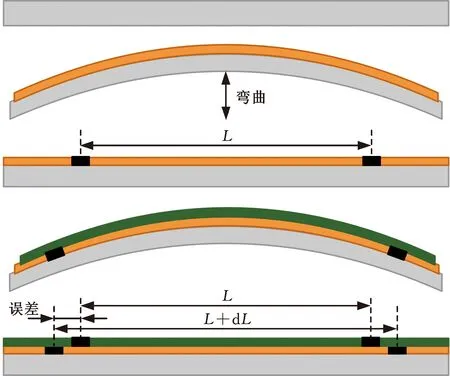
图1 晶圆片误差叠加过程[4]
数据集中包含大量正常情况和异常情况下的晶圆图像,以此为基础开展相关研究。其中,异常情况共有三种:X轴方向偏移、Y轴方向偏移和XY双轴方向偏移。图2是晶圆形状和其对应的在X轴方向上发生偏移的叠加误差异常图像。
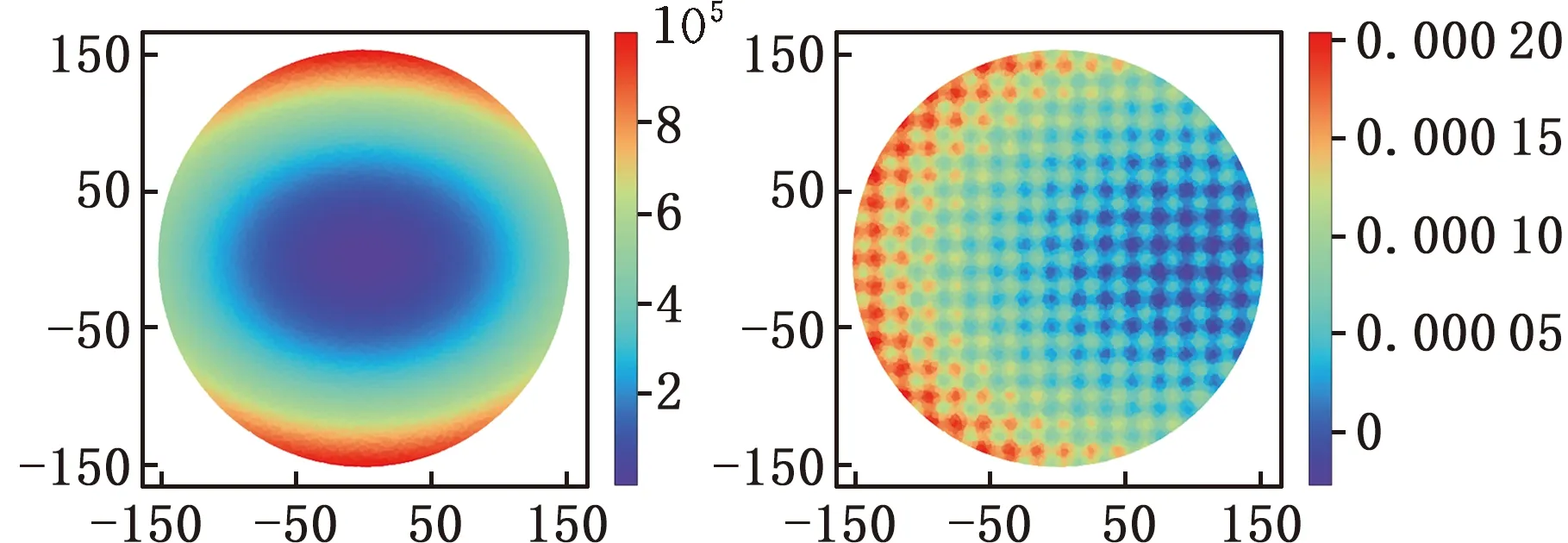
(a)晶圆形状(b)X轴方向叠加误差图像
晶圆异常图像主要由晶圆形状及其对应的叠加误差两部分组成,且晶圆形状会直接影响产生的叠加误差。考虑几种跨越不同空间波长范围的晶圆形状特征,确定晶圆的整体形状在几十微米的范围内弯曲。只考虑弓形结构和微观形貌,并假设在晶圆表面上沉积一层薄层,会导致晶圆形成弓形几何形状,公式如下:
(1)
式中,b1为弓形大小,设为100 μm;R为晶圆半径,设为150 mm。
然后进行光刻工艺,晶圆形状会发生弓形和波浪形变化:
(2)
式中,b2为弓形大小,通常在30~100 μm间均匀采样;hi、λi为对应的波高和波长;p为假定的波形数量[4]。
引入平面内变形(in-plane distortion, IPD)的计算公式:
(3)
其中,ω表示加工工艺前的晶圆几何形状。由此可见,IPD与晶圆形状的导数成一定比例。经过证明,可得
(4)
式中,ξ为常数,值为2/3;h为晶圆的厚度。
对于晶圆中的两层晶片i和j,分别计算Dip并相减,则可以得到形状-斜率差(shape-slope difference, SSD),即Dss=Dip,i-Dip,j。根据模型对SSD进行修正,可得形状-斜率残差(shape-slope residual, SSR)rss,进而得到平面内预测变形残差(predicted in-plane distortion residual, PIR)rpi的表达式:
rpi=c×rss
(5)
式中,c为一个常数,取决于晶圆厚度,通常取h/6[22]。
晶圆叠加误差主要是指制造过程中平面变形引起的图案错位,受晶圆形状、Dip和rss等多种因素影响。考虑到晶圆图像的基本结构是圆形,对应坐标轴方向,存在置换特征和反射特征。正常图像满足置换对称和反射对称的性质,而平面变形后的异常图像不满足。根据其异常形式的不同,共分为X轴方向偏移、Y轴方向偏移和XY双轴方向偏移三种误差表现形式。
本文研究过程的流程如图3所示。
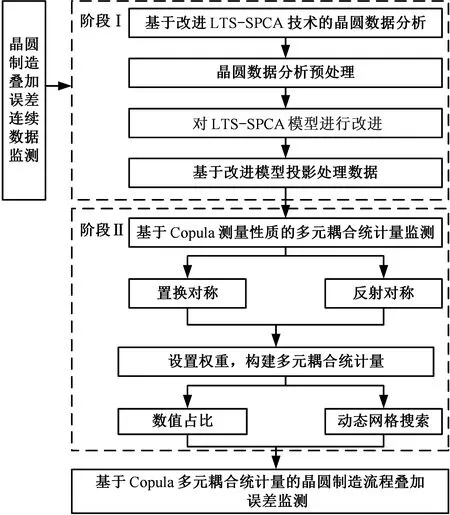
图3 研究过程流程图
2 基于改进LTS-SPCA技术的高维晶圆数据分析
2.1 晶圆数据分区预处理
从晶圆数据集中挑选1000张正常图像、1000张X轴方向偏移异常图像、1000张Y轴方向偏移异常图像和1000张X、Y双轴方向偏移异常图像,共4000组数据用于研究。
因晶圆图像中所包含的数据是高维且连续的,为脱离图像本身,将晶圆图像处理成只含有数据但不包含图形信息的数据,使图像尺寸不会对性能造成影响,因此需对图像进行分区处理。将整个晶圆地图按照图4划分为100个区域,可以看出,四角中共有12个区域会采集到无效数据,故将其剔除,得到88维有效数据。同时对数据进行去均值等处理后,可得到有效算例数据。
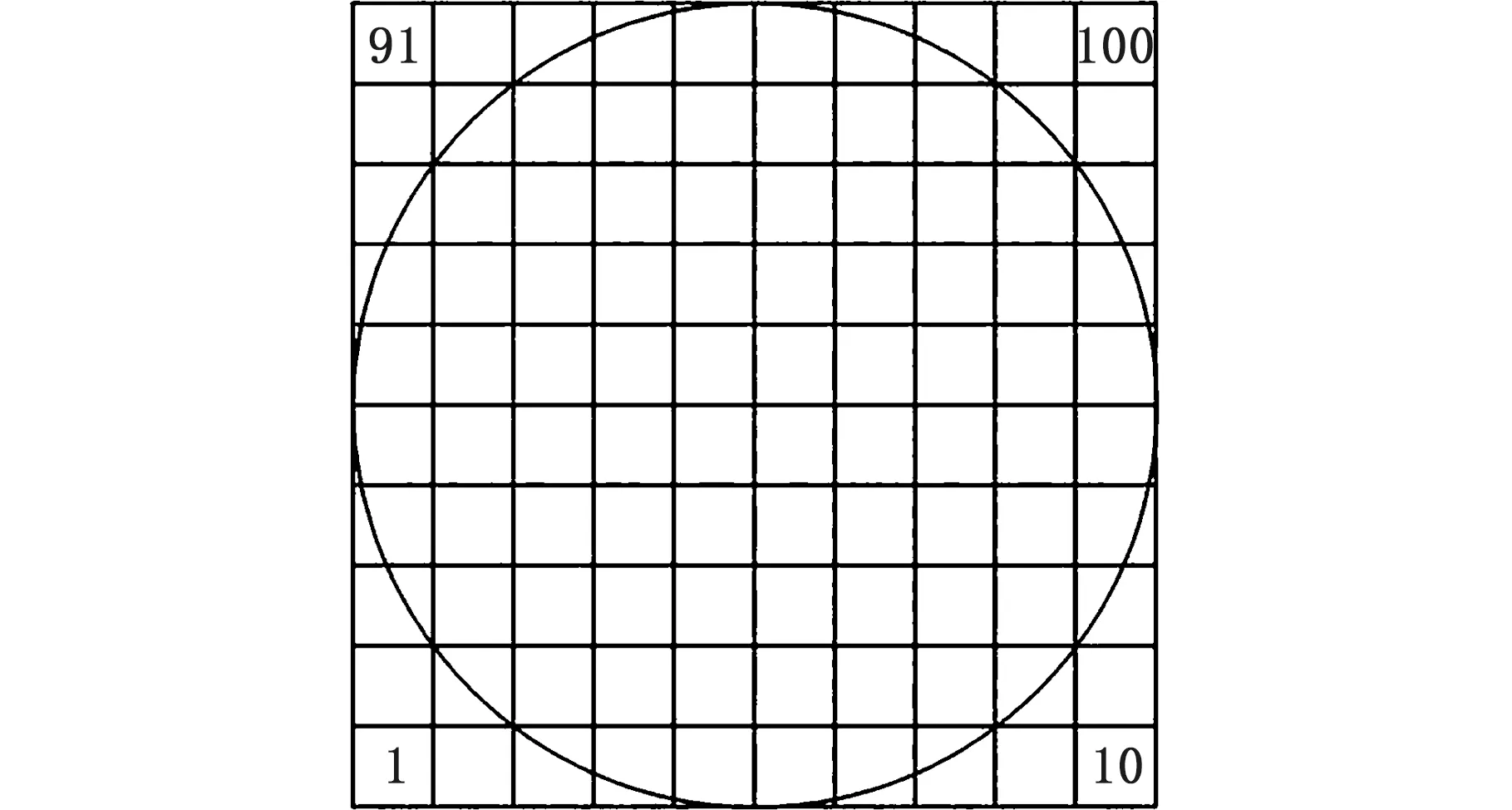
图4 图像分区示意图
图5是15个算例数据的前30个维度分布图,可以看出不同维度数据间存在较大差异性。晶圆图像中不同维度产生的叠加误差不同,规律性不强,差异性较大。为提高监测算法精度,适当减小计算量,对高维晶圆分区数据进行异常监测时需进行一定的预处理。
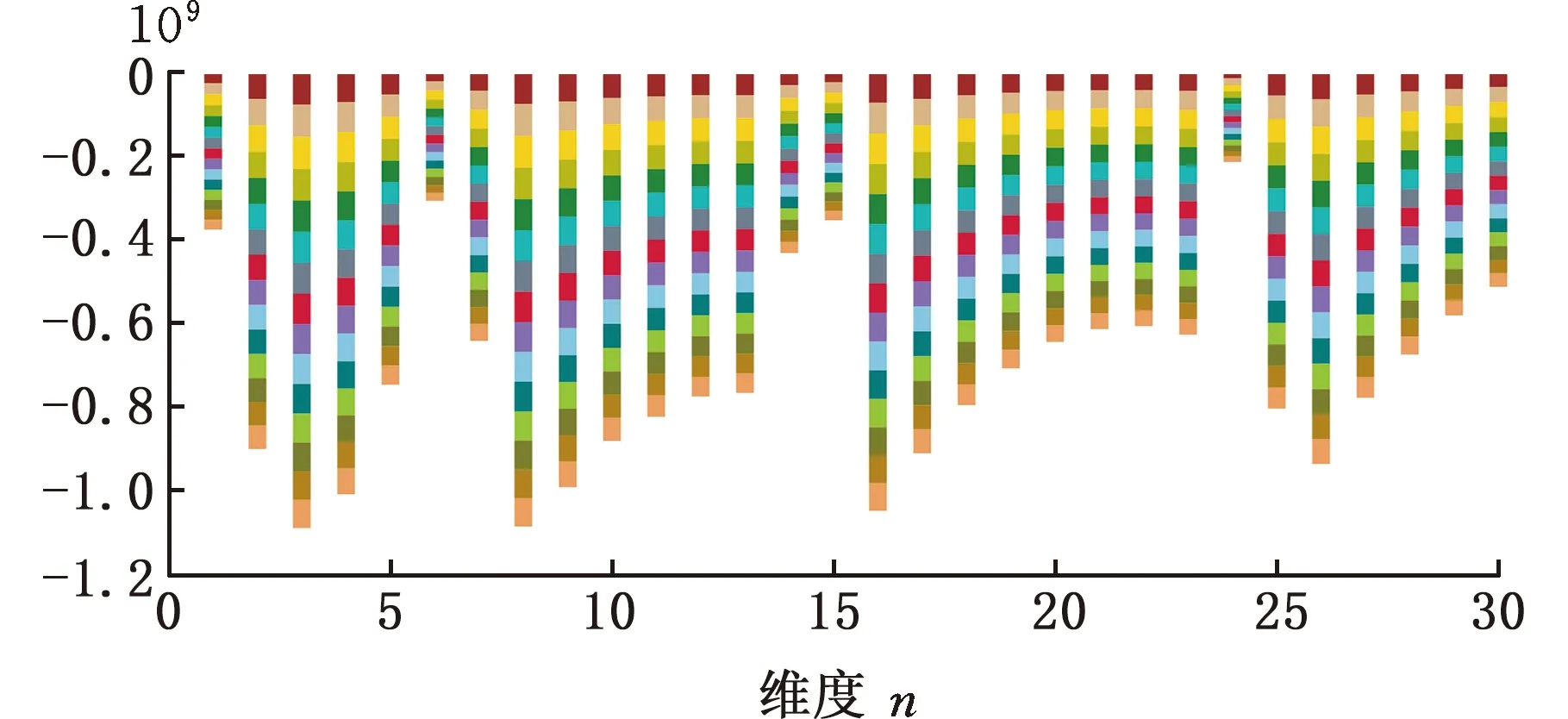
图5 算例数据分布图
考虑晶圆分区数据的维度差异性,对其进行简单统计及可视化处理。图6和图7分别是正常晶圆数据和X轴方向偏移异常晶圆数据所对应的箱线图,图8是两类图像的中位数图。由图6和图7可以看出,正常晶圆数据的分布相比异常数据更为分散。以图2b所示晶圆X轴方向叠加误差图像为例,发现异常图像因应力变化产生的变形会导致各维度的采集数据变小,符合数据分布规律。对比后可知,正常数据和异常数据的分布存在较为明显的差异,具有一定区分性。
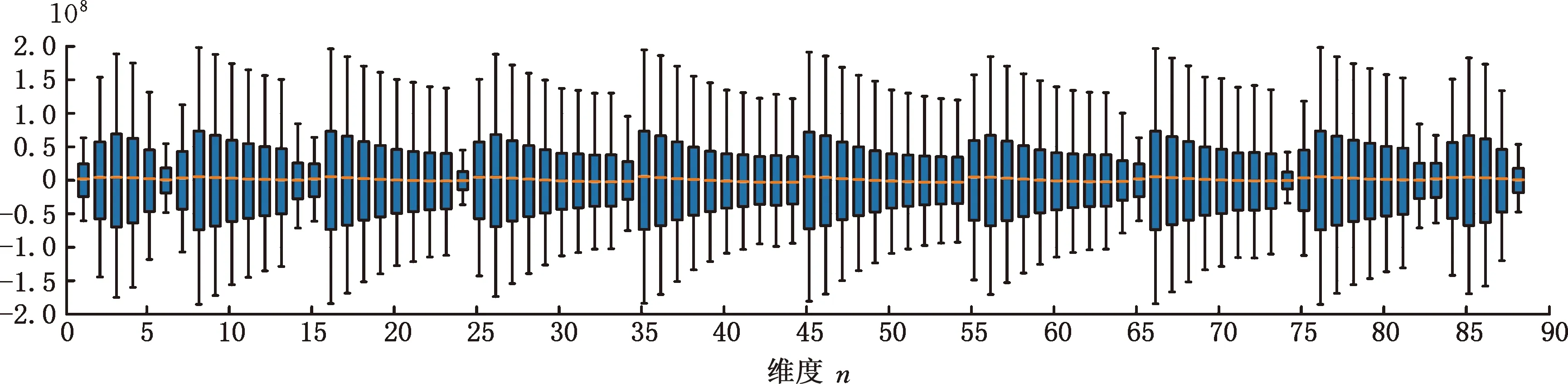
图6 正常晶圆数据箱线图
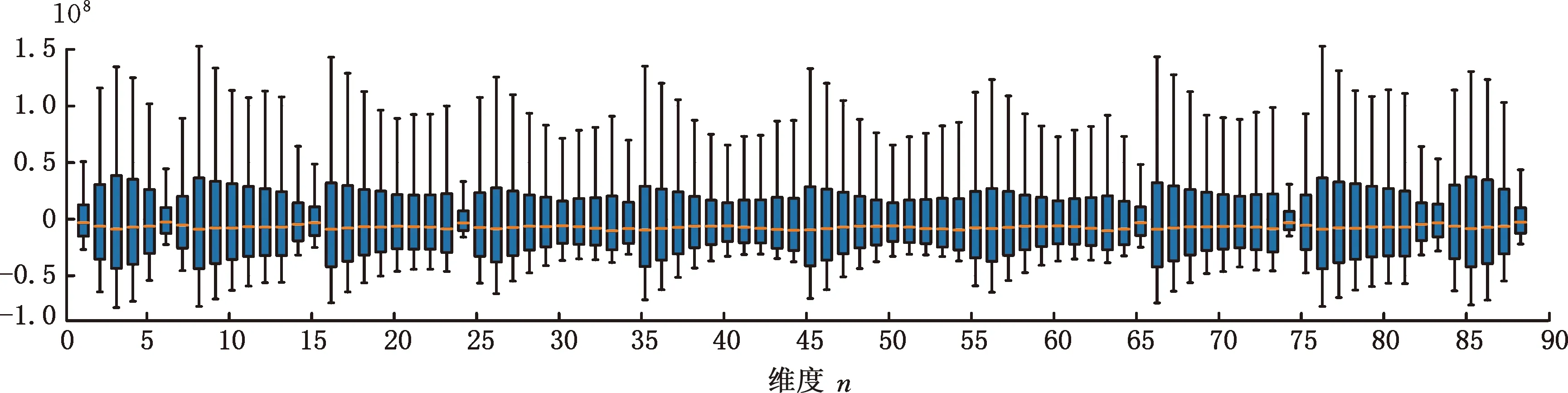
图7 X轴方向偏移异常晶圆数据箱线图
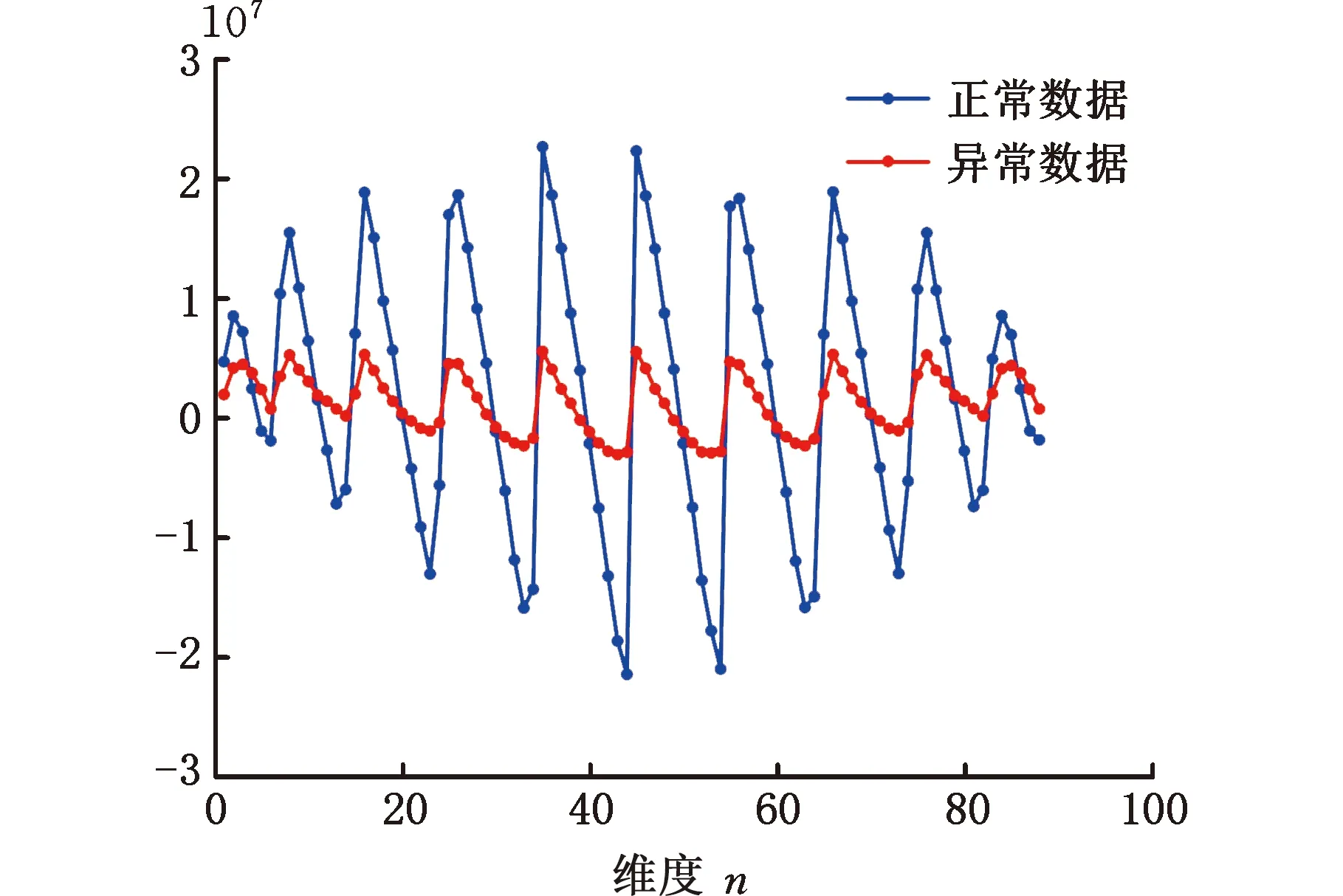
图8 算例数据中位数图
由图8可以看出,维度8、维度16、维度25、维度26等在两组数据中差异较大,能较好地判别数据是否偏移,而维度11、维度20、维度30和维度60等在两组数据中几乎具有相同的数值,对区分数据贡献不大。不同维度数据所包含的价值不同,故对算例数据进行整合降维处理是有必要的。由此,结合所构建的晶圆图像分区数据,展开高效的统计监测技术研究。
2.2 改进LTS-SPCA模型
考虑晶圆数据模型xi=μ+ρuiν+σzi,其中xi∈Rp(i=1,2,…,n),μ∈Rp是xi的中心,ui~N(0,1)是独立同分布的高斯随机效应,ν∈Rp且‖ν‖2=1是要估计的单个主成分,同时,zi~N(0,Ip)是独立的随机噪声向量。
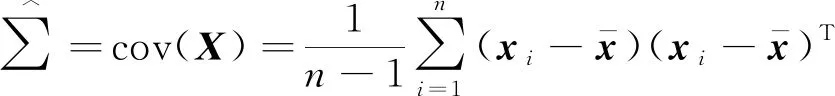
(6)
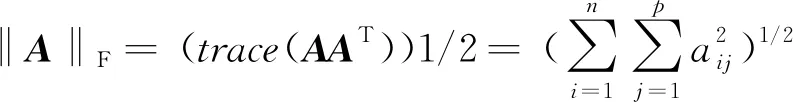
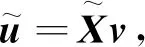
(7)
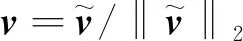
(8)
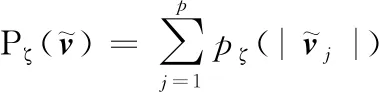
为增加稳定性,提出LTS-PCA模型[8],其目标函数可以表示为
(9)
U=(u1,u2,…,un)T∈Rn×k
V=(v1,v2,…,vk)∈Rp×k
式中,(·)h为子矩阵。
将问题(8)和(9)相结合,则可以估计出稀疏且稳健的主成分,得到LTS-SPCA模型[7],目标函数如下:
(10)
针对晶圆数据特性,在使用LTS-SPCA模型进行降维的过程中对其进行改进。在目标函数中加入新的惩罚项,在保证稀疏性的同时,限制各主成分中的各项系数不能过低,使其具有一定的物理意义。改进后的目标函数如下:
(11)
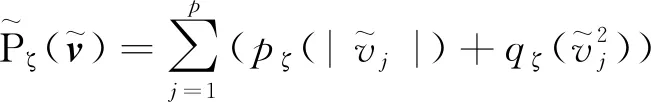
2.3 数据投影处理
晶圆数据集中共包含可用数据4000组,其中每类数据1000组。以识别X轴方向偏移异常为例,从正常数据和X轴方向偏移异常数据中各抽取600组作为训练集,各剩余400组用来测试模型效果。利用改进LTS-SPCA模型对晶圆数据进行投影处理,得到效果最好的2个稀疏主成分。图9为其对应的解释方差图,可以看出,前2个主成分数值偏大,整体占比较高,能更好地刻画晶圆特征。
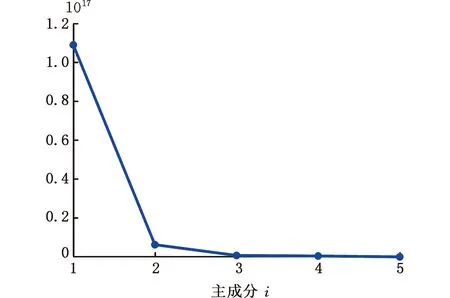
图9 解释方差图
图10是2个稀疏主成分所对应的各维度系数分布图。结合图像分区原则,对主成分所提取的区域进行标注,结果如图11所示。由图11a可以看出,第一主成分的系数较为分散,除维度44外,其余系数呈上下对称分布,分别对应图10中红色虚线凸起部分。由图11b可以看出,第二主成分的系数主要分布在4个维度,呈上下对称分布,分别对应图10中蓝色虚线凸起部分。
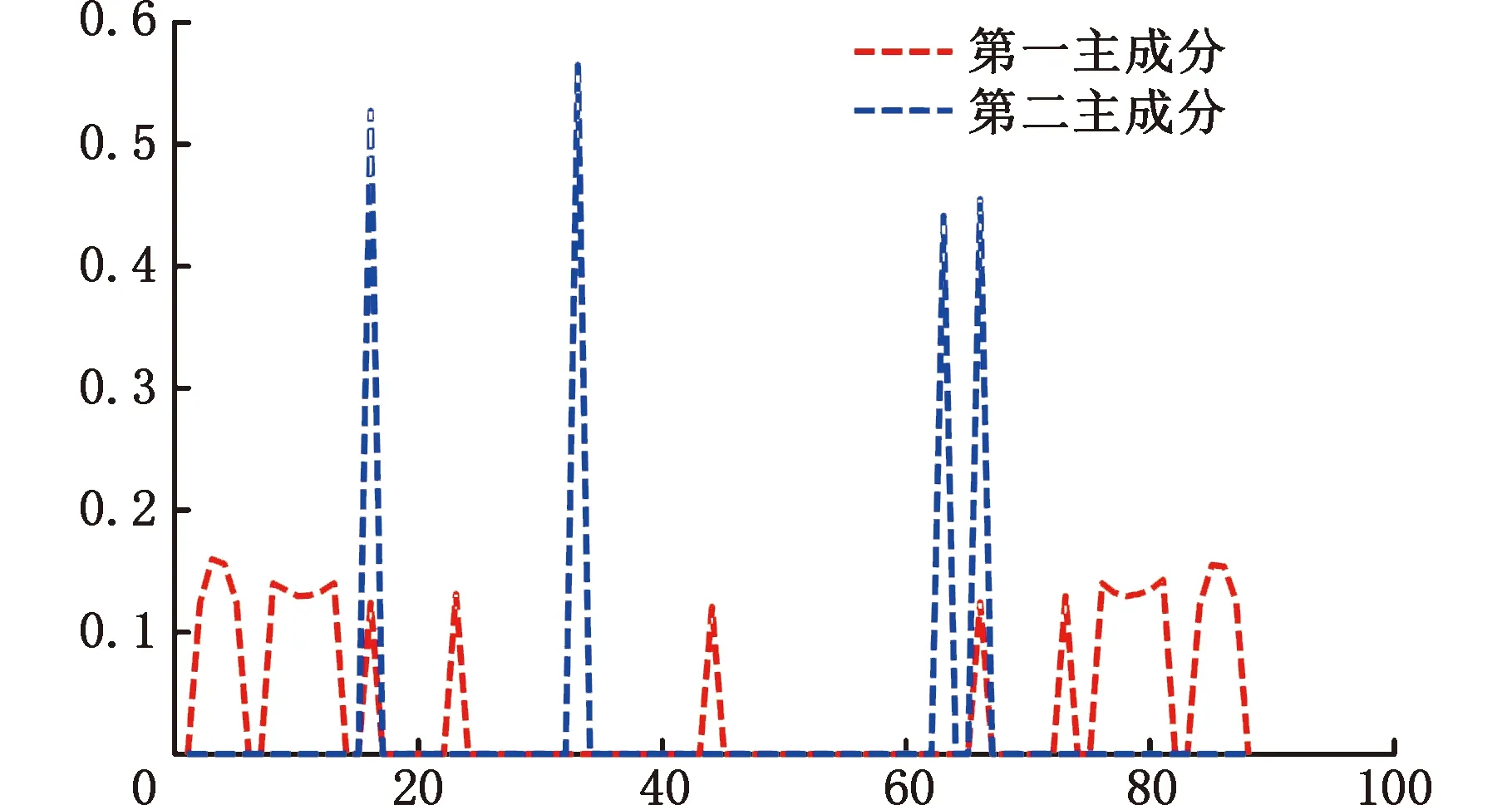
图10 各维度系数分布图
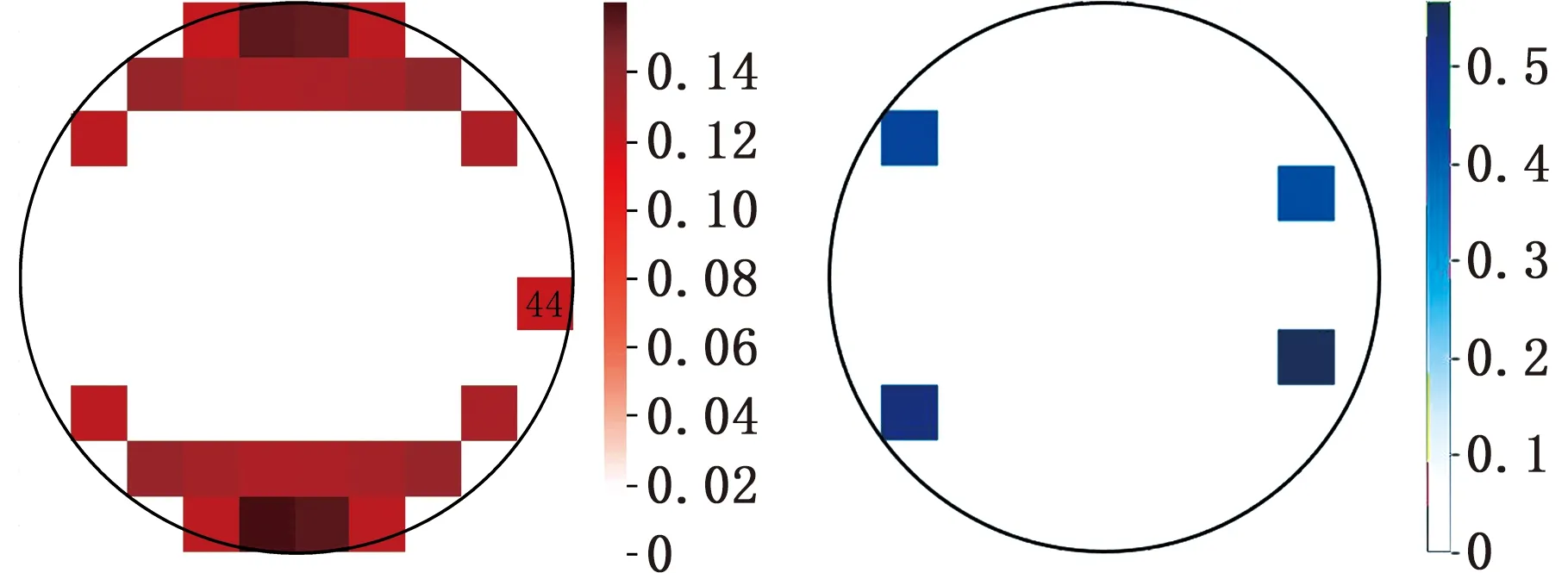
(a)第一主成分标注图 (b)第二主成分标注图
根据改进LTS-SPCA模型的计算结果对晶圆分区数据进行投影处理,筛选出有效数据。此时,88维数据被处理为2维投影数据,保留了绝大部分统计信息的同时还提高了数据的可解释性。利用改进方法实现数据降维技术,可通过较小的数据量监测出连续数据的变化,效率更高。
3 基于Copula性质的统计量监测方法
3.1 Copula性质
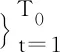
(12)
设c0为对应于密度f0的Copula分布,并令晶圆数据变量(U1,U2,…,Um)T的密度为c0。定义统计量ξk如下:
(13)
对于偶数k,统计量ξk可以检测整体依赖性强度的变化;而对于奇数k,则可以用来测量偏度变化。其对应的经验估计为
(14)
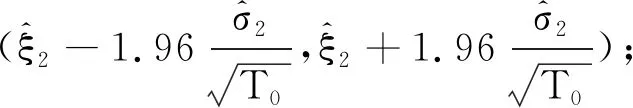
ξ2也可以看作皮尔逊相关系数的多元形式,公式如下:
(15)
其中,ρi1,i2=cor(Ui1,Ui2)是皮尔逊相关系数。不同维度数据间的皮尔逊相关系数越大,说明ξ2统计量的值越大。根据晶圆图像的结构特征,考虑对其置换对称性和反射对称性进行监测。图12所示是同一晶圆异常图像的置换和反射特征。置换对称性可以通过整体依赖性来测量。如图12a所示,以X轴方向偏移的晶圆异常图像为例,可得到其置换图像(图12b),说明统计量ξ2主要监测与坐标轴成45°角方向的数据变化。偏度是反射对称性质的一种体现[23]。如图12c所示,同样可以得到其反射图像,说明统计量ξ2k+1主要监测坐标轴方向的数据变化趋势。
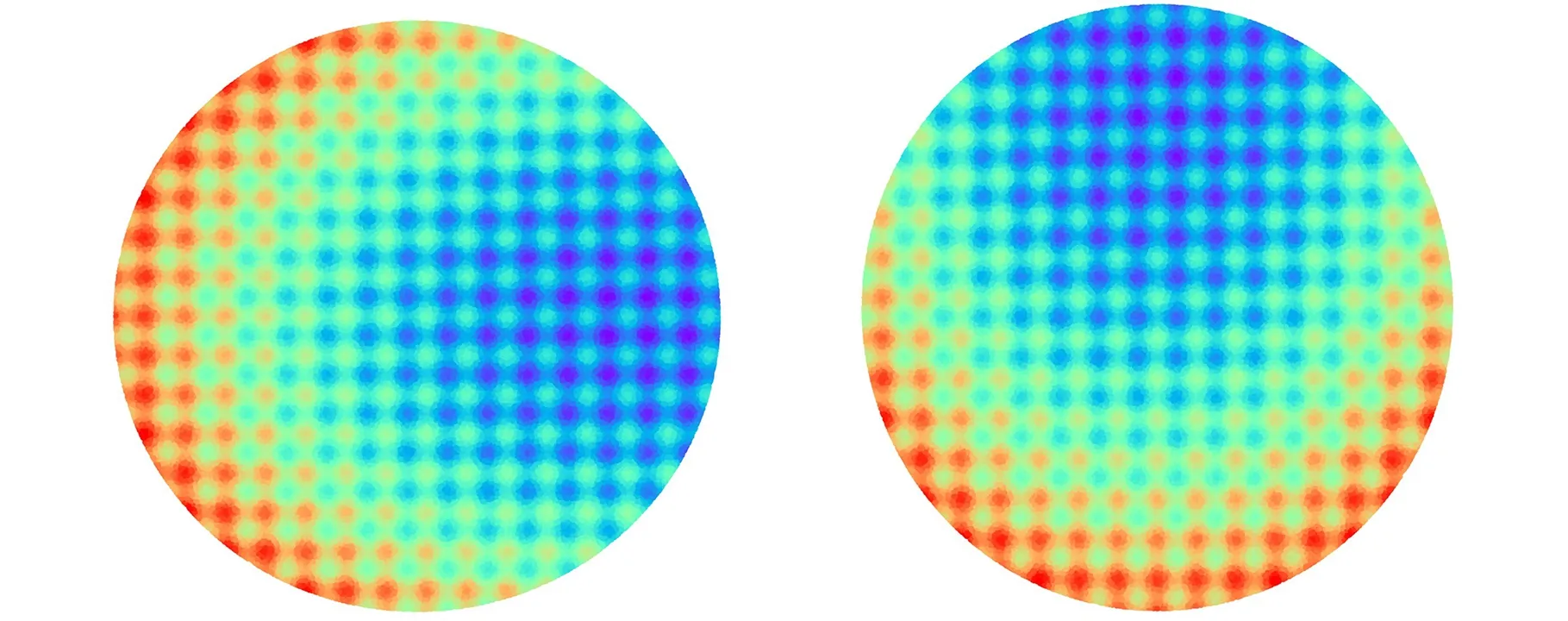
(a)晶圆异常图像 (b)置换图像
3.2 晶圆制造叠加误差的监测结果
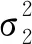
经过证明,当数据维度小于10时,统计量ξ7对函数反射对称性的变化最为敏感,故设参数k为3[23]。计算可得统计量ξ2的值为0.2480,所对应的置信区间为(0.2432,0.2528),异常数据监测准确率为83.95%;统计量ξ7的值为-0.0076,所对应的置信区间为(-0.0079,-0.0073),异常数据监测准确率为89.97%。图13和图14分别从不同角度展示了部分数据的监测结果及过程。图13共包含两个控制图,分别对应统计量ξ2和统计量ξ7的部分异常数据监测结果。在测试数据集中,存在部分数据未被统计量ξ2判定为异常但统计量ξ7监测出了其异常状态,例如数据点16等,同时仍存在部分数据未被统计量ξ7判定为异常但统计量ξ2监测出其异常状态,例如数据点5等。由此可得,同时监测基于置换对称和反射对称的两个统计量可有效提高异常数据的监测效果,在一定程度上互为补充。如图14所示,考虑到两个统计量数量级差距过大,需构建一种新的多元耦合统计量来更直接有效地监测数据异常。
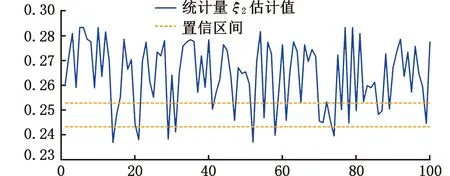
(a)统计量ξ2
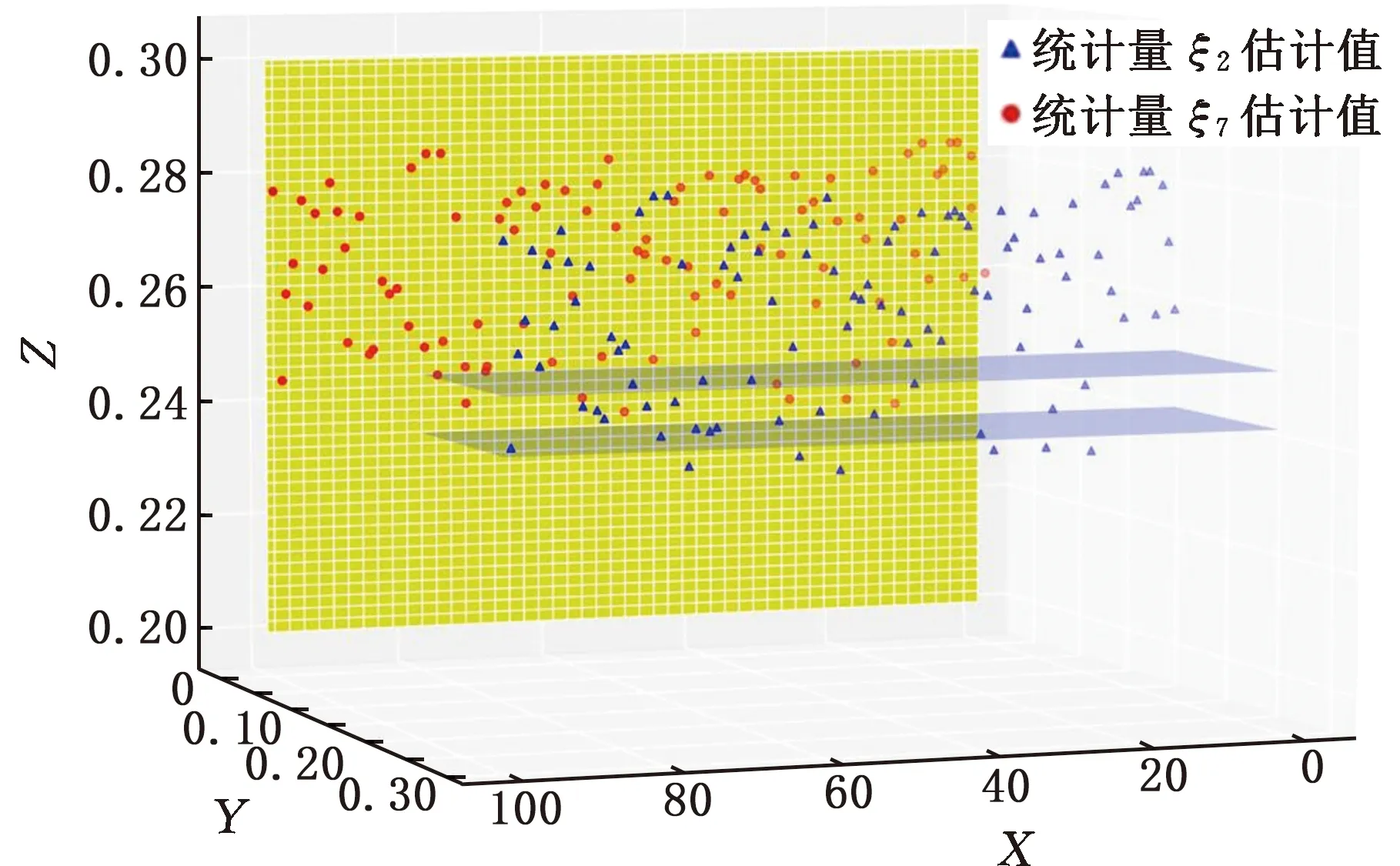
图14 监测结果三维图像
4 多元耦合统计量异常监测方法
为更好地结合置换对称和反射对称两种性质,需设置不同的权重值来构建一种准确有效的多元耦合统计量。权重的设置是否合理会直接影响其监测效果,因此,使用多种算法来计算统计量ξ2、ξ7对应的权重值ω2和ω7。考虑到其对应的数量级不同,可以通过数值占比方式确定权重,公式如下:
(16)
通过计算可以求出ω2的值为0.0306,ω7的值为0.9995,从而得到新的置信区间为(-0.0005,0.0004)。利用耦合统计量ξm监测异常数据集,可得准确率为90.64%。
同时考虑使用最优算法来计算统计量的权重,为消除数据间的量级差异,对其进行归一化处理。结合晶圆异常图像的结构特征可知,制造过程产生的叠加误差越大,其对应的统计量估计值越偏离正常经验统计量值,故两者之间的距离可作为评判标准。针对同一异常图像,与经验统计量值的距离越大说明耦合统计量的设计越有效。因此,最优算法的目标函数设为不同训练数据的多元耦合统计量ξn估计值与经验统计量值的距离平方和,同时为方便理解,约束条件中将权重之和定为1。具体问题描述如下:
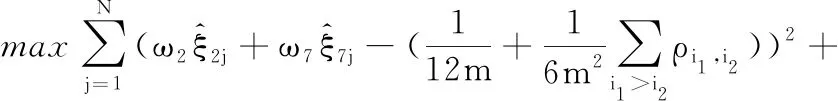
(17)
s.t.ω2+ω7=1 0<ω2<1 0<ω7<1

根据动态网格搜索算法求解,当训练数据集不同时,问题(17)对应不同的最优解结果如图15所示。由图15可以看出,随着训练数据集逐渐增大,异常监测的准确率呈波动趋势,而问题(17)的最优解逐渐收敛。根据ω2和ω7的收敛趋势,当ω2取0.3527、ω7取0.6473时,问题(17)得到最优解。此时,耦合统计量ξn的表达式为ξn=0.3527ξ2+0.6473ξ7。基于上文构建的晶圆异常模拟数据集,结合改进的LTS-SPCA降维模型对其进行投影处理,并利用多元耦合统计量ξn进行异常监测。异常数据共1200组,其中包括400组X轴方向偏移异常数据、400组Y轴方向偏移异常数据和400组XY双轴方向偏移异常数据。根据控制图建立流程,统计量ξn对应的置信区间为(0.0807,0.0844),监测异常数据的准确率分别为91.50%、91.25%和92.50%。图16所示为三类异常数据对应的混淆矩阵。可以看出,XY双轴方向偏移异常的监测准确率略高于其他两种偏移异常的监测准确率。通过对异常数据集进行监测可得,统计量ξn的平均准确率为91.75%。
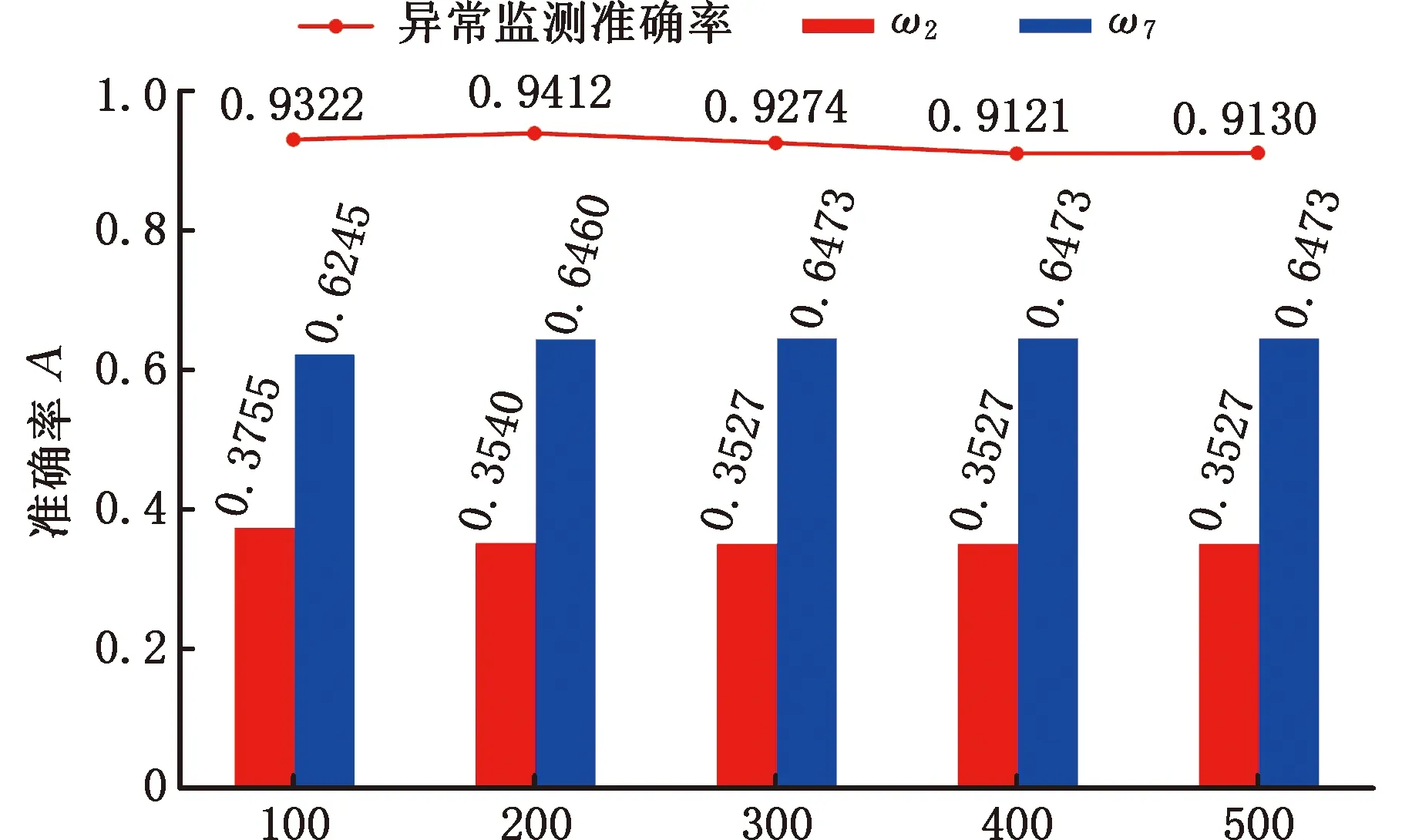
图15 动态网格搜索求解结果

(a)X轴方向偏移异常数据 (b)Y轴方向偏移异常数据
用于比较的监测方法包括多元耦合统计量ξm控制图、多元耦合统计量ξn控制图、基于置换对称的统计量ξ2控制图、基于反射对称的统计量ξ2k+1控制图、LTS-SPCA控制图、SPCA-Copula控制图和Copula控制图,比较结果见表1。由表1可以看出,所提出的多元耦合统计量控制图的监测效果明显优于其他几种方法。多元耦合统计量ξm和ξn异常监测准确率均超过90%,其中统计量ξn准确率最高,达到91.75%,实验结果证明所提方法能较准确地监测出晶圆数据异常。
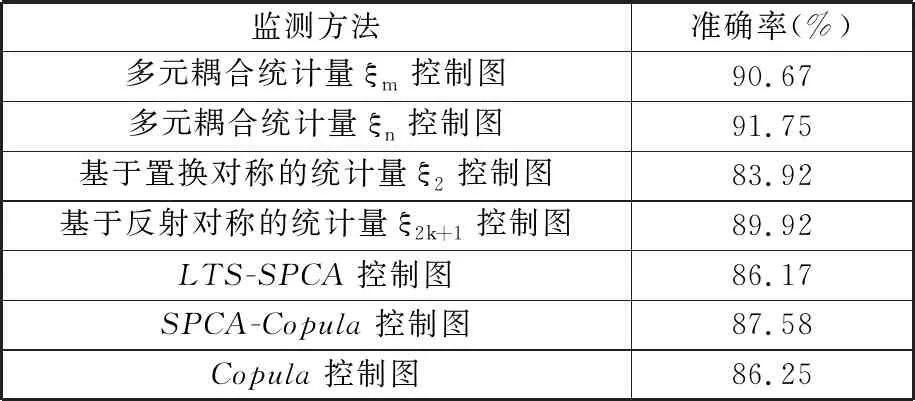
表1 模型比较结果
考虑晶圆制造过程中可能出现的加工误差、测量误差和人为误差等情况,本文在晶圆叠加误差数据模型中加入随机噪声扰动。针对X轴方向偏移、Y轴方向偏移和XY双轴方向偏移三种异常情况,各模拟出400组误差数据用于实验验证,发现新方法的平均异常监测准确率仍能达到90.58%。当噪声强度服从N(0,4)分布时,无噪声和有噪声两种情况下的部分异常数据监测结果如图17所示。由此可见,所提方法在无噪声和有噪声两种情况下都具有稳定的效果,能对晶圆制造过程中的叠加误差异常进行及时的监测预警,具有一定的普适性。
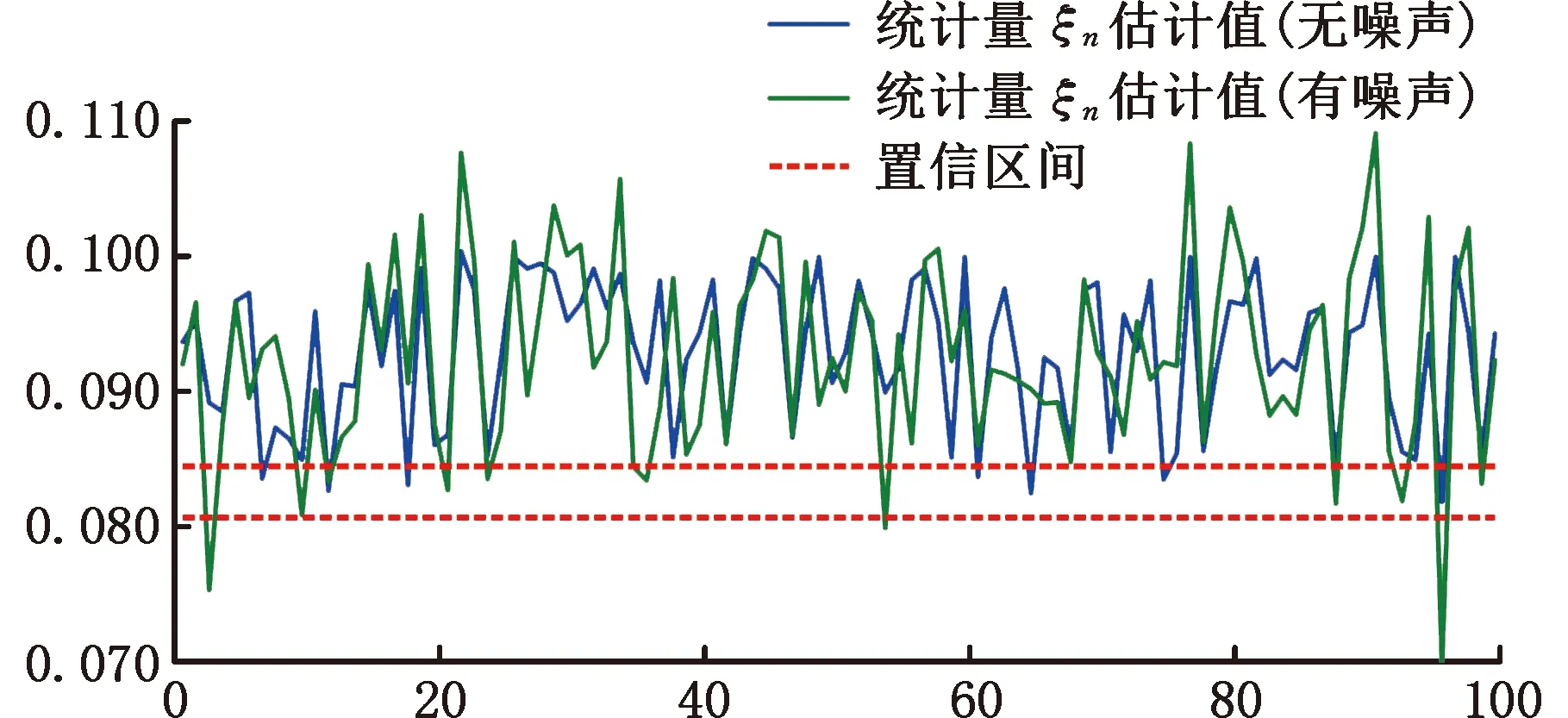
图17 部分异常数据监测控制图
5 结语
结果显示,所提方法监测异常数据的准确率可达91.75%,说明所提方法既可灵活有效地处理高维连续数据,又能有效结合Copula统计量准确监测制造误差,具有较高的工程应用价值。后续仍需进一步结合晶圆监测数据,丰富不同工况下数据集样本量,开展基于多元耦合统计量的晶圆制造误差高效监测技术研究。
