Linear analysis of plasma pressure-driven mode in reversed shear cylindrical tokamak plasmas

Ding-Zong Zhang(张定宗), Xu-Ming Feng(冯旭铭), Jun Ma(马骏),Wen-Feng Guo(郭文峰), Yan-Qing Huang(黄艳清), and Hong-Bo Liu(刘洪波)

1College of Physics and Electronic Engineering,Hengyang Normal University,Hengyang 421008,China

2Institute of Plasma Physics,Chinese Academy of Sciences,Hefei 230031,China

Keywords: magnetohydrodynamics(MHD),double tearing mode,pressure-driven mode

1. Introduction

Recently, renewed attention has been paid to the reversed magnetic shear profile for its capacity of obtaining higher bootstrap current fraction, forming internal transport barrier,and improving energy confinement.[1,2]Therefore,the reversed magnetic shear configuration is considered as an advanced operation scenario to reach tokamak steady-state operation. However, for such a magnetic configuration, it often encounters some problems,such as the degradation of energy confinement, decrease of the electron temperature, and even disruptions of plasma discharge.[3,4]It is believed that these behaviors are closely correlated with the resistive double tearing mode(DTM)for the existence of two rational surfaces in this configuration. In the device of Axially Symmetric Divertor Experiment (ASDEX) Upgrade, the DTM results in the breakdown of transport barrier and decrease of the electron temperature.[5]In the Experimental Advanced Superconducting Tokamak(EAST)2015–2018 campaign,all values ofβN=βt/(Ip/aBt)decrease during DTM phase,but present differentβNbehaviors thereafter (withβNrecovering or not).[6]Here,βtis the toroidal beta,Ipis the plasma current,ais the minor radius, andBtis the toroidal field on the axis. In the Japan Atomic Energy Agency Tokamak Upgrade (JT-60 U),m=3,n=1 DTM plays a crucial role in disruption.[7]

The typical characteristic of DTM is that there exist two rational surfaces with the sameqvalue (q=m/n). The distance between these two rational surfaces plays a significant role in the linear growth rateγ, mode structure, and the nonlinear evolution of DTMs.[8,9]If the distance between the two rational surfaces is large enough to ignore the coupling between two tearing modes on resonant surfaces, the linear growth rateγ, mode structure, and magnetic island evolution are essentially identical to those of the ordinary single tearing mode. When the separation of two rational surfaces is small, two tearing modes on rational surfaces are coupled together, leading to an increase in the linear growth rates of DTM.Its resistive scaling law can be estimated fromγ∝η1/3rather than the resistive scaling law of the single tearing modeγ∝η3/5.[10]Here,ηis the resistivity. In the nonlinear evolution process, the nonlinear behavior of DTM is also strongly associated with the separation between two rational surfaces.Under a certain inter-resonance distance, the inner magnetic islands and the outer islands expand toward theXpoints of each other, resulting in the formation of Sweet–Parker (SP)current sheets and the occurrence of flow-driven magnetic reconnection.[11,12]This explosive magnetic reconnection behavior may induce more complex nonlinear behavior, such as the formation and evolution of secondary islands and tertiary islands.[13–15]For sufficiently closed rational surfaces,high-mmodes may dominate over low-mmodes and the DTM has broad linear spectra.[16,17]Other effects on DTM, such as toroidal or poloidal shear flows,[18]Hall effect,[19]guiding field,[20]viscosity,[21]anomalous electron viscosity effect,[22]and self-induced Alfven resonance,[23]have also been investigated.

Most of the numerical studies of DTM are based on the RMHD model,which is deduced from the full MHD model in the approximation of high-aspect-ratio and low beta. However, the plasma pressure is often relatively large in actual tokamak plasma discharge, the low pressure approximation may not be preferable, especially in future high-beta fusion reactors, such as CFETR and ITER. It is found that a finite beta can lead to multiple branch instabilities of the DTM in small rational separation,and the effects of pressure on DTM are investigated.[24]In the present work, based on the full MHD model,[13–15]the unstable modes in the presence of twoq=2 rational surfaces are considered. It is found that the dominant mode undergoes a transition from conventional DTM to pressure-driven mode with the increase of pressure,which is consistent with the experimental results in ASDEX Upgrade.[5]Both the linear analysis of this pressure-driven mode (m=2,n=1) and its high order harmonics (m=2n,n ≥2)are studied.

2. Simulation model

2.1. Full MHD model

The instability considered in this paper is generated in the cylindrical tokamak with the plasma minor radiusaand major radiusR0. The non-reduced compressible MHD equations can be given as follows:

whereρ,V,P,J,B,ν,Γ,η,andEare the plasma density,velocity, pressure, current density, magnetic field, viscosity,adiabatic coefficient,resistivity,and electric field,respectively.

In the calculation,ν=1×10-10,Γ=5/3 and the following normalizations are used:ρ/ρ00→ρ,P/(/μ0)→P,V/VA→V,B/B00→B,J/(B00/μ0)=J,ν/(VAρ00)→ν,η/(a/τA)→η,r/a →r,R0/a →R0,t/τA→t, in whichρ00andB00are constants.VA=is the Alfven speed,andτA=a/VAis the Alfven time.

Within the scope of linear problem,each variable can be split into an equilibrium part and a perturbation part. For example,ρ=ρ0+, whereρ0and ˜ρdenote the equilibrium and the perturbation part of plasma density,respectively. Substituting this form of variable into the above equations,we can obtain

2.2. Numerical approach

Considering the periodicity inθdirection andφdirection, the perturbation ˜Xcan be expanded by Fourier series,e.g.,

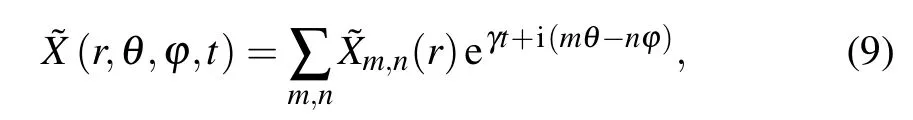
2.3. Equilibrium

The original equilibrium of safety factor is constructed as follows:

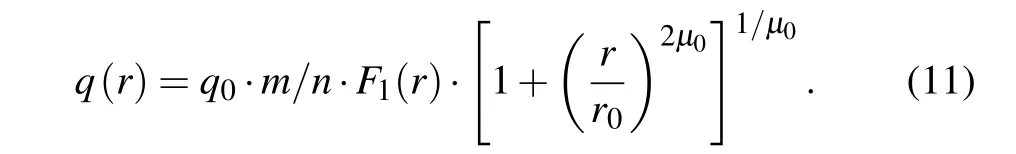
where

rA=0.655,μ0=3.8824,andq0is a constant, which is used to control the distance between the two rational surfaces Δr.The initial pressure profile is set to beP=P0(1-r2)2,whereP0=β0, andβ0is the beta on the axis. Unless otherwise stated,q0=1.293,andη=2×10-7. The initial radial profile of the pressure and the safety factor are both shown in Fig.1.

Fig.1.Initial equilibrium radial profile of the pressure and safety factor,with Δr denoting distance between two resonant surfaces.

3. Simulation results and discussion

Firstly, the characteristics of unstable mode with an extremely low beta (β0=1.0×10-6) are investigated. The results show that the unstable mode is essentially a DTM. Figures 2 and 3 show the eigenmode (unless otherwise stated,m= 2,n= 1) structures of radial velocity and radial magnetic field for Δr=0.1 and 0.3, respectively. In the case of Δr=0.1,the two resonant surfaces are well coupled with each other,and the amplitude of radial velocity is almost a constant between the two resonant surfaces (see Fig. 2(a)). This indicates that convection occurs mainly between the two resonant surfaces. The radial magnetic field is active in the region 0＜r ＜r2and primarily inr1＜r ＜r2as shown in Fig.2(b).Here,r1andr2denote the location of the inner and outer resonant surface, respectively. For the case of Δr=0.3, two individual modes each with a small amplitude near the two resonant surfaces can be clearly observed,and the radial velocity and radial magnetic field are greatly broadened (see Fig. 3).While other characters are very similar to those in Fig. 2. It needs pointing out that this broadening is mainly caused by the increase of separation between the two resonant surfaces.The above results resemble those in previous researches.[9,16]

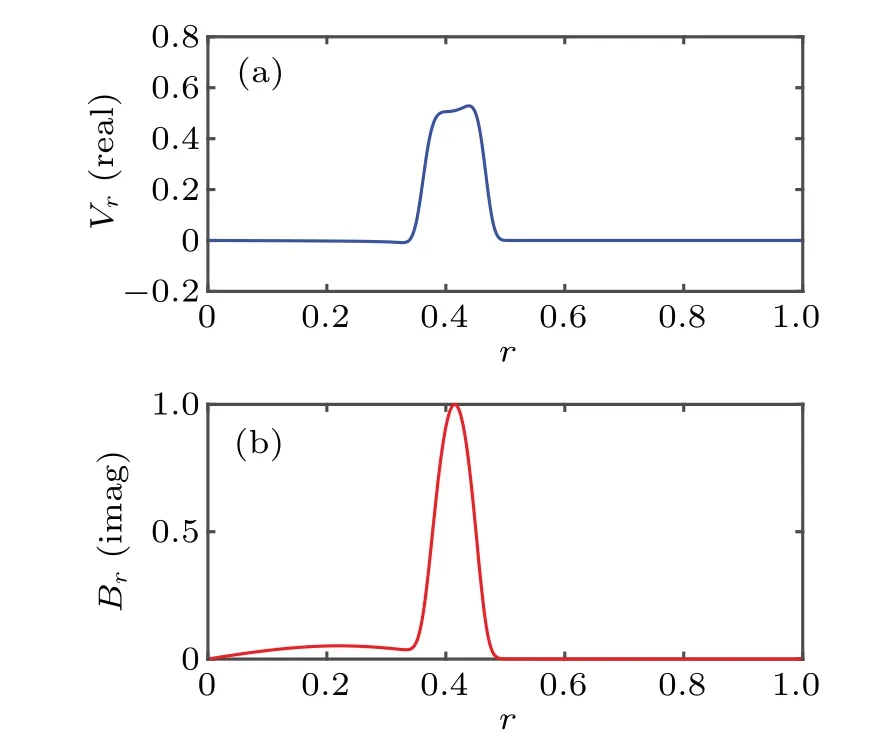
Fig.2. Eigenmode structure of DTM for (a) radial velocity and (b) radial magnetic field with Δr=0.1,with all variables normalized by max|Br|.

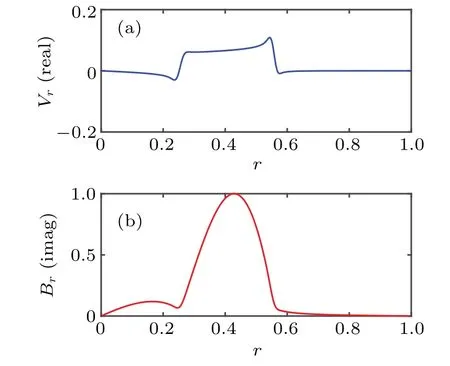
Fig.3. Eigenmode structure of DTM for (a) radial velocity and (b)radial magnetic field,with Δr=0.3.

Figure 4 shows the linear growth ratesversusplasma resistivity with different values of Δr. From Fig. 4(a) we can find that the growth rateγscales asη1/3when the Δris 0.1.With the Δrincreasing to 0.35,the scaling of DTM undergoes a transition fromη1/3toη3/5as shown in Fig. 4(b). These consist well with the linear theory about DTM.[8]

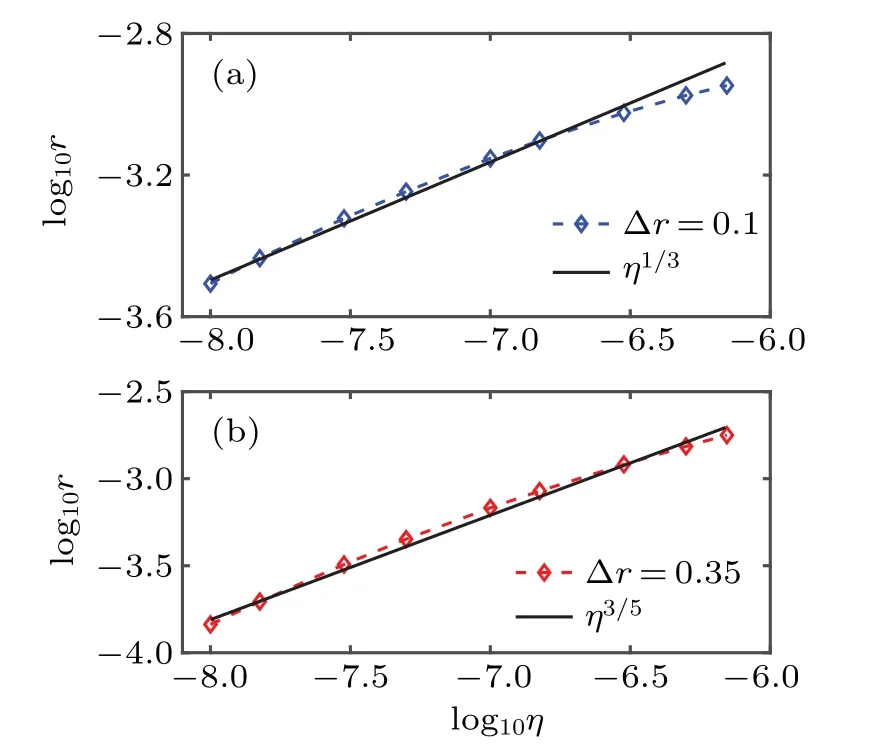
Fig.4. Linear growth rates versus plasma resistivity with different values of Δr.

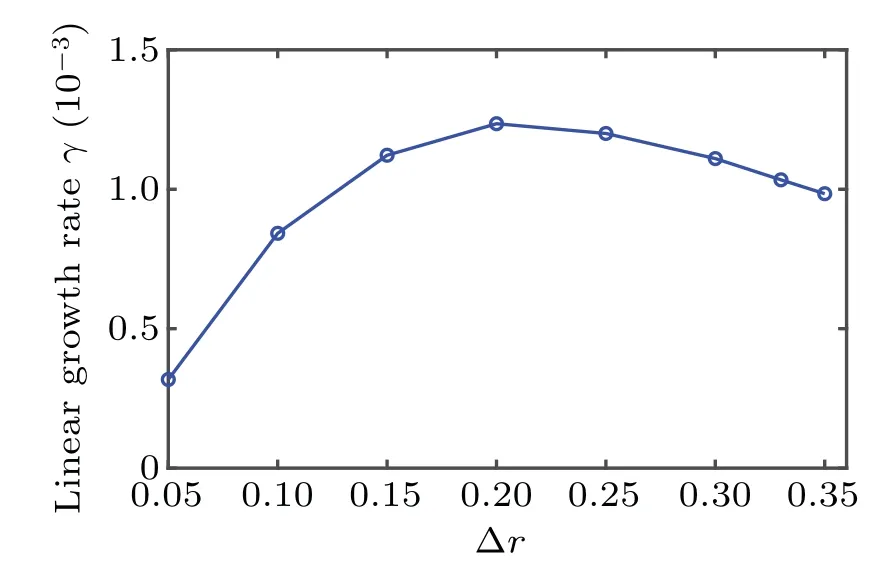
Fig.5. Variation of linear growth rate γ with Δr.

The dependence of growth rateγon Δris plotted in Fig.5 by changingq0in a range of 1.18–1.30,which corresponds to 0.05≤Δr ≤0.35. It is clear that the linear growth rate first increases and then decreases with the increase of Δr. This is in good agreement with the results of Fig. 7 in Ref. [5] and Fig.2 in Ref.[9].

To explore the unstable mode in high pressure regime,the eigenmode structure is plotted as indicated by blue lines in Fig. 6 with the plasma beta increasing from 1.0×10-6to 0.02, while other parameters are identical to those in Fig. 2.Interestingly, the amplitude of radial velocity increases from 0.5 to 0.84,accompanied by a wide broadening in 0＜r ＜r2,as shown in Fig.6(a). This is different from the typical DTM structure, in which the radial velocity is mainly restricted between two rational surfacesr1＜r ＜r2(see Fig.2(a)). In addition,an amazing change appears in the radial magnetic field(see the blue line in Fig.6(b)). The local maximum magnetic field value in 0＜r ＜r1becomes negative,and its magnitude is almost doubled inr1＜r ＜r2. This is also different from the radial magnetic field distribution of typical DTM.In DTM the signs of local maximum magnetic field in 0＜r ＜r1andr1＜r ＜r2are the same and the radial magnetic field is active primarily inr1＜r ＜r2. These differences imply that it may be inappropriate to regard this mode as a DTM. As is well known,the DTM is essentially a resistive mode. Considering this point, an additional calculation with the resistivity set to be 0 is conducted (see the red line in Fig. 6). Clearly,no obvious difference can be found except the amplitude of radial velocity. This shows that the resistivity has very little effect on the mode structure, which is also different from the effect of resistivity on the classical DTM.To sum up,the mode structure may be a result of plasma pressure instead of resistivity. Based on this,an inference may take place in the mode in Fig.6,which is essentially a pressure-driven mode.

Fig.6. Mode structures of (a) radial velocity and (b) radial magnetic field with β =0.02.

In order to confirm the above inference,the linear growth rate dependence on the plasma beta and resistivity are investigated. Figure 7 shows the effects of plasma beta on the linear growth rate,other parameters are the same as those in Fig.2.It is obvious that the linear growth rate increases monotonically with the augment of plasma beta. Figure 8 shows the effects of resistivity on the linear growth rate in the case of four different plasma beta values, in which the same results can be obtained, namely the linear growth rate is almost independent of the resistivity. Furthermore,in the non-resonant situation(qmin=2.001),the unstable mode can still be driven by plasma pressure.

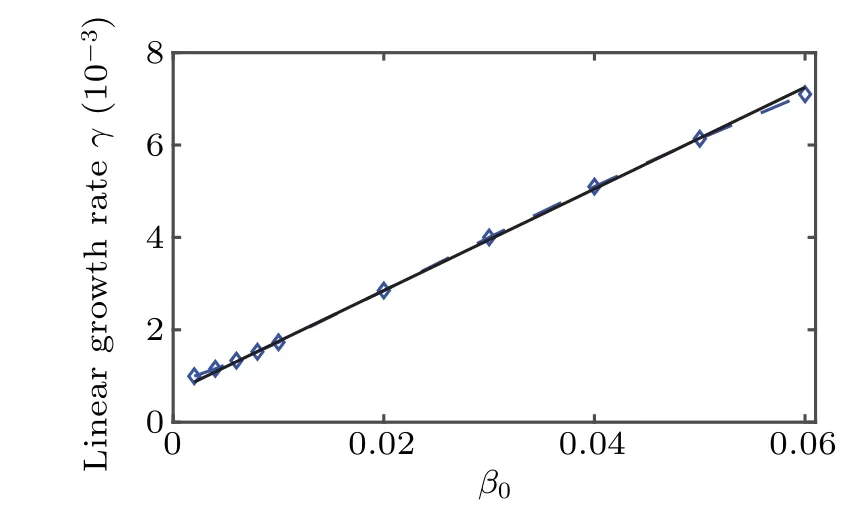
Fig.7. Linear growth rate γ versus β0.

Fig.8. Plots of linear growth rates γ versus η for different values of β0.

Summarizing the results of Figs. 2–8, we can conclude that a dominant mode transition from DTM to plasma pressure-driven mode occurs with the increase of plasma beta.This transition can perhaps explain the experimental results in ASDEX Upgrade.[5]It is found that in the discharge #12224 with pure NBI hearting (i.e., low beta regime) the unstable mode is DTM according to both experimental and numerical stability analysis. While in the discharge #12229 with combined NBI and ECRH (i.e., high beta regime), the unstable mode becomes an ideal mode driven by the pressure. In addition, the transition from ideal to resistive mode is observed during the decrease of the electron temperature (i.e., the decrease of the beta) as shown in Figs. 10 and 12 in Ref. [5],which is consistent with the numerical analysis presented in this work.In this pressure-driven mode(PDM),both the mode structure and growth rate are strongly affected by plasma pressure, while resistivity has very little effect. For simplicity,once the signs of local maximum magnetic field in 0＜r ＜r1andr1＜r ＜r2become opposite and the growth rate becomes a stronger relationship with plasma pressure than resistivity,the corresponding mode is regarded as being dominated by PDM.Figure 9 shows the plot of plasma beta needed for mode transitionversusΔr. It is found that the smaller the Δr, the more easily the transition to PDM can be triggered.

Fig.9. Plot of β0 needed for mode transition versus Δr.

In previous researches,[16,17]it is found that in small Δrthe high-mmodes may dominate over low-mmodes and the DTM has broad linear spectra. However, in these contributions,the effects of the plasma beta are not included due to the limitation of the reduced MHD model. Then,a straight question arises: “what is the case when the plasma beta is considered?” Motivated by this question, the linear growth rates of modes with different poloidal mode numbers are investigated for different inter-resonance distances and different plasma betas.

The simulation results show that although the nature of mode has changed fundamentally with consideration of the pressure, the high-mmodes (m= 2n,n ≥2) still dominate over low-mmodes in small values of Δr(see Fig.10,in which the growth ratesversusthe poloidal mode number for different plasma betas, with Δrfixed at 0.05, 0.1, and 0.2 are plotted).In addition,the growth rate of mode first increases and then reduces with the augment of poloidal mode number in the case of small Δr,and the mode number of the fastest growing mode shifts to highermmode with Δrdecreasing (see Figs. 10(a)and 10(b)), these consist well with the results of Ref. [16].Furthermore,in the case of small Δr,increasing beta can also result in fastest growing mode shifting to higher-mmode. For example,in the case of Δr=0.05(see Fig.10(a))the fastestgrowing mode is them=10 mode when beta is 1.0×10-6.When beta increases to 4.0×10-3,the fastest-growing mode turns intom=12 mode.Further increasing beta to 2.0×10-2,the fastest-growing mode shifts tom=16 mode. However,no dominant higher-mmodes are destabilized with the increase of beta in large Δr(see Fig.10(c)).

Fig.10. Variations of linear growth rate with poloidal mode number m for different values of plasma beta with(a)Δr=0.05,(b)Δr=0.1,(c)Δr=0.2.

4. Conclusions

Based on the full MHD model,the transition from DTM to pressure-driven mode is studied in reversed magnetic shear plasma. The results show that the plasma pressure has a significant influence on mode structure and growth rate. When the plasma pressure is small,the classical mode structure and growth rate scaling law of DTM can be obtained. However,the mode structure and growth rate undergo essential change when the plasma pressure is sufficiently large. Firstly, both the perturbed radial velocity and radial magnetic field are active in 0＜r ＜r2, and the magnetic field values are reverse in 0＜r ＜r1in mode structure. Secondly, the growth rate increases monotonically with the plasma pressure and is almost independent of the resistivity. Thus this mode can be regarded as a pressure-driven mode(PDM)instead of a DTM.The results presented in the work are consistent with the experimental observations in ASDEX Upgrade. The additional computation shows that the smaller the Δr(the distance between two rational surfaces),the more easily the transition to pressure-driven mode can be triggered off. Although the nature of mode changes fundamentally with consideration of the pressure, the high-mmodes still dominate over low-mmodes in the case of small Δr. Like the effect of Δron the growth rate in DTM,the growth rate of mode first increases and then decreases withythe augment of poloidal mode number in the case of small Δr, and the mode number of the fastest growing mode shifts to highermmode with Δrdecreasing. In the case of small Δr, increasing beta can also result in the fastest growing mode shifting to higher-mmode. While in the case of large Δr, no dominant higher-mmodes are destabilized with the increase of pressure.

In this work, we only consider the linear physics of pressure-driven mode in a cylinder plasma. However, the nonlinear behavior is also very important, which is one of the priorities of our next work. Generally, the flow induced by pressure-driven mode is stronger than that by DTM, and might cause stronger nonlinear evolution. The pressure driven in a cylindrical geometry plasma may be weaker than that in toroidal geometry plasma due to the toroidal effect. But the overall trend is consistent. In the future tokamak with high parameter operation, the linear and nonlinear behaviors caused by pressure will be more important.

Acknowledgements

Project supported by the Research Foundation of Education Bureau of Hunan Province,China(Grant No.21B0648),the National Natural Science Foundation of China (Grant Nos. 11805239, 12075282, and 11775268), and the Natural Science Foundation of Hunan Province, China (Grant No.2019JJ50011).