Vertex centrality of complex networks based on joint nonnegative matrix factorization and graph embedding
2023-02-20PengliLu卢鹏丽andWeiChen陈玮
Pengli Lu(卢鹏丽) and Wei Chen(陈玮)
School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China
Keywords: complex networks, centrality, joint nonnegative matrix factorization, graph embedding, smoothness strategy
1. Introduction
Complex systems from nature and society is modeled and represented by network composed of vertices,that denote entities, and edges, that correspond to the interactions between entity pairs,such as brain networks,[1]message networks,[2,3]human lives,[4]and social systems.[5]Scale-free characteristic of network demonstrates that the impact of different vertices on the function and structure may vary greatly and a few important vertices will affect the cascading effect[6,7]and propagation effect[8]of the network.Where the term“important vertices”means that certain vertices have a greater impact on the network structure and function to a greater extent than other vertices. Therefore,a key problem with important theoretical and practical significance is that of evaluation of vertex importance.
Many experts have made great efforts to evaluate the crucial vertices from different angles and presented many centrality algorithms. From the perspective of topological structure of network, they can generally be divided into two categories in general, which are based on local or global structure to determine vertex’s significance. Indicators based on local topology,for example,degree centrality(DC)[9]takes the number of edges connected to neighboring vertices as a metric.Denget al.[10]proposed a method based on the inverse-square law, named I, which defined intensity of vertex by the sum of mutual attraction between each vertex and other vertices.Zareieet al.[11]incorporated the notions of Shannon entropy and Jensen–Shannon Divergence to determine vertex centrality. Extend cluster coefficient ranking measure (ECRM)[12]is an improved cluster rank approach combining local clustering coefficient and similarity of connections between neighboring vertices. Node local centrality(NLC)[13]employs network embedding method and network neighborhood topology information to obtain the spreading capability of vertex.
The algorithms based on global structure tend to have relatively higher computational complexity than those based on local topology. For example, betweenness centrality(BC)[14]and closeness centrality(CC)[15]are based on the global path.K-shell(KS)[16]adopts the topological location of vertices and closeness to the graph core to sort them. In view of the shortcomings of KS,hierarchical K-shell(HKS)[17]introduces thepred,succ, andsiblsets to standardize the vertex’s topological position and estimates propagation capacity of vertex via its position and neighbors. Denget al.[18]proposed a novel method which takes into account the propagation characteristics of itself and all vertices. Besides,they provided a quantitative model(GIN)to measure the global importance of each vertex. Ullahet al.[19]have presented a global structure model(GSM) for influential vertices identification, which not only considers self-propagation characteristics,but also emphasizes vertex’s global influence in the network. In addition,the algorithms GLS and MCCD on the basis of the global and local structure of the network were proposed by Shenget al.[20]and Zhanget al.[21]
When using vertex centrality indicators to predict which vertices are among the top influencers or super communicators, comparative analyses have demonstrated that no single centrality algorithm is consistent in performance across realistic case studies. At the core of the algorithms to solve this problem is the assessment of important vertices with combining different attributes of vertex. Usually, multiple attributes describing a vertex characteristics are represented by a vector data. That is, for the verticesvi(i=1,2,...,n) in network,Ui=(ui1,ui2,...,ui5) means that the vertexvican be characterized by vector data with five attributes (for instance, the degree of vertex,the Laplacian energy of vertex,the central location of vertex,the propagation characteristics of vertex,the diversity of neighbors). Whenkattributes are used to characterize the vertex, the vector dataUiisk-dimensional, and the matrixU ∈is the attribute of the network.For integrating more attributes of the vertex, many algorithms incorporate multiple attribute decision making into the criterion to evaluate the importance of vertices,however,there are some unsolved problems. For example, indexes with different attributes are subjectively adopted as vertex attributes in the algorithm,which render it difficult to fully characterize the network and ignore the selected attributes whether linearly related.In the next place,the attributes of vertex and structure of the network are heterogeneous. Directly integration attribute and structure cannot effectively deal with the heterogeneity,which hinders the full utilization of them. In addition,for the increasingly large network data, how to more effectively represent attributes and structure information of network are also one of the issues we need to consider.
To overcome these problems,a new vertex centrality approach via joint nonnegative matrix factorization and graph embedding is proposed,referred to as VCJG centrality. VCJG is mainly composed of two major components: joint nonnegative matrix factorization obtains the attributes of vertex which fuse structure information, and the importance of vertices are evaluated applied attrubute and neighborhood rules.For automatically obtaining potential attributes, nonnegative matrix factorization(NMF)[22]is employed to decompose the weighted adjacency matrix. To capture the structure information of network, the global and local topology structure matrix generated by graph embedding are jointly decomposed via NMF. And we apply the smoothness strategy to integrate attributes,local and global structure information for overcoming the heterogeneity of them. Next, VCJG integrates the above steps to formulate an overall objective function,and generates an attribute matrix fused the structure information of network through optimizing the objective function. The above operation can ensure that each attribute obtained is linearly independent.Then we integrate the vertex attribute with neighborhood rules to evaluate vertex’s importance finally. To verify the effectiveness of the VCJG criterion, four traditional algorithms and five state-of-the-art centrality approaches are used as measures for comparison. And through extensive experiments on nine real-world networks, the results assert the proposed approach is superior to contrastive algorithms.
The rest paper is structured as follows. Section 2 briefly reviews the related works. In Section 3,a new centrality algorithm is proposed. We analyze the complexity of the proposed algorithm in Section 4. After that,we describe the real-world network datasets and experimental results in Section 5. Finally,Section 6 is the conclusion.
2. Related works
LetG={V(G),E(G)}be an undirected and unweighted network, with vertex setV(G)={v1,v2,...,vn}and edge setE(G)={e1,e2,...,em}, where|V(G)|=nand|E(G)|=m.The adjacency matrix ofG,denoted byA(G)=A,is then×nmatrix whose(i,j)-entry is 1 if verticesviandvjare adjacent inGand 0 otherwise. Letdibe the degree of vertexvi, andD(G)=Dthe degree diagonal matrix with diagonal entriesd1,d2,...,dn. The set of all neighbors ofviis denoted byNi,where|Ni|=di. The length of shortest path between verticesviandvjis represented asdistij. The maximum value ofdistijin networkGis called the diameter ofG,which is represented byDist(G)=Dist.
2.1. Presented approaches
In order to assess the impact of vertex more comprehensively, many scholars have designed centrality algorithms based on multi-attribute decision making. Duet al.[23]considered several different approaches as the multiple attributes and employed TOPSIS to aggregate the multiple attributes for measuring the vertex’s importance. Yanget al.[24]proposed a centrality method that apples VIKOR to integrate multiple centrality criteria from different angles and obtain comprehensive and reasonable ranking results. Yanet al.[25]comprehensively considered the multiple attributes of vertex and adopted the entropy weight method to get the corresponding weight of each criterion for overcoming the influence of subjective factors.
The above algorithms have been devoted to measure the importance of vertices from multiple attributes. However,these attributes are generated by multiple vertex centrality algorithms, resulting in correlations between them. For example,in view of the idea of the multi-attribute decision making,Yanget al.[26]regard DC, BC, and CC as vertex’s attributes,which have correlation because both BC and CC are based on global structure.In this paper,we will consider using the NMF algorithm to extract vertex attributes that are uncorrelated of each other.
2.2. Network embedding
It is not easy to take advantage of the structural information of the network(graph)because it is discrete by itself.As an example, individuals (vertex) cannot be added to each other, nor can an individual be subtracted from the relationship between individuals(edge). Quite a few researchers have begun to explore a kind of low-dimensional and dense vector representation method to represent high-dimensional network,namely network embedding.
Node2vec[27]learns continuous attribute representations for vertices in networks, which is an algorithmic framework.It has a flexible concept of a vertex’s network neighborhood and a biased random walk procedure, which can effectively explore diverse neighborhoods. Therefore, the mapping of vertices to a low-dimensional attribute space can be obtained to preserve the network neighborhood of vertices as much as possible.
2.3. Preliminaries
Lemma 1[28]A walk of lengthlinG, from vertexvitovj,is a finite sequence of vertices ofG,
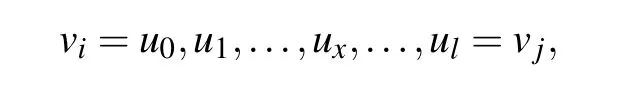
such thatux-1anduxare adjacent for 1≤x ≤l,whereuxrepresents the(x+1)-th vertex in the walk. The number of walks of lengthl, fromvitovj, is the entry in position (i,j) of the matrixAl.
2.3.1. NMF algorithm
The ubiquity of high-dimensional data not only leads to an exponential amount of computation which makes it difficult to ensure real-time processing,but also makes it difficult to mine the intrinsic structure and relevance of the data. Dimensionality Reduction is a data processing method that mines the essential law of data and discovers the internal relationship. Dimensionality reduction is divided into attribute selection and attribute extraction. Attribute selection is a subset of attributes that is extracted directly from the original data,and attribute extraction is a series of mathematical transformations that synthesize new attributes in place of the original data set.In this paper,non-negative matrix factorization(NMF)is used to extract attributes from the original network.
NMF is a method in matrix factorization algorithms that represents a matrix as the multiplication of simple and lowrank matrices. Since network can be expresses as adjacency(laplacian, signless laplacian) matrix, then a clear advantage for matrix decomposition in graph theory lies in the allowance of understanding the fundamental properties of graph and doing straight forward calculation.
Given a nonnegative matrixT ∈, nonnegative matrix factorization (NMF) aims to find two nonnegative matricesB ∈andF ∈such that the product of them can approximate the matrixT,i.e.,

Wherekis the rank of the matrix,usually(m+n)k <mn.[29]
Usually,we can understand that the column vector of the original matrixTis the weighted sum of all column vectors of the matrixB, and the weight coefficient is the element of the corresponding column vector of the matrixF,as shown in the following equation.For exampleSupport non-negative matrixsT ∈,B ∈,andF ∈R2+×3satisfyF ≈BF,i.e.,
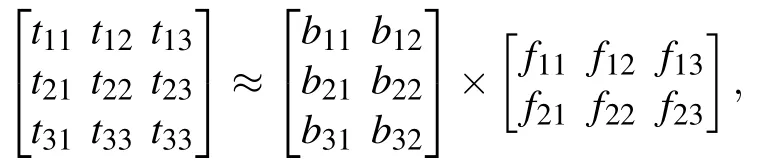
where
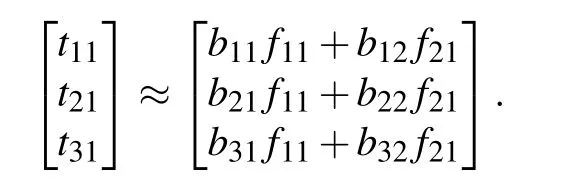
Therefore,it is called matrixBas the base matrix and matrixFas the attribute matrix.
3. Measuring the vertex centrality
VCJG is mainly composed of two major components:joint nonnegative matrix factorization obtains the attribute with linearly independent and fusing structure information,and the vertex’s importance are evaluated with attribute and neighborhood rules. In this section, they are described in detail.
3.1. Constructing objective function
The joint matrix factorization in VCJG involves three procedures,where nonnegative matrix factorization is adopted to generate the attribute of networks, the topological information is obtained by joint decomposing the topological matrix,the smoothness procedure connects the attribute and topology information of network. Therefore, the objective function of VCJG is composed of the costs of three programs.
The adjacent matrixAof the network characterizes whether there is interaction between the vertices, but it is not enough to fully describe the strength of it. Then,the weighted adjacent matrixW(Ref.[30])of the network is defined as follows:
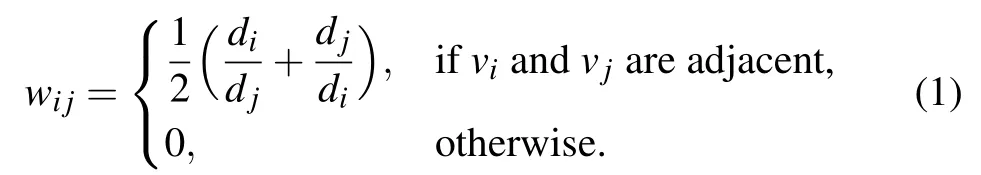
Obviously it is a symmetric nonnegative matrix. The most widely used strategy for obtaining network attributes is matrix factorization,we intuitively choose to use NMF,i.e.,

where theBis the basis matrix andFis the attribute matrix corresponding to matrixB, andkis the number of attributes.As can be seen from Section 2,Subsection 2.2.1,thekof factor matrix decomposed by NMF satisfies (m+n)k <mn. In this algorithm, the number of rows and columns of the original matrixWisn,then we have(n+n)k <n2⇒k <n/2.
The preceding equation can be solved by minimizing the squared error,that is,thel2norm between two matrices,
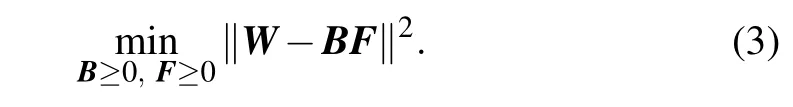
As is well known that social networks contain two different dimensions, where the structural dimension describes the interaction and composition dimension indicates vertex attributes. Therefore, only through Eq. (3) to obtain the attributes of the network is not enough to characterize the network. Considering that the topological structure is generally divided into global and local structures, we can obtain the topology information of the network through joint nonnegative matrix factorization.The adjacency matrix can only characterize the 1-order structure. Then for global structure,according to Lemma 1 we define the global topology matrixT gvia the matrixAlas follows:
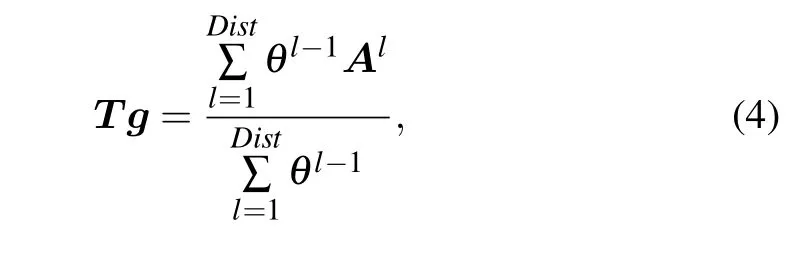
whereDistis the diameter ofGand parameterθ ∈[0.1,1]controls the relative weight of walks. (T g)i jis the weighted average of the number of walk from vertexvitovj. For local structure,since node2vec maps vertices to low-dimensional attribute spaces and maintains the network neighborhood of vertices as much as possible,we apply it to get the local structure matrixT lofG.
Here, we also use the same strategy by joint decomposingT gandT lunder the same basis matrixBto obtain the structure information of the network. The function is written as
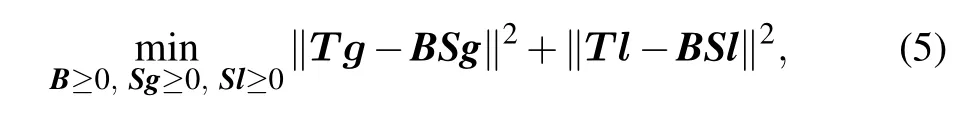
where the matricesSgandSlare local and global topology information, respectively. The attributes and structure of the network are heterogeneous, so the strategy we adopted is to smooth the attribute matrixFusing the topology informationSgandSl,i.e.,whereα ∈[0,1]is a parameter.

Considering that the decomposition process mentioned above is independent,we apply joint strategy to construct the objective function. By combining Eqs.(3),(5),(6),the objective function of VCJG is formulated as

where parameterαcontrols the direction in which the attribute is smoothed to the topology structure.
3.2. Optimal solution
From Eq.(7),we can obtain the multiplicative update solutions ofthe matricesB ∈,Sl ∈,Sg ∈, andF ∈by

where symbol⊙is Hadamard product.[31]It is worth noting that the matricesB,Sl,Sg, andFneed to be updated at the same time. According to the nature of NMF,the matrixFis a row non-singular matrix. Next,we give the proof of Eq.(8).
ProofBefore that, we first give the relationship between the Euclidan norm and the trace of the matrixA,i.e.,‖A‖2=Tr(ATA).
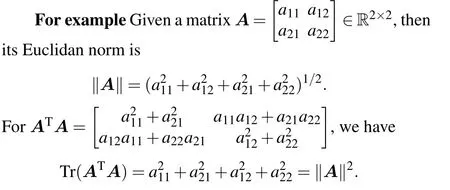
Return the above functionf, removing irrelevant items,equation(7)is reformulated as
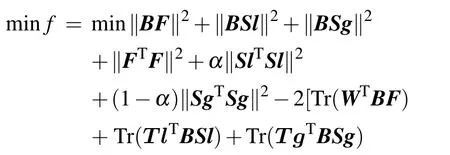
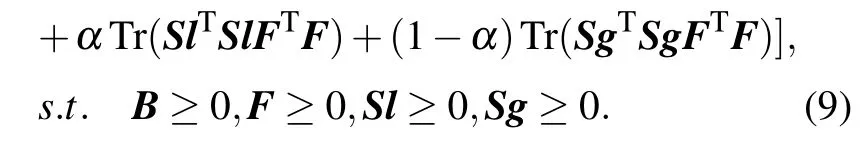
The alternative iteration based strategy is adopted to solve the above formula, where one variable is updated by fixing the others. We first solve the update rule of the matrixB. The matricesF,Sl,Sgare fixed,and irrelevant items are removed.The equation(9)can be rewritten as
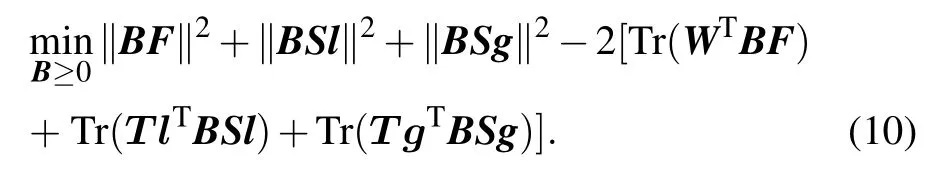
We use lagrangian multiplier method to deal with the nonnegative constraint of matrixB. Let beΦ=[φi j],the lagrangeℒof Eq.(10)is
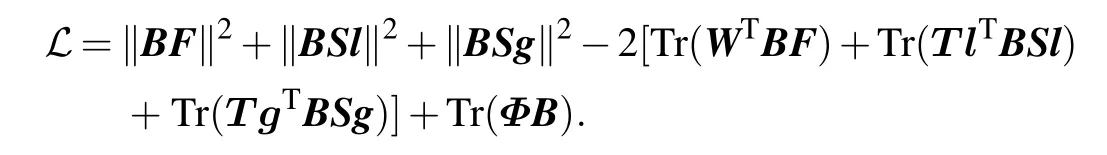
The partial derivative of matrixBis derived as follows:
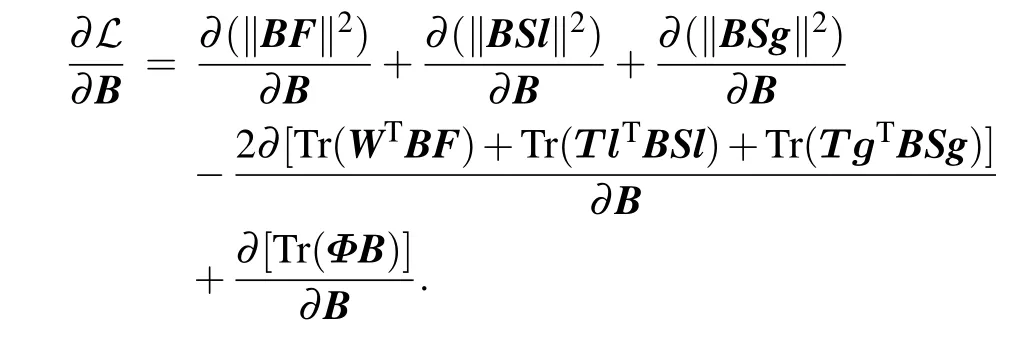
Respectively,according to the formulas
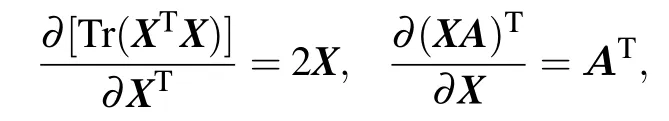
we have

Similarly,
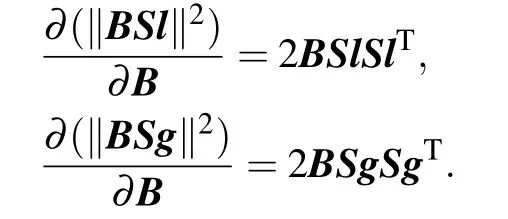
Next,according to the formula
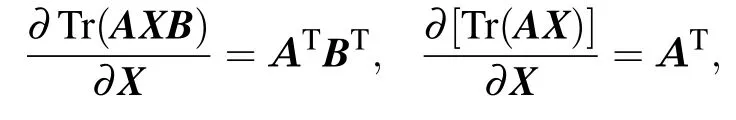
we have

Finally,
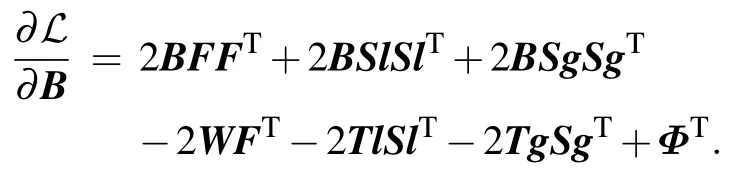
By setting∂ℒ/∂B=0, we obtain the updating rule for matrixBas follows in light of the Karush–Kuhn–Tucker(KKT)conditionφij(B)i j=0,i.e.,
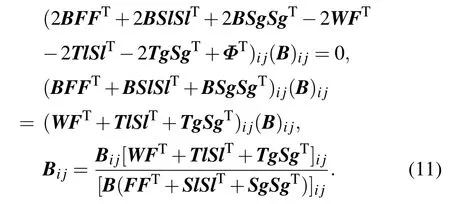
By fixing the matricesB,F,andSg,the update rule of the matrixSlcan be calculated. Let (λ)i jbe the lagrange multiplier for the constraints(Sl)ij,the lagrangeℒis

According to the formulas
the partial derivative ofSlis formulated as follow:

finally
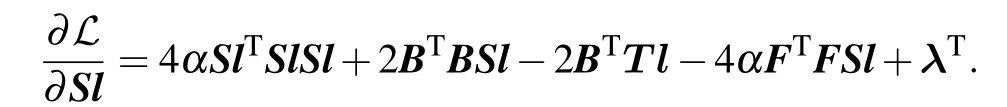
By setting the derivative ofℒ(Sl) with respect toSlas 0 and the KKT condition,we obtain the rule to update matrixSlas
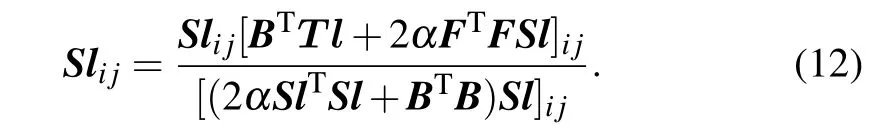
Analogously,the updating rule for matrixSgis as follows via fixingB,F,Sl
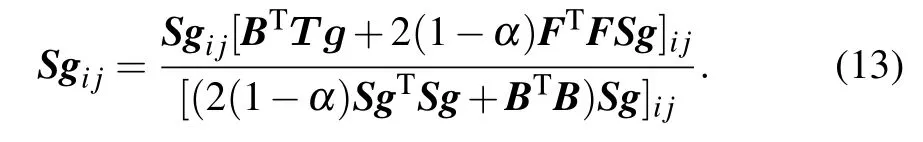
By fixing the matricesB,Sl,andSg,the updating rule for matrixFis formulated as

The above derivative formulas can be found in Ref.[32].
3.3. Evaluation of vertex essentiality
The previous parts mainly describes the construction of the objective function and the process of finding the optimal solution. By randomly giving the initial value of the matrices and iterating in light of the iterative formulas, we can get the attribute matrixFthat each attribute is linearly independent.However, our ultimate aim is to identify the most influential vertices in the network. The local structure considered in the objective function is the 2nd neighborhood of the vertex on the one hand, on the other hand, the application of neighborhood rules can improve the accuracy of determining the most influential vertices. Therefore,we apply the first-order neighborhood to evaluate vertex’s importance. Finally, the VCJG centrality is defined,as shown in Definition 1.
Definition 1 (VCJG centrality)
The matrixF ∈be the solution of Eq. (7), which is expressed the attributes of the network and each other is linearly independent. The VCJG (vertex centrality based on Joint nonnegative matrix factorization and graph embedding)centrality score of vertexviis defined as
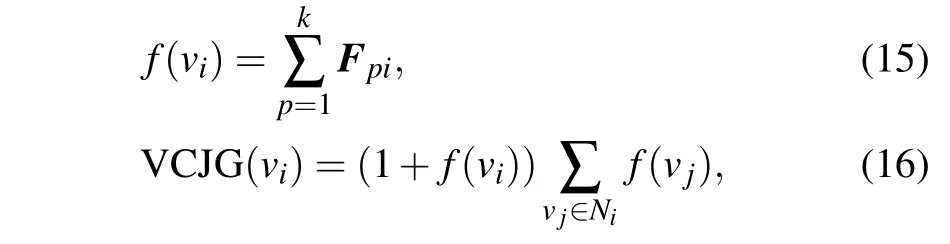
wherekis the number of attribute(usuallyk <n/2). The procedure of VCJG is illustrated in Algorithm 1.

Algorithm 1 The VCJG centrality algorithm
4. Algorithm analysis
The time complexity of VCJG centrality calculation is mainly composed of two parts,namely joint matrix factorization and vertex influence calculation. We need to spendO(n)for obtaining the matrixW. The time complexity for matrixT gisO(log(n)), which is calculated via matrix fast power algorithm. The time complexity for the graph embedding isO(n2). The running time for joint factorization isO(n2kr),whereris the number of iterations andkis the number of attributes. Then the time complexity of the first part isO(n2kr).TimeO(n×Dist)is required to calculate the influence of vertex,which is the second part. Finally,the time complexity of VCJG isO(n2kr).
5. Experimental analysis
In this section,simulation strategy and the results of evaluation measures are described in detail.To assess the proposed approach,we compare its performance with four traditional algorithms and five state-of-the-art methods including:
·degree centrality(DC);
·betweenness centrality(BC);
·closeness centrality(CC);
·k-shell(KS);
·the centrality based on the inverse-square law(I);
·hierarchical k-shell centrality(HKS);
·global and local structure centrality(GLS);
·global importance of vertices centrality (GIN) where parameters a and b are set to 1;
·the centrality based on global structure model(GSM).
These algorithms evaluate the influence of vertex from different attribute of vertex. DC algorithm takes the local topology attribute. BC and CC methods think about the global topology attribute. KS and HKS indexes consider the center location of the vertex. I algorithm considers the diversity of neighbors. GLS take into account both local and global topological attribute.GIN and GSM algorithms adopt the propagation characteristics.To illustrate the performance of JNMF,we use the four traditional methods and the five recent methods as baseline methods to build vertex centrality.
5.1. Utilized datasets
Nine different real-world networks, details about which can be found in Table 1,are used to validate the performance of the aforementioned algorithm.There are include karate club network (Karate),[33]the network of selling political books about the presidential election(Polbooks),[34]Jazz musicians network (Jazz),[35]usair network (USAir),[36]co-authorship network of scientists (Netscience),[37]Email network of the University Rovira i Virgili (Email),[38]protein–protein interaction network (Yeast).[39]The user network of the hamsterster.com website (Hamster)[40]and the network of the online social networking platform(Facebook).[41]The statistics characteristics of these datasets are summarized in Table 1,whereβthis the infection rate threshold andβis the optimal infection rate value.

Table 1. Statistical characteristics of all datasets.
5.2. Experiments for the parameters
Recall that VCJG involves three parameters: parameterkdenotes the number of potential attributes,parameterθdetermines the weight of thel-order global topology, and parameterαgoverns the direction in which the vertex attributes are smoothed to the topological structure. All possible values of each parameter are considered and ranking lists under these combinations are calculated. The Kendall coefficientτis used to evaluate the correlation between the ranking and the ranking generated by the SIR model,and finally the value of each parameter is determined.
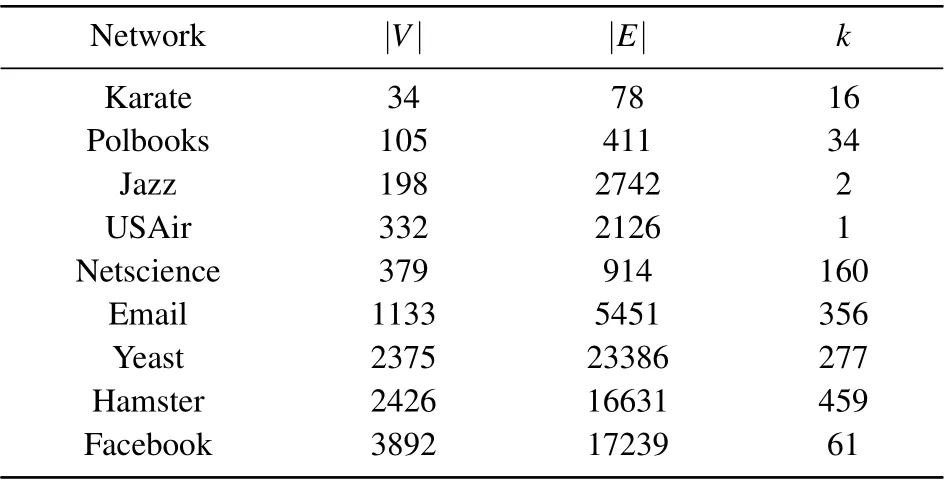
Table 2. The value of parameter k over all networks.
The number of attributes of the network is usually less than the number of vertex. Thus for simplicity,the sorted lists under differentkvalue are obtained via adjustingθ=0.5 andα= 0.5, wherek ∈{1,n/2}. Thekvalue is selected corresponding to the optimal Kendall coefficientτ. Table 2 is demonstrate the final selected value ofkon all networks.Next,we investigate how parameterαandθinfluence the performance of the proposed algorithm. By fixingk, the parameterαandθincrease from 0 and 0.1 to 1 with the gap 0.1,respectively. The variation in the accuracy of VCJG as parameterαandθincrease for four dataset is shown in Fig.1. As can be observed in the picture,the highest values ofτcan be obtained forθ=0.8 andα=0 over the Karate dataset,forθ=0.5 andα=0.1 over the Polblogs dataset, forθ=0.8 andα=0.3 over the Email dataset, and forθ=0.8 andα=0.2 over the Yeast dataset.
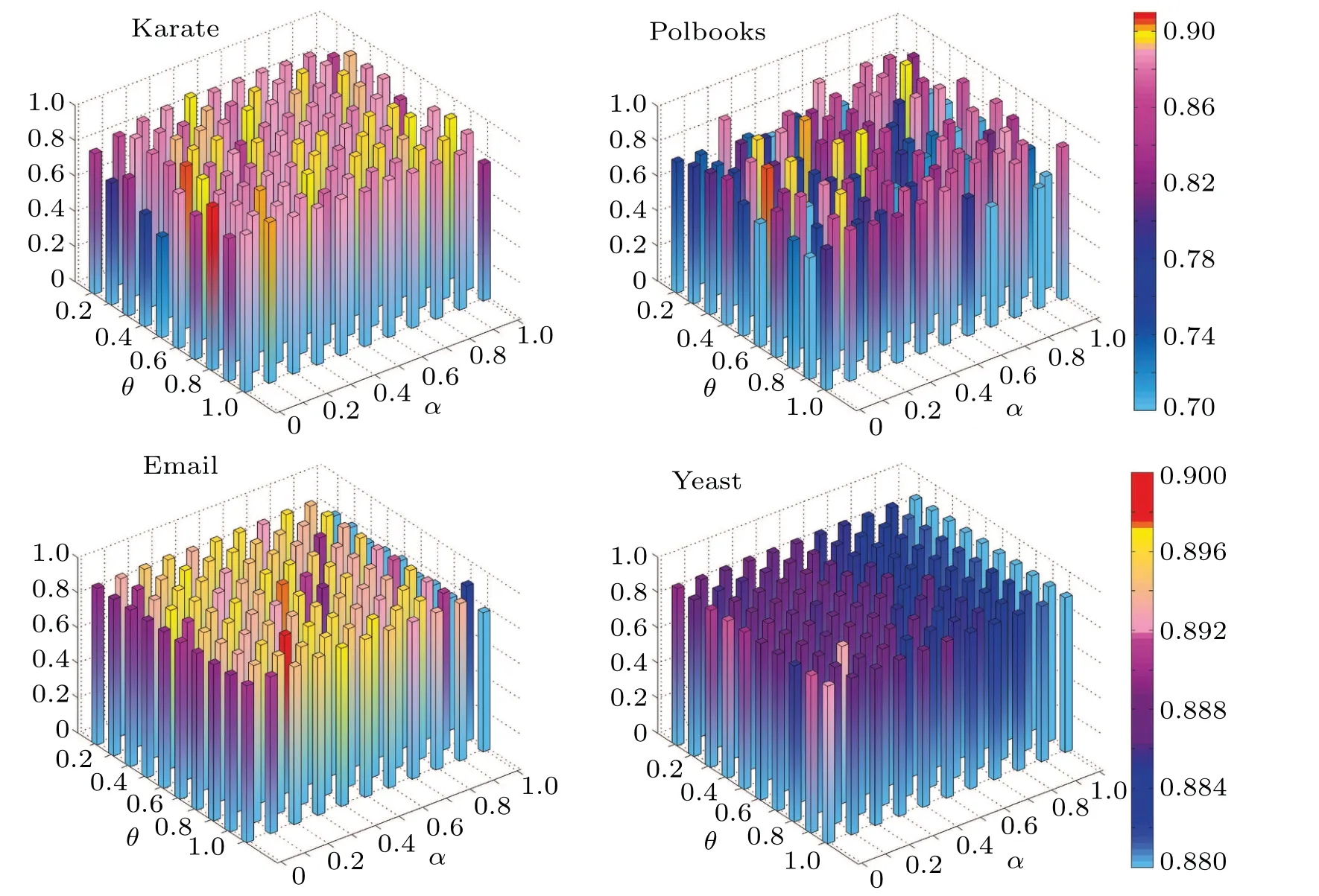
Fig.1. Effect of variation of parameters θ and α on the accuracy of the proposed method based on Kendall’s τ correlation coefficient over the four dataset.
In conclusion,asθ=0.8,VCJG reaches a good balance between thel-order global topology. In the wake of parameterαincreases from 0 to 1, the accuracy of VCJG increases from low to high,and then gradually decreases. The reason is that whenαis small, the attributes of vertex are excessively smoothed to global topology. Whenαis large, the attributes are dominated by local topology,thereby resulting in an undesirable performance.Based on the above results,the extraction of attributes and topology reaches a good balance forθ=0.8 andα=0.2. Thus,these values are considered for the parametersθandαfor remaining experiments.
5.3. Correlation
In order to evaluate the lists ranked by all the centrality indicators, the list ranked by the real diffusion process of the vertices requires obtaining.The standard susceptible-infectedrecovered(SIR)model[42]is adopted to simulate the spreading process on networks and record the diffusion efficiency for every vertex.Every vertex pertains to one of the susceptible state(S),the infected state(I)or the recovered state(R)in the SIR model. Initially, one vertex is set to infected state and other vertices are susceptible vertices. At each step, each infected vertex can infect its susceptible neighbors with probabilityβ,and then can be deleted with probabilityγ. This dynamic process will repeat until there is no infected vertices.
In this paper, the SIR process is repeated 1000 times for each vertex to increase ranking accuracy and the average value of the vertex’s spreading capability is considered as it is importance. The infection probabilityβis set near the infection rate threshold andγ=2β. The infection rate range of each network is shown in the abscissa of Fig.2.
For measure the performance of the centrality algorithms,the Kendall’s coefficientτ[43]is employ to evaluate the correlation between ranking list and the one generated by the SIR model. The Kendall’s correlation coefficientτis defined as

whereτ ∈[-1,+1].zcandzddenote the number of concordant and discordant pairs respectively. The higher the value ofτ,the more accurate the ranking generated by the centrality measure.
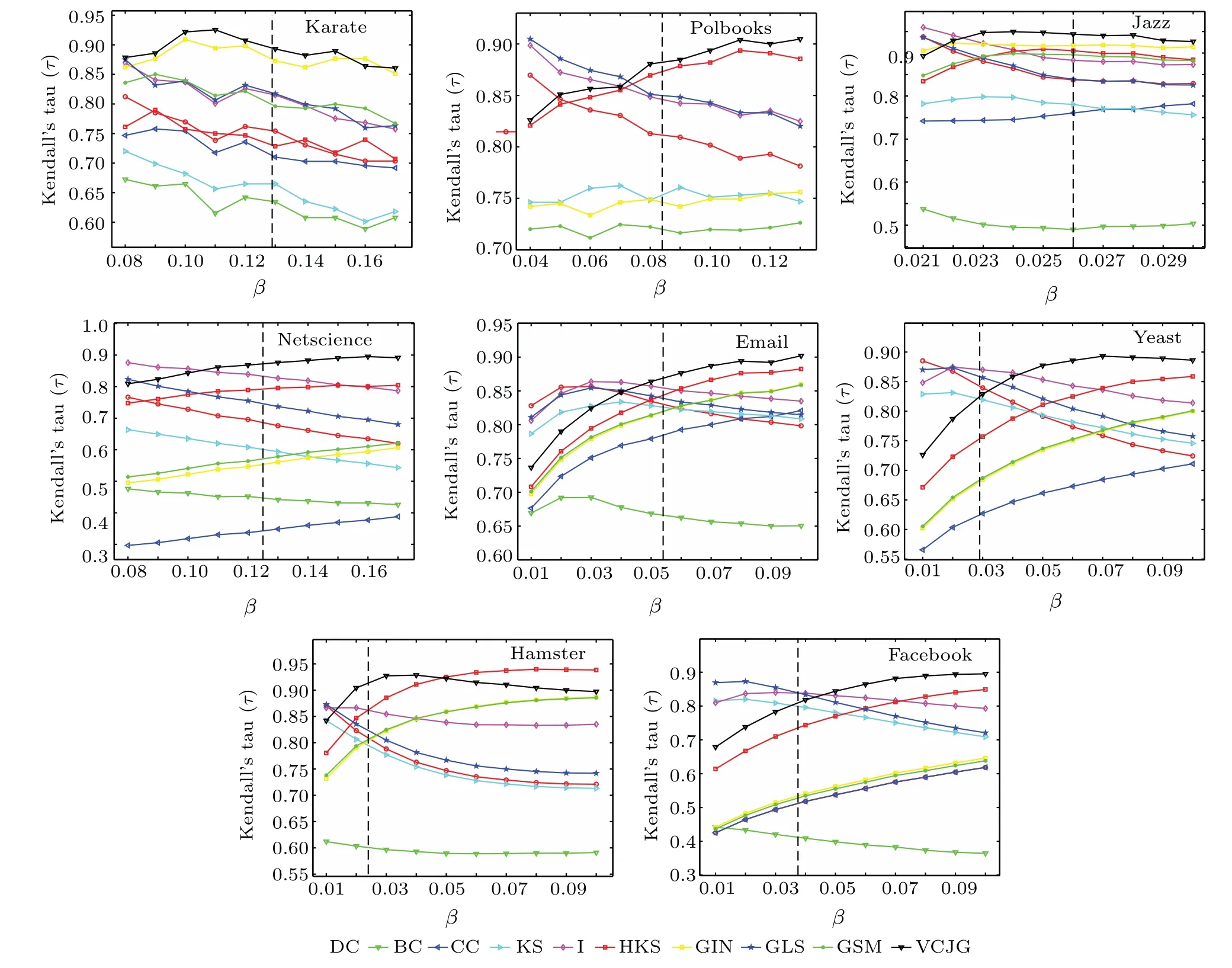
Fig.2. The influence of the change of infection rate on the accuracy of different methods in eight datasets.
The Kendall’s coefficientτin eight real-world networks has been investigated. The calculations,to evaluate the effect of infection probabilityβ, are shown in Fig. 2. The value ofβthin this figure is indicated by dash-dot lines. In Polbooks,Jazz, Netscience, Email, Yeast and Facebook datasets, as the value ofβincreases,especially as it exceedsβth,theτof the proposed method is more highly, and outperforms the other measures. In Karate dataset,after the infection rate threshold,the VCJG’sτshows a downward trend. Although it is lower than the GIN algorithm atβ=0.16,it surpassed it afterwards.In Hamster dataset, afterβ=0.05, theτof VCJG is higher than that of the compared algorithms except HKS. It can be seen that VCJG has different level of “difficulty” in finding influential vertices on different networks. However in most networks, VCJG still shows better performance than current state-of-the-art algorithms.
5.4. Monotonicity
In addition to the above experiments,we also evaluate the monotonicity (M)[44]of ranking for each centrality method.TheMof the indexing method refers to the ability of uniquely identifying vertex from the network. The range ofMlies between[0,1]where 0 means all vertices in the network have the same rank and 1 means unique rank assign to each vertex in the network. Monotonicity is defined as follows:

whereRis the ranking table generated by a centrality measure,Nis the number of levels in sequenceR,Nris the number of vertices with rankrin the ranking tableR.
Table 3 describes the ranking monotonicity of all methods on nine real datasets. It can be seen that monotonicity of VCJG method is lower than most other indexing methods in Jazz dataset. On the other hand,the monotonicity of the proposed methods is the same as HKS,I,GIN,and GSM methods in Email dataset. In the other datasets, the monotonic value of the proposed method is better than all the contrasted algorithms, and is close to 1. The results show that the VCJG method has greater ability to really distinguish the vertices than in the other methods.

Table 3. The M value of different methods in nine networks.
5.5. Accuracy of top-10 vertices ranking
High-ranking vertices in the ranking list are more important than low-ranking vertices,so we require evaluating the accuracy of different methods for identifying high-ranking vertices. Different centrality measures give different lists of the top-10 vertices,depending on how information in the network is considered. The number of same vertices for different measures can show the superiority of different approaches. In the experiment,the top-10 vertex ids are listed to compare the differences in the top-10 vertex results obtained by different measures. And the propagation based on the SIR model to show the superior infection ability of the vertices obtained by the centrality algorithms.
We select indicators from the contrasted algorithms that are less different from the proposed method in the correlation and monotonic experiments for further comparison, such as HKS, GLS and GSM centrality. The top-10 vertices in four datasets are identified and the results are listed in Table 4. A vertex in red color indicates that it not exists in the top-10 lists obtained by the SIR model. For the Polbooks and Email datasets, the distinctness in the number of different vertices between four metrics and the SIR model is relatively small.The distinctness is relatively large in the Jazz dataset because only the top-10 vertices found by VCJG are the same as those generated by SIR. In USAir dataset, the vertices selected by each algorithm are amount to the same those generated by SIR.Therefore,we evaluate the performance of the algorithm from the perspective of vertex arrangement order. The vertices in blue color mean that the order of them are different from the top-10 generated by SIR. For HKS and GSM criteria, there are four vertices in a different order than SIR,while GLS and VCJG methods only have two vertices and the vertices order of VCJG are lower than that of GLS.

Table 4. Vertices ranked by different centrality methods in four datasets.
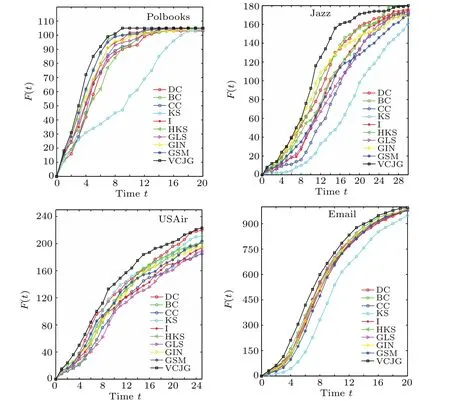
Fig.3. Number of infected vertices for different initial vertices(top-10 vertices)obtained by the ten methods in four networks.
In order to further evaluate whether the vertices obtained by the proposed algorithm have superior infection ability,the SIR model is applied to measure the infection ability of top-10 selected initial vertices. The top-10 vertices obtained by different approaches are used as the initial infected vertices,and the remaining vertices are defined as susceptible vertices. We set the recovery rate in SIR as 0 in order to more easily and accurately count the number of infected vertices. The number of infected verticesF(t)at particular momenttis selected as the infection ability of the initial infected vertices. A higherF(t)indicates that the infection ability of the initial vertices is stronger and that the initial vertices are more importance.
In the experiment, the infection probability of the SIR model on each network is given in column eight of Table 1.Each experiment was carried out independently,and repeated 1000 times under the condition of a specific infection rate.The results are the average of 100 experiments,as shown in Fig.3.Among the four networks, theF(t)of VCJG has little difference with the comparison algorithms in the early stage,but it was higher than other algorithms it keeps up with the growth of time. What we want to point out is that although the list of top 10 vertices obtained by HKS,GLS,and GSM methods in the four networks are slightly different from that for VCJG,the VCJG has a stronger ability for evaluating vertices than the comparison algorithms.
6. Conclusion
In this paper, based on joint nonnegative matrix factorization and graph embedding,we proposed the VCJG centrality to find pivotal vertices in complex networks. It overcomes the shortcomings of existing centrality measures that they cannot completely guarantee completely unrelated among multiple attributes and ignore the heterogeneity between network attributes and structure. This method has good stability and accuracy in different complex networks.
However,VCJG centrality still has some inevitable problems. For instance, there is no better strategy to determine the value of parameterk. And the proposed approach has high time complexity and cannot be applied to large-scale networks.How to increase the speed of VCJG without sacrificing accuracy is a key issue. In future research,we will continue to improve.
Acknowledgement
Project supported by the National Natural Science Foundation of China(Grant Nos.62162040 and 11861045).
杂志排行
Chinese Physics B的其它文章
- LAMOST medium-resolution spectroscopic survey of binarity and exotic star(LAMOST-MRS-B):Observation strategy and target selection
- A novel lattice model integrating the cooperative deviation of density and optimal flux under V2X environment
- Effect of a static pedestrian as an exit obstacle on evacuation
- Chiral lateral optical force near plasmonic ring induced by Laguerre–Gaussian beam
- Adsorption dynamics of double-stranded DNA on a graphene oxide surface with both large unoxidized and oxidized regions
- A polarization mismatched p-GaN/p-Al0.25Ga0.75N/p-GaN structure to improve the hole injection for GaN based micro-LED with secondary etched mesa
