基于用户满意度与排队论的电动汽车充电站选址定容优化

胡丹丹 蔡曙轩

摘 要：以电动汽车使用方的视角下，为尽可能提高用户在获得与接受充电服务过程中的满意度并结合排队论，提出最小化计及耗时与耗电的用户总成本的规划模型；采用遗传算法与贪婪算法相结合的混合启发式算法求解，并通过不同规模的算例证实了算法的有效性，从而优化了采用快速充电模式的充电设施布局。

关键词：电动汽车；充电站；选址优化；排队论；用户满意度

中图分类号：F27 文献标识码：A  doi：10.19311/j.cnki.16723198.2023.03.028

0 引言

城镇化快速发展与人民生活水平的提高让燃油汽车（ICE）基本走进每家每户，加重燃料依赖和空气污染，由此造成能源短缺和环境恶化。于是各国广泛关注新能源，新能源汽车成为其重要应用，其中电动汽车（EV）能有效减少碳排放量。快速充电方式因有效缓解“充电慢”痛点而成为补能首选，快速充电站因提高电动汽车在城市间的机动性而被用户青睐。我国发布了《新能源汽车产业发展规划（2021-2035年）》等一系列政策，车辆保有量逐年激增带来的巨大电力需求突显了充电设施建设的不充分和布局的不合理。因此，科学规划快速充电站的选址，将有效缓解用户的里程焦虑与充电担忧，吸引更多的潜在人群购买电动汽车，逐渐形成为双碳目标提供强大助力的繁荣市场。

经典的设施选址模型分为基于点与基于流的模型，前者有P-Median问题、P-Center问题和覆盖问题等基本模型；后者有Hodgson提出的截流选址模型（FCLM），而后扩展出流续航选址模型（FRLM）等。因电动汽车的充电需求可分“点需求”和“流需求”，故充电设施选址也应基于点或流的模型研究。然而，基于流的选址模型对预测电动汽车保有量的精度要求较高，且在获取尽可能准确的概率分布模型上有难点，更适用于在高速网络上的充电设施部署。对于城市内部的充电设施选址，Anjos等认为使用基于点的模型更适合，且常从成本的角度讨论。Xiao等最小化充电站建设与運营商经营的成本之和，Zhang等研究了不同类型充电设施的建设总成本，杨磊等以用电成本、车辆出行成本、机会成本和惩罚成本之和最小化为目标，Gan等在最大化运营商总利润等。但这些文献没有关注到使用者及其满意度，其结果常难以满足用户需求。

电动汽车充电站的优化研究除选址决策外，还涉及定容问题，即决定所要安装充电桩的数量。任何一类服务设施都有排队系统，学者基于排队论的思想来优化定容决策，其中M/M/c等待制排队模型广泛应用于模拟电动汽车充电站排队系统。Li等最小化车辆到充电站的平均行驶时间和平均等待时间之和，Hu等研究如何通过找到合适的设施位置和相应服务台数，以在承诺的响应时间内最大限度地满足需求。

上述文献多以运营方的角度建模，很少关注使用方的充电体验和满意程度。因此本文提出基于用户满意度、目标函数为最小化包括时间与电力在内的用户总成本的电动汽车快速充电站最佳位置和容量规划模型，用遗传算法结合贪婪算法的混合启发式算法（GgA）求解模型。本研究的创新点主要为：①研究视角新颖，从基于满意度的用户总成本出发；②引入道路弯曲系数计算距离，更符合实际；③考虑用户无不满的充电路程及充电站的服务半径，以衡量车主在充电可获得性上满意度的距离吸引力；④进行一定比例的指派，而非简单的0-1指派。本文其余部分为：第2节做假设和符号说明，并描述问题与建模；第3节介绍遗传嵌套贪婪求解算法，并在第4节的算例验证其有效性；最后第5节给出结语和未来研究方向。

1 问题描述

本文以电动汽车用户的视角，从其满意度出发，基于车辆泊松到达、多服务台负指数服务时间的排队模型，考虑服务范围、预算约束等，尽可能减少顾客为充电所消耗的电量与时间，从而最小化用户总成本。我们进行三方面决策：选址（在哪些位置建电动汽车快充站）、指派（各需求区域车辆指派给哪些充电站及比例）和定容（各建站所安装的快充桩数）。

1.1 假设

（1）将研究区域的连续空间转换为离散空间，并划分成若干个网格，视各中心点为质点及需求点和候选站点；（2）任何一个需求网格里的电动汽车用户可选择去往服务半径范围内的所建充电站中的任何一或几座处充电；（3）假设电动汽车到达充电站的过程形成一个泊松流，且在站排队系统里的服务时间服从负指数分布；（4）虽然车辆的充电时间实际取决于其电池容量与电池荷电状态（SOC），但假定充电桩满足一次车辆充电需求的时间不变。

1.2 符号说明

（1）集合。

N：研究区域内所划分的网格数集；I：所有需求点的集合，其中i∈I；J：全部候选充电站集合，且j∈J；Ji：需求点i在充电站服务半径内可选的候选站点集合（简称筛选后的候选点集），i，Ji=jαdij≤R，j∈J。

（2）参数。

cs：电动汽车快充站的单位建造成本；cp：充电桩的单位购置成本；ce：电力单位成本（即电价）；ct：单位时间成本（即人均单位时薪）；B：总预算；Ns：预建的充电站数；r：用户对与充电站之间距离无不满的充电路程，若超过会有不满；R：充电站的服务半径，车辆在此范围内可来充电；M：极大正常数；Nevi：需求点i所有的电动汽车数量；fc：电动汽车充电频率；Di：需求点i的总充电需求；v：电动汽车平均行驶速度；α：道路非直线系数，取值范围在1.01到1.41之间；β：电动汽车平均行驶一公里的耗电；μ：充电桩平均服务率；dij：需求点i与候选站j的距离；tij：电动汽车从需求点i到候选充电站j的行驶时间；Fij：候选充电站j对需求点i处电动汽车的距离吸引力值。

（3）变量。

Xj：代表是否在候选站点j建站；Yij：表示需求点i处指派给候选站j的电动汽车比例；Zj：表示候选站j安装的充电桩数；λj：代表候选站点j的平均到达率；Wj：表示车辆在充电站j排队等待与接受服务的平均逗留时间。

1.3 模型构建

考虑电动汽车用户满意度，找到Ns个最优充电站位置的选址决策Xj，得到相应的指派方案Yij，然后基于M/M/c排队模型确定各建站最佳充电桩数目的定容决策Zj，从而最小化电动汽车的用户总成本。

（1）目标函数。

Min TUC=ce·∑i∈I∑j∈JαβdijYij+ct·∑j∈J∑i∈ItijYij+INsWjXj=∑i∈I∑j∈Jαβcedij+cttijYij+INs∑j∈JctWjXj（1）

用户总成本（TUC）包括电力成本与时间成本，也可分为路途总成本与逗留总成本。

（2）约束条件。

M=B-csNscp-Ns+1（2）

Di=Nevifc，i∈I（3）

tij=αdijv，i∈I，j∈J（4）

Fij=1120+12cosπR-rαdij-R+r2+π2r<αdij≤r

r<αdij<Rαdij>R，

i∈I，j∈J（5）

M具体指代有限预算下各充电站所能安装的最大充电桩数目；Di由需求点i处Nevi辆电动汽车乘上充电频率fc所得；式（4）用以计算电动汽车从需求点i行驶到候选充电站j所花费的时间。候选充电站j对需求点i处电动汽车的距离吸引力值通过如（5）所示的分段函数计算，当两者的非直线距离不大于用户无不满的充电路程，则距离吸引力值为1；若等于或超过充电站服务半径，则为0；而介于两者间则类似余弦函数，随距离变大而减小。

∑j∈JXj=Ns（6）

∑j∈JiXj≥1，i∈I（7）

Xj=0，1，j∈J（8）

式（6）使选址方案达到预建站数；式（7）确保各需求点i都被覆盖到；Xj在（8）中定义为0-1变量，取1代表在候选站点j建立充电站，取0则不建站。

Yij≤Xj，i∈I，j∈J（9）

αdij「Yij≤R，i∈I，j∈J（10）

Yij=eFijXj∑j∈JieFijXjj∈Ji0   jJi，i∈I（11）

∑j∈JiYij=1，i∈I（12）

0≤Yij≤1，i∈I，j∈J（13）

式（9）指需求點i处电动汽车能指派给候选充电站j的前提是该处有建站；式（10）为充电站的服务半径限制；由（11）得指派方案：当j不属于需求点i筛选后的候选点集jJi时Yij=0，否则建站，再根据Fij计算对应的指派比例；式（12）保证各需求点i的电动汽车的指派比例之和为1；式（13）对指派决策变量Yij进行约束：Yij=0说明需求点i处的电动汽车不指派给候选站j，0<Yij<1表明部分指派给多个充电站，Yij=1时则全指派给j。

∑j∈JcsXj+cpZj≤B（14）

上式表示建站总成本与配桩总成本两方面的总和不得大于总预算B。

Zj≤MXj，j∈J（15）

λj=∑i∈IDiYij，j∈J（16）

λj<μZj，j∈J（17）

Zj∈

，j∈J（18）

式（15）避免对非建站点安装充电桩，且限制建站点的桩数；由式（16）计算候选站点j的平均车辆到达率λj，显然j不建站时λj=0；式（17）认定排队系统到达率要小于其服务率μZj；各候选站点j的充电桩数Zj在（18）定义为非负整数，若不建站为0，否则至少为1。

θjZj=11+μλjZj-1θjZj-1Zj=1Zj>1，j∈J

（19）

Wj=1μ+λjμZj-λj2θj+λjμZj-λj，j∈J（20）

为避免因充电站j的服务强度λjμ过大而导致下溢，Pasternack和Drezner引入参数θj，其计算如（19）；充电站j排队系统属于M/M/Zj模型，车辆到达形成参数为λj的泊松流，Zj个充电桩的服务时间服从参数为μ的负指数分布，平均逗留时间Wj由（20）所得。

最终建起基于用户满意度并结合M/M/c的电动汽车充电站混合整数非线性规划模型：

Min TUC=∑i∈I∑j∈Jαβcedij+cttijYij+INs∑j∈JctWjXj

s.t. 2-20〗

2 求解算法

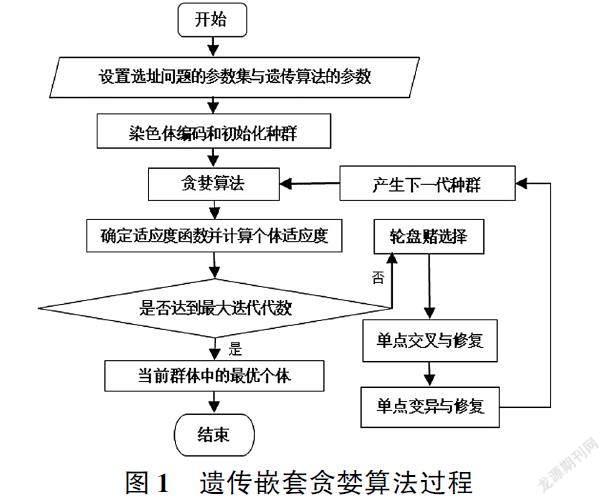
服务设施选址类问题是NP-hard问题，尤其要做位置和容量双决策时更难求解。于是将问题划分为上层做出选址决策的主问题和下层进行定容决策的子问题，再运用启发式算法求解：遗传算法（GA， genetic algorithm）求解充电站位置选择的选址主问题，由贪婪算法（ga，greedy algorithm）来进行各站内充电桩分配的定容次问题，GgA求解的基本流程如图1所示。

2.1 遗传算法求解选址优化问题

模型涉及较多参数和变量，短时间内难以求解，故使用广泛求解选址优化问题的遗传算法。本文采用二进制编码、轮盘赌选择算子、单点交叉变换算子与单点变异算子，但交叉与变异在增加种群多样化的同时可能会带来不可行解，要进行一定的修复。当约束条件不多时，采用罚函数法，将较简单的约束条件并入目标函数；若约束太多则可用如下启发式修复算子：交叉后群体中邻近两个体交叉点上的等位基因不一定发生改变，若该点元素相等则不变，否则由1变0使充电站数少1，就在除交叉点外基因为0的位置里选一个令其为1并确保可行性，如遍历完都不可行则在保证交叉点处元素始终为1下随机生成一条可行的染色体；由0变1的修复同理。变异过后染色体变异点上的基因则必然改变，其修复策略同上。

2.2 贪婪算法求解定容优化问题

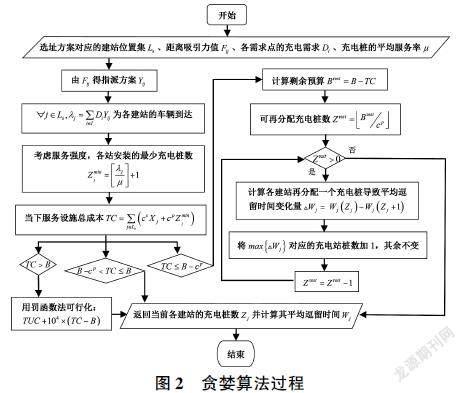
计算非线性方程会大幅度增加时间，逐次确定充电桩数也加大复杂度，如用遗传算法会让收敛速度变慢。给定选址方案后，问题转化为只有定容决策的，可通过贪婪算法得出各设施桩数的精确分配结果。具体采用贪婪算法求解定容优化模型的步骤如图2所示。

图2 贪婪算法过程

3 算例分析

为检验GgA的计算性能，在Matlab R2021a求解不同规模算例。所有算例都在一台CPU为Intel（R） Core（TM） i5-11300H、运行频率为3.10GHz和16GB内存的笔记本电脑上进行。

3.1 随机算例设计

各假设网络均采用网格化法划分成一个个5ⅹ5（单位：公里）的等大网格，并将各网格中心点视为充电需求点，所有需求点都可作为充电站候选点。网格数集N取25、30、35、40、45、50、55、60和65，需求点集I与候选充电站集J也随之确定。各网络下预建站数、总充电需求、投资额有所不同：规定建站数与需求点数的比例不超过1比10，故相应预建站数为2、3、3、4、4、5、5、6和6座；假设各需求点电动汽车总数由指定泊松分布随机生成且平均三天充一次电，可得到充电需求；总预算分别为430、580、630、780、820、980、1050、1200和1250万元。模型其他参数值在表1列出。

种群规模大小分别为30、35、40、50、60、65、75、80、90，染色体长度等同于候选充电站点数，交叉概率各为0.80、0.85、0.85、0.90、0.92、0.92、0.92、0.95、0.95，变异概率均为0.10，最大迭代次数依次为200、250、300、350、400、450、500、550、600。

3.2 算法性能比較

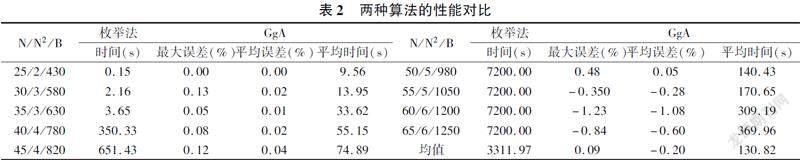
在不同规模算例下，以枚举法为基准对GgA做性能评估。各算例均用该算法随机运行20次；并用枚举法求解，若在7200秒内无法解完则不保证是最优解，再运行两次后取3次中的最优数值为近似最优解。Zh是GgA所得目标函数值，Ze为枚举法2h内所得值，误差定义为：Zh-ZeZe；除误差外还比较它们的计算时间。9个算例所得数据结果记录在表2。

前五种规模算例下枚举法和GgA都得到了最优解，由最大误差不超过0.15%与平均差距在0%～0.04%可见算法稳定和性能良好；后四种算例里枚举法不保证取得最优解，误差显示GgA更可能找到更优解。就求解时间而言，随着网络规模的扩大，枚举法所需计算时间呈指数增长，从第3个算例的3.65秒突增到第四个算例的350.33秒，后四个算例则无法2小时内枚举完；而GgA平均仅需2分多钟求解完，仅小规模时慢于枚举法，表现要更优。

3.3 算法求解性能

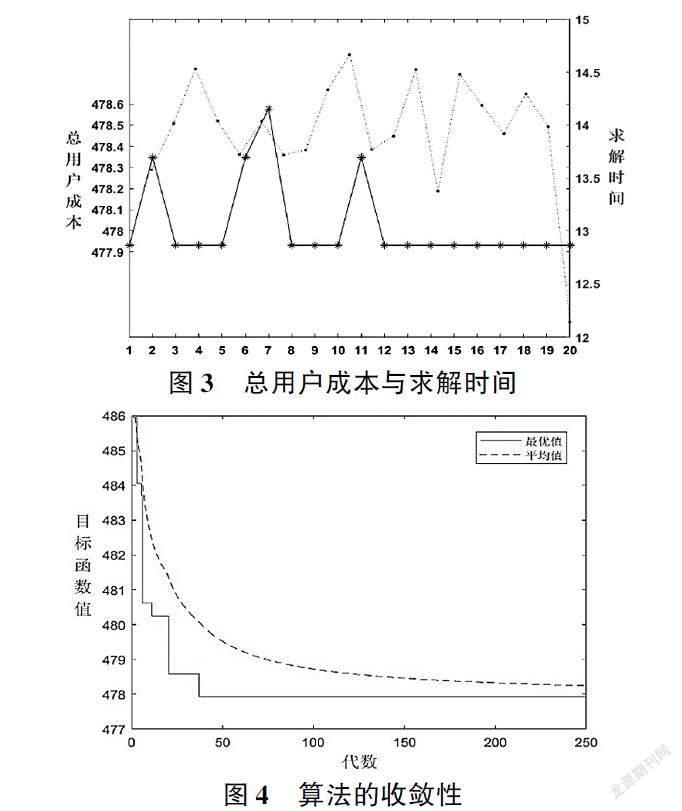
以N=30为例，对GgA进行稳定性、求解时间及收敛性的评估。图3展示随机运行20次程序所得结果，用户总成本只有三种取值，最大波动仅为0.65，可见该算法有良好的稳健性；算法运行时间在12.15～14.67秒，平均时间为13.95秒，很短时间内都可求解问题。取其中目标函数值最优的一次随机实验，记录各代种群中最优个体对应的目标函数值及逐代平均数值，如图4所示。随着初始种群不断遗传迭代，不到50代前搜索到最优结果，随后一直保持水平无波动，表现了算法良好的收敛性能。这点在逐代最好个体平均值上也能体现出。

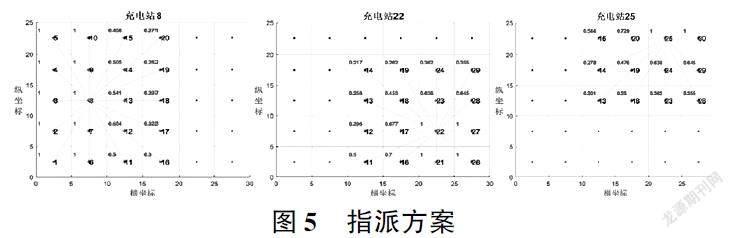
选址定容结果为在点8、22、25建站并对应配置52、35、25台充电桩，具体指派方案如图5所示。点8处所建站给左半部分区域内电动汽车提供充电服务，其中最左边的需求点1到10全部指派给它，而中间部分区域的因距离增大为部分指派；点22的给右下部分领域车辆服务，且最右下的点21、22、27和28处车辆全部指派，其余部分指派；点25的给左上部分区域车辆服务，且最左上的25和30点处的车辆全部指派，其余则部分指派。各建站的充电桩数与其所被指派的需求量相适配，其中充电站8负责提供服务的需求点数显然最多而配置了52个充电桩，而站22的桩数和所满足充电需求要少一些，站25的则要更少。

4 结语

为了改善设施规划不合理、与车辆数比例失衡、分布密度不适配的现状，有必要优化电动汽车充电基础设施的布局。本文以电动汽车使用方为视角，基于用户满意度并结合排队系统，建立了以最小化包括时间成本与电力成本在内的用户总成本为目标函数的电动汽车快速充电站选址定容模型，最大限度地提高电动汽车用户在获得与接受充电服务过程中的满意度；并采用在遗传算法中嵌套贪婪算法而结合成的启发式算法（GgA）在Matlab中求解模型，通过不同规模的算例证实了算法的有效性。

由于充电站选址与定容规划仍有许多需要考虑的因素，本文还存在一些不足之处，未来将在以下几方面进行研究：①只是关于应用快速充电桩的充电站的选址定容规划，可进一步研究采用慢速充电桩的充电站或是换电站的情况；②没有考虑到电网与充电站之间的相互影响，后续可将电网负荷纳入模型之中；③在模型结合车辆轨迹数与流量、POI点数据等估计现实中的充电需求，并将不同类型和电池容量的车辆分开进行讨论。

参考文献

[1]胡大伟，刘成清，胡卉，等.基于低碳视角的两阶段开放式选址路径问题——燃油车与电动车对比[J].系统工程理论与实践，2020，40（12）：32303242.

[2]COLMENARSANTOS A，de PALACIO C，BORGEDIEZ D，et al.Planning Minimum Interurban Fast Charging Infrastructure for Electric Vehicles：Methodology and Application to Spain[J].ENERGIES，2014，7（3）：12071229.

[3]黃柳，胡丹丹.考虑路径偏差和里程焦虑下充/换电站联合布局定容优化[J].物流技术，2021，40（06）：6875.

[4]HAKIMI S L.Network location theory and contingency planning[J].Energy，1983，8（8）：697702.

[5]CHURCH R，REVELLE C.The maximal covering location problem[J].Papers of the Regional Science Association，1974，32（1）：101118.

[6]JOHN HODGSON M.The location of public facilities intermediate to the journey to work[J].European Journal of Operational Research，1981，6（2）：199204.

[7]KUBY M，LINES L，SCHULTZ R，et al.Optimization of hydrogen stations in Florida using the FlowRefueling Location Model[J].International Journal of Hydrogen Energy，2009，34（15）：60456064.

[8]曹小曙，胡培婷，刘丹.电动汽车充电站选址研究进展[J].地理科学进展，2019，38（01）：139152.

[9]郭磊，王克文，文福拴，等.电动汽车充电设施规划研究综述与展望[J].电力科学与技术学报，2019，34（03）：5670.

[10]ANJOS M F，GENDRON B，JOYCEMONIZ M.Increasing electric vehicle adoption through the optimal deployment of fastcharging stations for local and longdistance travel[J].European Journal of Operational Research，2020，285（1）：263278.

[11]XIAO D，AN S，CAI H，et al.An optimization model for electric vehicle charging infrastructure planning considering queuing behavior with finite queue length[J].Journal of Energy Storage，2020，29：101317.

[12]H.Z，Z.H，Z.X，et al.An Integrated Planning Framework for Different Types of PEV Charging Facilities in Urban Area[J].IEEE Transactions on Smart Grid，2016，7（5）：22732284.

[13]杨磊，郝彩霞，唐瑞红.基于电动物流车的充电和换电设施选址模型[J].系统工程理论与实践，2019，39（07）：17811795.

[14]X.G，H.Z，G.H，et al.FastCharging Station Deployment Considering Elastic Demand[J].IEEE Transactions on Transportation Electrification，2020，6（1）：158169.

[15]楊洋，高攀，赵聪泽.城市中电动汽车临时充电站选址和定容模型[J].重庆师范大学学报（自然科学版），2020，37（06）：16.

[16]Y.L，J.L，C.Y C，et al.Growing ;the charging station network for electric vehicles with trajectory data analytics：2015 IEEE 31st International Conference on Data Engineering[C].2015.

[17]HU D D，LIU Z W，HU W S.Congestion Service Facilities Location Problem with Promise of Response Time[J].MATHEMATICAL PROBLEMS IN ENGINEERING，2013，2013.

[18]冯树民，高贺，郭彩香.城市道路网结构形式的评价[J].哈尔滨工业大学学报，2007（10）：16101613.

[19]PASTERNACK B A D Z.Classroom note：A note on&nbsp;calculating steady state results for an m/m/k queuing system when the ratio of the arrival rate to the service rate is large[M].Journal of Applied Mathematics & Decision Sciences，1998：201203.

[20]ZHOU G，ZHU Z，LUO S.Location optimization of electric vehicle charging stations：Based on cost model and genetic algorithm[J].Energy，2022，247：123437.