基于位置信息的DNA 序列特征提取*
2023-02-19深圳大学陈煜元周小安
深圳大学 陈煜元 周小安
DNA 序列的分类是生物信息学的主要研究任务之一,如何提取DNA 序列中的特征是影响分类精度的重要因素。为了更好地保留序列中碱基的信息,本文提出了一种基于碱基距离和相关性的特征提取方法。以H1N1、H5N1、COVID-19 等6 种病毒作为研究对象,将DNA序列转化为特征向量,并用KNN 算法对冠状和非冠状病毒进行分类。实验结果表明该方法能提高分类的准确率。
据估计地球上约有1000 万~1 亿种生物,如此庞大的数据使得生物分类面临着巨大挑战[1],因此DNA 序列的分类成为了人们的研究热点,也是当前生物信息学的主要研究任务之一。特征提取是DNA 序列分类研究中至关重要的一环,旨在最大限度保留原序列数据的基础上将序列转化为数值特征,以挖掘其中所存在的生物规律。随着计算机技术的发展和测序技术的不断进步,碱基的组成和分布信息在DNA 序列特征提取中备受关注[2]。最基本的特征提取方法为K-mers[3],该方法随着k 的增大特征维数呈现指数级的增长,而在训练样本不足的情况下高维数据的研究会带来“过拟合”“维数灾难”等问题[4],故k 的取值不能太大,而特征维数不足可能会丢失序列中的重要信息。此外,K-mers 方法忽略了碱基的距离和排列情况[5]。因此,本文拟提取出基于相同碱基间距离和不同碱基间相关性的特征用于病毒序列分类。该特征提取方法以DNA 序列中碱基的位置为基础,分别记录各碱基出现的位置,再通过合适的数学方法计算出平均距离和相关系数。实验结果表明,新的特征提取方法在KNN 分类器上能取得较好的分类效果。
1 KNN 算法
1.1 KNN 简介
K 近邻(K-Nearest Neighbor)算法简称KNN,是Cover 和Hart 在1968 年时首先提出的。它是一个在理论上较为成熟的算法,也是最常用、最简单的机器学习算法之一。由于和其他分类算法相比没有显示的学习过程,所依据的“多数决定”的思想很容易理解,在多分类问题上表现的比其他分类算法要好,而且计算过程经过优化后能够大幅降低计算次数,因此在分类领域有着广泛的应用[6]。算法的原理是将待分类的样本与训练集的样本逐一计算出距离,按距离从小到大进行排序,然后取出最近的K 个训练样本,这K 个样本中数量较多那一类即为测试样本的类别。
1.2 距离的计算
KNN 计算序列样本之间距离的方法主要有曼哈顿距离、欧式距离和闵可夫斯基距离等,本文采用的是欧式距离法。令训练样本为X,特征的向量表示为(x1,x2,…,xn),测试样本为Y,特征为(y1,y2,…,yn),则它们的欧式距离如式(1)所示:
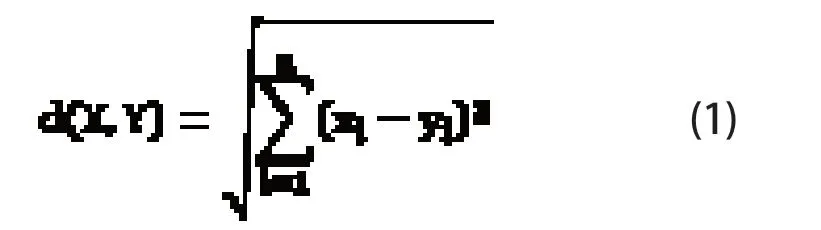
式中n 表示X 和Y 的特征维数,若n=2 相当于计算平面上两点之间的距离,n=3 相当于计算三维空间中两点的距离。上式计算的是一个训练样本和一个测试样本之间的距离,实际的分类问题中往往有m 个训练样本{X1,X2,…,Xm},需分别计算待分类样本与每个训练样本的距离d(Xi,Y)(i=1,2,…,m),从小到大排序后再进行下一步工作。
1.3 K 值的选取
K 值的选取是KNN 算法中至关重要的一环,取值太小容易导致过拟合,太大则会使得分类误差增大。不仅如此,K 值有时能直接影响到分类结果。如图1 所示,假设一个二分类问题,蓝色正方形代表类别A,绿色三角形代表类别B,红色圆形为待分类样本X。若取K=3,即把距离最近的3 个样本作为依据,此时类别B 的个数为2,类别A 的个数为1,此时KNN 会将待分类样本归为类别B;而取K=5 时显然类别A 的个数比类别B 的多,则X 会被归为A 类。
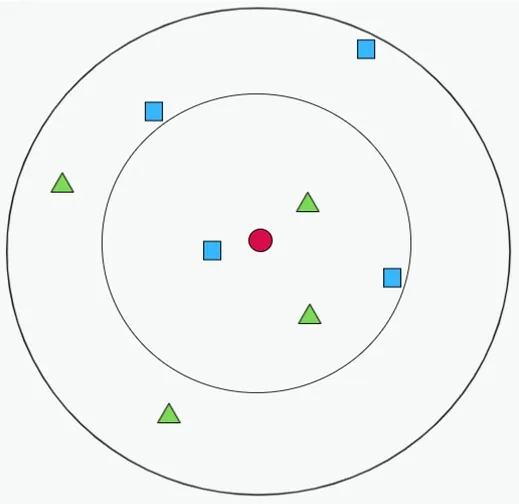
图1 K 近邻算法Fig.1 K-nearest neighbors
为了降低上述情况带来的影响,可以采用距离加权的方式,给每个已知类别的样本赋予权重,其值和训练样本与测试样本之间距离成反比,这样就使得较相似的样本点在分类上具有更高的权重。本文将通过经验法选取合适的K值,即对不同的K 值进行重复实验,得到一个使分类准确率最高的结果。
2 序列特征的提取
2.1 基于碱基频率的特征提取
这是一种比较典型的特征提取方法,即k-mers法,以各碱基或碱基组合在DNA 序列中的频率作为特征。由于碱基的种类有4种,故对于k(k=1,2,3,…)个碱基的组合,共有4k种组合方式。
单碱基有A、T、G、C 4种,在不同DNA 序列甚至同一序列的不同片段中,每种碱基出现的频率也是不相同的。设一条含有m 个碱基的序列,其中碱基n 的个数为c,则碱基n 的频率可记为Pn=c/m。把4 种碱基的频率用向量表示如式(2)所示:

其中Pi(i∈{A,T,G,C})表示碱基i 在序列中出现的频率。
双碱基有AA、AT、AG、AC、TA、TT、TG、TC、GA、GT、GG、GC、CA、CT、CG、CC 共42种,即16种组合方式。实验采用滑动窗口算法对各双碱基的个数进行计算,这样可以降低碱基缺失对实验结果的影响。一条含有m 个碱基的序列,用滑动窗口法得到的双碱基共有m-1个,故双碱基n 的频率可记为Pn=c/(m-1),c为双碱基n 出现的次数。可将双碱基在序列中的频率表示为如下16 维向量:
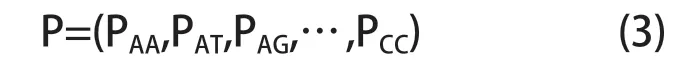
其中Pij(i,j∈{A,T,G,C})表示碱基ij 在序列中出现的频率。
基于三碱基的表示方法共有64 种组合,同样用滑动窗口法计算出各三碱基的频率,将其用如下64 维向量表示:
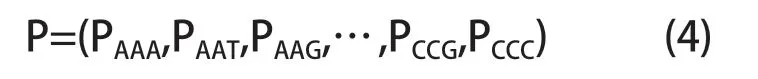
其中Pijk(i,j,k∈{A,T,G,C})表示碱基ijk 在序列中出现的频率。
基于四碱基组合的表示方法共有44即256种,五碱基的共有1024种,随着n 的增大组合方式呈指数型增长。在实际的机器学习算法中,太多的特征会使得计算的时间成本增加,且可能导致过拟合。此外,多个碱基的组合在序列中出现频率较低,故不考虑3 个碱基以上的频率作为特征输入。
上述基于碱基频率的特征提取方法虽然能取得较好的分类效果,但是并不能表达出碱基的位置信息。本文提出一种新的DNA 序列特征提取方法,与k-mers 方法不同的是,新方法在考虑了碱基频率的基础上还包含了序列中碱基的距离和相关性信息。
2.2 基于碱基位置信息的特征提取
2.2.1 基于碱基距离的特征提取
仅用碱基的频率还不足以描述一条DNA 序列,因为两条完全不同的序列可能会出现相同的碱基频率,如以下两条长度为20 个碱基的序列:
序列a:ATCGC GCAGA GATAT CTATA
序列b:GCACA TCAGA TCAGA TATGT
序列a 和序列b 的A、T、G、C 含量完全相同,双碱基含量和三碱基含量如AT、AG、TC、GCA、TAT等也有相同或相似之处,但这却是截然不同的两条序列。因此,为了使得分类更加准确,可用一种新的基于碱基距离的特征表示方法,即碱基(或碱基组合)之间的平均距离来描述一条序列。设有一条长度为m 的DNA 序列S=s1,s2,...sm,用Cn表示碱基n(n∈{A,T,G,C})的个数,Lni来表示碱基n 在序列中第i 次(i=1,2,…,Cn)出现的位置,则相邻碱基n 之间的距离Dnj=Lnj+1-Lnj(j=1,2,…,Cn-1),序列中碱基n 的平均距离为:

以序列a为例,碱基A的个数CA=7,位置分别为LA1=1,LA2=8,LA3=10,LA4=12,LA5=14,LA6=18,LA7=20,相邻两个碱基A 之间的距离DA1=7,DA2=2,DA3=2,DA4=2,DA5=4,DA6=2,可算出其平均距离:
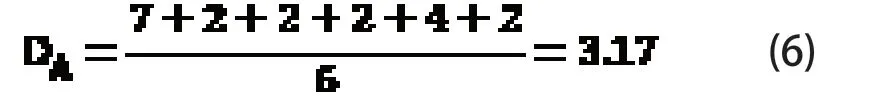
同理碱基T 分别位于第2,13,15,17,19处,故碱基T 的平均距离DT=3.4;用该方法算出碱基G 和碱基C的平均距离分别为DG=2.33,DC=4.33。对于序列b 也用此法计算得:DA’=2.3,DT’=3.5,DG’=6,DC’=3.33,即:
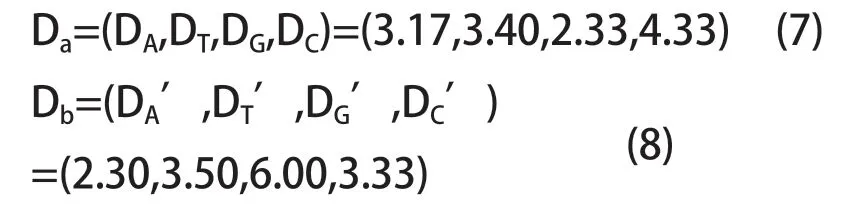
其中Da、Db分别表示序列a 和序列b 中碱基A、T、G、C 的平均距离向量。可看出在单碱基含量相同的情况下,碱基之间的平均距离可能会有较大的差异。
对双碱基的平均距离和单碱基的计算方法类似,碱基组合的位置以第一个碱基为准。例如要计算序列a 中碱基组合AT 的平均距离,可找出4 个AT,其中碱基A 的位置分别为1、12、14、18,故AT 的平均距离DAT=5.67;同理序列b 中AT 的平均距离DAT’=4。碱基AT 在序列a 和序列b 中含量相同(都是4 个),平均距离却有所差异,这正说明了我们不能只关注序列中碱基的含量而忽略了碱基的距离信息。
2.2.2 基于碱基相关性的特征提取
序列中不同碱基之间的相关关系也是区分不同种类生物的重要特征之一,将碱基n 的位置分布记作Sn(x)(x=1,2,…,m),其定义为:
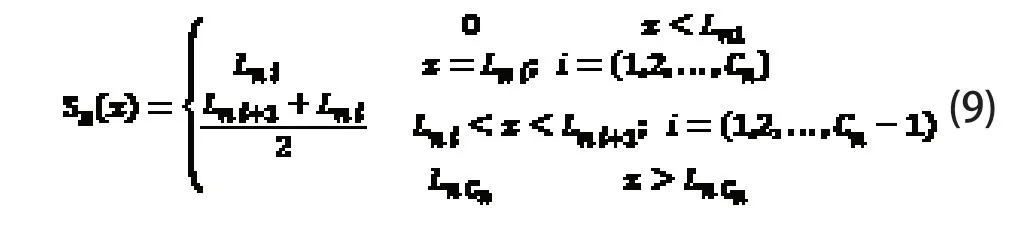
式中Lni表示碱基n 在DNA 序列中第i 次出现的位置,Cn表示碱基n 的个数。在碱基n 第一次出现之前,位置记为0;两个碱基n 之间的位置记为它们的平均值;最后一个碱基n 之后的位置都记为最后一个碱基n 出现的位置。
以序列a 为例,CT=5,LT1=2,LT2=13,LT3=15,LT4=17,LT5=19,故ST(2)=2,ST(13)=13,ST(15)=15,ST(17)=17,ST(19)=19;第一个T 出现之前,ST(1)=0;最后一个T 之后,ST(20)=19;两个T 之间,ST(3)=ST(4)=…=ST(12)=(2+13)/2=7.5,ST(14)=(13+15)/2=14,ST(16)=(15+17)/2=16,ST(18)=(17+19)/2=18,即碱基T 在序列a 中的位置分布为:

同理计算出碱基G 在序列a 中的位置分布为:
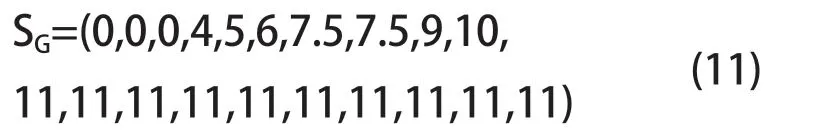
为体现序列中两种不同碱基的相关程度并用数值表示出来,可用皮尔森相关系数来计算,定义是两个变量之间的协方差和标准差的商:
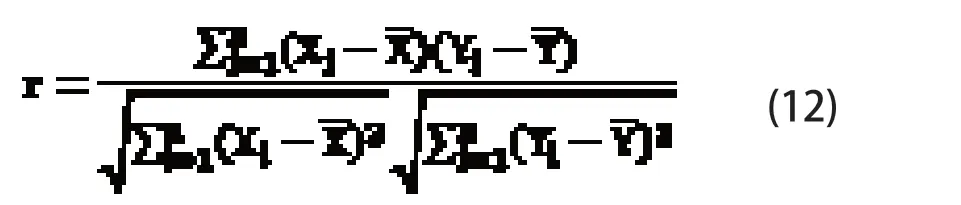
综上,本文提取出DNA 序列中基于碱基频率、碱基间的距离和相关性的110 维特征向量:
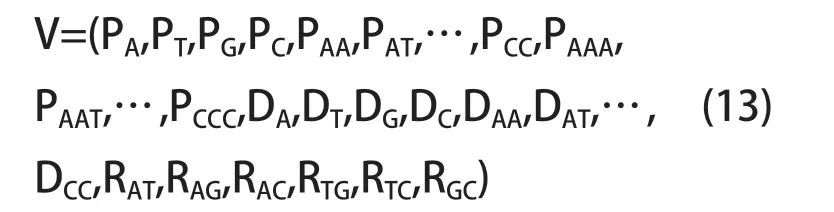
将其作为KNN 算法中的特征输入,对病毒序列进行分类研究。
3 实验结果分析
本文采用的实验数据均来源于美国国家生物技术信息中心(NCBI)。从NCBI 网站上下载6 种不同病毒(H1N1,H5N1,H7N9,SARS,MERS,COVID-19)的DNA 序列,前3 种为非冠状病毒,后3 种为冠状病毒。每种病毒各取50 组序列,总共300组,其中150 组的类别为“冠状”,另外150 组类别为“非冠状”,每组序列包含240 个碱基。用Python 中的scikit-learn 模块对序列进行二分类,评估指标为分类准确率(Accuracy),即正确分类的序列个数占总序列个数的比例。
首先用KNN 算法进行两轮实验,第一轮实验的数据是碱基的频率特征,即序列中单碱基、双碱基和三碱基的频率,共84 维数据。第二轮实验的数据是在第一轮实验的基础上增加碱基的距离和相关性特征,共110 维数据。两轮实验分别测试不同K 值下的分类准确率,结果如表1 所示。
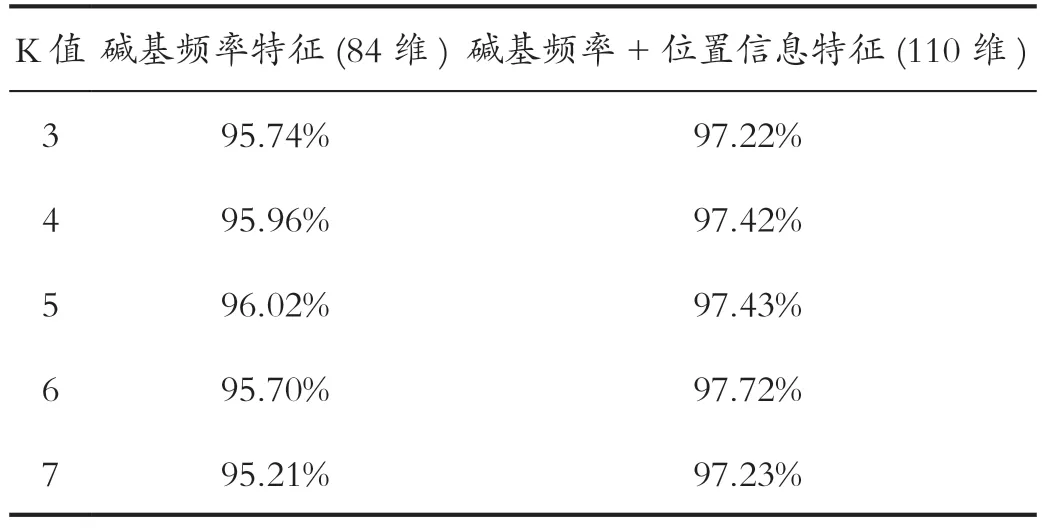
表1 两种特征提取方法的分类准确率Tab.1 Classification accuracy of the two feature extraction methods
由表1 可知,在K 值为3~7 的情况下,分类准确率呈抛物线趋势,先增后减。在仅采用碱基频率特征的算法中,K=5 时分类准确率最高,为96.02%,K=4 次之;增加了碱基距离和相关性特征的实验中,K=6 时分类准确率最高,为97.72%,K=5 次之。无论K 的取值为多大,增加了距离特征之后的分类模型都是更有效的,准确率均提高1%~2%左右。
上述实验中训练样本与测试样本的比例为7:3,即210 组训练序列,90 组测试序列。考虑到测试样本的归类是以训练样本的类别为依据的,此比例可能会影响分类结果。本文在训练样本数量应大于测试样本数量的原则上,适当调整了比例,以碱基的频率和位置信息的110维特征作为输入进行了重复实验,结果如表2 所示。
由表2 可知,训练集与测试集比例为8:2 且K=6时,训练集与测试集比例为9:1 且K=5 或K=6时,分类的准确率能达到98%以上。比例为8:2 且K 的取值为5 时的准确率非常接近98%,这正说明K 的取值偏大或偏小都会使得分类效果降低,在K=5 和K=6 时可达到较高的准确率。此外,无论K 的取值为多少,分类准确率都会随着训练集和测试集比例的增加而提高,即训练样本较多时模型能更加高效地学习。综上,将采用训练集与测试集比例为9:1,K=6 的KNN 模型进行序列的分类,此时准确率最高,为98.47%。
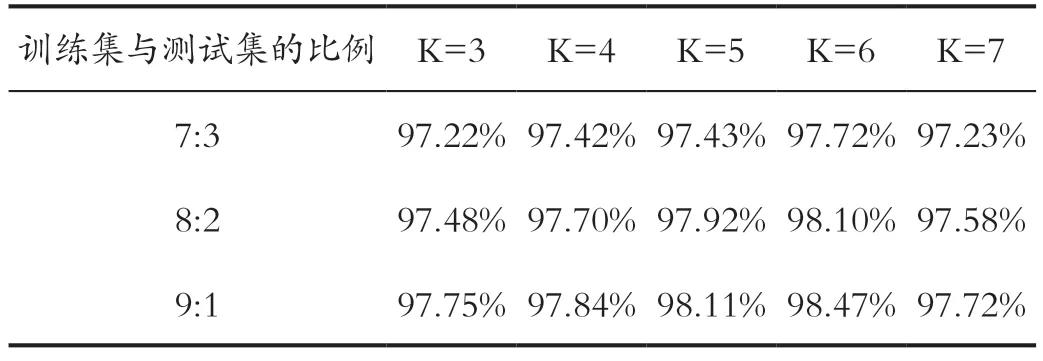
表2 不同比例下的分类准确率Tab.2 Classification accuracy of different proportions
4 结语
本文阐述了DNA 序列中碱基位置信息的重要性,提出一种基于碱基之间的距离和相关性特征表示方法,将其运用于6 种病毒序列的特征提取,并利用KNN 算法进行分类,实验结果表明该特征提取方法能提高分类准确率。这种方法提取的特征向量维数较高,因此更适用于多个DNA 序列的分类研究。
引用
[1] 窦向梅,肖晖,黄大卫.DNA分类概述[J].生物学通报,2008,43(6):23-25.
[2] 刘福乐.DNA、RNA和蛋白质序列特征提取方法研究及应用[D].哈尔滨:哈尔滨工业大学,2015.
[3] Shobhit Gupta,Jonathan Dennis,Robert E Thurman,et al.Predicting Human Nucleosome Occupancy from Primary Sequence[J].PLoS Computational Biology,2008,4(8): e1000134.
[4] 李郅琴.特征选择方法综述[J].计算机工程与应用,2019,55 (24):10-11.
[5] 韩轶平,余杭,刘威,等.DNA序列的分类[J].数学的实践与汄识,2001(1):38-45.
[6] 皮亚宸.K近邻分类算法的应用研究[J].通讯世界,2019,26(1): 286-287.
