基于Lomb-Scargle 算法的激光扫频干涉非线性校正方法*

龙康 孔明 刘璐 刘维 华杭波 许新科

(中国计量大学计量测试工程学院,杭州 310018)

激光扫频干涉测量技术因其精度高、抗干扰能力强等优势成为研究热点.而激光器调频的非线性问题一直是影响测量精度的关键因素,非线性带来的直观结果就是拍信号的频谱严重展宽,造成测距精度下降.为解决该问题,本文提出了一种基于Lomb-Scargle 算法的非线性校正方法,搭建了具有辅助干涉仪的激光扫频干涉测量系统,通过对辅助路拍信号进行希尔伯特变换提取相位,再基于提取到的相位信息生成一个新的时间序列,结合Lomb-Scargle 算法,将非线性校正与拍信号频率计算同时进行.作为验证,对于0.5—1.3 m 范围内的目标进行了测量,最大误差为14 µm.区别于传统频率采样法校正原理,本文提出的校正方法并不是以辅助路的拍信号对测量路进行重采样,所以无需满足辅助干涉仪光程差大于测量路光程差两倍的条件,因而可为增大测距量程提供一种思路.

1 引言

激光扫频干涉测量技术因其精度高、可进行非合作目标测量等优势受到了广泛研究[1−6].然而激光器调频非线性问题的存在直接影响着测量精度,理想状态下激光器输出信号的频率随时间严格线性变化,但在实际工作中由于激光器受到温度、电流以及调谐特性的影响,线性调频难以实现,从而造成拍频频谱展宽,最终增大测量结果的误差.

为了解决激光扫频干涉测距的非线性问题,常见的校正方法可以分为闭环校正和开环校正法.闭环校正一般是基于光电锁相环的负反馈电路,将拍信号与给定的参考信号对比,利用频率差或者相位差作为反馈量进行校正.1996 年,日本的Iiyama等[7]采用了参考干涉仪和电相位比较器设计了激光测距系统,在反射测量中约16 cm 处测距分辨率从原来的12 mm 提高到1.3 mm.2009 年,Roos等[8]基于光纤自外差技术搭建了超宽带激光频率啁啾线性化的闭环锁相测量系统,在1.5 m 范围内,测距精度提升至31 µm.Behroozpour等[9]于2016 年提出了基于芯片级光电锁相环反馈技术的调频连续波测距系统,实现了1.4 m 范围内8 µm 的测量精度.基于反馈系统的校正方法可以实现对非线性的实时校正,而且精度较高,但是该方法也存在锁频范围有限、硬件要求十分高等缺陷.对比而言,开环校正的成本较小,实施起来更为简便.给激光器输入特定的非线性调制波形是一种常见的预校正手段,在此过程,采用合适的迭代算法也能取得一定的效果[10,11].此外,重采样技术也是解决非线性的典型方法之一,其中基于频率采样法的重采样技术结构简单,实用性很高[12−14].1993 年,Glombitza 和Brinkmeyer[15]提出了用已知光程差的辅助干涉仪对测量路的干涉信号进行等光频采样,测量分辨率达到了50 µm.Ahn等[16]于2005年提出了基于希尔伯特(Hilbert)变换的补偿法,利用辅助路的希尔伯特变换来估计光源的瞬时相位和频率,然后通过插值法对测量路拍信号进行重采样,进而校正非线性的干扰.2018 年,Shi等[17]提出了带有两个辅助干涉仪的测距系统,在5.8 m处的测量误差在20 µm 以内.

但传统的频率采样法受到奈奎斯特采样定理的限制,加上激光发射与接收需要经过往返距离,这就意味着频率采样法要满足被测目标对应的距离不能超过辅助干涉仪光程差的1/4,限制了测距范围[18].针对此问题,2019 年Bao[19]等提出了一种等光频细分重采样法,以辅助路拍信号的峰谷作为特征点将信号细分成多个等时间间隔段,再对测量路信号进行重采样,实验在4.3 m 范围内的测量标准差为22.23 µm.2021 年Jiang等[20]利用倍频器来缩短辅助干涉仪的光程差,将带有两个乘法器的四倍频电路板添加到测距系统中,对目标距离6.4 m 处的测量实现了9.4 µm 的标准差,但是该方案引入了额外的硬件电路,增加了系统的复杂度.

本文提出了一种基于Lomb-Scargle(LS)算法的开环非线性校正方法,在校正非线性的同时得到拍信号的精确频率.利用基于辅助路拍信号相位变化的时间序列,与LS 算法结合达到了较好的校正效果.另一方面,区别于传统的频率采样法,LS 算法并不需要使用辅助信号对测量信号进行重采样,因此不需要满足辅助路的光程差大于测量路的两倍,理论上就可以避免传统频率采样法测距量程受限于辅助干涉仪光程差的缺陷.

2 原理

2.1 激光扫频干涉测距系统模型

激光扫频干涉测距系统模型如图1 所示,激光器受三角波信号的调制,输出的信号经耦合器1 被分为两部分,其中99%的能量进入测量信号路,1%的能量进入辅助信号路.测量路的信号又由耦合器2 分为两部分,99%的能量经过环形器再通过镜头出射至目标,被反射后原路返回,与另一部分1%的本振信号在平衡探测器1 中干涉形成测量路差拍信号.辅助信号路由耦合器3 分为50∶50 两部分,通过不等臂长的光纤Mach-Zehnder 干涉仪,在平衡探测器2 上形成辅助干涉仪差拍信号.

图1 激光扫频干涉测距系统示意图Fig.1.Schematic diagram of the laser scanning interference ranging system.

在理想状态下激光器输出信号的频率随时间线性变化,如图2 所示.由于测量光和本振光的传输路径不同,所以会产生相应的时延τ,从而产生瞬时频率差fa,这个瞬时频率差即为拍信号,最终被探测器捕获.图中B为调频带宽,T为调频周期,f0为调频初始频率.

图2 理想情况下拍信号形成示意图Fig.2.Schematic diagram of beat signal formation under ideal conditions.

但在实际情况中,由于非线性的存在,调频激光器发出的激光瞬时频率随时间并不是线性变化的,可以表示为

其中fε(t)为激光器输出的非线性项,kB/T为调频斜率,t为调频时间.则辅助路拍信号为

其中U1为幅值,τ1Rjnj/c为辅助干涉仪的时延,Rj为辅助干涉仪的臂长差,nj为光纤折射率,c为光在真空中的传播速度.同理可得测量路拍信号:

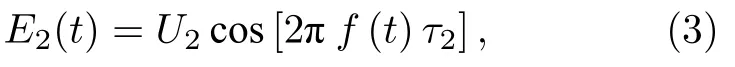
其中U2幅值,τ22Rn/c为测量路的时延,R为激光在空气中的单向传播距离,n为测量光路的空气折射率.

2.2 LS 算法原理

对于非均匀采样时间序列的功率谱分析,LS法具有较好的效果.该算法是基于离散傅里叶变换原理,通过对数据用最小二乘法进行模型曲线拟合,根据均方根误差来判断数据隐含的周期变化趋势和猜想模型的符合度,不仅能从时间序列中提取出较弱周期信号,而且能在一定程度上减少非均匀时间列的虚假信号的产生[21].

在激光扫频干涉测距系统中,对于固定采样频率所采集的信号,在时间上是均匀的,但是由于调频非线性的存在,对这种时间上均匀的信号直接做快速傅里叶变化(fast Fourier transform,FFT)并不能很好地反映出拍信号的频率值.为了充分发挥LS 算法在对非均匀数据序列频谱估计上的优势,本文利用辅助路拍信号的相位变化来构造一个新的非均匀时间序列,结合LS 算法对非线性进行校正.LS 法周期图功率谱可以表示为[22,23]

其中N为信号点数;ω为待估计的角频率;E,σˆ2分别为样本均值和样本方差.τ满足

其中ti是采样时刻.将ti进行如下变换:

其中 Δt表示采样时间段,pi是辅助路拍信号中第i个序列所对应的相位.转换后新的ti便携带了辅助路信号的相位信息.将E1(ti)和E2(ti)分别代入(4)式,可以得到校正非线性后的拍频频率f1′和f2′.则最终的目标距离:

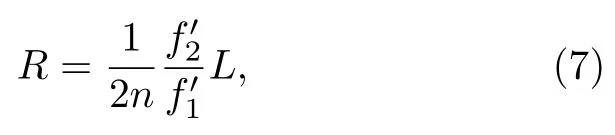
其中LRjnj为预先标定的辅助干涉仪的光程差.

3 实验与结果

实验过程示意图如图3 所示,设置目标为平面反射镜,将其贴在三坐标测量机探头上,实验过程中始终保持单轴测量导轨与光路共轴.初始时刻出射镜头离目标的距离R约为0.5 m,实验过程中往后多次移动一定的距离(ΔR)进行测量.分布式反馈(DFB)激光器驱动信号为三角波,调频带宽为43.6 GHz,光源波长为1550 nm,激光器的扫频频率为1 kHz,采集卡的采样频率为40 MHz.

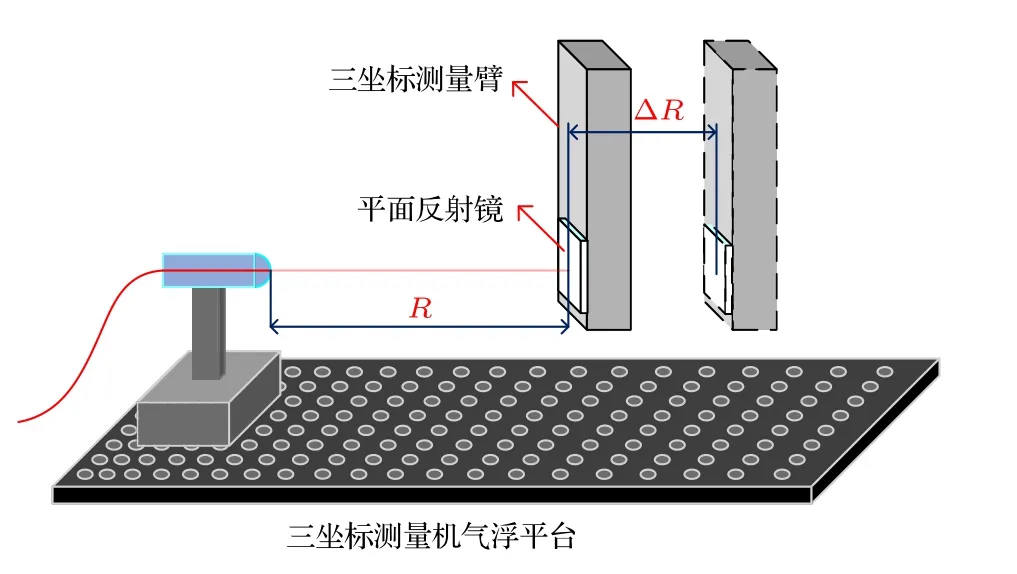
图3 测量实验过程示意图Fig.3.Schematic diagram of the measurement experiment process.

如图4(a)所示,未进行非线性校正前,对拍信号进行FFT 后的频谱发生了严重的展宽,导致信号中心频率提取误差较大;图4(b)展示了Hilbert变换后相位曲线与理想线性直线存在着明显的偏差;图4(c)为时频曲线局部图,可以看出频率并非稳定在一个恒定值,以上都体现了激光器调频非线性带来的影响.

图4 激光调频非线性对拍信号的影响(a)FFT 变化得到的频谱图;(b)相位偏差;(c)时频曲线局部图Fig.4.Effect of laser scanning nonlinearity on the beat signal:(a)Spectrogram obtained by FFT variation;(b)phase deviation;(c)partial diagram of time-frequency curve.

在进行LS 法校正前,利用辅助干涉仪信号的相位变化趋势来引导(5)式中的时间序列.对辅助干涉光路拍信号进行Hilbert 变换后的结果如图5(a)所示,该图为局部折叠相位图,进一步对相位解包裹后如图5(b).

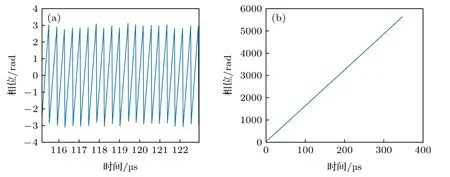
图5 希尔伯特变换提取相位(a)局部折叠相位;(b)解包裹后相位Fig.5.Hilbert transform to extract phase:(a)Locally folded phase;(b)phase after unwrapping.

将解包裹后的相位pi和采样时间段Δt代入(6)式中,得到一个新的时间序列ti,该时间序列携带了辅助干涉信号的相位信息.将转换后的ti代入(4)式并结合(2)式和(3)式,便可得到辅助路和测量路的LS 谱,图6 给出了采用LS 算法在引入新的时间序列前后的LS 谱对比图.

由图6 可以看出,在时间序列转换前LS 谱有明显的展宽,这将导致拍信号频率提取存在很大的误差.将转换后的时间序列代入LS 算法中进行校正,频谱的展宽问题得到了明显的改善,能够准确提取出拍信号的频率值.

将图6(b)和(d)所得的频率值代入(7)式中,便可得到目标的绝对距离.实验标定的辅助干涉仪的光程差约为22 m,测量范围约为0.5 m(初始距离)至1.3 m,多次往远离初始位置的方向移动不同的距离ΔR,并采集了18 组实验数据.对于同一条件下相同的装置和数据样本,分别用LS 算法与经典的频率采样法[11]进行实验,计算出的距离值与海克斯康高精度三坐标测量机(Global 09.15.08)的相对位移量进行比对,该三坐标测量机的示值误差为1.2 µm,以其位移距离作为约定真值,本文所搭建测距系统的绝对误差分布如图7所示.

图6 引入新的时间序列前后LS 谱对比图(a)辅助路引入时间序列前;(b)辅助路引入时间序列后;(c)测量路引入时间序列前;(d)测量路引入时间序列后Fig.6.Comparison of LS spectra before and after the introduction of the new time series:(a)Auxiliary path before introduction of time series;(b)auxiliary path after introduction of time series;(c)measurement path before introduction of time series;(d)measurement path after introduction of time series.

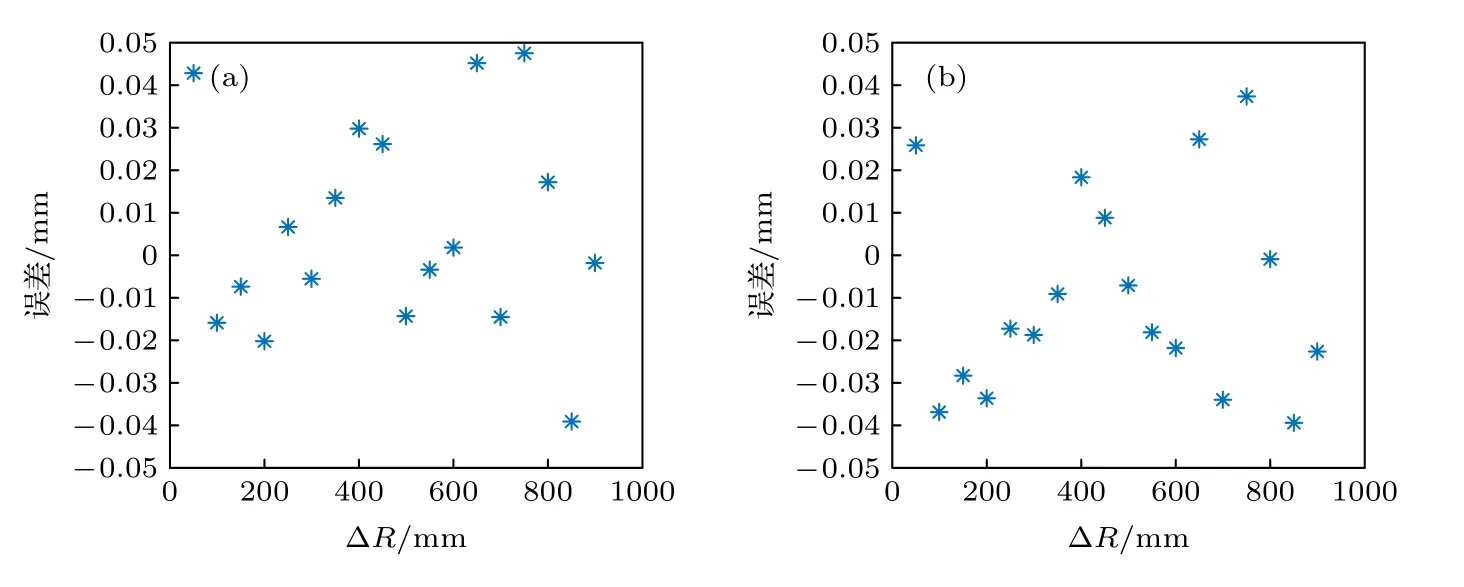
图7 测距误差(a)频率采样法;(b)LS法Fig.7.Distance measurement error:(a)Frequency sampling method;(b)LS method.

由图7 可知,在辅助干涉仪光纤较长时,LS 法和频率采样法的精度从整体上来看差别并不是很大,频率采样法在最大误差处接近50 µm,而LS法在40 µm 以内.然而,LS 法的主要优势不在于此,在使用频率采样法校正时,受奈奎斯特采样频率的限制,其辅助干涉仪的光程差必须要大于测量路光程差的两倍.这就说明在辅助干涉仪长度一定时,系统的测距量程受到了限制,而LS 法并不需要使用辅助信号对测量信号进行重采样,从根本上避免了量程受限的问题.

为了验证上述结论,实验搭建了光程差约为8 m 的辅助干涉仪.需要说明的是,虽然实验过程中测量目标离镜头最远距离约为1.3 m,但是由于在实际装置中测量路到镜头之间也是有一定长度的光纤,加上这段光程以后,测量路光程差的两倍就远大于8 m,所以在这种情况下,频率采样法就不再适用,但是LS 法依旧能表现出较好的精度,表1 是LS 法计算的误差结果.

由表1 可知,在频率采样法不适用时,所采集的5 组数据经LS 法校正后的最大误差为14 µm,相对于频率采样法而言,在辅助干涉仪光程差一定的情况下,LS 法能够在校正非线性的同时扩展系统的量程.此外,对比图7(b),可以看出在辅助干涉仪光程差变短后,系统的误差减小,一方面是对于较短光程差的辅助干涉仪而言,低通滤波器的带宽可以设置得更小,这样就能更好地抑制高频噪声的干扰,从而提高测距精度.另一方面,辅助干涉仪光程差、测量目标距离和系统测量误差之间是存在一定关联性的,当辅助干涉仪光程差越接近于测量目标距离时,目标信号上的有效线性相位噪声越小[24],8 m 的辅助干涉仪光程差相比于22 m 更接近于测量目标的距离(1.3 m),因此受噪声影响程度相对较小.可以看出,在同一实验环境下,由位移台自身引入的误差以及环境振动引入的误差并非主要误差来源,光纤内部的噪声干扰对系统的测距误差起到了主导性的作用,进一步减小噪声带来的干扰是提高精度的关键所在.

表1 频率采样法不适用情况下LS 法测距的绝对误差Table 1.Ranging error of Lomb algorithm when frequency sampling method is not applicable.

4 结论

本文提出了一种基于Lomb-Scargle 算法的非线性校正方法,利用辅助干涉仪的相位信息变化生成了一个新的非均匀时间序列,借助LS 算法将调频非线性校正和拍信号频率的提取一步到位.在辅助干涉仪光程满足测量路光程2 倍的情况下,和频率采样法进行了误差对比实验,实验结果表明,在测量目标的范围为0.5—1.3 m 时,本文提出的校正算法最大误差更小,实验所测量的18 组数据中最大误差在40 µm 以内;在频率采样法失效的情况下,LS 算法对非线性的校正也起到较好的效果,最大误差为14 µm.这也说明了LS 法并不需要满足辅助干涉仪光程差大于测量路光程差2 倍的条件,在校正非线性的同时对扩展系统的测距量程起到了较好的效果.