面向纯相位型全息显示的自适应混合约束迭代算法*

高乾程 何泽浩 刘珂瑄 韩超† 曹良才‡

1) (安徽工程大学,高端装备先进感知与智能控制教育部重点实验室,芜湖 241000)

2) (清华大学精密仪器系,精密测试技术及仪器国家重点实验室,北京 100084)

纯相位型计算全息图舍弃全息面上的振幅信息,降低了全息显示的图像质量.迭代法通过多次正、逆向的波前传播计算,优化了纯相位型计算全息图的相位轮廓,提升了全息再现的图像质量.然而,传统迭代法可能存在迭代发散、收敛速度偏慢以及再现质量受限等问题.本文提出了一种基于角谱传播模型的自适应混合约束迭代算法,通过在迭代中加入自适应的反馈机制和频带约束策略,增加了迭代优化的自由度,提升了迭代的收敛性和全息再现的图像质量.仿真和实验结果表明,提出的算法能够在较短的计算时间内获得更高重建质量的纯相位型计算全息图,对于高质量的全息显示具有重要应用价值.

1 引言

真实世界中的景物通常是具有深度信息的三维物体[1].然而,传统显示技术仅能呈现二维平面图像,深度信息的缺失限制了显示画面的真实性[2].探索三维呈现方式、提升画面展示的真实性,是显示技术的重要发展方向[3].全息三维显示提供了人眼可以感知的所有种类的深度线索[4],是三维内容的理想呈现方式,近年来受到广泛关注[5].最早出现的光学全息显示技术使用相干条纹实现三维场景的记录和再现[6],对记录介质、光学器件和实验系统的要求较为严格[7],且多数情况下只能实现静态场景的三维显示[8].伴随着计算机技术发展而产生的计算全息显示技术使用数值计算实现了相干条纹的获取[9],使用空间光调制器(spatial light modulator,SLM)实现了条纹的加载和重建[10],极大地降低了全息显示的实现难度[11].同时,可刷新SLM 的快速发展[12],为动态三维全息显示的实现奠定器件基础[13].

当前,动态SLM 通常难以实现振幅和相位的同时调制.为了匹配动态SLM 的调制特性,物波函数的复振幅需要被编码为振幅型或相位型的计算全息图(computer-generated hologram,CGH)[14].纯相位型CGH 能量利用率高、共轭像易于消除,是动态三维信息的理想承载方式之一[15].不过,纯相位型CGH 舍弃了全息面上的振幅信息,降低了全息三维显示的图像质量.提升纯相位型CGH 显示质量的常用方法包括误差扩散法[16]、双相位编码法[17]、迭代编码法[18]及深度学习法[19]等.迭代编码法通过多次正、逆向的波前传播计算,可以优化全息面上的相位轮廓,进而提升纯相位型CGH的重建质量.Gerchberg-Saxton(GS)算法是一种典型的迭代优化算法[20],但常面临收敛速度受限的问题.加权GS 方法通过在像平面引入比例反馈因子的方式提升了迭代计算的收敛速度[21],但部分结果仍存在迭代发散、收敛速度偏慢以及重建质量受限等问题,需要进一步优化提升.

本文提出了一种基于角谱传播的自适应混合约束迭代(adaptive mixed constraint Gerchberg-Saxton,AMCGS)算法.该算法基于自适应的反馈机制和频带约束策略,在迭代过程中为像平面和全息平面的不同区域设置自适应的反馈因子,提升了迭代优化过程的收敛速度和稳定性,在较短的计算时间内获得了更高重建质量的纯相位型CGH,可以应用在高质量的全息显示场景中.

2 理论方法

2.1 角谱传播模型

纯相位型CGH 的迭代优化方法需要基于特定的波前传播模型进行设计,如傅里叶变换模型、菲涅耳衍射模型和角谱传播模型等.其中,傅里叶变换模型模拟夫琅禾费衍射,可用于远场衍射分布的计算,但对于三维场景的适用性较弱,需要进行针对性优化;菲涅耳衍射模型的物面采样间距与传输距离相关,增加了计算难度.角谱传播模型可以精确模拟平面波集的光学传播过程,物面采样间距与传输距离无关.因此,本文提出的AMCGS 算法基于角谱传播模型设计.平面波集由全息面传播到像平面的过程定义为正向角谱传播过程,其数学形式可描述为

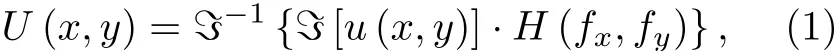
式中,ℑ表示傅里叶变换,ℑ−1表示逆傅里叶变换;u(x,y)表示全息面的复振幅分布,U(x,y) 表示像平面的复振幅分布;H(fx,fy) 表示与传播距离z相关的传递函数,其具体形式为

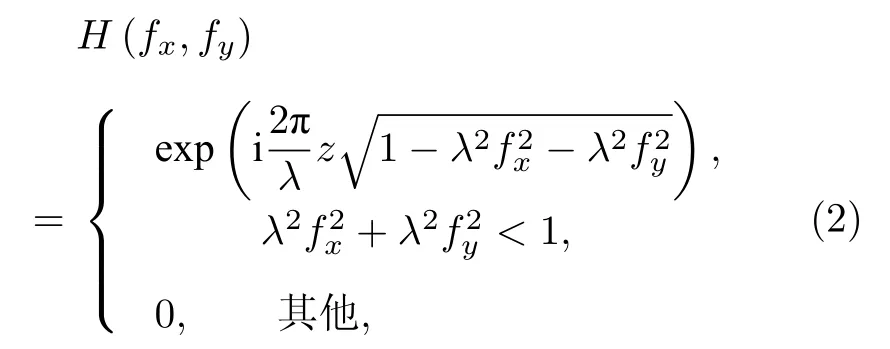
其中,λ表示照明波长,fx和fy分别表示沿x轴与y轴方向的空间频率.同理,平面波集由像平面传播到全息面的过程定义为逆向角谱传播过程.

为了获得全息面上的复振幅分布,提取复振幅U(x,y)的相位,并使用逆向角谱传播模型:

式中,arg 表示提取相位,A(x,y) 表示像平面上受到约束的振幅,H−z(fx,fy) 表示与传播距离z相关的逆向传递函数,u′(x,y) 表示经逆向传播获取的全息面复振幅.通过多次受约束的正、逆向角谱传播,全息面上的相位轮廓可以得到优化,进而得到重建质量更高的纯相位型CGH.

2.2 AMCGS 算法模型

传统GS 算法的迭代约束对所有采样点赋予相同的权值.这一反馈策略限制迭代优化的自由度,降低了迭代过程的收敛速度和稳定性.在像平面上设置信号区和噪声区,并为不同区域设置不同的反馈权值,可以增加迭代优化的自由度[22],进而加快迭代优化的收敛速度[23].AMCGS 算法对于信号区与噪声区的设置如图1 所示.在迭代过程中,目标图像需要扩展到原先尺寸的2 倍.由原图像构成的中心区域为信号区,由采样点扩展获得的边缘区域为噪声区.

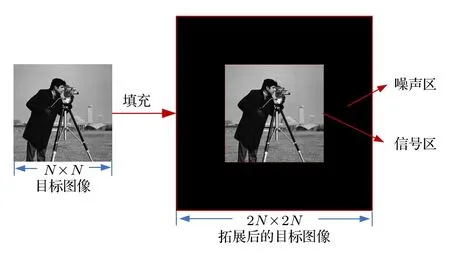
图1 AMCGS 算法中的信号区与噪声区Fig.1.Signal area and noise area on the reconstruction plane in the AMCGS algorithm.

对于原始采样点数为N×N的目标图像,AMCGS算法的流程如图2 所示.为了按照图1 所示方法在像平面构建出信号区和噪声区,像平面的图像采样点数首先设置为2N×2N[24].考虑到角谱传播模型的全息面和像平面采样点数相同,因此在第一次迭代中,采样点数为2N×2N的均匀振幅和随机相位构成了全息面的初始复振幅分布.使用正向角谱传播模型即(1)式,可获得初始复振幅分布在像平面上对应的重建复振幅分布.在执行逆向角谱传播前,按照如下策略对像平面的重建振幅进行约束:

图2 AMCGS 算法原理图Fig.2.Schematic of AMCGS algorithm.

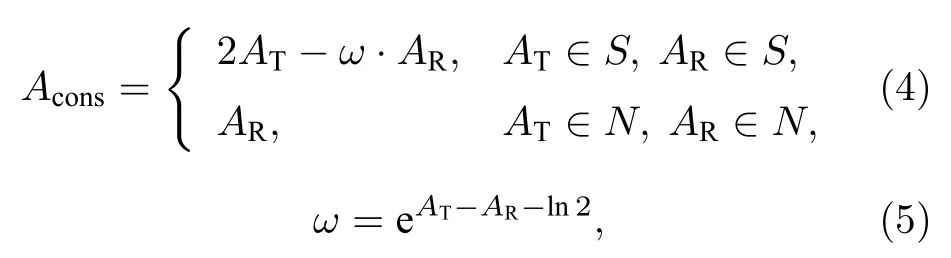
式中,S为信号区,N为噪声区,AT为目标图像的振幅分布,AR为像平面的重建振幅分布,Acons为经过自适应混合约束后的振幅,ω为自适应振幅约束系数.ω会随着迭代过程变化,自适应地优化迭代步长以调整迭代进程.

提取复振幅(1)式的相位,与约束振幅(4)式共同构成像平面的约束复振幅.使用逆向角谱传播模型(3)式,可获得约束复振幅分布在全息面上的复振幅分布.提取全息面复振幅(3)式的相位,即可获得采样点数为2N×2N的纯相位型CGH.由图2 可以看出,噪声区的引入增加了纯相位型CGH的采样点数.对于原始采样点数为N×N的目标图像,未经处理的CGH 采样点数为2N×2N.然而,在全息再现过程中,上述纯相位型CGH 边缘像素对应的重建区域主要为噪声区.这些边缘像素不仅对目标物体全息再现的贡献较小,还限制了系统的空间带宽积利用率和光能利用率.为了避免空间带宽积的浪费,第二次迭代前需要对纯相位型CGH边缘像素进行优化.AMCGS 算法首先基于频带约束策略对采样点数为2N×2N的CGH 进行了裁切,仅保留了其中心区域的N×N个像素;其次将采样点数为N×N的CGH 再次拓展为2N×2N,以保证其在像平面的重建结果仍旧可以构建出信号区和噪声区.为了避免光能的浪费,在上述采样点拓展过程中,纯相位型CGH 的边缘像素取值均为0.第二次及以后的迭代过程均使用采样点数为2N×2N的均匀振幅和补零拓展后的纯相位型CGH 构成全息面的复振幅.重复自适应迭代过程(1)式—(5)式,直至达到预设的循环次数,即可获得目标图像经过优化的纯相位型CGH.

2.3 有效传播距离

除了可以提升迭代优化的自由度,AMCGS 算法还可以拓展角谱传播模型的有效距离.简便起见,以一维角谱传播模型为例,讨论角谱传播模型的有效距离.此时,角谱传递函数即(2)式可简化为

提取一维角谱传递函数的相位,可以得到

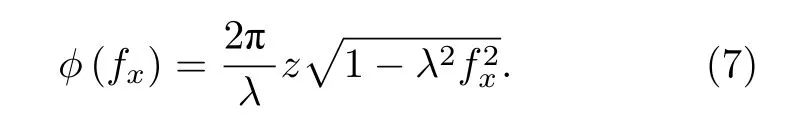
相位函数ϕ(fx) 的局域空间频率为

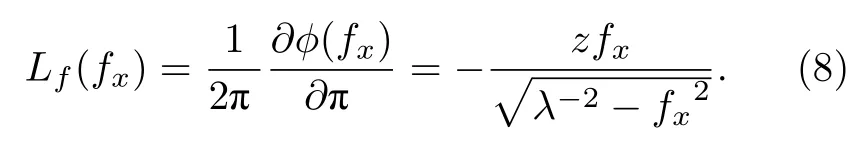
为了避免角谱传播模型中的混叠误差,一维采样过程中,频率采样间隔需要满足奈奎斯特采样定理:

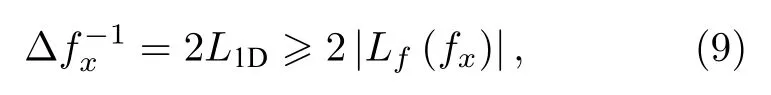
式中,Δfx为频率采样间隔,L1D为一维全息平面的总宽度.考虑到(8)式的单调性,为了使(9)式始终成立,仅需保证(9)式在fx取最大值时成立即可.此时,重建距离z需要满足:

式中,N1D为一维采样点数,Δx1D为一维采样间隔,zmax为一维角谱传播模型的有效传播距离.AMCGS 算法在构建信号区和噪声区的过程中将目标图像采样点数扩展到原始尺寸的2 倍,因此其有效距离也将扩展为传统角谱传播模型的2 倍.

3 数值仿真与分析

本文用峰值信噪比(peak signal-to-noise ratio,PSNR)和相关系数(correlation coefficient,CC)评价全息再现的图像质量.其中,PSNR (单位:dB)的数学形式为

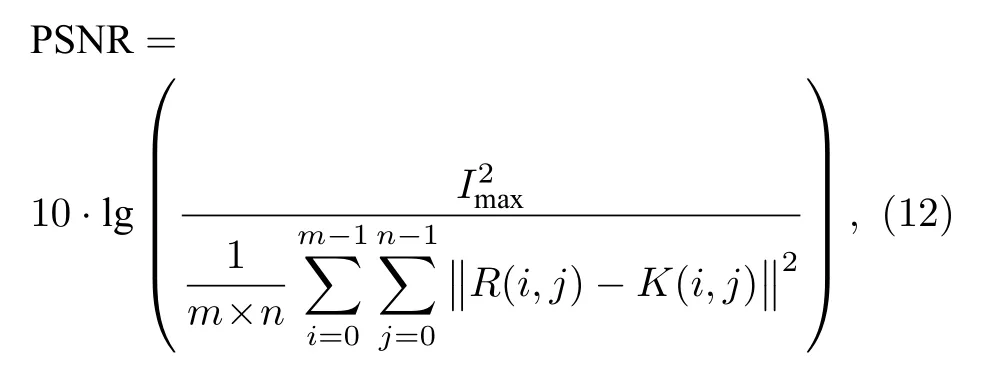
式中,Imax表示图像的最大灰阶值,R和K分别表示目标图像与重建图像的振幅分布.PSNR 取值越高,重建图像的质量相对越好.CC 的数学形式为

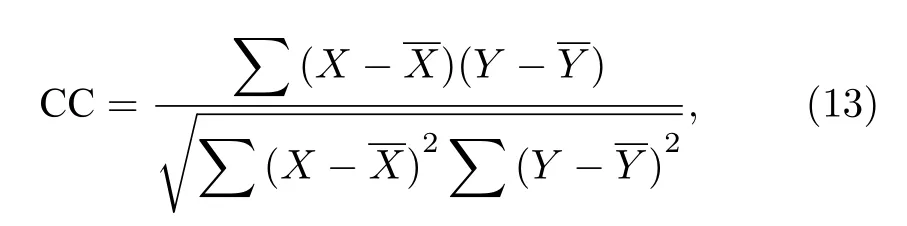
式中,X和X分别表示目标图像的振幅分布和振幅均值,Y和Y分别表示重建图像的振幅分布和振幅均值.CC 取值越大,两幅图像的相关性越强.

本文采用图3(a)—(d)所示的狒狒(baboon),船(ship),芭芭拉(barbara),女人(women)四幅图像作为目标图像.上述目标图像的原始采样点数均为512×512,补零填充后采样点数扩展至1024×1024.图3(e)—(h)展示了没有加入频带约束策略时,不同迭代次数下全息再现结果的PSNR 值.当迭代次数小于20 时,目标图像全息再现结果的PSNR 值随着迭代次数的增加快速提升;当迭代次数大于40 时,目标图像全息再现结果的PSNR 值渐渐趋于稳定.仿真结果表明,本文设计的反馈策略具有稳定的收敛性,且全息再现质量相比非迭代算法提升显著.

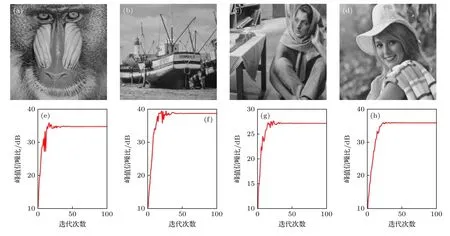
图3 目标图像(a)—(d)及其AMCGS 反馈策略仿真重建结果(e)—(h) (a),(e) 狒狒;(b),(f) 船;(c),(g) 芭芭拉;(d),(h) 女人Fig.3.Target images (a)–(d) and corresponding simulation results by the proposed AMCGS feedback (e)–(h): (a),(e) Baboon;(b),(f) ship;(c),(g) barbara;(d),(h) women.

为了提升空间带宽积和光能的利用率,将频带约束引入上述反馈策略,得到完整的AMCGS算法.同时,将加入频带约束的传统GS 算法命名为RSGS 算法,作为对照组进行仿真实验.针对图3(a)—(d)的4 个目标图像,AMCGS 算法和RSGS算法重建结果的CC 值随迭代次数变化的曲线,在图4(a)—(d)中给出.可以看出,随着迭代次数的增加,AMCGS 算法再现结果的CC 值比RSGS 算法更大,其再现图像与原始图像的相关性更高.在迭代100 次时,AMCGS 算法全息再现结果的CC值平均约为0.9857;在迭代300 次时,AMCGS 算法全息再现结果的CC 值平均约为0.9934,此时AMCGS 算法已趋近于收敛.AMCGS 算法100 次迭代得到的全息再现图像已经可以满足人眼视觉质量要求.PSNR 作为评价全息再现质量的又一定量指标,本文基于计算成本与全息再现质量间的平衡,绘制了AMCGS 算法和RSGS 算法迭代100 次PSNR 值的变化曲线,如图5(a)—(d)所示.在迭代100 次时,AMCGS 算法全息再现结果的PSNR平均值约为31 dB,相比RSGS 算法平均提升了约5 dB,得到的全息再现结果已可以应用于高质量全息显示.上述结果均证实本文提出的AMCGS算法能获得更好的全息再现质量.大量增加迭代次数以测试AMCGS 算法再现结果的PSNR 值随迭代次数变化的关系,迭代2×104次时再现图像的PSNR 值为41.47 dB,迭代105次时再现图像的PSNR 值为42.7 dB,仅提升1.2 dB 左右.2×104次迭代后PSNR 值随迭代次数变化曲线趋于收敛,大幅度增加迭代次数对再现图像PSNR 值的提升较为有限.

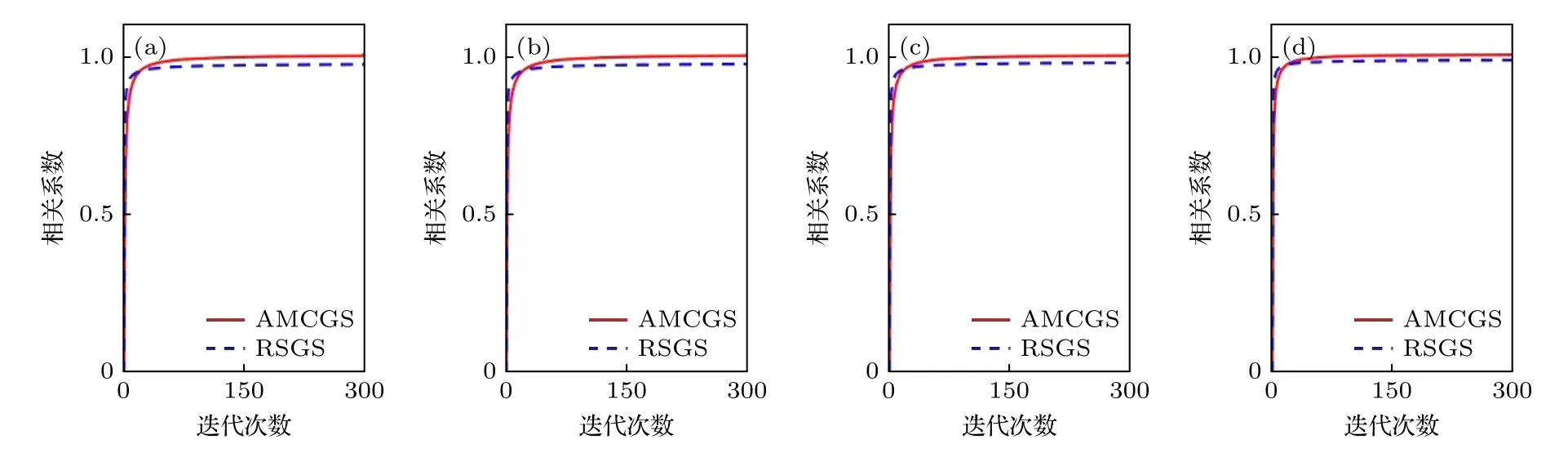
图4 AMCGS 算法与RSGS 算法仿真重建结果CC 值随迭代次数的变化曲线 (a) 狒狒;(b) 船;(c) 芭芭拉;(d) 女人Fig.4.CCs under different iteration numbers of the reconstructions by the AMCGS algorithm and RSGS algorithm: (a) Baboon;(b) ship;(c) barbara;(d) women.

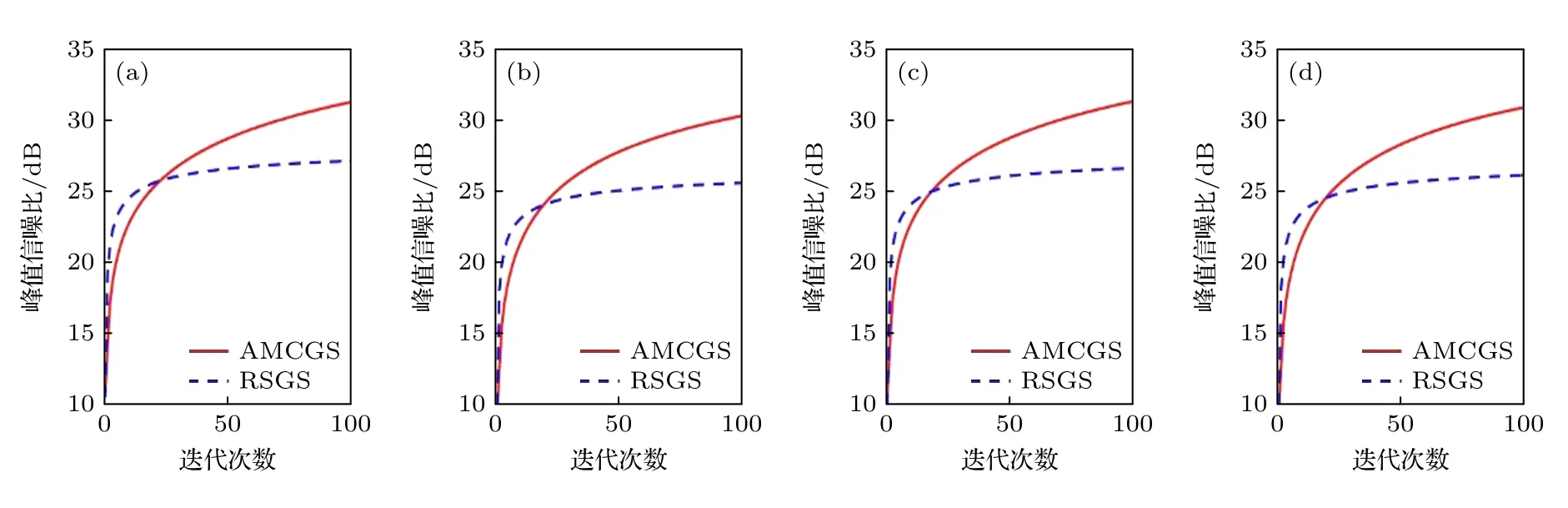
图5 AMCGS 算法与RSGS 算法仿真重建结果PSNR 值随迭代次数的变化曲线 (a) 狒狒;(b) 船;(c) 芭芭拉;(d) 女人Fig.5.PSNRs under different iteration numbers of the reconstructions by the AMCGS algorithm and RSGS algorithm: (a) Baboon;(b) ship;(c) barbara;(d) women.

将传统随机相位法和AMCGS 算法分别应用于4 个目标图像,传统随机相位法对应的全息再现结果,如图6(a)—(d)所示,迭代100 次,AMCGS算法对应的全息再现结果如图6(e)—(h)所示.对于不同的目标图像,AMCGS 算法均可以取得良好的全息再现质量,相应的全息再现图像对比度高,图像的细节清晰可见,更符合人眼视觉质量要求.使用CC 作为评价指标,AMCGS 算法的全息再现结果较传统随机相位法平均提升了约0.45;使用PSNR 作为评价指标,AMCGS 算法的全息再现结果较传统随机相位法平均提升了约20 dB.

图6 全息再现仿真结果对比 (a)—(d) 传统随机相位法;(e)—(h) AMCGS 算法Fig.6.Comparison of holographic reconstructions simulation results: (a)–(d) Traditional random-phase method;(e)–(h) AMCGS algorithm.

本文仿真实验所采用的计算平台为Matlab-2021b,Windows 10 操作系统和Core I5-11400H(2.70 GHz).100 次迭代后,AMCGS 算法可以达到符合人眼视觉质量的全息再现结果.基于计算成本与全息再现质量间的平衡,针对4 个目标图像,采样点数设置为512×512.传统GS 算法,RSGS算法以及AMCGS 算法完成迭代所需时间见表1.从表1 可以看出,AMCGS 算法相较于无需增加采样数的传统GS 算法,其迭代时间较长,然而传统GS 算法难以用于高质量全息显示场景;AMCGS算法相较于同样增加采样数的RSGS 算法,二者迭代时间相差无几,结合图5 可知,100 次迭代后AMCGS 算法全息再现结果的PSNR 值相比于RSGS 算法平均提升了约5 dB,且AMCGS 算法具有更大的优化空间.

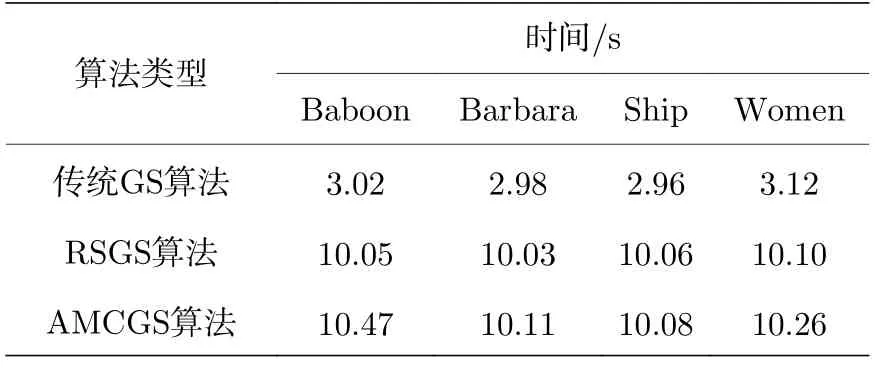
表1 传统GS 算法,RSGS 算法 以及AMCGS算法迭代100 次所需时间Table 1.Time required for 100 iterations of GS algorithm,RSGS algorithm and AMCGS algorithm.

4 光学实验

为了进一步探索AMCGS 算法在光学实验中的重建质量,本文构建了如图7 所示的光学系统.波长为532 nm 的相干光束通过衰减片、空间滤波器、准直透镜和起偏器后成为对SLM 调制敏感的平面照明波.纯相位型CGH 加载在SLM 上,用以调制平面照明波.实验中使用的SLM 型号为HoloEye Gaea-2Vis,其像素间距为3.74 µm,采样点数为3840×2160.经过纯相位型CGH 调制的重建光波经过4f系统滤波后,由Cannon 500D 相机采集.

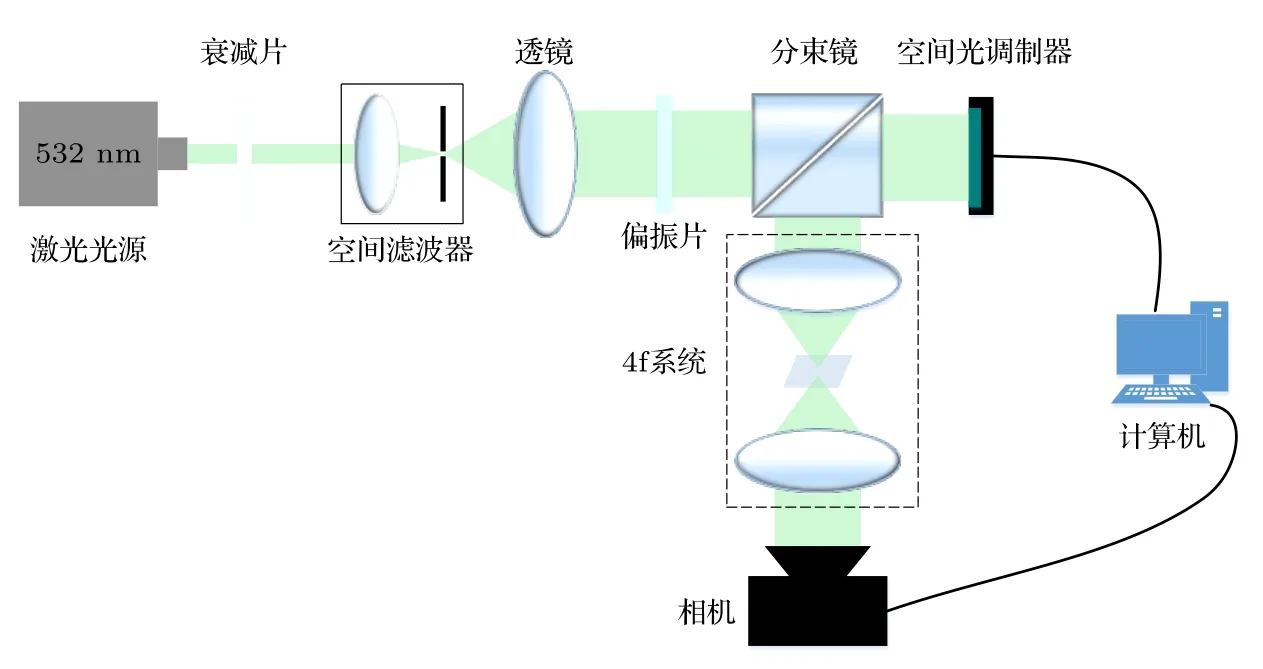
图7 光学实验系统结构Fig.7.Schematic of optical experimental setup.

光学重建结果如图8 所示.对于不同的目标物体,AMCGS 算法的光学重建结果的对比度较好、散斑噪声较弱且亮度分布均匀,与数值仿真中取得的结果相似.实验重建结果证明了AMCGS 算法的实际有效性.

图8 光学实验结果对比 (a)—(d) 传统随机相位法;(e)—(h) AMCGS 算法Fig.8.Comparison of optics experimental results: (a)–(d) Conventional random phase method;(e)–(h) AMCGS algorithm.

5 结论

本文提出了一种基于角谱传播模型的AMCGS算法.该算法将像平面分割为信号区和噪声区,通过在不同区域加入不同的自适应反馈机制,提升了迭代优化的稳定性和收敛速度;在全息面使用频带约束策略,提升了空间带宽积和光能的利用率,提高了全息再现的图像质量.实验表明,针对不同的目标物体,AMCGS 算法全息再现结果的PSNR值相比RSGS 算法平均提升了约5 dB,CC 值相比RSGS 算法平均提升了约0.025,且重建图像具有更高的对比度、更低的散斑噪声和更均匀的亮度分布.AMCGS 算法对于高质量的全息显示具有重要的应用价值.