半导体激光阵列谱合束系统中光束串扰物理机制分析*

庄英豪 傅芸 蔡伟 张青松 吴真† 郭林辉 钟哲强 张彬

1) (西华大学理学院,成都 610039)

2) (中国工程物理研究院应用电子学研究所,绵阳 621900)

3) (四川大学电子信息学院,成都 610064)

在外腔反馈半导体激光谱合束系统中,由于半导体激光阵列的“smile”效应、外腔中光学元件制作误差等因素,激光阵列一子单元发射光束经过外腔返回注入其他子单元,在两子单元之间形成光束串扰并影响合束特性.本文从耦合腔光束谐振角度出发,基于光反馈半导体激光器速率方程,构建了耦合腔谐振模型,推导了激光器稳态输出时能在耦合腔中起振的光束模式.结合耦合腔模式竞争机制与耦合腔谐振模型分析由两子单元间距变化引起的不同串扰对锁定光谱和合束效率的影响.结果表明子单元间的串扰行为会造成光谱峰值下降、光谱偏移、边缘毛刺以及合束效率劣化.相比距离更远的两子单元之间的高阶串扰,距离更近的两子单元间的低阶串扰对合束特性的劣化程度更大.最后,为证明该模型的正确性和有效性,对所得分析结果进行了实验验证,实验观测到在串扰影响下的光谱结构与理论分析一致.

1 引言

半导体激光器因其体积小、效率高、使用寿命长等优势被应用于许多领域,如医疗仪器、军事、激光测距、激光打印等[1−3].随着半导体激光技术在各个领域不断发展,人们对激光器输出功率、光束质量提出了更高的要求.因此,兼具高功率高光束质量的半导体激光光源被广泛研究[4].由于半导体激光器的特殊结构和工作原理,其光束质量总是随着功率提高而恶化,外腔光谱合束(spectral beam combining,SBC)技术可以有效解决该问题,其最早由美国麻省理工学院林肯实验室提出[5].目前,研究人员对SBC 系统进行了系列研究.2010 年,丹麦技术大学的Vijayakumar 等[6]实现了980 nm半导体激光器光谱合束,获得了9.3 W 连续输出功率,M2因子为5.3,合束效率为63%.为提升半导体激光光谱合束效率,2012 年美国Teradiode公司[7,8]基于光谱合束技术实现360 W、2 倍衍射极限、亮度达10 GW/(cm2·sr)的半导体激光源,将传统的千瓦级半导体激光器亮度提高了100 倍.由于半导体激光阵列的“smile”效应、发散角,以及光学元件误差等因素,实际谱合束系统中光束串扰总是不可避免,其成为劣化谱合束光束特性的主要因素之一[9].2021 年,Ma 等[10]利用外腔光束传输理论构建了含串扰的谱合束系统分析模型,较好地估计了光束大小和远场发散角,并提出在光栅外腔中引入空间滤波器抑制串扰来提高光束质量.2022 年,Song 等[11]研究发现,通过增加倒置开普勒望远镜、减小透射透镜的焦距或增大光栅与输出耦合镜的间距,可以抑制串扰.光束串扰作为谱合束系统中极易出现的物理现象[12],其严重影响合成光束的光谱结构、光束质量、合束效率和输出光斑.目前国内研究人员针对抑制子单元串扰进而提升合束特性的文献较多[11,13,14],为促进谱合束光源的应用做出了杰出贡献.

本文基于实验观测的半导体激光子单元有串扰存在时的光谱结构,采用Lang-Kobayashi 光反馈半导体激光器速率方程,构建了谱合束系统的耦合腔光束谐振模型,结合耦合腔模式竞争的物理机制分析不同子单元间串扰对光谱结构的影响,建立的物理模型与实验现象契合较好.在此基础上分析了串扰对光斑分布和合束效率的影响,并提出通过添加伽利略望远镜系统抑制串扰.

2 谱合束系统原理

SBC 系统主要由半导体激光阵列、快轴准直镜、慢轴准直镜、变换透镜、介质膜光栅、输出耦合镜构成.如图1 所示,光束由快慢轴准直镜准直后经过变换透镜以不同的入射角重叠至光栅,由光栅色散后以同一角度入射至输出耦合镜,部分光束被输出耦合镜反射回激光阵列形成光反馈帮助子单元锁定光谱.SBC 系统可视为由3 个反射镜组成的耦合腔结构,半导体激光子单元的后端面和前端面构成内腔,后端面和输出耦合镜构成外腔.理想情况下,各子单元发射光束经由外腔反馈后注入自身子单元协助该子单元锁定光谱,锁定光谱的光束由光栅逆色散沿相同角度衍射至耦合镜.但是,实际谱合束系统中,反馈光束可能注入其他子单元进而影响光谱锁定.如图1 所示,中心子单元发射光束由外腔反馈到1 号子单元,即部分光束将在中心子单元后端面→耦合镜→1 号子单元后端面→耦合镜→中心子单元后端面之间构成的新耦合腔中振荡,形成光束串扰,本文中称为一阶串扰.类似地,中心子单元发射光束注入到2 号(3 号)子单元,在中心子单元后端面和2 号(3 号)子单元后端面之间谐振,本文称为二阶(三阶)串扰.图1 中蓝色虚线表示中心子单元发射光由外腔反馈到1 号子单元形成一阶串扰光路径,绿色虚线、紫色虚线分别为二阶、三阶串扰光路径.

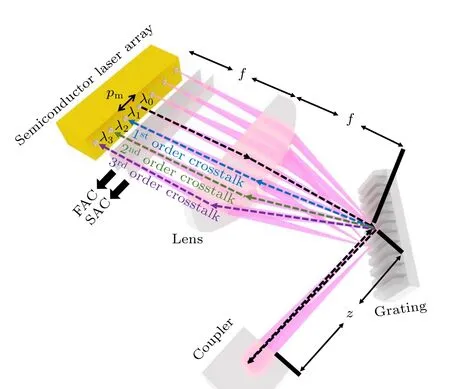
图1 外腔反馈光谱合束原理图Fig.1.SBC with external cavity feedback.

2.1 串扰光束中心波长计算模型

中心子单元光束以角度β0入射,根据光栅方程d(sinβ– sinγ)=λ,第m号子单元入射角与β0的几何关系βm=β0– arctan(mΔp/f),第m个子单元波长为

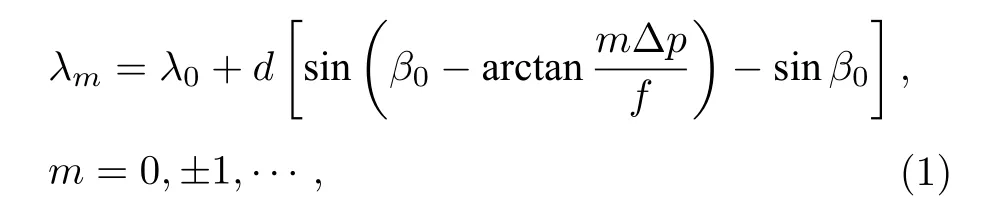
其中λ0为中心子单元光束的波长,d为光栅周期,γ为衍射角,Δp为相邻子单元间距,f为变换透镜焦距,z为光栅与输出耦合镜之间的距离.

中心子单元波长λ0,1 号子单元波长λ1,一阶串扰光波长λ01表示为[12]

将(2)式推广到第m个子单元与第n个子单元之间串扰光波长:

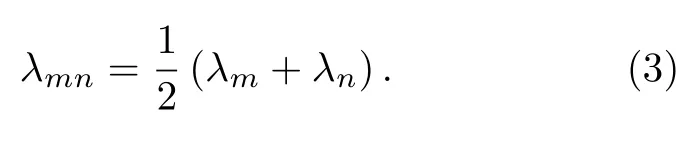
2.2 半导体激光阵列谐振频率计算模型

利用Lang-Kobayashi 光反馈半导体激光器速率方程描述串扰行为[15]:

式中R=J/eV为单位体积的载流子注入速率,J为注入电流密度,e为电子电荷,V为有源区体积,τc为载流子寿命.(6)式等号右边第1 项表示注入电流产生的载流子密度增加,第2 项表示载流子寿命引起的载流子密度减少,第3 项表示增益引起的载流子密度减小.当激光器处于稳定工作状态,即dE0(t)/dt=0,dN(t)/dt=0,得到耦合腔谐振相位条件[12]:

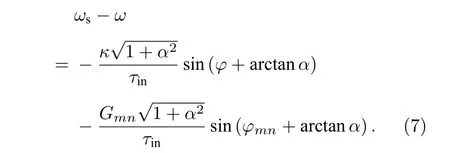
等号右边第1 项由自激振荡引起,第2 项由串扰引起,w由外腔注入光的谐振频率决定:

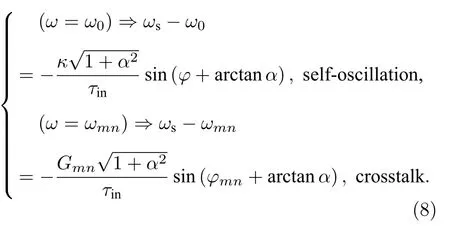
以中心子单元为例,当耦合腔由中心子单元自身后端面和输出耦合镜组成时,自激振荡的谐振频率由该耦合腔决定,谐振频率为w0,(8)式表明只有自激振荡时w=w0=2π/λ0;当耦合腔由m号子单元后端面、输出耦合镜和n号子单元后端面组成时,串扰光束的谐振频率由该耦合腔确定,谐振频率为wmn,即w=wmn=2π/λmn,λmn由(3)式确定.

2.3 实验方案

为研究串扰对输出光谱特性的影响,采用中心波长为980 nm 的两个单管半导体激光器进行实验.每个激光器在注入电流为16 A 时,输出功率为14.09 W,电光效率为39.4%,使用Yokogawa 6370D 光谱仪观察两个激光子单元分别在单独开启和共同开启时的光谱结构.通过改变两个单管半导体激光器的间距产生如图1 谱合束系统中所示的1 号、2 号、3 号子单元与中心子单元之间的一阶、二阶、三阶串扰.如图2 所示,激光子单元集成在LD 芯片上,除此之外每个子单元后还集成了快轴准直镜、慢轴准直镜以及倾斜45°反射率达99%的高反镜.快轴准直镜焦距fF为900 mm,用于准直快轴光束,慢轴准直镜焦距fS为13 mm,用于准直慢轴光束,两只单管半导体激光器在快轴上进行光谱组合.变换透镜焦距f为33 cm,其将两个激光子单元以Littrow 角度入射至光栅.选择反射率为10%的输出耦合镜,固定在距离光栅300 mm处,将光栅衍射的光束耦合输出.输出光束经过分束镜分束,一部分由光谱仪扫描记录光谱结构,另一部分由功率计检测输出功率.

图2 谱合束实验装置图Fig.2.Experimental installing of SBC.

3 理论分析和实验对比

采用中心波长为980 nm 的两个单管半导体激光器进行仿真计算,其他主要模拟参数取[16,17]n=3.5,τc=2 ns,N0=2.5×1018cm–1,V=1.6 × 10–16cm3,J=3.125 × 1014A/m2,GN=2.25 × 10–12m3/s,z=30 cm,α=6,Γ=1,Lin=400 µm,f=33 cm,d–1=1600 line/mm.根据(1),(3),(8)式,当Δp取300 µm 时,模拟激光子单元之间产生的一阶串扰对光谱特性的影响.类似地,当Δp取600 µm 和900 µm 时,模拟激光子单元之间产生的二阶和三阶串扰对光谱特性的影响.

3.1 一阶串扰

图3 将子单元间隔Δp设置为300 µm 模拟分析一阶串扰.分析(8)式得到图3(a)相位曲线图[16],其中橙色实线为中心子单元自激振荡相位图,蓝色实线为1 号子单元自激振荡相位图,黑色实线为一阶串扰光相位图.曲线与横轴交点为(8)式的解,其对应耦合腔内可能稳定起振模式的波长.在图3(a)的基础之上,图3(b)中给出了一阶串扰对光谱结构的影响.其中橙色虚线和蓝色虚线分别为中心子单元和1 号子单元单独发光时的光谱结构(线条颜色与图3(a)对应).图中锁定范围Δλ0=Δλ1=0.5 nm 对应图3(b)中光谱的宽度,两子单元单独发光时光谱明显分离且边缘光滑.黑色实线为两子单元间存在一阶串扰时的光谱结构,光谱存在两个主峰,相比于单个子单元发光,光谱强度下降且边缘出现毛刺峰变得粗糙,毛刺峰对应的波长分别为981.37,981.52,981.65 nm.蓝色虚线所示主峰波长为981.25 nm,存在串扰时其波长偏离至981.3 nm.结合图3(a)分析其原因在于: 光谱锁定范围中交点对应的模式能否起振取决于该点的反转粒子数密度,如果某一点的反转粒子数密度较高,阈值增益较低,那么该点对应的模式就能够起振[18,19].此外,可能起振的模式之间会相互竞争,最终增益差最大(反转粒子数密度最高,阈值增益最低)的点对应的模式成为主模式,主模式锁定起振后,其他点对应的模式或被抑制,或能突破阈值增益起振成为光谱周围的毛刺峰.换言之,两子单元以及串扰光的主模式都由模式竞争机制随机锁定,所以子单元间的串扰可能导致光谱主峰发生一定偏移[20].其次,串扰光主模式和毛刺峰会消耗一部分反转粒子数起振,致使原光谱主峰强度下降.图3(a)中锁定范围Δλ01=0.23 nm 应对应图3(b)中串扰光光谱宽度,但图3(b)中并未出现明显侧峰.这是因为当两子单元间隔为300 µm 时一阶串扰光的相位曲线分别与两子单元自激振荡相位曲线重叠,对应一阶串扰光光谱与两子单元光谱重叠,因此整个光谱结构中并未观察到串扰形成的侧峰,只显示子单元光谱变宽且有重叠.

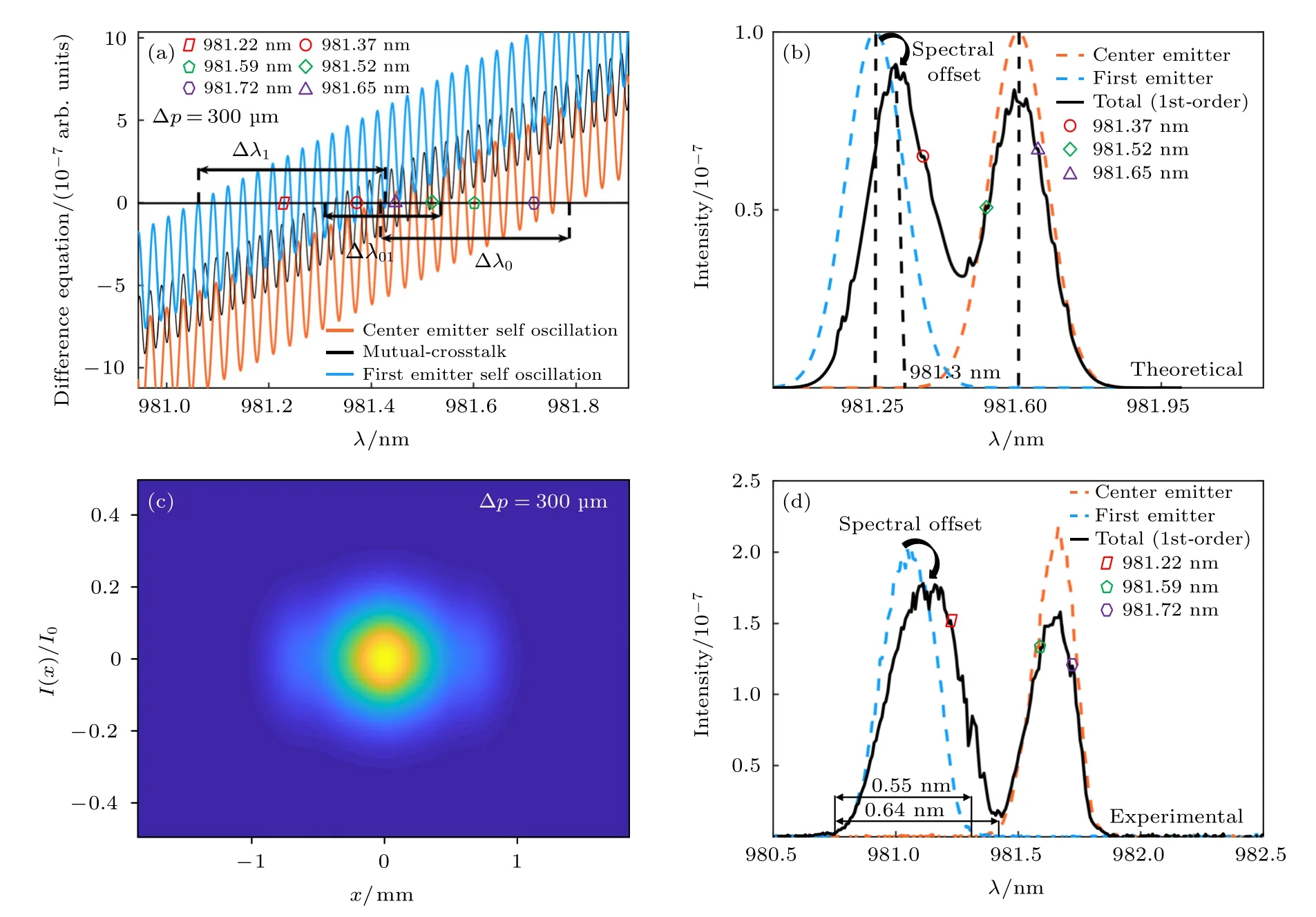
图3 一阶串扰对光束特性的影响 (a) 自激振荡与串扰相位图;(b) 锁定光谱;(c) 合束光斑;(d) 实验观测一阶串扰下的光谱结构Fig.3.Effect of 1st crosstalk on beam properties: (a) Self-oscillation and crosstalk phase diagram;(b) the spectral structure;(c) beam spot;(d) experimental measurement of spectra.

为了分析串扰对合束光斑的影响,采用衍射积分方法[16]模拟了输出耦合镜的光斑和合束效率,无串扰影响下的合束效率为80.1%.图3(c)为一阶串扰影响下的合束光斑,串扰导致明显的旁瓣,合束效率为45.5%,严重劣化.为进一步验证理论分析结果,图3(d)为实验观测结果.橙色虚线与蓝色虚线分别为单独开启中心子单元与1 号子单元观测到的光谱结构,光谱明显分离且边缘光滑,光谱宽度与图3(a)中光谱锁定宽度大致吻合.黑色实线为同时开启中心子单元与1 号子单元观测到的光谱结构,因模式竞争导致的光谱发生偏移,光谱边缘出现毛刺峰,其波长分别为981.22,981.59,981.72 nm.1 号子单元光谱变宽,由0.55 nm 增大到0.64 nm.光谱高度下降等观测结果都与理论模拟相契合.通过耦合腔谐振模型和模式竞争机制很好地解释了实验图中观察到的光谱结构.

3.2 二阶串扰

图4 为当子单元间隔Δp为600 µm 时二阶串扰对合束特性的影响.图4(a)中橙色实线和蓝色实线分别为中心子单元和2 号子单元自激振荡相位图,黑色实线为二阶串扰光的相位图.图4(b)中橙色虚线和蓝色虚线分别为单独开启中心子单元和2 号子单元时的光谱结构.图4(a)中Δλ0=Δλ2=0.5 nm 对应图4(b)橙色虚线和蓝色虚线的光谱宽度.黑色实线为两子单元存在二阶光束串扰时的光谱结构,光谱存在两个主峰,光谱边缘出现毛刺峰,对应的波长分别为980.85,981.28 和981.52 nm.与一阶串扰相比,图4(a)中心子单元和2 号子单元自激振荡相位曲线与二阶串扰相位曲线分离,在光谱结构上表现为二阶串扰光光谱与两子单元光谱分离形成一个侧峰.侧峰波长为981.17 nm,侧峰光谱宽度对应图4(a)中Δλ02=0.21 nm.通过计算发现,在系统其他参数不变的情况下,Δp为光谱结构中由于串扰引起的侧峰是否存在的一个重要因素,当Δp<330 µm 时串扰光不会形成侧峰,只能使光谱变宽;当Δp≥ 330 µm时串扰光可能会在原光谱之间出现明显侧峰.此外,由于模式竞争效应,Δλ02范围中二阶串扰光的主模式随机锁定,其主模式波长偏离(3)式计算的理论值,在图中由理论值981.25 nm 偏移至981.17 nm.

图4(c)为二阶串扰影响下的合束光斑图,旁瓣与中心光斑分离较远,在有限大小的耦合镜面上,耦合效率降低进而致使合束效率减小,合束效率为50.2%.相比一阶串扰,二阶串扰对效率的劣化程度略小.

图4(d)给出了实验观测的二阶串扰下的光谱结构.橙色虚线与蓝色虚线分别表示中心子单元与2 号子单元单独发光时的光谱结构,两个光谱明显分离且相对光滑,光谱宽度与图4(a)中光谱锁定宽度大致吻合.黑色实线为中心子单元与2 号子单元同时发光时观测的光谱结构,两光谱之间出现明显侧峰且边缘出现毛刺峰,波长分别为980.87,981.24 和981.57 nm.可见二阶串扰产生的侧峰与边缘毛刺峰消耗反转粒子数起振,不仅改变了光谱结构而且导致光谱高度下降.

图4 二阶串扰对合束特性的影响 (a) 自激振荡与串扰相位图;(b) 锁定光谱;(c) 合束光斑;(d) 实验观测二阶串扰下的光谱结构Fig.4.Effect of 2nd crosstalk on beam properties: (a) Self-oscillation and crosstalk phase diagram;(b) the spectral structure;(c) beam spot;(d) experimental measurement of spectra.

3.3 三阶串扰

子单元间隔Δp设置为900 µm,图5 进一步分析了三阶串扰对光谱结构的影响.图5(a)中橙色实线为中心子单元自激振荡相位图,蓝色实线为3 号子单元自激振荡相位图,黑色实线为三阶串扰光相位图.图5(b)给出了三阶串扰对锁定光谱的影响.橙色虚线和蓝色虚线分别为中心子单元和3 号子单元的光谱结构,光谱依旧明显分离且光滑.图5(a)中锁定范围Δλ0=Δλ3=0.5 nm 对应橙色虚线和蓝色虚线的光谱宽度.黑色实线为子单元间存在三阶光束串扰时的光谱结构,串扰光光谱锁定范围Δλ03=0.16 nm.Δp为900 µm,满足大于 330 µm 的条件,能在两子单元光谱中间形成一个侧峰,模式波长为981.1 nm.该模式包含于Δλ03中能够消耗反转粒子数起振,因此其与(3)式计算的理论模式波长接近.

图5(c)为有三阶串扰存在时的合束光斑图,三阶串扰引起的旁瓣强度较一阶二阶串扰光明显降低,合束效率也会相对提高,合束效率为62.8%.图5(d)展示了实验观测三阶串扰影响下的光谱结构,图中橙色虚线与蓝色虚线分别为单独测量中心子单元与3 号子单元的光谱结构,黑色实线为中心子单元与3 号子单元同时发光测得的光谱结构,观测到三阶串扰光并没有在两子单元光谱之间形成侧峰.实验观测到三阶串扰光谱并不稳定,断开电源后再次接通可能会得到不同的结果.其原因在于当Δp=900 µm 时,子单元间距过大,导致反馈回到子单元的光激励太低无法起振形成侧峰,或者无法有效反馈到子单元.光谱侧峰不仅取决于Δp,而且还要满足有效反馈和阈值条件.此外,由于三阶串扰不稳定性,相比较于一阶、二阶串扰其对光谱结构的影响明显更小.

图5 三阶串扰对合束特性的影响 (a) 自激振荡与串扰相位图;(b) 锁定光谱;(c) 合束光斑;(d) 实验观测三阶串扰下的光谱结构Fig.5.Effect of 3 rd crosstalk on beam properties: (a) Self-oscillation and crosstalk phase diagram;(b) the spectral structure;(c) beam spot;(d) experimental measurement of spectra.

3.4 伽利略望远镜系统抑制串扰

串扰对谱合束光束特性存在显著影响[11,21,22],上述分析表明低阶串扰对于子单元的输出光谱的影响更加显著.随着串扰阶数上升(子单元间距增大),串扰对合束的影响降低.可见,通过增大子单元间距能在一定程度上抑制串扰.以二阶串扰光为例,图6 给出了添加放大倍数n=1.5 的伽利略望远镜系统抑制串扰对光谱的影响.与图4(b)对比发现光谱侧峰在一定程度上被抑制.图6(b)中二阶串扰引起的旁瓣强度明显降低,合束效率提高,合束效率为68.3%.此外,与开普勒望远镜系统对比,伽利略望远镜无实焦点,可防止激光强度过高而损坏设备[23].

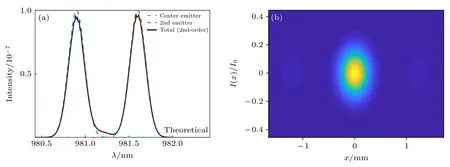
图6 (a) 抑制二阶串扰后的光谱;(b) 抑制二阶串扰后的合束光斑Fig.6.Spectra (a) and beam spot (b) after suppressing the second-order crosstalk.

4 结论

在光谱合束系统中,半导体激光阵列子单元之间的串扰易引起光束质量劣化,合束效率降低,进而限制其合束激光的应用.本文利用速率方程建立耦合腔谐振模型,探讨了光束串扰影响光谱的物理机制,依据谐振腔模型模拟了一阶、二阶、三阶串扰对光谱结构、输出光斑以及合束效率的影响.无串扰时合束效率为80.1%,但在一阶、二阶和三阶串扰下效率分别劣化为45.5%,50.2%和62.8%.一阶、二阶串扰对光谱的影响十分显著,二阶串扰形成明显的侧峰.一阶串扰虽无明显侧峰是由于子单元间距小于330 nm,串扰光光谱与原光谱重合,通过光谱变宽能显示串扰的影响;三阶串扰因其不稳定,较一阶、二阶串扰对光谱的影响较小.此外,内腔中模式竞争机制导致自激振荡、串扰锁定的波长与理论值有差异.合束系统中由于串扰的存在会使光束质量劣化,合束效率降低.模拟与实验结果表明增加子单元之间的间距能在一定程度上抑制串扰.进而提出通过在光栅外腔中添加n=1.5 的伽利略望远镜系统抑制串扰,模拟结果显示二阶串扰的侧峰被抑制,光斑图旁瓣强度减弱,系统的合束效率由50.2%提升至68.3%.该方法可以有效抑制子单元之间的串扰,在一定程度上提升合束效率.本文对半导体激光阵列谱合束系统子单元之间的串扰行为以及其影响光谱结构的物理机理进行了分析,为抑制子单元之间的串扰以及优化合束光谱结构提供理论依据.