基于ABAQUS的链条压出力理论分析与优化
2023-02-18李存志谢爱军刘毅
李存志,谢爱军,刘毅
(青岛征和工业股份有限公司,山东青岛 266700)
0 引言
标准滚子链及套筒链均由内链节、外链节相互串联组成,链节的连接牢固度是保证链条持续正常服役的前提。目前,针对链节牢固度的试验方法主要包括松动转矩和压出力。其中,压出力的测试方法是链条行业普遍认同的做法[1-2]。链节压出力理论计算方法是以机械设计中的弹性力学为依据,链传动设计手册做出了详细的阐述,为过盈量设计提供了一定的理论依据。但实际生产研发中,仍然存在不足之处。例如,现有的链节理论压出力计算方法并未考虑零件过盈接触表面边缘应力集中效应的影响,计算结果与实际试验验证结果存在较大差距。本文在详细分析过盈联接理论的基础上,结合有限元分析方法,针对链条链节压出力理论计算方法进行了改进优化,并且运用实际试验和ABAQUS有限元方法进行了验证,很大程度上降低了理论计算的误差,使得理论设计结果更加符合实际情况。
1 链条压出力理论计算
1.1 链条过盈压出力计算原理
链条的链节由外链板与销轴、内链板与套筒过盈配合而成,过盈配合使得零件接触表面之间产生径向结合压力Pi,链节接触表面基本尺寸如图1所示,在结合压力的作用下产生的阻碍轴向移动的摩擦阻力即为链条过盈压出力Fxe。
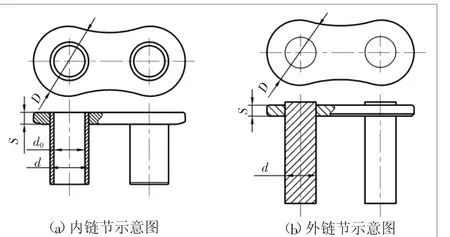
图1 链节接触表面基本尺寸示意图
由弹性力学和链传动技术手册可得,链条过盈所传递的力F为

式中:d为配合直径;s为链板厚度;f为摩擦因数;h1、h2为包容件与被包容件的表面粗糙度;E1、E2为材料的弹性模量;δmin为设计最小过盈量。其中刚度系数c1、c2分别取[3-4]:

式中:u1、u2为材料的泊松比;D为包容件外径;d0为被包容件外径。
由于链节采用压装的方式进行装配,所需的压出力Fxe为[5]

实际理论计算时,由设计最小过盈量δmin可得出接触表面的结合压力Pi,然后可求出过盈配合零件之间的压出力值Fxe。
1.2 链条压出力理论的应用
下面以某规格链条为例进行压出力的计算分析,链条各零部件材料、关键尺寸等所需模型参数数据如表1所示。
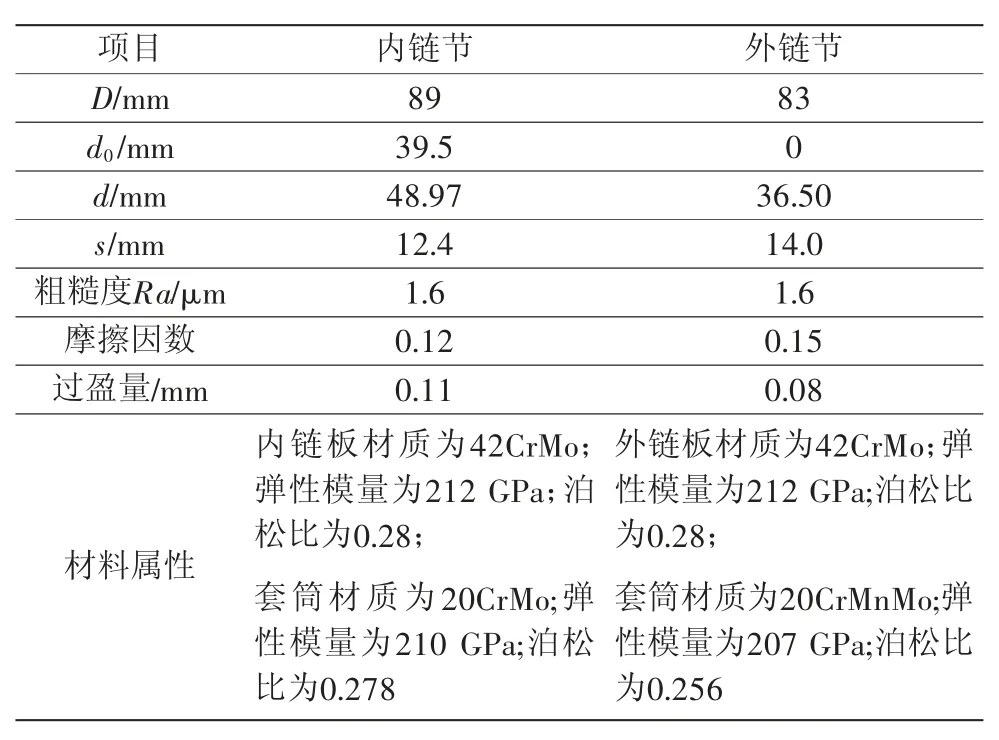
表1 模型参数数据表
由式(1)~式(6)可得,内单节理论接触压力为69.58 MPa,过盈所传递的力F为15.97 kN,则所需理论压出力均值Fxe=22.36 kN,外单节理论接触压力为175.43 MPa,过盈所传递的力F为42.25 kN,则所需理论压出力均值Fxe=52.40 kN。
在过盈配合表面的接触压力沿轴向均匀分布假设前提下,通过上述原理可以得到理论接触压力和压出力结果,但是由于弹性力学的局限性,无法求解过盈配合边缘应力集中所产生的接触压力变化[6],这样使得理论设计计算与实际情况不相符合,按照所需的压出力理论求解得到的过盈量偏大很多,造成整个链条的疲劳寿命大幅度降低[7-8]。
2 有限元模型的建立与分析
一方面为了掌握链节过盈配合时表面接触压力的分布规律、边缘应力集中的影响与压出力之间的关系,另一方面进行理论计算和有限元分析结果的对比。在ABAQUS中进行内链节有限元模型的建立,模型及边界如图2所示,整个模型包含154 836个C3D8R六面体网格。材料均采用理想的弹塑性本构模型,其属性如表1所示。在内链板内孔与套筒外径过盈连接的相互作用下,通过套筒轴向位移产生的支反力RF来体现内链节压出力的大小。

图2 内链节模型及边界
通过ABAQUS有限元分析,在内链板内孔和套筒外径之间过盈量0.11 mm下,两者表面之间的接触压力局部分布云图如图3所示。接触压力沿轴向并不是均匀分布的,套筒内侧边缘区域有明显的边缘应力集中现象,接触压力沿轴向逐渐递减。沿过盈配合区域轴向进行节点路径上的接触压力数据的提取,如图4所示。可以看出最大接触压力值达到300 MPa以上,受到边缘应力集中效应的影响,整个接触表面的压力分布也均远大于理论计算结果。在忽略压力集中区域最大值的情况下,接触压力 均 值 为98.76 MPa,接触压力有限元分析与理论计算结果之间的偏 差 达 到41.9%。此时,套筒轴向位移产生的支反力RF对应的压出力值为32.89 kN,如图5所示,与理论计算压出力偏差达到47.1%。

图3 内链节配合表面接触压力局部分布云图
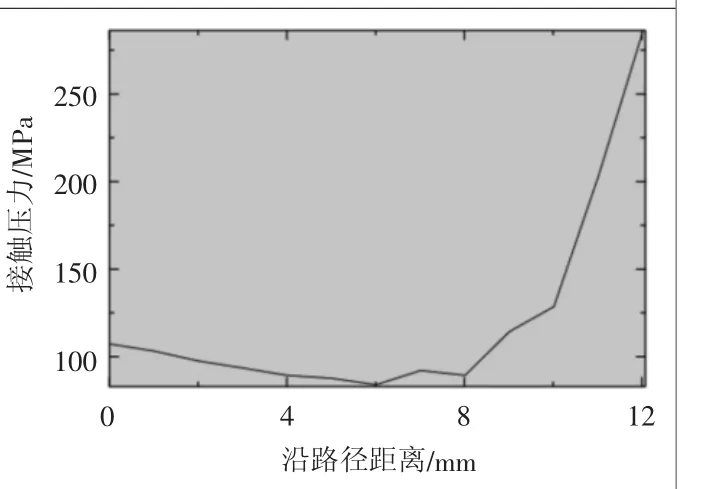
图4 内链节配合表面轴向接触压力结果

图5 内链节压出力
由上述分析可以看出,考虑边缘应力集中效应的情况下,理论计算结果将远小于有限元分析结果。同理,严格按照弹性力学理论进行链节过盈配合设计,设计过盈量将远大于实际所需的过盈量。因此,针对链条过盈量设计而言,常规的理论计算是不科学也是不合理的。
3 链条压出力理论计算的优化
由ABAQUS有限元计算结果表明,有限元计算与理论计算差距达到40%以上,前者考虑了边缘应力集中效应的存在,与实际配合状态更加吻合。若严格按照弹性力学理论进行链节过盈配合设计,设计过盈量将远大于所需过盈量,链板内孔周围的残余应力随之增大,将会大大降低链条整体的疲劳寿命。
因此,为了降低理论计算的误差,弥补边缘应力集中效应的影响,在运用链条压出力计算原理时,结合有限元分析,引入应力集中影响系数k,过盈配合接触表面之间产生径向结合压力Pi为

其中,k取值范围可取1.4~1.6,过盈配合框架组装精度较高时,取较大值。
引入应力集中影响系数后,内链节接触压力理论计算结果为97.41~111.33 kN,压出力的理论计算结果为31.30~35.78 kN。理论计算与有限元分析结果之间的接触压力误差降为1.4%~11%,压出力误差降为2%,两者的结果趋于一致,较优化前的结果误差有明显改善。为了验证该方案的通用性,对外单节进行同样的有限元分析。
ABAQUS计算的外单节配合面之间的接触压力局部分布云图(如图6)可以看出,销轴表面与外链板内孔接触区域的两端边缘处同样存在明显的边缘应力集中现象,接触压力呈现两端高、中间低的近似对称分布,沿轴向路径的接触压力结果如图7所示,在忽略两端压力集中区域最大值的情况下,接触压力均值 为 271.46 MPa,销 轴 轴向位移产生的支反力RF对应的压出力值为71.47 kN。

图6 外链节配合表面接触压力局部分布云图

图7 外链节配合表面轴向接触压力结果
在应力集中影响系数k取1.5时,理论计算接触压力为263.15 MPa,压出力为78.6 kN。有限元与优化后理论计算之间的接触压力结果误差约为3.2%。压出力误差约为10%。因此,引入应力集中影响系数后的理论计算方法,大大降低了与有限元分析之间的误差,且在链条的内链节和外链节之间具有通用性。
4 试验验证
为验证优化后理论计算结果的有效性,利用YAW-150压力试验机分别对上述规格链条的内、外链节各4件试样进行压出力数据实测,如图8所示。试验结果如图9所示,内链节压出力试验均值35.13 kN,与理论计算均值偏差约为4.7%,外链节压出力试验均值为84.66 kN,与理论计算均值偏差约为7.4%,理论计算与实际试验结果具有很好的吻合性,进一步证明了理论优化的合理性。

图8 压出力试验
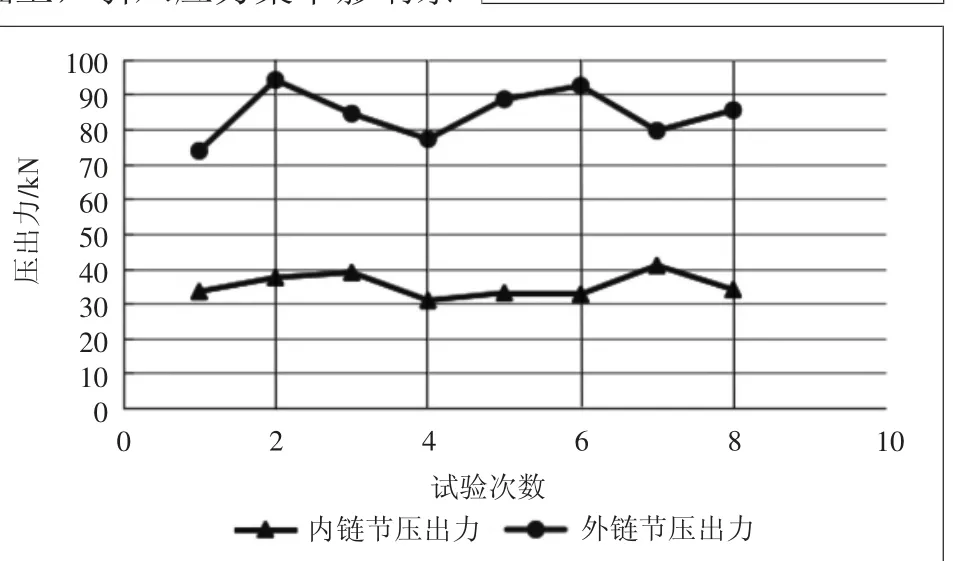
图9 压出力试验结果
5 结论
1)在基于ABAQUS过盈接触表面应力分布的分析基础上,引入应力集中影响系数,弥补了用弹性力学理论进行链条联结牢固度计算的不足,大大降低了理论计算的误差,提高了设计计算的准确性。
2)结合实例对优化后的理论计算方法进行了试验验证,结果一致性较高,证明了该优化方法是有效的,同时为链系统联结牢固度的计算提供了一种更加接近实际的理论计算方法。
