基于设计验算点拟合的响应面法可靠性分析

陈鹏，朱翊洲，谢永诚

（上海核工程研究设计院有限公司，上海 200233）

0 引言

传统的机械结构设计多采用确定性分析方法，所有变量及参数不考虑随机性和不确定性，为了保证在工程应用中的可靠性，通常在设计中考虑一定的安全系数以增加设计保守性。近年来，随着对设计精度和可靠性要求的不断提高，很多机械结构在设计中需要在考虑随机不确定性的基础上开展结构概率可靠性研究[1-2]。

不同于确定性结构分析，概率可靠性分析需要在概率分布的基础上开展更为复杂的统计学分析，因此需要计算效率较高的结构分析模型。目前工程中应用最为广泛的结构可靠性方法是以一次2阶矩法[3]为基础的1阶可靠性方法（FORM），该方法要求显式的结构失效功能函数，然而对于大多数工程问题，都难以直接给出以基本随机变量为变量的功能函数，如压力容器断裂失效，螺纹局部疲劳失效等。当结构形式复杂时，基于ANSYS等有限元模型开展Monte-Carlo数值实验[4]被认为是精度最高的结构可靠性分析方法，但当结构规模较大时，大量的数值实验需要仿真时间难以估量的模拟实验。

为了提高求解效率以适用于工程分析，对于复杂的机械机构，目前使用最多的是用响应面法对真实失效曲面进行拟合，由于真实失效曲面的复杂性，在全域拟合得到精度较高的近似失效曲面是不现实的，传统响应面法在各随机变量均值点附近开展拟合实验，当真实失效曲面非线性程度不高时，可以得到精度较高的拟合失效面和结构可靠度，但对于大多数结构可靠性问题，基于均值点拟合的响应面只能保证均值点局部的曲面近似精度。为了提高拟合精度，需要在真实失效曲面上的失效点局部区域进行拟合实验，而真实失效点通常只能够通过大量迭代不断逼近，对于复杂问题，计算效率并不高。

本文基于复杂结构的确定性有限元模型和响应面法，拟合得到结构失效的近似功能函数，根据1阶可靠性方法中的设计验算点法计算结构失效的近似验算点，并在该点局部区域重新开展近似实验得到基于设计验算点的结构响应面功能函数，在此基础上根据矩法计算结构可靠度，通过数值仿真和基于ANSYS的Monte-Carlo实验结果，验证了本文方法的计算精度。

1 基于响应面法的功能函数拟合

对于工程中的结构可靠性问题，描述结构失效的功能函数通常可以表示为

式中：S为基于相关强度理论和设计规范的设计应力强度值；σ为根据失效模式定义的目标应力值；x为影响应力分量σ的所有随机变量，当S也是随机变量时，功能函数对应的基本随机变量x应包含S。

在工程中，对于大多数结构都无法给出目标应力分量σ的显式表达式，更多的只能采用有限元等复杂的求解方法。对于结构可靠性问题，要得到结构失效概率或可靠度，通常需要显式的功能函数，因此基于多种多项式近似的响应面法得到了广泛应用，其中应用最多也最可靠的是Bucher不含交叉项的响应面形式：

其中，H为试验点系数矩阵。

在可靠性分析中，基本随机变量在每个点的分布概率均不相同，为保证在真实失效曲面附近和变量分布概率更高的区域拟合精度更高，本文采用加权最小二乘法进行拟合，权重矩阵和每个实验点的权重可以分别表示为：

其中，wi为权矩阵W中的对角元素。

对于工程中大多数有限元问题，当非线性程度较低时，在各基本随机变量x¯i±3δxi范围内拟合的超曲面精度都是可以接受的，因此响应面法也在ANSYS可靠性分析模块等商业软件中得到广泛应用。

对于大多数结构可靠性问题，基本随机变量均值点都不会在真实失效曲面上，因此在均值点附近拟合得到的响应面都有较大的误差，尤其是可靠度较高、功能函数非线性较高的可靠性问题。

经典响应面法认为，第一次围绕均值点选取实验点拟合出响应面后，再采用式（6）进行迭代，可保证算出的实验点中心近似落在真实失效面上。

式中：μ为均值点；xD为设计验算点。

这种方法尽管可以得到相对较高的计算精度，但对于复杂结构问题，迭代过程难以实现且效率较低。

2 基于设计验算点的可靠性方法

由于基本变量平均值不在极限状态曲面上，随着均值点到极限状态曲面距离的增大，展开后的线性极限状态面可能较大程度地偏离原来的极限状态曲面。对于这一问题，采用验算点一次2阶矩法可以解决，即在极限状态曲面上选取一个最大可能失效点P*，并在该点处进行Taylor展开。

首先，设计验算点需要满足状态函数：

其中，μxi和σxi分别为基本变量xi的均值和标准差。

定义可靠性灵敏度系数αi：

1阶可靠性方法中假定结构功能函数的分布为正态分布，可利用功能函数的均值和标准差计算得到可靠度指标，即2阶矩可靠度指标。然而对于工程中大多数结构可靠性问题，基本随机变量和功能函数可能并不服从正态分布，需要考虑更高阶分布参数，在统计学中认为前4阶中心矩即可描述一个随机变量的大部分分布信息。

在高阶矩可靠性方法中，可以采用Edgeworth级数法[5]和点估计法[6-8]得到功能函数前4阶矩μg、δg、α3g、α4g，一种可行的功能函数标准正态化变换方法是Ono和Idota提出的高阶矩标准化方法（HOMST），即假定存在多项式变换：

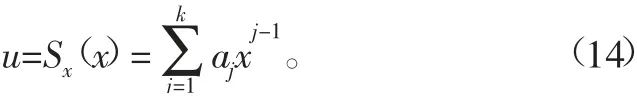
其中，aj是待定系数，通过计算Sx（x）的有限阶中心矩，分别得到等于标准正态分布u的对应阶中心矩。当考虑功能函数4阶矩时，将功能函数的标准化变量通过如下关系式表示为标准正态变量：

在本文结构可靠性方法中，首先根据式（4）拟合得到均值点附近的响应面功能函数（如式（2）），再根据基于设计验算点的1阶可靠性方法得到该功能函数下的验算点，最后，以验算点为中心再次进行响应面系数拟合，得到本文提出的基于验算点拟合的响应面功能函数。尽管该验算点可能不在真实失效曲面上，但相对于均值点已经有较高的精度提升。对于非正态分布假设，本文采用点估计法计算功能函数前4阶中心矩。

3 仿真算例

对于核反应堆中控制棒驱动机构的承压壳体结构，在ANSYS中建立轴对称模型，其中局部结构如图1所示。在运行过程中，承压壳体主要承受内压P和步跃冲击载荷F的作用。本文对承压壳体的可靠性分析分别考虑承压壳体与顶盖贯穿件异种金属焊缝处的强度失效（评定截面ASN1），钩爪壳体中部强度失效（评定截面ASN2），以及棒行程壳体和钩爪壳体Canopy焊缝处的强度失效（评定截面ASN3）。

图1 CRDM承压壳体有限元模型和评定截面

考虑内压P、步跃冲击载荷F及材料设计应力强度Sm三个变量为随机变量，则3个失效模式一次薄膜应力可靠度的功能函数可以表示为

其中，x= ［SmP F］T为基本随机变量，假定所有随机变量均服从正态分布，分布参数如表1所示。

表1 各基本随机变量分布参数

用本文方法得到的近似验算点和验算点处的真实功能函数值如表2所示。

表2 近似验算点及真实功能函数值

从表2可以看出，本文在均值点响应面功能函数基础上得到的近似验算点处，真实功能函数值都接近于0，可认为都处于真实失效面上。

由于响应面功能函数有显式形式，采用Monte-Carlo仿真也能够有极高的效率。分别基于有限元模型进行5000次仿真，基于响应面功能函数进行107次仿真，得到3个失效截面可靠度，如表3所示。

表3 基于响应面和有限元模型的MC仿真结果

表3中，RSM_E表示基于均值点拟合得到的响应面结果，RSM_D表示本文基于近似验算点拟合得到的响应面结果，ANSYS表示在ANSYS中PDS模块得到的收敛可靠度，Error表示本文结果与ANSYS结果的相对误差。

可以看出，本文提出的基于近似验算点拟合的响应面与真实失效曲面更为接近，在计算可靠度时有更高的仿真精度。需要指出的是，由于有限元模型复杂，在ANSYS中用重要采样法进行5000次仿真需要约5 h的计算时间，而用近似响应面功能函数进行107次抽样仿真只需要数分钟时间，在精度相近的情况下计算效率提升明显。

当基本随机变量为非正态分布时，假定Sm服从Weibull分布（115.92,12.15），内压服从对数正态分布（2.83,0.1），步跃载荷服从正态分布（60 000,6000），用式(16)计算可靠度指标得到的4阶矩可靠度求解得到的截面可靠度如表4所示。

表4 4阶矩可靠度与MC法的对比

表4中，R_SM表示2阶矩可靠度指标计算得到的结构可靠度，R_FM表示4阶矩可靠度指标计算得到的结构可靠度，Error表示4阶矩可靠度与ANSYS中进行5000次Monte-Carlo仿真得到的可靠度间的相对误差。

从表4中可以看出，当基本随机变量为非正态分布时，用4阶矩可靠度指标计算得到的结果可靠度有更高的精度。

4 结论

本文针对结构复杂的可靠性功能函数，基于均值响应面法和设计验算点法，得到近似验算点，再通过近似验算点局部区域的响应面拟合得到精度更高的响应面功能函数。对于非正态分布的结构可靠性问题，基于4阶矩可靠度指标法计算的结构可靠度也有更高的精度，相对于传统Monte-Carlo方法，近似的结构失效功能函数也有更高的计算效率。对于工程中结构复杂且可靠度要求较高的结构可靠性问题，本文方法有很好的适用性和参考意义。