综合运用物理思维化解一道竞赛题中的连续积累问题

叶鸣扬 杜素峰

（南京师范大学附属中学树人学校，江苏 南京 210011）

“大同杯”初中物理竞赛是上海市初中物理学科最具权威性的物理竞赛活动，在华东地区乃至全国范围都有一定的影响力.近年来，笔者所在地区部分高中学校的中考科技特长生选拔考试以及教师荣誉称号认定的笔试考试中，仍会出现一些“大同杯”试题及其改编题.可以说，无论出于对学生学科拔尖的需要，还是出于对教师自我提升的需要，“大同杯”试题都是十分优质的学习研究材料.

分析“大同杯”中的经典赛题，不仅要有广博的物理知识，灵活的物理思维，还要兼备较强的数学功底.其中一些竞赛考题，涉及了对连续变化量进行积累的问题.对于物理教师来说，使用微积分知识是可以快速求解的.然而，初中学生却没有接触过微积分，教师在研究和讲授相关习题时，应注意转换思路，避免使用超前的数学知识.

1 原题

例题.（2016年上海“大同中学杯”初中物理竞赛复赛第8题）如图1所示，假设有一块长方体石块堵住了水的去路.设水的密度为ρ，石块的质量为m，石块的左右侧面为正方形，边长为a，宽度为b，石块与地面足够粗糙，不会滑动，水若能推倒石块，则石块的宽度b应该满足的条件是

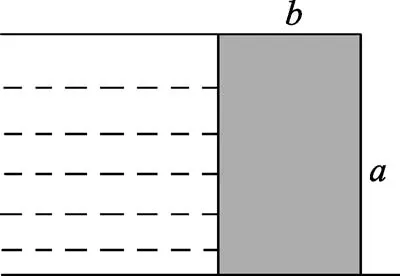
图1

2 本题解析及常见错因

2.1 本题解析

解决本题需要掌握3个核心知识点：

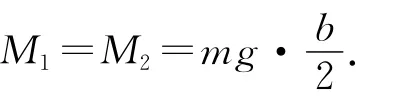
（3）水对石块的压力的等效作用点（以下简称为“压心”）位于石块高度处，即压力的力臂

综合上述分析，可以列出临界情况下的力矩平衡方程

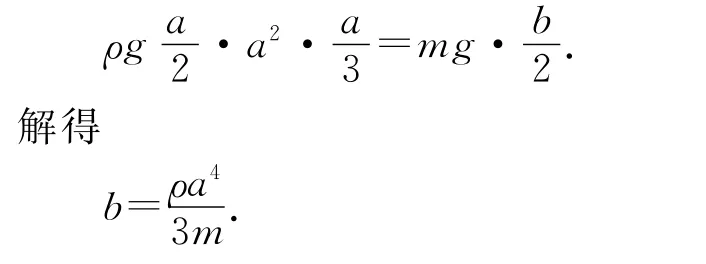
故本题应选（C）.

2.2 学生主要错因

笔者在校本物理思维拓展课程的教学中发现，学生普遍难以理解的关键在于知识点3.不少学生误认为水压的“压心”在处，于是得出临界时的力矩平衡条件

2.3 证明水压对竖直矩形受压面的“压心”在处

如图2所示，在距离水面h深处，取一极小深度d h，水在此处产生的压强为ρgh，受压面的面积为

图2

d S＝a·d h.

水对面积d S产生的压力为

d F＝p·d S＝ρgh·a d h.

以石块底端O点为支点，d F的力臂为d h到石块底部的距离，即a－h，故d F产生的力矩

d M＝d F·（a－h）＝ρgha（a－h）·d h.水对石块产生的总力矩为

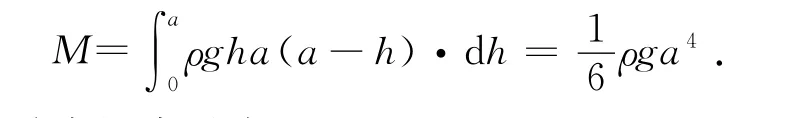
将总力矩表示为

3 综合运用思维方法证明“压心”位置为 a

3.1 寻找新思路

对初中学生介绍微积分方法，是十分不现实的.这其实是对教师提出了更高的要求，需要教师转变思路，深入思考，摸索出初中生能够理解的方法.

在分析非线性连续变化、连续累积等物理问题时，微积分无可替代.但在分析很多线性变化问题时，是可以通过无线分割、数形结合等思想方法转化为几何问题的.如高中阶段，匀变速直线运动的位移问题、弹簧弹力的做功问题等，都可以转化为与三角形相关的几何问题进行分析求解.

深入研究本题各变量的变化规律后不难发现，它们都是按照线性规律变化的：如图3所示，由液体压强分布规律以及力臂的定义得，自石块底部向上直至水面处，石块受到的压强由ρga均匀减小为0，而水压的力臂却由0均匀增大到a.这就给本题的积分问题转化为几何问题带来了可能.

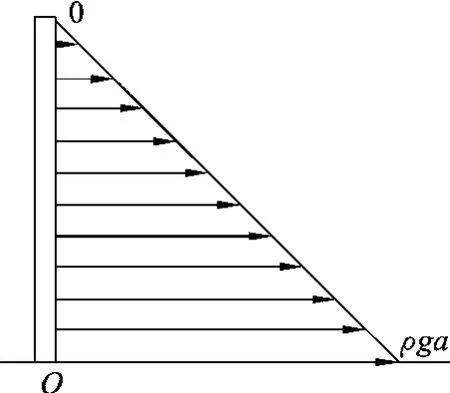
图3

3.2 运用类比方法进行建模

原情境中，水平方向的压力与“压心”问题，可以类比为初中学生更为熟悉的竖直方向的重力与重心问题.如图4所示，构建一个水平轻质杠杆OA，支点为O.自O点向A点依次悬挂材质均匀，宽度为Δh，长度均匀减小的细长小矩形.

图4

显然，自左向右每个小矩形的重力由ρga·Δh均匀较小到0，而每个小矩形的重力对于O点的力臂却由0均匀增大到最大值.力和力臂的变化规律，与例题中的水压问题十分相似.

3.3 运用无限分割思想进行等效

上一节的建模还不能完全等效例题中的水压情形，因为在每个细长小矩形的Δh内，重力并未发生变化.而例题中的水压是在发生连续不断的线性变化的.为了使细长小矩形的重力也逼近自O点向A点连续线性减小到0的规律，需要将细长小矩形无限细分下去.

小矩形划分地越细，整体图形就越趋近于三角形；当每一个小矩形都无限细分到Δh→0时，它们所构成的整体图形就是一个三角形了.

至此，原题寻找水压“压心”的问题，就等效转化为了寻找三角形重力力臂的问题.如图5所示，一块底为h的直角三角板可绕O点旋转，学生根据初中几何知识易得，三角形的重心P位于中线AC上，且AP＝2PC.所以三角板总重力G对于O点的力臂长为h.

图5

4 结语

对于学习过高等数学的中学物理教师来说，中学物理所需的微积分知识并不困难.但是教学活动是由相互依存的教和学两方面构成的，即使是物理竞赛辅导，也必须考虑到学生的发展阶段和理解能力，切不可把提升物理思维的良机变成灌输超前数学知识的过程.

遇到线性变化过程的累积问题，应当引导学生寻找变量的变化规律，转化到与变化规律相似的几何模型中进行巧妙求解.这样，既不增加学生的学习负担，又能发展学生多元的思维能力，才是研究物理竞赛题的意义所在.只有引导学生充分运用现有的知识，灵活运用分析问题的思维方法，才能促进思维能力的发展，达成解题素养的提升.