基于矩阵复原和暗通道理论的单色遥感图像去雾算法

刘纪伟， 王晓东， 李云辉

（中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033）

1 引 言

在遥感图像的成像过程中，大气云层和空气中的水汽、粉尘等悬浮粒子形成的雾霾通常会使目标物的反射光发生散射、被吸收、增加杂散光，造成图像对比度下降、细节丢失、色彩失真，从而降低图像质量。同时，在下传过程中，恶劣的工作环境使得遥感图像容易引入强噪声、丢失信息，由此得到信息不全的带雾遥感图像，影响地物目标的识别、分类、观测等。现有的图像去雾算法主要针对RGB三通道图像，而遥感图像多是全色单通道图像，且雾气分布呈白色，导致单色遥感图像去雾具有较高的挑战性。因此，针对单色遥感图像复原去雾的研究具有重要意义。

现有的图像去雾算法主要可以分为以下3类：（1）基于图像增强的去雾算法。根据图像的灰度分布，通过拉伸补偿对比度、亮度、色彩饱和度等突出图像的细节信息，提升图像的视觉观感，常用方法包括直方图均衡化、小波变换以及基于Retinex理论的算法等［1-3］。从另一角度而言，基于图像增强的算法又可分为全局增强和局部增强算法［4-7］，其中前者的主要作用是提升图像整体的对比度；后者针对图像的局部纹理特征，通过对图像的局部区域等细分单元进行变换处理，突出图像的细节特征，提升抗噪能力。（2）基于图像复原的去雾算法。可以分为两类，一类是基于先验统计信息，通过统计高低质量图像的亮度等信息，复原出高质量的无雾图像［8-9］。另一类是基于物理模型，研究相机成像过程中的大气扰动的影响，分析雾霾等引起图像质量下降的原因，构建相应的数学模型，以观测到的雾霾图像为输入，通过估算透射率等未知参数，反演计算复原出无雾图像［10-16］。由于依据的是大气散射机理模型，该类方法具有较强的鲁棒性，效果较为显著。（3）基于深度学习的去雾算法。近年来随着人工智能的发展，越来越多的研究人员使用深度学习的方法实现图像去雾，主要分为端对端和非端对端的网络模型。Dong等人提出了一种基于U-Net架构的多尺度特征融合去雾网络，成功恢复了高分辨率图像的空间信息［17］。Pang等人提出了一种双目图像去雾网络，通过左右两幅图像的相关性得到去雾损失函数，达到更好的去雾效果［18］。Zheng等人提出了多导向双边滤波卷积神经网络，实现了高分辨率4K图像去雾［19］。

综上所述，现有去雾算法多是针对特定场景下的彩色图像去雾，对于单色且可能存在信息丢失的遥感图像去雾研究尚不充分，因此本文提出了一种基于矩阵复原和暗通道理论的单色遥感图像复原去雾算法。为了解决图像在成像和传输过程中噪声过大和图像信息丢失的问题，首先采用交替方向乘子法（Alternating Direction Method of Multipliers， ADMM）对图像进行去噪复原，随后将去噪复原后的图像采用单色暗通道算法去雾，最后对实验图片进行主观评价，同时采用对比度、信息熵、峰值信噪比和结构相似性等指标进行客观评价。结果表明，与其他去雾算法相比，本文所提方法具有优越性。

2 ADMM方法及暗通道理论基础

2.1 ADMM方法

ADMM主要用于解决凸优化问题，引入一致性约束方法实现优化问题的解耦，将集中式问题并行求解，其主要思想是将原函数等价地分解成若干个可求解的子函数并求解全部子函数，然后通过协调全部子函数，从分块的数据集中获得相同的全局参数解，得到全局变量最优解［20-23］。

ADMM算法针对二决策域分块问题可以用如式（1）所示的表示方式：

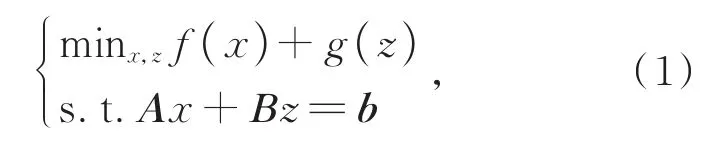
该表达式也被称为解耦约束式，其中x∈Rn，z∈Rm，x、z分别属于“x子函数”和“z子函数”，为共享变量，n与m可以不相等，即子函数的参数维度不同。A、B、b为共享变量的约束矩阵。将目标函数L(x，z，y)代入解耦约束式，可得：

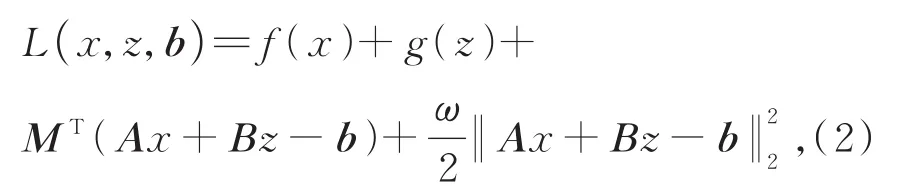
其中：M为乘子向量、ω为常数惩罚因子。由此其中一个子函数的一个共享变量作为未知变量，其余视为已知变量，便可得到全局迭代方程：

每完成一轮迭代，则更新乘子向量M，其迭代公式如式（4）所示：

最后根据实际问题，设置ADMM的收敛判据，其收敛判据的表达形式如式（5）所示：

其中：rk+1、sk+1为第k+1次迭代后的原始残差和对偶残差，ρ为对偶残差公式系数，εpri、εdual为两残差容忍最大值［24-26］。

2.2 暗通道理论基础

暗通道去雾理论最早由何凯明博士在2009年提出，他提出了一个基本假设，认为在绝大多数非天空的局部区域内，某一些像素点至少会有一个通道的灰度值较低，即比较暗的状态，由RGB三通道中取最小值组成灰度图，再对这张灰度图进行滤波，即暗通道去雾理论，其主要是基于如式（6）所示的物理模型：

其中：I(x)为去雾前图像，J(x)为理想无雾图像，t(x)为介质透射率，A为大气光成分。

何凯明博士对5 000多幅无雾图像进行统计，发现约75%的像素值为0，90%的像素值处于非常低的区间，由此提出暗通道理论，即对于一幅无雾图像，其暗通道可以表示为：

其中：Jc(y)为J的任意一个颜色通道，Ω(x)为像素点x处的窗口。根据暗通道理论，Jdark→0。

由式（6）和式（7）可以得到透射率的理想模型表达式如式（8）所示：

在现实生活中，无论多晴朗的天气，大气中的悬浮粒子也会是遥感图像产生一定的雾气的感觉，因此为在去雾的同时保留一定程度的自然效果，引入了一个［0，1］之间的模糊系数ω，ω通常取0.95，对理想透射率进行修正，即：

对于大气光值A，通常取暗通道图中亮度前1‰的像素，在原始雾图中取对应亮度最高的像素点灰度值作为大气光值A。

在实际处理图像的过程中，如果透射率值过低，会使得推导出的无雾图像偏白，因此要对透射率设一个下限值t0，t0通常取值为0.1，由此可得出无雾图像表达式如式（10）所示：

3 本文算法

现有图像去雾算法大多针对RGB三通道的图像。本文针对单色遥感图像去雾及其在传输过程中存在的噪声过大和信息丢失问题，在传统的暗通道理论基础上结合ADMM算法，实现了单色遥感图像的复原去雾。

遥感图像在成像和传输过程中存在的噪声、信息丢失及雾气干扰，可以解耦为去噪复原和去雾两个子问题。由此，可以将问题描述成如式（11）所示的形式：

其中：Y为信息丢失带雾图像，X为带雾图像，N为加性噪声。由上文给出的带雾图像成像过程可以得出：

则带雾图像X可通过最小化如下问题求得：

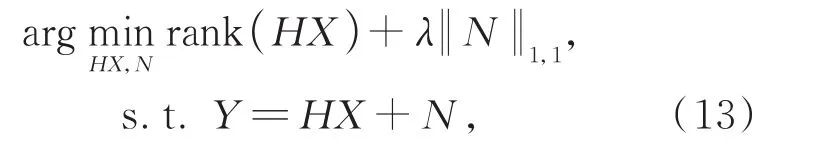
其中：rank（·）为矩阵的秩，λ为系数。由上文提到的ADMM的计算方法可以得出X，具体如式（14）所示：

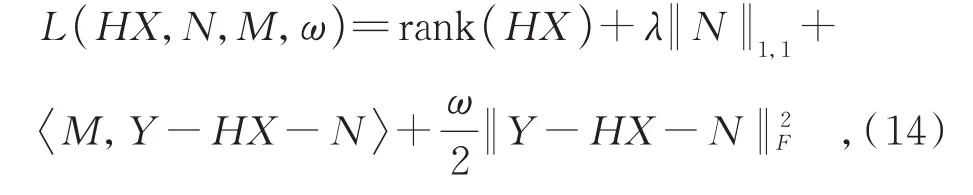
再由上文中暗通道理论的计算方法，可以得出：

本文的算法流程如图1所示。将单色遥感图像变换为三通道图像，采用基于ADMM的复原去噪算法进行去噪复原，将复原去噪的图像进行去雾处理。首先根据灰度值计算出灰度图像的暗通道值，随后根据计算结果估算透射率和大气光值，最后计算得到复原后的无雾图像。

图1 本文算法流程框图Fig.1 Flow chart of the algorithm in this paper

4 实验及结果分析

本文从长光卫星网站中分别选取了卫星和无人机遥感图像，选择多种不同应用场景，包括农田、城市、建筑、海洋、河流、山脊，验证本文算法的普适性和鲁棒性。分别进行了去雾实验、图像信息丢失去雾实验以及不同程度图像信息丢失去雾实验，验证方法的有效性。模拟雾图的成像机理，通过人工合成雾的方式得到带雾图像，然后对比原始图像、带雾图像及去雾图像的结果。

4.1 评价指标和对比算法

分别从主观评价和客观指标评价的角度与经典算法对比。本文根据算法应用场景，选取了基于图像增强的算法1、算法3、算法4、算法5以及基于图像复原的算法2、算法6作为对照，验证本文算法的优越性。本文选取的算法1为AGCWD（Adaptive Gamma Correction with Weighting Distribution），该方法通过伽马校正和亮度像素的概率分布来提高调灰暗图像亮度的自动变换；算法2为DCTSVD（Discrete Cosine Transform Pyramid and Singular Value Decomposition），该方法将低频子带图像的奇异矩阵与其全局直方图均衡化的奇异矩阵结合起来，估计均衡化后的低子带图像的奇异值矩阵，实现去噪和增强图像对比度；算法 3为GIHE（Gradient and Intensity Histogram），该方法将梯度引入强度直方图均衡化中，有效保护了图像的亮度信息，实现图像的去雾增强；算法4为IMSVD（Image Enhancement based on Singular Value Decomposition），该方法通过图像分解、可调对比度增强、降噪、图像合成4个步骤，结合亮度和颜色分量，有效实现了图像的去噪和去雾增强；算法5为RHESVD（Regularized-Histogram Equalization），该方法利用正则直方图均衡化和离散余弦变换来提高图像质量；算法6为 NPIE（Naturalness Preserved Image Enhancement），该方法利用高质量图像获取的先验多层亮度统计信息，有效实现图像去雾增强。选择的客观评价指标有对比度、结构相似性、峰值信噪比以及信息熵。

图像对比度计算公式为：

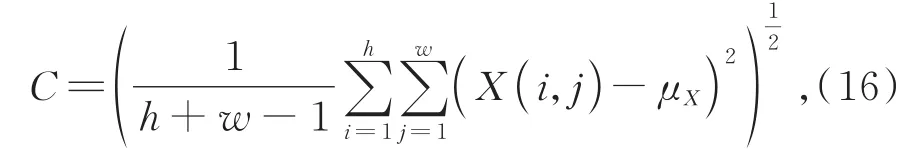
其中：h为图像的高度，w为图像的宽度，X(i，j)为图像的像素点，C为标准差，μX为像素灰度均值。

图像结构相似性计算公式为：

其中：l(x，y)为亮度比较，c(x，y)为对比度比较，s(x，y)为结构比较，SSIM为结构相似性。

图像峰值信噪比计算公式为：

其中：I(i，j)为无噪声原始图像，J(i，j)为噪声图像，PSNR为峰值信噪比。

图像信息熵计算公式为：

其中：p(i)为灰度值为i的像素所占比例，S为信息熵。

4.2 图像去雾结果对比

4.2.1 主观评价

对于7种不同算法进行去雾实验，对于带雾图像的去雾处理结果如图2所示。可以看出，算法1在多种场景下颜色偏亮，使得局部区域出现过度饱和，细节丢失；算法2在农田和城市两个场景下具有一定的去雾增强效果，但是在河流场景下，去雾效果并不显著；算法3去雾效果较为显著，但是存在着部分区域过亮；算法4可以有效增强对比度，提升视觉感知效果，但是整体色泽偏暗；算法5去雾效果不明显，图像依然存有薄雾效果；算法6有一定的去雾效果，但是从海洋去雾图中可以看出，图中依然存有微量雾气干扰；本文算法相较于其他算法，可以有效去除雾气干扰，较为彻底地去除整张图像中的雾气效果，在增强视觉感知效果的同时，尽可能地保留图像的细节。因此，本文算法普遍适用于多种应用场景。

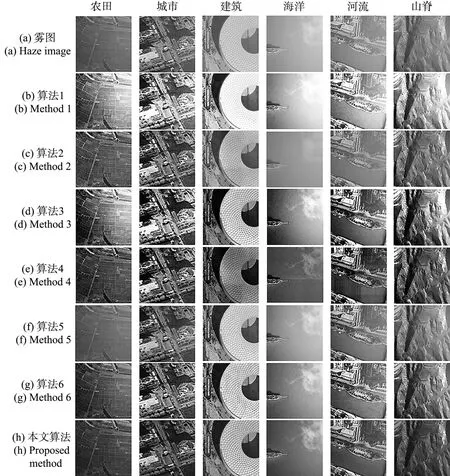
图2 图像去雾结果图Fig.2 Image dehazing result map

从上面的分析可以看出，算法3的去雾处理效果相对显著。图3为本文算法与无雾原图、带雾图像以及算法3处理结果的对比。可以看出，本文算法的处理结果与无雾原图基本可以保持一致，能够实现高效去雾。然而，算法3在图像右上部分的去雾结果偏亮，与原图差别较大。

图3 农田场景细节展示图Fig.3 Details of the farmland scene

4.2.2 客观评价

本文通过对比不同算法的峰值信噪比、结构相似性、对比度，客观评价图像去雾效果的优越性，计算结果如表1所示。结合主观评价结果，可以看出，算法1可以有效提升图像的对比度，但与原图像具有较差的结构相似性，图像细节信息丢失较为严重；算法2对图像的对比度提升并不显著，去雾增强效果不明显；算法3对图像的对比度增强较为明显，但在部分场景下，图像的结构相似性和峰值信噪比较差，算法适用范围具有局限性；算法4在多个评价指标中都有较好的表现，可以有效实现图像的去雾；算法5和算法6均能实现一定程度的对比度拉伸，实现图像的部分去雾，但与原图的结构相似性、细节信息存在差异；本文算法相对于原始输入雾图，6个场景的平均对比度提升14.748 9、平均峰值信噪比提升8.278 9，平均结构相似性提升0.149 1，在一定程度上有效提升了雾图的对比度，同时相对于原始图像具有极高的峰值信噪比和结构相似性，在提升视觉效果的同时，兼顾了图像的细节信息。

表1 图像去雾客观评价指标计算结果Tab.1 Calculation results of objective evaluation index for image dehazing

4.3 图像信息丢失复原去雾实验

模拟图像传输等引起图像信息丢失的过程，将人工合成雾图信息丢失30%，即随机将30%的像素值置为0，然后对原始图像、细节丢失带雾图像及复原去雾图像进行对比。

4.3.1 主观评价

图像信息丢失复原去雾的结果如图4所示，结合图2中的原始雾图，可以看出当图像信息丢失30%后，不同场景下图像的大部分细节信息丢失，很难从图像中捕获有用信息。从图4可以看出，算法1、2和算法4、5、6均不能有效去除噪声，复原图像的基本信息，实现复原去雾；算法3可以复原部分图像的细节信息，降低一部分噪声，去除原始雾图中的部分雾气，但其噪声干扰依然严重，视觉效果较差；对比图2中实验结果，本文算法可以有效地复原出绝大部分图像的细节信息，同时实现了图像有效去雾，因此具有很高的实际应用价值。

图4 信息丢失30%雾图复原去雾结果Fig.4 Restoration and dehazing results of 30% information loss haze image

4.3.2 客观评价

信息丢失遥感雾图的复原去雾主要是为了复原图像中细节信息，提升图像的应用价值，增强图像的视觉观感。因此本文选择信息熵以及对原始信息完整无雾图像的峰值信噪比和结构相似性来客观评价算法的复原去雾效果。

图像的复原去雾客观评价指标结果如表2所示。结合主观视觉效果，从计算结果可以看出，算法1、2、5、6的3个指标均未明显提升，图像复原去雾效果不显著；算法3的结构相似性有一定提升，恢复了部分图像细节，但是与原始图像依然有较大差距，信息恢复完整性较差；算法4的信息熵有小幅提升，但是结构相似性变化很小，图像信息恢复较少；本文算法相对于信息丢失30%的雾图，6个场景的平均信息熵提升1.665 2、平均峰值信噪比提升11.702 9，平均结构相似性提升0.814 6，均有明显提高，可以有效复原出原图像的细节信息，且与表1中信息完整雾图相比，本文算法可以实现有效去雾，图像结构信息更接近原始无雾图像。

表2 图像复原去雾客观评价指标计算结果Tab.2 Calculation results of objective evaluation indexes for image restoration and dehazing

4.4 不同比例图像信息丢失复原去雾实验

将带雾图像的图像信息分别保留50%、60%、70%和80%，使用本文算法对其进行复原去雾，将所得结果应用信息熵以及对原始信息完整无雾图像的峰值信噪比和结构相似性来客观评价本文算法在不同恶劣情况下的复原去雾效果，验证本文算法具有较宽的适用范围。

4.4.1 主观评价

对不同比例信息丢失的图像复原去雾结果如图5所示。可以看出，本文算法在图像信息不全，原始图像信息不同比例丢失的情况下，均可以有效复原出图像的主要信息，同时消除图像中的雾气分布。在仅保留50%图像信息的图像中，图像中的景物可辨识性极低，本文算法可以有效复原出图像中的大部分景物，同时相较于图中左侧信息完整的雾图，本文算法处理后的图像很好地去除了图中的雾气，提升了图像的视觉观感。

图5 不同比例信息丢失图像复原去雾结果Fig.5 Restoration and dehazing results of images with different proportions of information lost

4.4.2 客观评价

针对不同比例雾图信息丢失的复原去雾结果客观评价指标如表3所示。可以看出，在信息丢失20%的情况下，可以观测到的图像与原图的结构相似性也仅为0.035 4，峰值信噪比极低，信息熵较小，可辨识信息较少。通过本文算法处理后，信息丢失20%的输入图像相对于原图的结构相似性提升到了0.596 4，图像的信息熵和峰值信噪比也明显提升，可捕获信息明显增多，算法具有较强的复原去雾效果。

表3 不同比例信息丢失雾图复原去雾客观评价指标计算结果Tab.3 Calculation results of objective evaluation indexes for restoration and dehazing of fog images with different proportions of information loss

5 结 论

本文提出了一种基于ADMM矩阵复原和暗通道理论的单色遥感图像去雾算法，实现了信息丢失情况下的图像复原去雾。通过主观评价与客观指标分析相结合，综合评判信息完整和信息丢失情况下的图像去雾结果。对比了6种经典图像去雾算法在多场景下的去雾效果以及在不同比例信息丢失情况下的复原去雾结果，实验结果表明，本文算法对于信息丢失30%的雾图，6个场景的平均信息熵提升1.665 2，平均峰值信噪比提升11.702 9，平均结构相似性提升0.814 6，指标提高显著，具有较好的复原去雾效果，能够在去除噪声恢复原图像有用结构信息的同时，提升图像的视觉效果，有利于图像的观测和信息获取，同时证明本文算法具有宽适性和较好的鲁棒性。