基于人工免疫算法的里奥型液晶调谐滤波器优化设计
2023-02-17陈立新周茹心苏文正郑文彬孟雯雯张士元谢向生姚丽双
陈立新, 周茹心, 苏文正, 郑文彬, 杨 迎, 孟雯雯, 张士元, 谢向生, 姚丽双
(汕头大学 理学院, 广东 汕头 515063)
1 引 言
液晶可调谐滤波器(Liquid Crystal Tunable Filter,LCTF)被广泛应用于高光谱成像、光通信以及显示等领域,是一类基于液晶电控双折射和偏振干涉原理来实现目标滤波波长可电控调谐的滤波器,具有驱动电压低且易于精确调控滤波波长、损耗低、成本低、易于集成等优势。液晶可调谐滤波器的基本结构主要有Lyot型[1-2]和Solc型[3-4]等。Solc型液晶滤波器是在一对平行或者正交偏振片中插入相同厚度、不同方位角的液晶滤波片所组成的,具有透过率高的优点,但其需精密的结构固定。相较而言,Lyot型滤波器具有结构简单且调谐范围宽的优点。一般的单级Lyot型滤波器由一对平行偏振片和一个光轴与偏振片透射方向成45°角的液晶滤波片组成[5-6],通过级联多个单级Lyot型实现窄带输出,同时调控对应级次的电压实现特定延迟量组合输出不同的中心波长。
对于多级Lyot型LCTF的设计,传统的设计方法是依据所需中心波长的半高宽和自由光谱范围(Free Spectral Range, FSR),从而确立多级LCTF的液晶盒厚度选取[7-9]。首先确定第一级和最后一级液晶滤波片的器件厚度,然后根据各级相位差为δn=2δn-1的线性要求,逐次确定中间级液晶滤波片的厚度。传统的液晶滤波器要求每级的相位差严格符合成等比例的关系,如此便会导致最后几级液晶滤波片器件厚度较厚,较难匹配光谱快速调谐的应用[10-11]。因此,本文开发了一种在液晶滤波片厚度、级数的选择上更加灵活的Lyot型LCTF优化设计方法,基于人工免疫算法(Immune Algorithm,IA)[12-13],根据多目标的特定滤波光谱效果来智能调控每一级液晶滤波片的厚度和驱动电压,从而实现特定滤波光谱性能。该方法可为Lyot型LCTF的实际设计、制作和性能调试提供理论指导。
2 LCTF光谱性能表征参数
Lyot型LCTF的光谱性能可以用静态参数和动态参数来共同表征。静态参数描述在一定光谱范围内滤取中心波长的光谱性能,其主要光谱评价参数如表1所示。LCTF的动态参数是指动态调谐过程中的精度控制参数,用于评价滤波器动态调谐的波长误差,其主要评价参数如表2所示。

表1 Lyot型LCTF的静态表征参数Tab.1 Static characterization parameters of Lyot type LCTF

表2 Lyot型LCTF的动态表征参数Tab.2 Dynamic characterization parameters of Lyot type LCTF
3 Lyot型LCTF优化模型优化算法的实现
对于多级Lyot型LCTF的优化设计问题,从数学角度可以将其描述为多参数调控的多目标优化问题。具体来说,就是以上述LCTF的多个性能参数的设计要求为目标,寻找与预设LCTF光谱性能最接近的每一级液晶滤波片厚度和驱动电压组合的最优解。为此,我们将多目标人工免疫算法运用到LCTF的优化设计研究中。多目标人工免疫算法是根据生物免疫系统演化而来的智能优化算法,具有良好的全局优化功能,正好匹配本文的Lyot型LCTF的多目标优化问题,因此可以基于人工免疫算法全局寻优来确定最接近理想光谱输出的Lyot型LCTF结构参数设置方案。
本文基于IA算法的LCTF的优化流程图如图1所示。

图1 基于人工免疫算法的LCTF优化流程图Fig.1 Flow chart of LCTF optimization based on artificial immune algorithm
IA算法优化LCTF的具体步骤如下:
(1) 建立LCTF滤波模型
首先建立液晶指向矢空间分布模型,根据在不同驱动电压下液晶器件内部不同位置处的倾斜角和扭曲角得到特定电压下液晶器件的有效双折射率值[14-15],从而可以推算出不同驱动电压下的液晶器件开态琼斯矩阵,用于后续LCTF光谱性能的计算[16-19]。
(2) 设定多目标光谱优化的判定规则
(i) 待滤取的中心波长无偏差且中心波长处的透过率最大,即λactual=λideal且Tactual(λ)=1,其中λactual、λideal分别表示所设计的LCTF实际滤取中心波长和理想滤取中心波长。
(ii) 透射主峰的半高宽(Full Width at Half Maximum,FWHM)值最小或等于预先设定的理想半高宽值,即min(FWHMactual) or FWHMactual=FWHMideal。
(iii) 透射主峰以外的杂峰抑制较好,具体为透射主峰以外的透过率最小,即min其 中Tactual(impurity peak)代表透射主峰外的杂峰透过率值。
(3) 利用人工免疫算法进行LCTF全局参数优化。
(i) 初始化液晶滤波片厚度与驱动电压
初始化种群,随机产生多个第一代子群体,针对每一级液晶滤波片厚度和驱动电压采用全局随机取样机制产生各自子群体的第一代,种群规模维度与液晶滤波器级数一致,即d=[d1,d2,...,dn]、V=[V1,V2,...,Vn],对于液晶滤波片厚度的约束条件为d1≤d2,d3,d4,...,dn-1≤dn,其中n为液晶滤波器的级数。
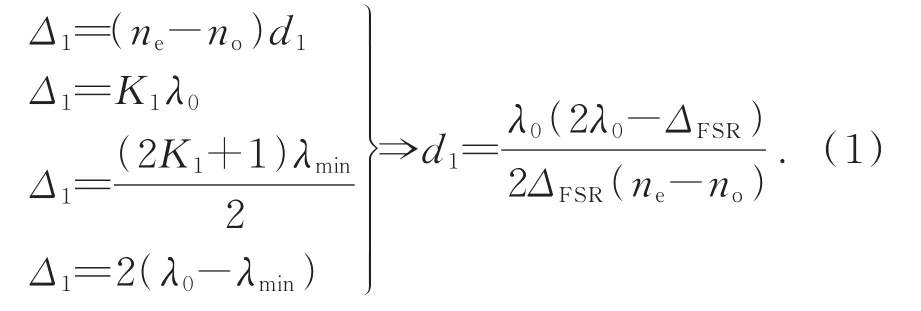
厚度最薄一级的相位延迟量Δ1决定了LCTF系统的自由光谱范围ΔFSR,因此d1可以根据所需ΔFSR计算得到,具体如式(1)所示。
而滤波片厚度最厚一级的相位延迟量Δn决定了LCTF系统透射主峰的半高宽ΔFWHM,因此dn可以根据所需ΔFWHM得到,具体如式(2)所示。
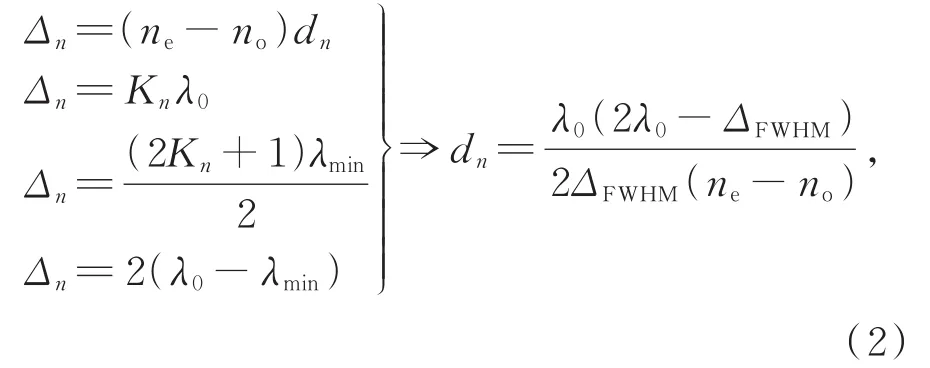
其中:K1、K2表示LCTF液晶滤波片厚度最薄一级和最厚一级的干涉级次,λmin表示距离中心波长λ0最近的一个波谷对应的波长。
(ii) 计算亲和度来进行抗原识别
亲和度也就是评价函数,是用来评价所设计滤波器的滤波效果的指标。在本文中,评价函数采用所设计的滤波器在可见光波段的光谱响应曲线与理想的滤波器光谱响应曲线之间的均方误差(Mean Square Error, MSE)来表示,具体如式(3)所示。
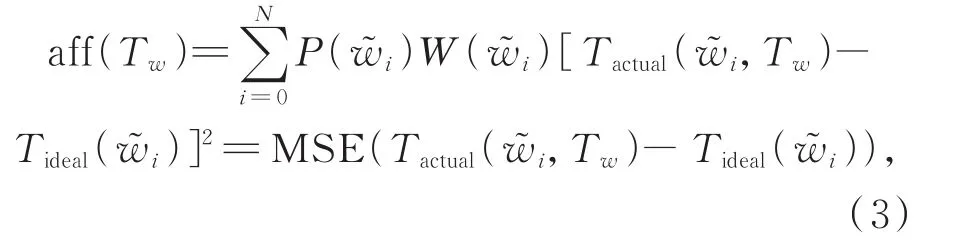
其 中 :P()用于控制中心波长的透过率;W()由通带权重w1与阻带权重w2构成,w1控制着Lyot型滤波器系统透射主峰的透过率与半高宽,w2控制着除透射主峰之外的整体杂峰影响,选取合理的通带与阻带权重比w1:w2可以保证在一定光谱内实现高透主峰以及旁瓣抑制的滤波效果。
(iii) 判断是否满足结束条件
对液晶滤波片厚度、驱动电压种群初代每一个抗体(可行解)进行亲和度函数判定,当所设计的滤波曲线达到了预期最优解时,此算法终止;否则,继续寻找参数以获取最佳滤波曲线。
(iv) 抗体激励
液晶滤波片厚度、驱动电压初代种群根据亲和度函数来筛选优质可行解抗体进入免疫循环处理,使其朝着理想滤波曲线趋势不断激励种群中的抗体。
(v) 免疫循环处理
对进入免疫系统的液晶滤波片厚度、电压抗体进行克隆复制,然后执行变异操作,即液晶滤波片厚度、驱动电压两种群突变产生新的可行解,以此来使设计滤波器的滤波曲线不断局部逼近预期滤波曲线,保证了抗体的多样性同时也加强局部优化能力。
(vi) 种群刷新
利用随机产生的新抗体来淘汰不符合理想滤波输出的液晶滤波片厚度、驱动电压种群劣质可行解的抗体,同时保留优质可行解,进而刷新液晶滤波片厚度、驱动电压新种群,然后再转步骤(3)中(ii)继续执行优化过程。
4 Lyot型LCTF优化设计
4.1 确定亲和度表达式中的参数
由于LCTF滤波模型中滤波曲线的通带与阻带是相互制约的,若通带权重w1过大,即过度追求透射主峰的半高宽和中心波长的透过率性能,则会出现旁瓣杂峰的陡增;若阻带权重w2过大,即过度追求旁瓣抑制性能,则透射主峰的透过率变低同时半高宽变宽。基于此,我们应合理选择通带与阻带的权重比,以获得较为理想的滤波曲线。
本文结合Matlab模拟在一系列的通带与阻带权重(w1∶w2)下,利用IA算法优化传统5级Lyot型LCTF,以此确立最佳的通带与阻带权重值。为了表征 LCTF滤波性能[20-21],本文主要以 FWHM、峰值旁瓣比(Peak Side Lobe Ration, PSLR)、峰值旁瓣电平(Peak Side Lobe Level, PSLL)、最大副瓣电平(Maximum Side Lobe Level, MSLL)等滤波参数,通过评价函数值来表征LCTF整体滤波性能,其定义为在同一中心滤波波长下,IA算法下Lyot型LCTF滤波光谱曲线与同等半高宽的理想矩形带通滤波曲线的均方误差(MSE)。
以400 nm为中心滤波波长,模拟得到基于IA算优化传统LCTF在一系列通带与阻带权重(w1∶w2)下的光谱曲线滤波性能对比图,如图2所示。

图2 不同通带与阻带(w1∶w2)权重下的滤波性能对比图。(a) 半高宽对比图;(b) 旁瓣抑制对比图。Fig.2 Comparison of filtering performance under different passband and stopband (w1∶w2) weights.(a) FWHM comparison; (b) Side-lobe suppression (SLS)comparison.
接下来得到不同通带与阻带的滤波性能参数对比结果,如表3所示。本文用评价函数值(MSE)来衡量整体滤波效果质量,得到不同权重与阻带权重下的评价函数值对比图,如图3所示。
由表3和图2对比可知,随着通带与阻带(w2/w1)权重值不断增大,半高宽、峰值旁瓣比、峰值旁瓣电平和最大副瓣电平均呈现先减小后增大的趋势,而且从图3的MSE值趋势发现,在w1=1、w2=25的通带与阻带权重比下,经IA算法优化传统Lyot型LCTF后的评价函数值取到极小值,图2的SLS对比图也表明此情况下较好地权衡了中心波长透射和整体杂峰的抑制。
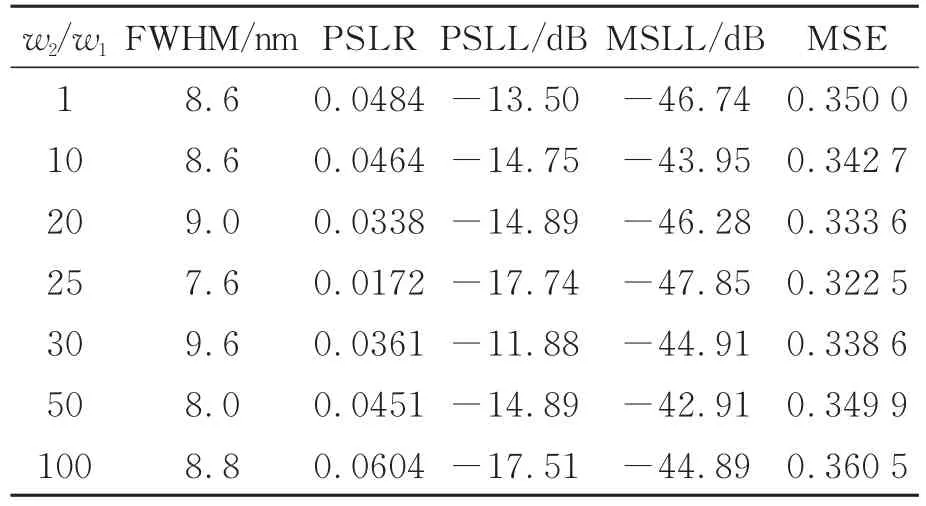
表3 不同通带与阻带权重比下的滤波性能参数对比Tab.3 Comparison of filtering performance parameters under different passband and stopband weight ratios

图3 不同通带与阻带权重下的评价函数值对比图Fig.3 Comparison of evaluation function values under different passband and stoppand weights
最后给出了在w1=1、w2=25的通带与阻带最佳权重比下,传统Lyot型LCTF经过IA算法优化的光谱曲线前后对比图,如图4所示。经过IA算法优化后,不仅FWHM由传统Lyot型的10 nm缩短至7.6 nm,提升了24.00%,而且PSLR由0.047 3降低至0.017 2,提升了63.63%,PSLL提升了31.49%。在IA算法优化后,虽然在远离主透射峰的旁瓣抑制不如Lyot型,但是整体滤波SLS相对于主透射峰均低于1.72%,因此保证了良好的单波长的滤波效果。

图4 IA算法优化传统Lyot型的光谱曲线前后对比图Fig.4 Comparison of spectral curves of traditional Lyot type before and after optimization by IA algorithm
4.2 通带与阻带权重比优化后的LCTF优化设计仿真
在传统的Lyot型滤波器的设计中,一般使每一级的相位差满足δn=2δn-1,故液晶盒的厚度一般设定为成比例,例如对于6级Lyot型LCTF,液晶盒的厚度一般为 2,4,8,16,32,64 μm。
可以看出,随着滤波器级数的增加,最后几级液晶盒的厚度会变得较厚,不利于快速响应的实现。因此,本文在液晶滤波片厚度和驱动电压任意的情况下通过算法寻找其最佳配置。在滤波器获得较为理想的光谱输出时,尽可能选择厚度较薄的液晶滤波片进行多级滤光片的组合,适应快速调谐的应用。
4.2.1 特定中心透射波长下旁瓣抑制的优化设计
以设计一个中心波长为500 nm的5级Lyot型滤波器为例,液晶滤波器片厚度取值范围为d1=2 μm≤d2、d3、d4≤d5=32 μm,设定中心波长半高宽为14 nm,基于IA算法设计的双种群LCTF与传统Lyot型LCTF的光谱响应曲线如图5所示。
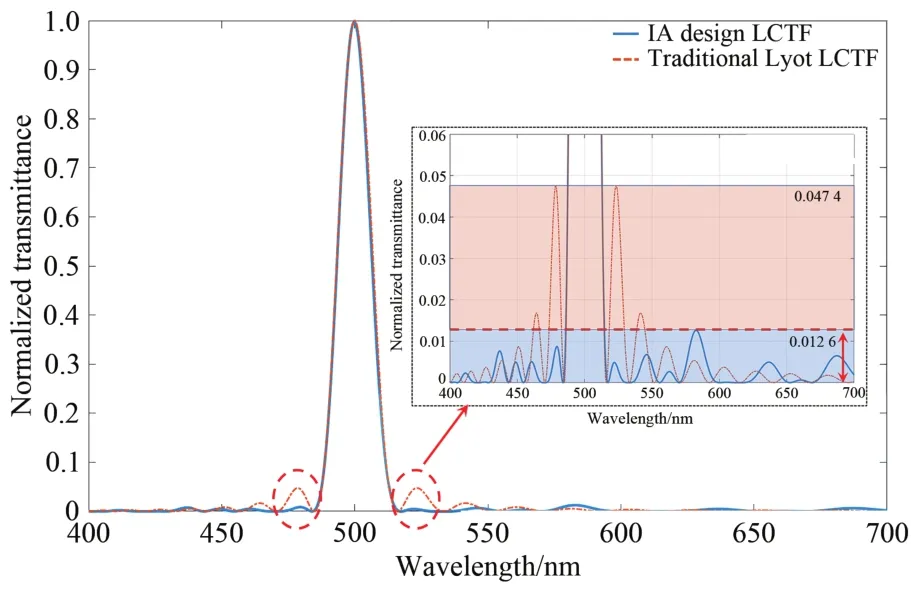
图5 IA算法设计的双种群滤波器(2.71,6.35,14.92,23.60,27.49 μm)与传统 Lyot型 LCTF (2,4,8,16,32 μm)光谱响应曲线对比图。Fig.5 Comparison of spectral response curves between dual population filter (2.71,6.35,14.92,23.60,27.49 μm) designed by IA algorithm and tranitional Lyot type LCTF(2,4,8,16,32 μm).
进而根据透过率得到相对应的传输增益值,即10lgT,得到IA算法设计与传统Lyot型LCTF传输增曲曲线对比图如图6所示。因此得到IA算法优化与传统Lyot型LCTF下的滤波性能参数的比较结果如表4所示。
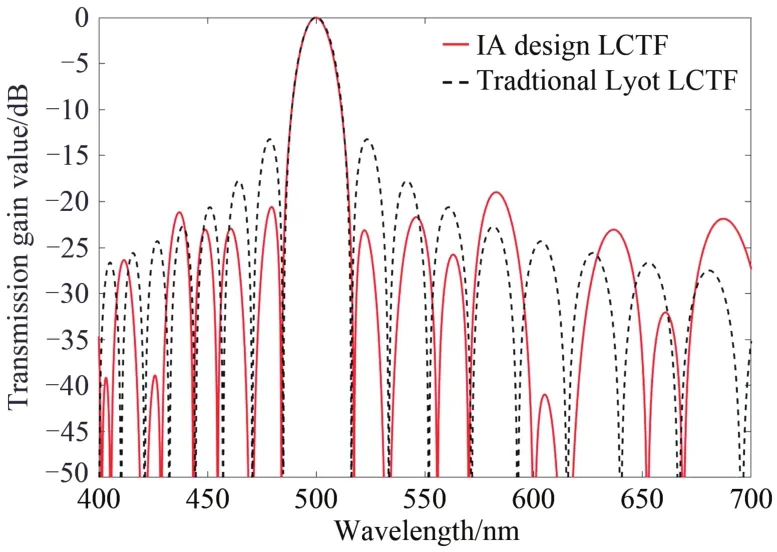
图6 IA算法设计的LCTF与传统Lyot型LCTF的传输增益曲线对比图Fig.6 Comparison of transmission gain curve between traditional Lyot type LCTF and LCTF design by IA algorithm

表4 传统Lyot型滤波器与IA算法设计下5级任意厚度滤波器的对比Tab.4 Comparison between traditional Lyot type filter and the five-stage filter with arbitrary thickness designed by IA algorithm
由图5可知,IA算法LCTF的SLS区域抑制在1.26%以下,而传统Lyot型的SLS区域抑制在4.74%,SLS明显改善,提升了276.19%。结合图5和表4的数据对比发现,IA算法设计的双种群滤波器的PSLR(0.047 4)相比于传统Lyot型滤波器(0.012 6)提升了73.42%。图6显示经过IA设计后,PSLL由-13.23 dB降低至-23.14 dB,提升了42.83%。从评估函数值来看,传统Lyot型滤波器的MSE值为0.395 8,IA算法设计的LCTF为0.340 8,其整体滤波性能相对提升了13.90%。综上所述,相比于传统Lyot型滤波器,IA算法设计的液晶滤波器可以较好地抑制截止区旁瓣,较好地提升了滤波性能。
4.2.2 特定中心透射波长下光谱分辨率的智能调控
在实际应用场景中,可以根据实际应用需求来设定中心波长的不同半高宽:选择宽带的情形下,可以增加来自带宽光源的光透过率;选择窄带的情形下,可以只滤取特定波长的光。
利用IA算法可以针对同一波长下的不同半高宽模拟对应滤波器的光谱响应曲线,如图7所示。
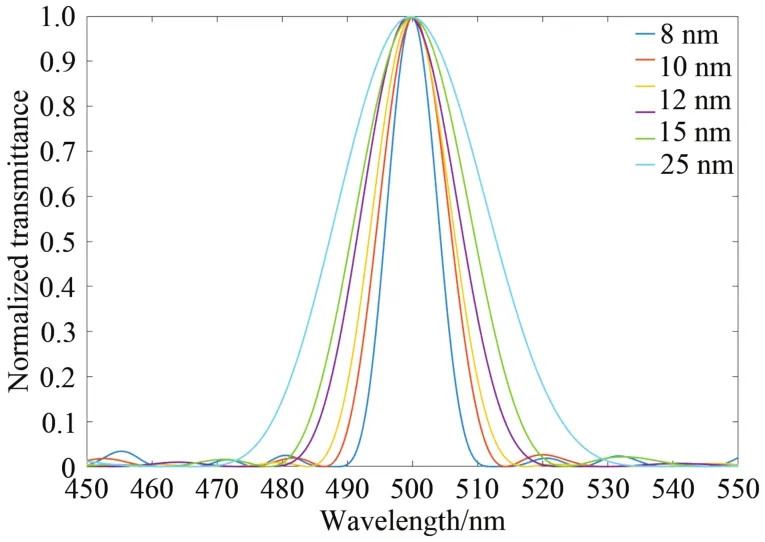
图7 不同半高宽设定下的光谱响应曲线Fig.7 Spectral response curves with different FWHM
4.2.3 不同中心透射波长的LCTF设计
考虑液晶的双折射率色散问题,即液晶的双折射率随波长而变化,现利用IA算法在设定不同中心透射波长的情况下设计双种群滤波器,得到的整体光谱响应曲线如图8所示。

图8 IA算法设计的实际LCTF与传统Lyot型LCTF下的整体光谱响应曲线对比图Fig.8 Comparison of the overall spectral response curves between the actual LCTF designed by IA algorithm and the traditional Lyot LCTF
进一步得到IA算法设计的实际LCTF与传统Lyot型LCTF在不同透射中心波长下的评价函数值对比图,如图9所示。
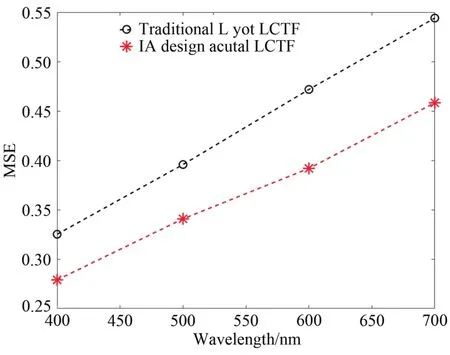
图9 IA算法设计的实际LCTF与传统Lyot型LCTF下的评价函数值对比图Fig.9 Comparison of the evaluation function values under the actual LCTF designed by the IA algorithm and the traditional Lyot type LCTF
由图9可知,IA算法优化设计的实际LCTF相比于传统Lyot型LCTF,在不同透射中心波长下,峰值旁瓣被明显抑制,而且整体滤波效果更佳,MSE值在各个波段分别提升了14.15%(@400 nm),13.90% (@500 nm),16.93% (@600 nm),15.80 (@700 nm),滤波性能平均提升了15.20%。
5 结 论
本文采用人工免疫算法优化了液晶滤波器的设计,即基于LCTF的滤波模型,通过优化LCTF的多目标光谱性能来合理选取LCTF的液晶盒厚度和驱动电压。该算法的核心是建立光谱响应曲线的评价函数,其中确定通带与阻带的权重比尤为重要。通过仿真发现,滤波器的各项滤波性能参数随权重比的变化呈现先减小后增大的趋势。当通带与阻带权重比为w1∶w2=1∶25时,利用IA在400 nm中心波长下优化传统Lyot型LCTF,FWHM提升24.00%,PSLR提升63.63%,可以较好地兼顾滤波器的半高宽与旁瓣抑制性能。
通过IA算法在液晶盒厚度任意的情况下实际设计了5级LCTF,并与传统5级Lyot型LCTF对比,在500 nm中心滤波波长下,SLS提升271.16%,PSLL提升73.42%,整体滤波效果提升了13.90%。因此通过IA算法来设计滤波器可以有效地保证LCTF滤波波长的透过率、半高宽以及抑制阻带的波纹大小,平均滤波性能提升了15.20%。与此同时,还可以针对滤波的不同调谐需求(特定波形、半高宽)结合IA算法进行优化设计。下一步,将考虑光学元件损失、LCTF斜入射情况以及液晶材料[22-23]等实际因素进行IA算法下的LCTF优化模型的完善改进。
