3S1–3D1 coupled channel ΛcN interactions:chiral effective field theory versuslattice QCD

Jing Song ,Yang Xiao,3 ,Zhi-Wei Liu ,Kai-Wen Li,4,5,∗ and Li-Sheng Geng,6,7

1 School of space and environment,Beihang University,Beijing,102206,China

2 School of Physics,Beihang University,Beijing,102206,China

3 Université Paris-Saclay,CNRS/IN2P3,IJCLab,Orsay,F-91405,France

4 Medical Management Department,CAS Ion Medical Technology Co.,Ltd,Beijing 100190,China

5 Beijing Advanced Innovation Center for Big Data-Based Precision Medicine,School of Medicine and Engineering,Beihang University,Key Laboratory of Big Data-Based Precision Medicine (Beihang University),Ministry of Industry and Information Technology,Beijing,100191,China

6 Beijing Key Laboratory of Advanced Nuclear Materials and Physics,Beihang University,Beijing,102206,China

7 School of Physics and Microelectronics,Zhengzhou University,Zhengzhou,Henan,450001,China

Abstract We study the lattice QCD ΛcN phase shifts for the 3S1–3D1 coupled channel using both the leading order covariant chiral effective theory and the next-to-leading order non-relativistic chiral effective field theory (ChEFT).We show that although it is possible to describe simultaneously the 3S1 and 3D1 phase shifts and the inelasticity η1,the fitted energy range is quite small,only up to Ec.m.=5 MeV.This raises concerns regarding the consistency between leading/next-to-leading order ChEFT and the lattice QCD simulations.

Keywords: ΛcN interaction,covariant ChEFT,lattice QCD

1.Introduction

The Λcbaryon as the lightest charm baryon has attracted a lot of attention,which may exist in finite nuclei to form Λchypernuclei.The HAL QCD Collaboration performed the first lattice QCD simulations of the ΛcNand ΣcNinteractions for unphysical light quark masses (mπ=410,570,700 MeV)[1],which provided vital information on the interaction between a nucleon and a charmed baryon Λcor Σc.Employing these lattice QCD results,extrapolations to the physical point have been performed using either the nonrelativistic chiral effective field theory (ChEFT) at next-toleading order (NLO) [2] or the covariant ChEFT at leading order(LO)[3].In the covariant ChEFT,Lorentz covariance is maintained by employing the covariant chiral Lagrangians,the full form of Dirac spinors,and the relativistic scattering equation (the Kadyshevsky equation).It has been shown that the covariant ChEFT approach can provide reasonable descriptions of octet baryon-octet baryon interactions already at LO,including all the systems from strangenessS=0 toS=-4,at least in the low energy region [4–14].8The next-to-next-to-leading order relativistic chiral nucleon–nucleon interaction is shown to be able to describe the neutron-proton scattering phaseshifts up to Tlab.=200 MeV as well as the next-to-next-to-next-toleading order non-relativistic chiral nucleon–nucleon interactions [15].A recent study[11]showed that one could reproduce both the physical1S0and3S1–3D1and the lattice QCD nucleon–nucleon partial wave phase shifts fairly well.In particular,for the physical nucleon–nucleon phase shifts and lattice QCD data atmπ=469 MeV,if one only fits to the3S1phase shifts,the3D1phase shifts and inelasticity η1can be predicted and vice versa,as shown in [16].It implies that indeed the correlations induced by the imposed constraint of covariance in the covariant chiral potentials is reasonable.

In our previous study of the ΛcNinteraction in the covariant ChEFT [3],the low energy constants (LECs) were determined by fitting to the lattice QCD data from the HAL QCD Collaboration,where theS-wave phase shifts up toEc.m.=30 MeV formπ=410 and 570 MeV were considered.The results showed that the covariant ChEFT can describe the lattice QCD data fairly well at low energies.In addition,the phase shifts of the ΛcN3D1partial wave and the inelasticity η1,as well as their physical counterparts were predicted.

In a recent study[17],it was shown that the predicted3D1phase shifts by the NLO non-relativistic ChEFT are in agreement with the lattice QCD data of [18] at higher energies,but not those of [3].A closer examination of the lattice QCD data revealed,however,that although at higher energies,the predictions of[3] do not agree with the lattice QCD data,but at low energies close to the threshold,they do agree,both for the3D1phase shifts and the inelasticity,at least qualitatively.On the other hand,the predictions of the NLO non-relativistic ChEFT [2]do not agree with the lattice QCD data at low energies.

In this work,we revisit the fits to the lattice QCD data and the corresponding extrapolations to the physical point.We study in detail the differences between the non-relativistic ChEFT and covariant ChEFT in the description of the ΛcN3D1phase shifts and inelasticity η1,including the effects of baryon masses andSDcoupling in the contact terms,and the retardation effects in the one meson exchange term.9We found that the retardation effects are quite small and therefore refrain from explicit discussions about these effects from now on,but they are always included in our study.In addition,we study extrapolations to the physical point employing different fitting strategies to the lattice QCD data.These results are important to better understand the ΛcNinteraction and might be helpful to guide future hypernuclei experiments.

The paper is organized as follows.In section 2,we briefly introduce the non-relativistic and the covariant chiral EFT.In section 3 we perform fits to the lattice QCD data of [18],focusing on the low energy region,where ChEFT is expected to work.We summarize in section 4.

2.Theoretical framework

In this section,we briefly introduce the non-relativistic ChEFT and covariant ChEFT for theYcNinteractions,whereYc=Λc,Σc,and highlight the differences relevant for the present study.

In the non-relativistic ChEFT,the next-to-leading order potentials consist of non-derivative four-baryon contact terms(CT) and one-meson-exchanges (OME).The CT potentials for the1S0and3S1–3D1partial waves are [19]

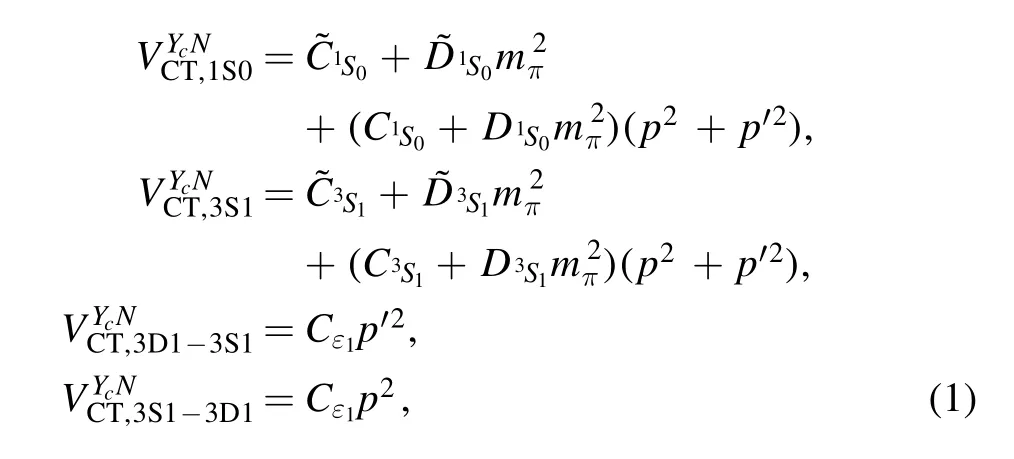
wherep=|p|andp′=∣p′∣are the initial and final center-ofmass (c.m.) momenta of theYcNsystem,respectively.Ci,Di(i=1S0,3S1,and ε1)are LECs that need to be fixed by fitting to either experimental or lattice QCD data.The OME potential reads,

whereq=p′ -pis the transferred momentum.The coupling constantsand the isospin factor I can be found in,e.g.[2,20].The scattering amplitudes are then obtained by solving the coupled-channel Lippmann-Schwinger equation

where ΛFis the cutoff whose value is in the range of 500–600 MeV.The partial waveSmatrix is related to the onshellTmatrix by

where pcmis the C.M.three-momentum of the ΛcNsystem.The phase space factorais determined by the elastic unitarity of the scattering equation.For single channels,the phase shifts δ can be obtained from the on-shellSmatrix

Table 1.Seven fitting strategies studied in this work,where ✓indicates that the SD coupling in the CT potential is turned on,while×denotes that the SD coupling is turned off in the covariant ChEFT approach.

In order to calculate the phase shifts in coupled channels(J>0),we use the ‘Stapp’-or ‘bar’-phase shifts parametrisation [21] of theSmatrix,which can be written as

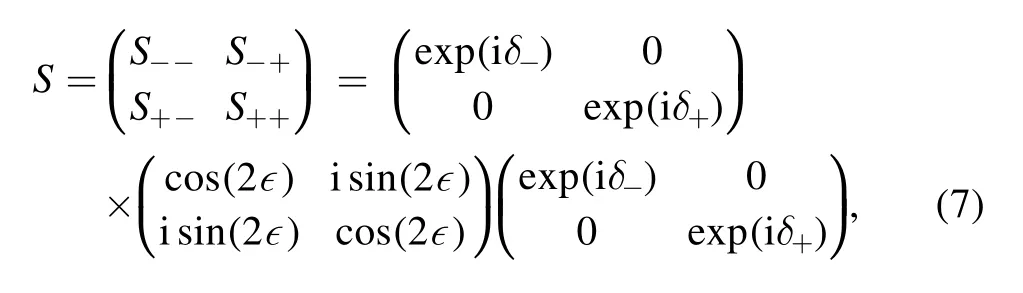
where the subscript ‘+’ isJ+1,‘-’ forJ-1.The resulting phase shifts and mixing angles are

For more details about the non-relativistic ChEFT,please refer to [2,17,19,20,22–31].

In the covariant ChEFT,as discussed in [3],the1S0and3S1–3D1CT potentials for theYcNsystem read,

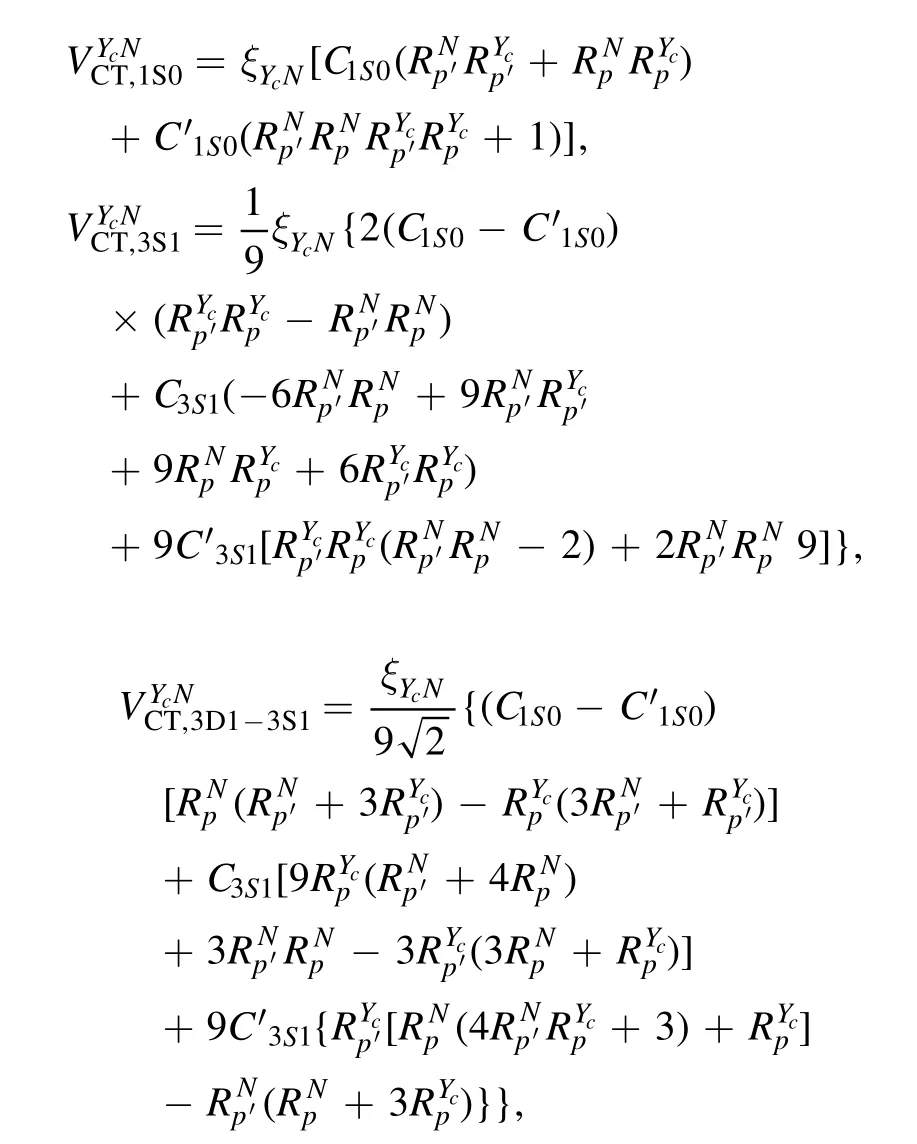
It should be noted that there exist three differences between the covariant and the non-relativistic ChEFT potentials as presented above: (1) the covariant chiral potentials explicitly contain the baryon massesMYcandMN,whereMYc=(MΛc+MΣc)2,whose values are the same as those given in table 1 of [3];(2) because of the factMYc≠MN,the LECs from the1S0partial wave also contribute to those of the3S1–3D1partial waves;(3) the LECs responsible for theSDcoupling are correlated with those of the1S0and3S1potentials.It should be noted that the contributions from the ΣcNintermediate state in the CT potentials were set zero in both the non relativistic ChEFT[2]and covariant ChEFT[3],since the limited lattice QCD data could not fix these contributions.

The leading-order OME potential reads

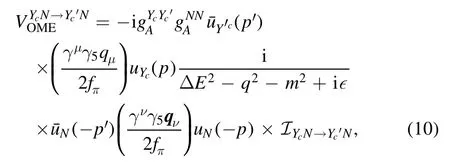
whereΔE=Ep′-Epis the transferred kinetic energy,i.e.the retardation effect,and we adopt the complete form of the Dirac spinor for the baryons involved

The coupled-channel Kadyshevsky equation[32]is solved to obtain the scattering amplitudes

3.Fitting procedure

In[33],the HAL QCD Collaboration presented the1S0and3S1phase shifts of the ΛcNinteraction obtained from lattice QCD simulations withmπ=410,570,and 700 MeV.In addition,the corresponding3D1partial wave phase shifts and inelasticity η1can be found in the PhD thesis of Takaya Miyamoto [18].The results show that the ΛcN3D1phase shifts forMπ=410,570,and 700 MeV are slightly repulsive for the center of mass energy no larger than 15,30,and 40 MeV,respectively and become attractive asEc.m.increases,and the inelasticity η1is close to unity in the whole energy region.Fittings to theSpartial waves ofmπ=410 and 570 MeV (withEc.m.≤30 MeV),and extrapolations to the physical point were performed in both the nonrelativistic ChEFT[2]and covariant ChEFT[3].The predictions for the3D1phase shifts and inelasticity η1turn out to be dramatically different.The3D1interaction in the former approach is attractive,while that in the latter is repulsive.In addition,both approaches predict aSDcoupling stronger than that shown by the lattice QCD data.

In this study,we first investigate where such differences in the predicted ΛcN3D1phase shifts between the two approaches originate.In particular,we focus on the masses ofYcandNand theSDcoupling in the CT potential.We note that there are no baryon mass terms in the CT potential of the non-relativistic ChEFT,whileMB(MYc,MN) appears in the baryon spinors of the covariant ChEFT.AsMYc≥MN,we used the‘physical’masses forYcandNin our previous study,which has the consequence thatC1S0(C′1S0) also contributes to the3S1–3D1partial waves[3].In addition,theSDcoupling in the covariant ChEFT is correlated to the3S1potential,while a free LEC appears in the non-relativistic ChEFT.These two differences lead to in total 22=4 combinations that will be examined.In addition to our previous study [3],we perform three more fits to the same lattice QCD data,and make a systematic comparison of the results,to better understand how the results depend on the baryon masses andSDcoupling in the CT potential.

Moreover,since both approaches fail to precisely reproduce the lattice QCD3D1phase shifts of ΛcNat low energies,we adopt a new fitting strategy where the phase shifts of ΛcN3S1,3D1partial waves and inelasticity η1withEc.m.≤5 MeV are simultaneously fitted.The new strategy can provide a closer look at the two approaches in the descriptions of low energy lattice QCD data.Note that we only consider the lattice QCD data withmπ=410 and 570 MeV in all the aforementioned fittings.Details of the fitting strategies in this work are shown in table 1.

4.Results and discussions

4.1.Origin of the difference in predicting the ΛcN 3D1 phase shifts

The fitted results of strategies 1–4 as described in the previous section are summarized qualitatively in table 2 and quantitatively in figure 1.It is noted that the treatment of the potentials in strategy 1 is that adopted in [3]10The χ2 shown in table 2 is larger than that in [3] because of different fitting strategies.The χ2 in [3] is obtained by fitting to the 3S1 phase shits,while the χ2 in table 2 includes the 3D1 and mixing angle data as well.,and strategy 4 is approximately the same as that of the non-relativistic ChEFT.The following conclusions can be obtained from the table: first,the baryon masses affect the3D1phase shifts for the large pion mass (mπ=570 MeV),where negative phase shifts are obtained in strategies 1,2 and they become positive ifMYcis taken to be the same asMN(strategies 3,4).Second,only whenMYc=MNand theSDcoupling in the CT potential is turned off,the3D1interaction becomes attractive in the unphysical region (strategy 4).Third,theSDcoupling in the covariant ChEFT reduces the attraction in the3S1partial wave in the physical region,compared with the non-relativistic case,as shown in strategies 1 and 3.

4.2.Simultaneous fits to the ΛcN 3S1–3D1 partial waves

In this subsection,we simultaneously fit to the phase shifts of ΛcN3S1,3D1and inelasticity η1of the lattice QCD data formπ=410 and 570 MeV with a smaller energy range from threshold up toEc.m.=5 MeV in order to achieve a χ2/d.o.f.≈1.With this new strategy,we aim to check whether the covariant ChEFT approach or the non-relativistic ChEFT approach can precisely describe the lattice QCD data at low energies,where they are believed to work the best.In the covariant ChEFT,we only consider two strategies: eitherMYc≠MNorMYc=MN.TheSDcoupling appears naturally in the CT potentials,therefore we did not manually turn it off.The non-relativistic ChEFT approach is also applied to perform the fits for comparison.The fitted results of strategies 5-7,as described in table 1,are qualitatively shown in table 3 and quantitatively shown in figures 2 and 4.

Figure 1.ΛcN 3S1,3D1 phase shifts and inelasticity η1 for different pion masses.The results are obtained by fitting to the lattice QCD ΛcN S—wave phase shifts for Ec.m.≤30 MeV.The bands are generated from the variation of ΛF from 600 to 700 MeV.Different labels denote the ΛcN phase shifts of strategies 1–4: ‘w/.’ is the abbreviation for ‘with’,and ‘w/o.’ is the abbreviation for ‘without’.

Table 2.Dependence of the ΛcN 3S1 and 3D1 phase shifts on the baryon masses and SD coupling for different pion masses(in units of MeV).The‘+’and ‘-’ indicate the sign of the ΛcN 3S1 and 3D1 phase shifts within the fitting region Ec.m.≤30 MeV,where ‘+’ and‘-’ denote attractive and repulsive potentials,respectively.The values of the χ2/d.o.f.(in units of 10-2) are obtained with ΛF=600/700 MeV.

Figure 2.Same as figure 1,but the results are obtained by fitting to the lattice QCD phase shifts of 3S1,3D1 partial waves and inelasticity η1 simultaneously for Ec.m.≤5 MeV.

Table 3.Phase shifts of ΛcN 3S1 and 3D1 partial waves for different pion masses based on the covariant ChEFT approach and non-relativistic ChEFT approach.The former depends on the baryon masses used,either physical or the lattice QCD MYc and MN or their average.These results are obtained by fitting to the phase shifts of 3S1,3D1 and inelasticity η1 simultaneously for Ec.m.≤5 MeV from lattice QCD simulations,and mπ is in units of MeV.The ‘+’ and ‘-’ indicate the sign of ΛcN 3S1 and 3D1 partial waves phase shifts within the fitting region,where ‘+’ and ‘-’ stand for attractive and repulsive potentials,respectively.The values of the χ2/d.o.f.are obtained with ΛF=600/700 MeV in the covariant ChEFT and ΛF=500/600 MeV in the non-relativistic ChEFT.

Figure 3.ΛcN 3S1,3D1 phase shifts and inelasticity η1 as functions of Ec.m..The results are obtained by fitting to the lattice QCD δ3S1,δ3D1 and η1 simultaneously up to Ec.m.≤5 MeV (blue bands) and Ec.m.≤20 MeV (magenta bands) in covariant ChEFT.

4.2.1.Covariant ChEFT.First,we study how the use of‘physical’ baryon masses affects the description of the ΛcNinteractions in the covariant ChEFT.The relevant fitting details and the corresponding values of the χ2/d.o.f.are summarized in table 3.For strategy 5,with lattice QCDMYc,MNin the ΛcNCT potentials within the fitting regionEc.m.≤5 MeV,we presented the phase shifts of ΛcN3S1and3D1partial waves and inelasticity in figure 2.One can see that the ΛcN3S1and3D1phase shifts agree quantitatively with the lattice QCD data within uncertainties,and the asymptotic behaviors of inelasticity are in good agreement with the lattice QCD data.Comparing these results with those of strategy 6 whereMYc=MN,shown in figure 2,one can see that the ΛcN3D1interactions are attractive,contrary to the repulsive potential obtained in strategy 5.

In both cases,the extrapolation of the relativistic ΛcN3S1and3D1partial waves phase shifts and inelasticity to the physical point shows that the ΛcNinteraction is attractive in the3S1partial wave within the fitting region.Comparing the above results with strategy 1 (our previous study),where the ΛcN3S1potential is repulsive,we conclude that the extrapolated phase shifts of ΛcN3S1are not very stable.

To investigate whether the energy region fitted can affect the extrapolations,we also fitted the lattice QCD data up toEc.m.≤20 MeV in the covariant ChEFT approach.The results are shown in figure 3 in comparison with the results obtained by fitting only up toEc.m.≤5 MeV.The two fits are qualitatively consistent with each other.Only η1is closer to unity in the new fit.In addition,the extrapolated δ3S1and η1show some visible differences.Atmπ=138 MeV,δ3S1becomes smaller,and η1becomes more dependent on the cutoff.

4.2.2.Non-relativistic ChEFT.Focusing on the lattice QCD data withEc.m.≤5 MeV,we show in figure 4(the blue bands)the ΛcN3S1,3D1partial wave phase shifts and inelasticity obtained from strategy 7 in the non-relativistic ChEFT.The corresponding χ2/d.o.f.are listed in table 3.Here,we find that the non-relativistic phase shifts of ΛcN3S1partial wave and inelasticity are in qualitative agreement with the lattice QCD data in the region fitted.On the other hand,the ΛcN3D1phase shifts turn out to be positive,while the lattice QCD data are negative,though quite small.This is very different from the covariant case as shown in figure 3,where the3D1phase shifts are negative for the energy region studied.According to the previous experience in theNNsector [11,16],the two EFTs should behave similarly in the low-energy regime,while the covariant EFT usually agrees better with the lattice QCD data than the non-relativistic EFT in the relatively highenergy regime.The present results are in conflict with such expectations to some extent.A better understanding can only be achieved once more precise lattice data with realistic uncertainties become available.

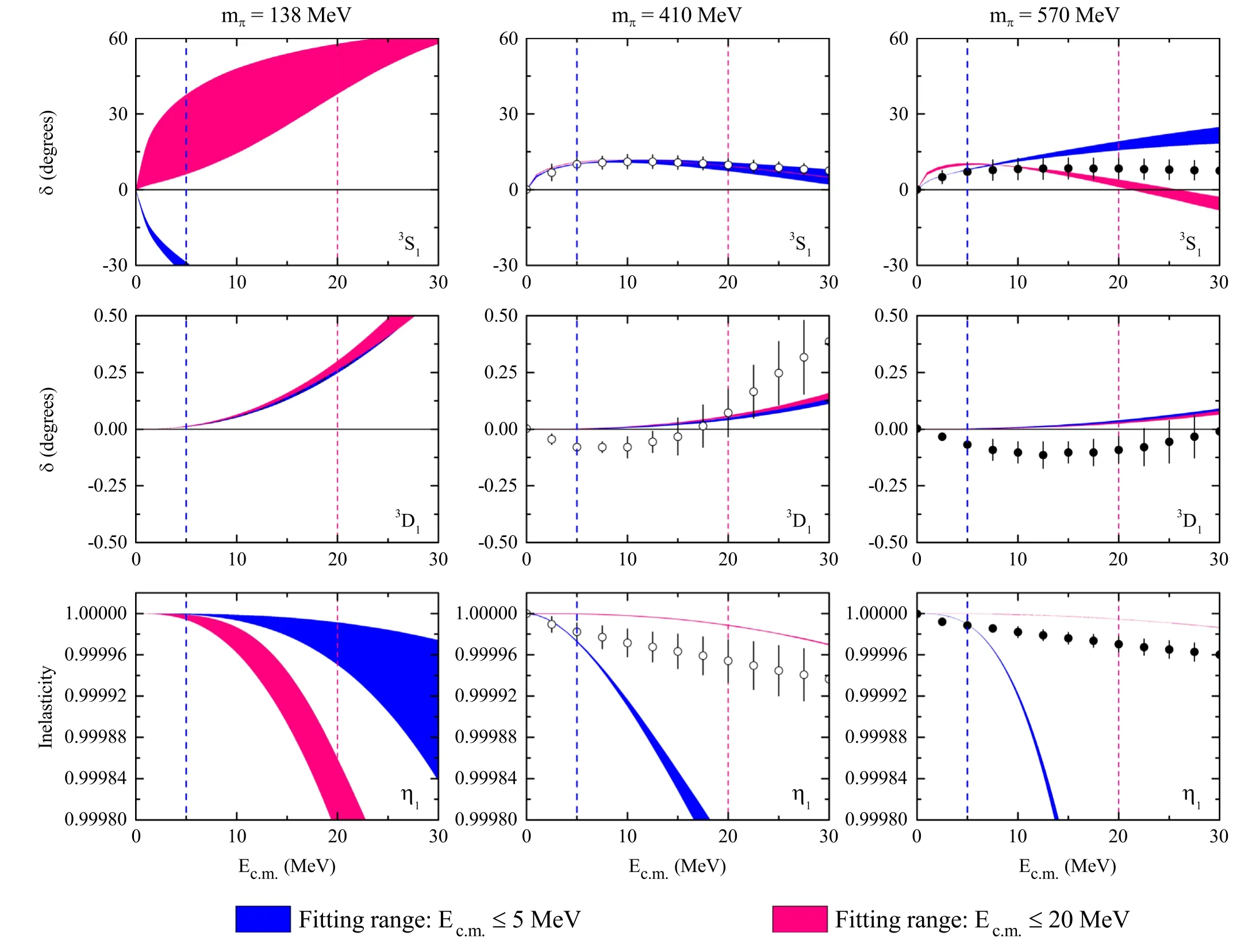
Figure 4.Same as figure 3,but for the non-relativistic ChEFT.

When we extrapolate the non-relativistic results to the physical point,we find that the ΛcNinteraction is repulsive in the3S1partial wave within the fitting region.Comparing these results with those of the covariant ChEFT and the left panel in Fig.4 of [2],we again conclude that the extrapolated ΛcN3S1interactions are not very stable,i.e.sensitive to the adopted fitting strategies.

The HB ΛcN3S1,3D1phase shifts and inelasticity with LECs obtained by fitting to the lattice QCD data up toEc.m.≤20 MeV (Fit 2) are compared to those obtained by fitting only up toEc.m.≤5 MeV(Fit 1)in figure 4.Compared to Fit 1,the descriptions of δ3D1remain almost unchanged in Fit 2,but the3S1phase shifts are very different.In Fit 1,δ3S1increases withEc.m.for the case ofmπ=570 MeV,while in Fit 2,it increases withEc.m.forEc.m.≤5 MeV and then decreases withEc.m.,which are in better agreement with the lattice QCD simulations at least for the energy region shown in this figure.Moreover,the difference for the case ofmπ=570 MeV eventually contributes to the completely different prediction of the physical δ3S1,where the phase shifts become positive in Fit 2.As for the case ofmπ=410 MeV,the two results show no qualitative difference.For the inelasticity,the results obtained in Fit 2 are closer to unity and larger than the lattice QCD simulations for the energy region fitted and become more independent onEc.m.as the pion mass increases.

5.Conclusion

The ΛcN3S1–3D1interactions were studied in leading order covariant ChEFT and next-to-leading order non-relativistic ChEFT.The low-energy constants were determined in two different strategies by fitting to the HAL QCD lattice data,i.e.(a)by only fitting to the ΛcN3S1partial wave phase shifts,(b)by a combined fit to the phase shifts of3S1,3D1and inelasticty η1.It was shown that for the first strategy,the predicted ΛcN3D1phase shifts from the covariant ChEFT were consistent with the low-energy lattice QCD data by using lattice QCDMYc,MNand retaining theSDcoupling in the contact potentials,while for the second strategy,one obtained results similar to those of the first strategy in the covariant ChEFT.However,the non-relativistic ChEFT predicts an attractive ΛcN3D1interaction in both cases,which is inconsistent with the low-energy lattice QCD data.In addition,we found that the extrapolated ΛcN3S1phase shifts in the physical region were very sensitive to the fitting strategies and the theoretical approaches used.The covariant ChEFT predicts a repulsive/attractive3S1interaction depending on the fitting strategy(a)/(b),while the non-relativistic ChEFT predicts the opposite,which also depends on the energy region fitted.These results indicate that more refined lattice QCD data are needed to reach a firm conclusion about the ΛcN3S1–3D1interactions.

It is necessary to point out that there are ongoing discussions on the validity of the HAL QCD method[34–36].In our present work,we have of course assumed that the method is valid and the3D1phase shifts and particularly the inelasticity are correctly extracted with the precision claimed in[18].Hopefully,the present study can motivate a closer look at the ΛcNinteraction in the3S1–3D1coupled channel.

Acknowledgments

This work was partly supported by the National Natural Science Foundation of China (NSFC) under Grants No.11 975 041,No.11735003,and No.11961141004.Yang Xiao acknowledges the support from China Scholarship Council.

ORCID iDs