Modification of laser-induced state in atomic attosecond transient absorption by the XUV pulse pair

Xuhong Li,Guanglu Yuan,Xiangyu Tang,Yong Fu,Kan Wang,Bincheng Wangand Cheng Jin,3,∗

1 Department of Applied Physics,Nanjing University of Science and Technology,Nanjing 210094,China

2 Experimental teaching center of physics,Nanjing University of Science and Technology,Nanjing 210094,China

3 MIIT Key Laboratory of Semiconductor Microstructure and Quantum Sensing,Nanjing University of Science and Technology,Nanjing 210094,China

Abstract Attosecond transient absorption (ATA) has been developed as an all-optical technique for probing electron dynamics in matter.Here we present a scheme that can modify the laserinduced state and the corresponding ATA spectrum via excitation by a pair of XUV attosecond pulses and by a time-delayed mid-infrared (MIR) laser probe.Different from the scheme of the electronic excitation by a single XUV attosecond pulse,the application of a pair of XUV pulses provides extra degrees of freedom,such as the time delay and the intensity ratio between two XUV pulses,which make it possible to adjust the pump process,resulting in the modification of the ATA spectrum.We show that by varying the time delay between the two XUV pulses,the population of the dark state and the ATA spectrum of the laser-induced state have periodic modulations.We also demonstrate that the peak of the ATA spectrum of the laser-induced state appears at a fixed time delay between the XUV pair and the MIR laser when the intensity ratio is large,and it changes with the time delay when the intensity ratio is small,which can be related to either one of two peaks in the population of the dark state.

Keywords: attosecond transient absorption,laser-induced state,XUV pulse pair,dark state,multilevel model

1.Introduction

Attosecond transient absorption (ATA) spectrum generated by an attosecond XUV pulse in the combination with a fewfemtosecond infrared(IR)pulse has been developed as an alloptical method widely applied for studying the interaction of laser fields with matter [1–12].ATA spectrum has been proven to be an excellent tool for probing the ultrafast subfemtosecond or attosecond electron dynamics not only in atoms [13–16],but also in molecules [17–22] and in solids[23–27].For atomic systems,the ATA spectrum displays several interesting features including the light-induced states[4,21],Autler–Townes splitting [28–30],hyperbolic sidebands associated with perturbed free induction decay [31],AC Stark shift [32],and so on,indicating various physical processes motivated by the electronic motion.

Like the common transient absorption techniques,ATA is a type of pump-probe spectroscopy.In the first ATA experiments performed in krypton [1,2],IR-driven strong-field ionization was used as a pump to generate electronic wave packets in the ions,which were then probed by attosecond XUV pulses.This scheme was used to explore the coherent hole dynamics in Kr+cations formed by infrared multiphoton ionization.In several recent experimental and theoretical works[16,22,28,33–35],an XUV attosecond pulse was used as a pump to generate a wave packet and then a moderately IR field(too weak to excite the atoms alone) was applied as the probe laser pulse.The resulting ATA spectrum was used for studying the Autler–Townes splitting of a laser-dressed atom and then an analytical formula was proposed to quantify the buildup time of the Autler–Townes splitting[28].Besides,the multilevel model has been used for investigating the transition dipole phase in the ATA spectrum of helium in a recent theoretical work [33].

At present,the most classical way to obtain the atomic ATA spectrum is: a single XUV attosecond pulse starts the clock by pumping the atomic system to some excited states,and then the dynamics of the system is changed by applying an IR laser field coupling to a nearby dark state.This timedependent modification interferes with the natural oscillations of atomic states,resulting in a richly characterized absorption spectrum.With the development (or the knowledge) of the attosecond laser technology,a pair of XUV attosecond pulses have been either generated in experiment [36] or proposed to be produced via spatiotemporal wavefront rotation induced by plasma in theory [37],which provides another degree of freedom to modify the process of electron motion.Such novel attosecond light source has been employed in the experiment.For example,Kollet al[36] validated the precision and the accuracy of the setup by XUV optical interferometry through the generation of a pair of XUV attosecond pulses and retrieved the energies of Rydberg states of helium in an XUV pump-probe photoelectron spectroscopy experiment.Recently,in a typical XUV+IR pump-probe experiment,they used two XUV attosecond pulses as pump pulses to dissociate and ionize hydrogen molecules to control the vibrational coherence ofcations and thus control the entanglement between photoelectrons and ions [38].However,according to the best of our knowledge,the XUV attosecond pulse pair have not been employed in the XUV+IR type experiments or theoretical studies for obtaining the ATA spectrum.

In this work,our main focus is to theoretically examine the modification of the laser-induced state in the atomic ATA by using two XUV attosecond pulses as pump pulses while a mid-infrared (MIR) laser is severed as a probe.This paper is structured as follows.In section 2,we will introduce theoretical methods for simulating the single-atom ATA spectrum.The multilevel model will be introduced to solve the timedependent Schrödinger equation (TDSE).In section 3,we will take the helium atom as a benchmark atomic system to discuss how an XUV pulse pair can manipulate the laserinduced state in the atomic ATA spectrum.This paper will be concluded in section 4.

2.Method

In this paper,both XUV pulses and the MIR laser are linearly polarized,the target atom is helium and the atomic unit is used.To obtain the atomic ATA spectrum under the XUV attosecond pulses combined with the MIR laser field at a specific time delay,we need to solve the TDSE of the electron.Taking the single-active electron approximation [39],the TDSE is expressed as follows:

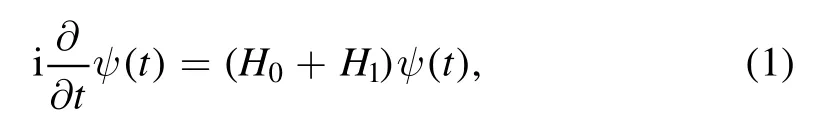
whereH0is the field-free Hamiltonian andH1=−zElaser(t)describes the interaction of the atom with XUV pulses and the time delayed MIR laser.This equation is within the dipole approximation and under the length gauge.Equation (1) can be approximately solved by truncating the basis set and including a few bound states only,which is called the multilevel model [31,40,41].In this model,the time-dependent wave function of the electron can be expanded by the eigenstates of the undressed atomic system as:

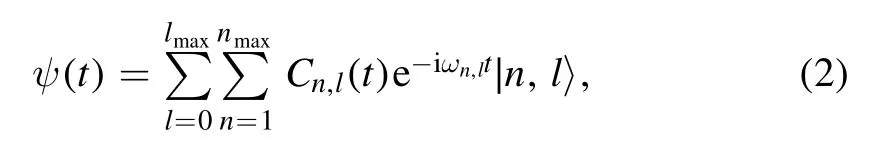
wherenmaxandlmaxare the largest principal and angular momentum quantum numbers of atomic states.The Dirac symbol|n,l〉represents the eigenstate,and theCn,l(t)and ωn,lare the time-dependent coefficient and the eigenenergy of the electronic state,respectively.

Substituting equation (2) into equation (1),one can get the equation:

where the subscriptsiandjrepresent the two states with different quantum numbers (n,l) and μi,jis the transition dipole moment.And the laser-induced dipole momentd(t) is obtained by

Here c.c.means the complex conjugate.To make the induced dipole momentd(t)smoothly go to zero when the laser pulse is off,it is multiplied by a window function in the form of,in whichT2is called the dephasing time.

The single-atom response function is given directly (see[31,40] for details) as follows:

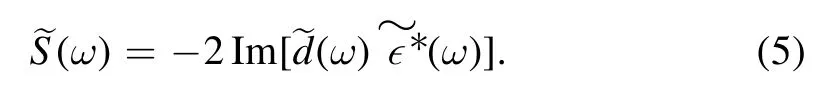
Here(ω)is the Fourier transform of the time-dependent induced dipole moment and(ω)is the Fourier transform of the combined electric field.By using equation (5),we can calculate the attosecond absorption spectra at a specific time delay between the XUV pulses and the MIR laser.Figure 1 shows the comparison of two schemes for generating the ATA spectrum.Figure 1(a) is a schematic plot of the typical ATA process involving three states.At first,the pump XUV pulse is applied to the He atom and excites the electron transition from the ground state 1s to the bright state 2p.Then,the probe MIR pulse interacts with this system and couples the bright state 2p to the nearby dark state 2s.Finally,the electron absorbs the energy of the probe MIR photon ω and makes a transition to the laser-induced state 2s+ω.We focus on the ATA spectrum around the laser-induced state 2s+ω.Different from the typical ATA process,in our scheme,an XUV pulse pair is used as the pump pulse,as shown in figure 1(b).We can adjust the time delay and the intensity ratio between the two XUV pulses,and with the time-delayed MIR laser pulse,it can modulate the excitation process from 1s to 2p and the population of the dark state 2s.As the dark state 2s is closely related to the laser-induced state 2s+ω,the ATA spectrum around 2s+ω can thus be modified in figure 1(b).The different features of the ATA spectrum between the typical ATA scheme and our scheme can be clearly observed in figures 1(a) and (b).Besides,to clearly show the relationship between the bound states and the laser-induced states of Helium,we display the sketch of the energy levels of Helium in figure 1(c).It is shown that 2s and 2p have adjacent energies with the laser-induced states 2s+ω and 2s −ω,thus the electron can easily make transitions from 2s and 2p to 2s+ω and 2s −ω.

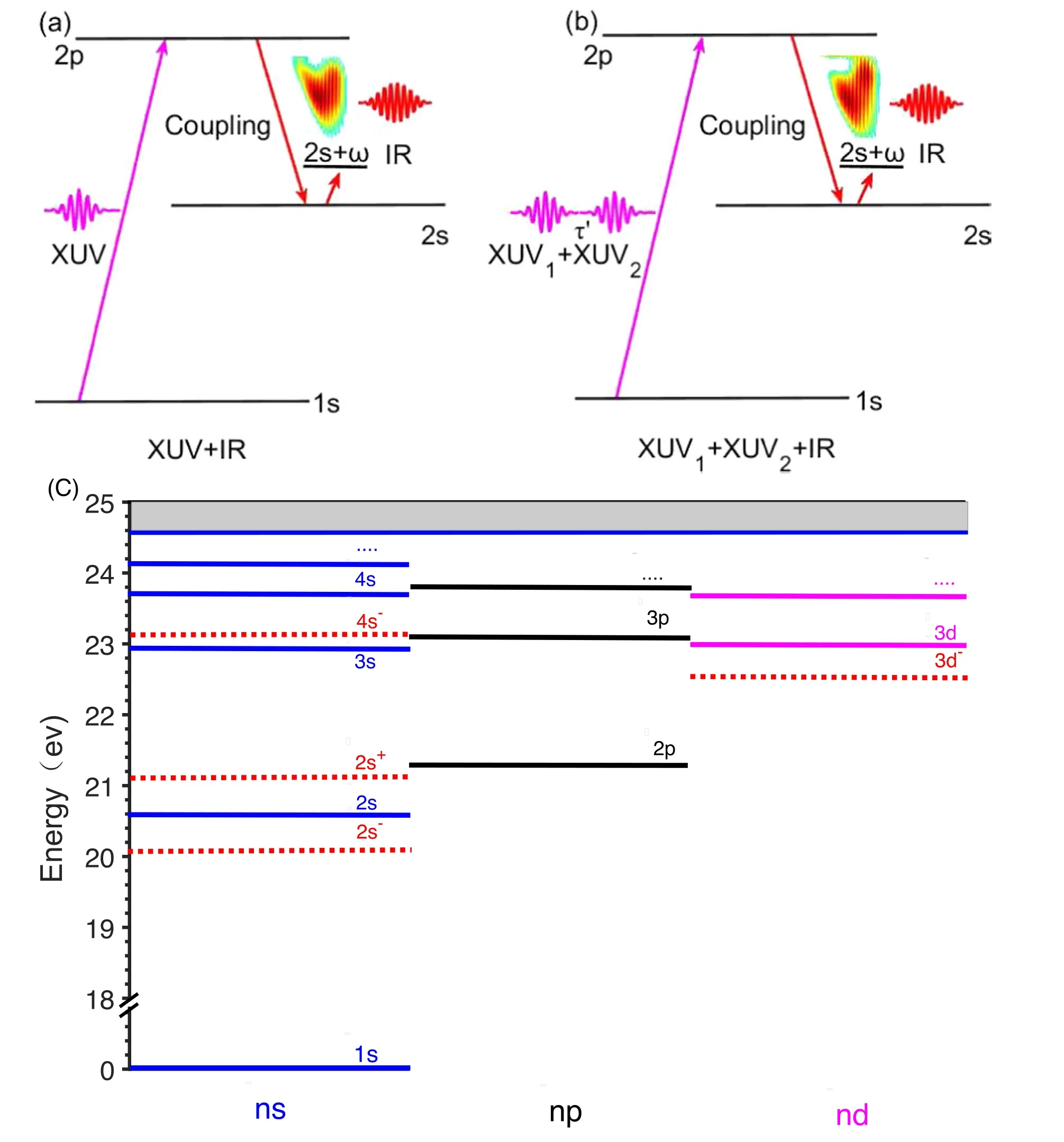
Figure 1.(a)and(b):schematic diagram of obtaining the ATA spectra of helium under two different schemes.The ATA spectrum around the laser-induced state is obtained by applying an IR laser (red) with the time-delayed attosecond pulse (pink) in (a) or attosecond pulse pair(pink)in(b)into a three-level atomic system.The time delay of the two XUV pulses in(b)is represented by τ′.(c)The sketch of the energy levels of Helium.The dashed line represents the laser-induced states.

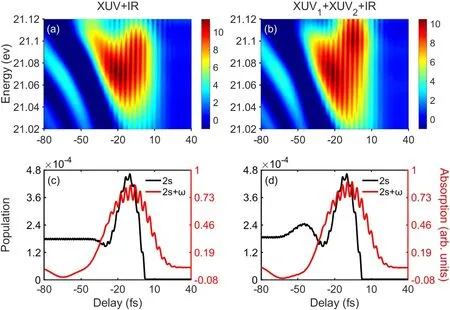
Figure 2.The ATA spectra of He were calculated at two different schemes:(a)MIR and single XUV and(b)MIR and XUV pulse pair.The time delay of the two XUV pulses is τ′=−3.9 cycles(1 cycle ≈8 fs).The red lines in(c)and(d)are the integrated ATA spectrum around the photon energies of the laser-induced state in(a)and(b).The black lines in(c)and(d)are the maximum 2s population as a function of the time delay between the MIR laser and the XUV pulse (or the XUV pulse pair).Note that the red lines in the (c) and (d) are normalized.

3.Results and discussion

In this section,we will first compare the ATA spectra by using a single XUV pulse and a XUV pulse pair as the pump,and then discuss the relationship between the ATA spectrum of the laser-induced state 2s+ω and the electron population of the dark state 2s.Following that,we will reveal how the XUV pulse pair manipulates the dark state and the corresponding ATA spectrum of the laser-induced state,and we will also study the dependence of the ATA spectrum of the laserinduced state on the time delay and intensity ratio between the two pump XUV pulses.

In the calculations,the energy of the ground state 1s is taken as −24.59 eV,and the initial electron population is 1 for the ground state and 0 for other excited states.The laser parameters used are as follows: the wavelength of the MIR pulse is 2400 nm,its full-width-at-half-maximum (FWHM)duration is 32 fs,its peak intensity is 1×1011W cm−2,and its envelope is cosine squared.The weak intensity is used to avoid the nonlinear effect induced by the MIR electric field.The XUV pulses are assumed to have a Gaussian profile with the FWHM duration of 400 as,centered at the photon energy of 22 eV.The peak intensity of the XUV1pulse is 6×109W cm−2,and it is 6×107W cm−2for the XUV2pulse.Figure 2(a) shows the typical ATA spectrum driven by the single XUV and MIR pulses in the different time delay between them.Note that the spectrum is only shown around the laser-induced state (2s+ω) in a narrow spectral region(0.1 eV) of photon energy.It is found that the main ATA occurs around the time delay of −50 fs to 10 fs.The negative time delay means that the XUV pulse arrives before the center of the MIR pulse.With the variation of the time delay,the ATA spectrum has periodic oscillation and the peak of the ATA spectrum appears at the time delay of −20 fs while the photon energy is 21.07 eV.In figure 2(b),we plot the ATA spectrum generated from the XUV pulse pair and the MIR laser pulse.Comparing with figure 2(a),we can see that the main structures of the ATA spectrum are maintained,i.e.the periodic oscillation in the ATA spectrum remains and one of the peaks in the ATA spectrum appears at the time delay of−10 fs.There also exists a difference.When the time delay is about 5 fs,another obvious peak in the ATA spectrum appears at the photon energy of 21.10 eV driven by the XUV pulse pair.These results show that the extra XUV pulse can change the ATA spectrum in some way.In figures 2(c) and(d),we give the population of the dark state 2s when the laser electric field is maximum and also show the integrated ATA spectrum around the laser-induced state 2s+ω.It is noted that the integrated ATA spectrum around the laser-induced state 2s+ω is the result of the integration from figures 2(a)and(b)around the energy range of 21.02 and 21.12 eV.From figures 2(c) and (d),we can see that the peak position of the maximum 2s population generally matches well with the integrated ATA spectrum around 2s+ω for both the single XUV and the XUV pulse pair as the pump pulse.It is because the laser-induced state 2s+ω results from one MIR photon absorption of the dark state 2s.Thus it is expected to see a good correspondence between the population of the dark state and the ATA spectrum of the laser-induced state.However,there still are some differences.In figure 2(c),only one peak appears in the maximum 2s population when the time delay is−10 fs.On the contrary,in figure 2(d),there are two peaks:the first peak appears at the time delay of −45 fs and the second peak appears at the time delay of −10 fs,which is inconsistent with the integrated ATA spectrum.In the following,we will explain the origin of these two peaks and discuss how to modify the ATA spectrum of the laser-induced state by using the XUV pulse pair.

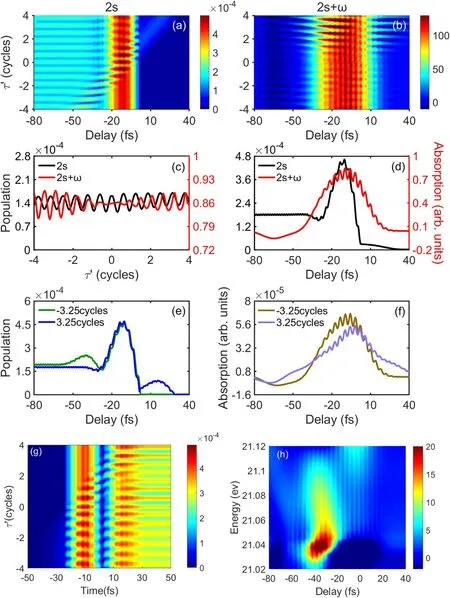
Figure 3.The population of the dark state 2s(a)and integrated ATA spectrum around the laser-induced state 2s+ω(b)as a function of the time delay τ′ of the XUV pulse pair and the time delay between the XUV1 pulse and the MIR laser.(c) The average of the 2s population(black)in(a)and the averaged ATA spectrum in(b)(red)over the time delay between the XUV1 pulse and the MIR laser as a function of τ′.(d) The average of the 2s population (black) in (a) and the average ATA spectrum in (b) (red) over the time delay of the XUV pair as a function of the time delay between the XUV1 pulse and the MIR laser.The population of 2s state(e)and the integrated ATA spectrum(f)as a function of the time delay when τ′=−3.25 cycles(green)and 3.25 cycles(blue).Note that the red lines in the(c)and(d)are normalized and the intensity ratio of the XUV pair is fixed at 100:1.(g)The population of the dark state 2s as a function of the time delay τ′of the XUV pulse pair and the time of the laser electric field when the intensity ratio between two XUV pulses is 100:1 and the time delay between XUV1 and IR is −20 fs.(h) The ATA spectrum when τ′=−4 cycles,the intensity ratio and the time delay are the same with (g).

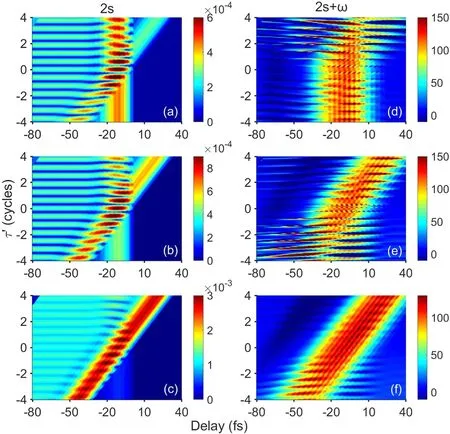
Figure 4.(a)–(c): the 2s population as a function of the time delay between the XUV1 pulse and the MIR pulse and τ′ calculated with the three different intensity ratios of the XUV pulse pair (10:1,2:1 and 1:10),respectively.(d)–(f): the integrated ATA spectrum around the 2s+ω state with the intensity ratios the same as those in (a)–(c).

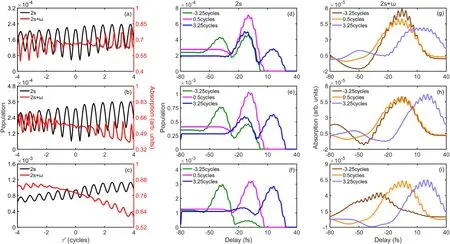
Figure 5.(a)–(c):the average of the 2s population(black)and the averaged ATA spectrum(red)as a function of τ′.The population of 2s state(d)–(f) and the integrated ATA spectrum (g)–(i) as a function of the time delay between the XUV1 pulse and MIR laser when τ′=−3.25 cycles,0.5 cycles,and 3.25 cycles.The intensity ratio of the XUV pulse pair is 10:1,2:1,and 1:10 for first row,second row,and third row,respectively.

In figure 3,we change the time delay between the two XUV pulses and show the 2s population and the integrated ATA spectrum around the state of 2s+ω as a function of the time delay between the XUV1pulse and the MIR laser in figures 3(a) and (b),respectively.To distinguish the time delay between the two XUV pulses in a pair and the time delay between the XUV1pulse and IR laser,the former is defined asτ′.In figure 3(a),one can find that similar to the results in figure 2(d),the population of 2s state also has a twopeak structure.One of the peaks is about fixed around the time delay of −10 fs while the position of the other peak changes withτ′.Whenτ′ is increased from −4 to 4 cycles,the position of the second peak is changed from −50 to 30 fs.In detail,whenτ′ is −4 cycles (−32 fs),the position of the second peak is around −50 fs and the distance between the two peaks is about 30 fs.Whenτ′is 0 cycle,the second peak position is changed to around −10 fs and the two peaks almost coincide.Ifτ′is 4 cycles(32 fs),the distance between the two peaks is also about 30 fs.The close relation between the distance of two peaks and the time delayτ′ of two XUV pulses shows that the second peak in the 2s population is generated due to the presence of the second XUV pulse(XUV2).In other words,the addition of the XUV2pulse is able to change the electron excitation process,thus one can expect to modify the laser-induced state in the ATA spectrum by using the XUV2.A general modification of the integrated ATA spectrum around the 2s+ω state can be seen in figure 3(b).In figure 3(c),we compare the averaged results of the 2s population and the ATA spectrum as a function ofτ′.Note that the averaged 2s population and the ATA spectrum are the average results over different time delay between XUV1and MIR pulses in figures 3(a) and (b).Both the 2s population and the ATA spectrum have periodic oscillation whenτ′ is increased from −4 to 4 cycles.The average modulation period of the 2s population is 0.65 cycles,and for the ATA spectrum,it is 0.55 cycles.Therefore,the change ofτ′ can modifies the population of 2s state and the ATA spectrum effectively.Besides,whenτ′ is around 0,the difference between the 2s population and the ATA spectrum is maximum.Whenτ′ is larger than 2 cycles,the 2s population agrees well with the ATA spectrum.In figure 3(d),we calculate the average of the 2s population (black) in figure 3(a)and the ATA spectrum in figure 3(b)(red)as a function of the time delay between the XUV1pulse and the MIR laser.The average results here mean the average results over differentτ′between two XUV pulses in figures 3(a)and(b).We can see that they both have one peak only and their peak positions appear at the same time delay.In figures 3(e) and (f),we display the population of 2s and the integrated ATA spectrum whenτ′ is −3.25 cycles and 3.25 cycles,respectively.However,they do not match well.There are two peaks in the 2s population and only one peak in the ATA spectrum.In figure 3(g),we display the 2s population as a function of the time delayτ′between two XUV pulses and the time covering the overlap of IR laser and XUV pulses.The intensity ratio between two XUV pulses is 100:1 and the time delay between XUV1 and IR pulse is −20 fs.We can find that with the variation ofτ′,the 2s population induced by the XUV pulse pair has a periodic oscillation which is obvious whenτ′<0 and inconspicuous whenτ′>0.The periodic oscillation results from the interference between the 2s populations induced by two XUV pulses.Whenτ′=4 cycles,the XUV2appears at about 12 fs,therefore the interference effect only appears after 12 fs.Before 12 fs,the 2s population only generates by the XUV1.Whenτ′=−4 cycles,the XUV2appears at about −52 fs,therefore the interference effect is always present from −52 fs to 30 fs.Figure 3(h) shows the ATA spectrum whenτ′=−4 cycles,comparing with the ATA spectrum in figure 2(b),it is seen that the interference effect will affect the final ATA spectrum and generate destructive interference in the ATA spectrum.

To reveal the difference between the population of 2s and the ATA spectrum of 2s+ω whenτ′ is between −3.25 or 3.25 cycles,we further change the intensity ratio between the XUV pulse pair.In figure 3,the intensity ratio between XUV1and XUV2pulses is fixed at 100:1.In figure 4,it is changed from 10:1 to 1:10 while the intensity of XUV1pulse is fixed at 6×109W cm−2.Comparing with figure 3(a) and figure 4(a),we can find that with the decrease of intensity ratio from 100:1 to 10:1,the peak in the 2s population induced by the XUV2pulse becomes stronger and thus the strengths of two peaks are comparable.With the intensity ratio further decreased,the peak generated from the XUV2pulse becomes stronger and stronger in figures 4(b) and (c),and it is even stronger than the fixed peak in figure 4(c).For the integrated ATA spectrum of 2s+ω,one can also see that with the decrease of the intensity ratio,the influence of the XUV2pulse becomes more obvious and the dependence of the ATA spectrum on the time delay is dramatically changed.When the intensity ratio is large,the peak in the ATA spectrum is fixed at around −10 fs,see figure 3(b).While the intensity ratio is decreased,the peak shifts in the time delay as the change ofτ′,see figures 4(d)–(f).

Furthermore,we show the average of the 2s population(black)and the average of the integrated ATA spectrum(red)as a function ofτ′ in figures 5(a)–(c) for three different intensity ratios,respectively.Note that the average of the 2s population and the integrated ATA spectrum are the average results over different time delay between XUV1and MIR pulses in figure 4.For the big intensity ratio (10:1),the modulation periods of the 2s population and the ATA spectrum match well,see figure 5(a).The difference between the 2s population and the ATA spectrum becomes large when the intensity ratio is decreased.When the intensity ratio is 1:10,their difference is maximum.It means that to obtain a better modulation result,the intensity ratio between the XUV pulse pair should not be too small.In figures 5(d)–(f),the 2s population as a function of the time delay is shown for some selectedτ′.Whenτ′ is −3.25 cycles (green),there are two peaks and the first one occurs around −40 fs and the second peak appears at the time delay of −10 fs.Whenτ′ is 0.5 cycles (pink),there only has one peak at −10 fs.Whenτ′ is 3.25 cycles (blue),there also has two peaks and the first one occurs around the −10 fs and the second peak appears at the time delay of 20 fs.These behaviors are very similar for different intensity ratios.In figures 5(g)–(i),we show the integrated ATA spectrum as a function of the time delay for some selectedτ′.Whenτ′ is −3.25 cycles,the peak appears at about −10 fs.When the intensity ratio is smaller,see figures 5(h) and (i),it shifts to the negative time delay and when the intensity ratio has the smallest value,see figure 5(i),it shifts to about −40 fs.One can easily find the corresponding peaks in the 2s populations in figures 5(d)–(f).A similar correspondence between the peak in the 2s population and the peak in the integrated ATA spectrum can also be identified whenτ′ is 0.5 cycles or 3.25 cycles.These results again show the close relationship between the 2s population and the ATA spectrum of 2s+ω.With the decrease of the intensity ratio,the influence of the XUV1pulse is gradually decreased while the effect of the XUV2pulse is increased.The modification of the 2s population due to the interference effect between two XUV pulses is finally reflected in the ATA spectrum of 2s+ω.

4.Conclusion

In summary,we proposed to adjust the laser-induced state in the ATA by using an XUV pair in the pump process while a MIR laser is employed in the probe step.We identified that the ATA spectrum of the laser-induced state 2s+ω is closely related to the population of the dark state 2s.Thus the modification of the ATA spectrum by varying the time delay and the intensity ratio between the two XUV pulses can be well understood by investigating the population of the 2s state.We found that by changing the time delayτ′ between the XUV pulse pair,both the population of the 2s state and the corresponding ATA spectrum change periodically with a period of 0.5 laser cycles.Moreover,we showed that when the intensity ratio of the XUV pulse pair is larger than 10:1,there is only one peak in the ATA spectrum occurring at a fixed time delay between the XUV pair and the MIR laser,and with the decrease of the intensity ratio,the peak in the ATA spectrum is linearly shifted with the time delay.Such behaviors can be understood by the populations of the 2s state obtained at different intensity ratios of the XUV pulse pair.It shows that the population of the 2s state has a double peak structure.One is fixed at a time delay and the other is changed with the time delay.With the decrease of the intensity ratio,the second peak in the 2s population becomes more obvious because the intensity of XUV2pulse is gradually increased.Our study provides a new scheme to control the electron dynamics with a XUV pulse pair,which can be decoded from the ATA spectrum of the laser-induced state.

Acknowledgments

This work is supported by the National Natural Science Foundation of China(Grant Nos.91950102 and 11834004),the Natural Science Foundation of Jiangsu Province (Grant No.BK20220925) and the Funding of Nanjing University of Science and Technology (NJUST) (Grant No.TSXK2022D005).

ORCID iDs