Can sub-GeV dark matter coherently scatter on the electrons in the atom?
2023-02-16JiHengGuoYuXuanSunWenyuWangandKeYunWu
Ji-Heng Guo,Yu-Xuan Sun,Wenyu Wangand Ke-Yun Wu
Faculty of Science,Beijing University of Technology,Beijing,China
Abstract A novel detection of sub-GeV dark matter is proposed in the paper.The electron cloud is boosted by the dark matter and emits an electron when it is dragged back by the heavy nucleus,namely the coherent scattering of the electron cloud of the atom.The survey in the x-ray diffraction shows that the atomic form factors are much more complex than the naive consideration.The results of the relativistic Hartree–Fock (RHF) method give non-trivial shapes of the atoms.The detailed calculation of the recoil of the electron cloud,the kinetics,the fiducial cross section and the corresponding calculation of detection rate are given analytically.The numerical results show that the limits of the RHF form factors are much more stringent than the recoil of a single electron,almost 4 orders stronger,and also give tight limitations compared to the Migdal effect below about several hundred MeV.The physical picture and the corresponding results are promising and need further exploration.
Keywords: dark matter,coherent scattering,form factor
1.Introduction
Observations in cosmology and astrophysics clearly support the presence of dark matter(DM)[1].Its features,such as mass and interactions are however still unknown.One of the most promising experimental avenues is to search for small energy depositions from the dark matter elastically scattering in sensitive detectors on Earth.An attractive dark matter candidate is weakly interacting massive particles(WIMPs),which have been explored in various direct detection,indirect detection and collider experiments.The null results have produced very stringent limits on the WIMP-nucleus scattering cross section heavier than 1 GeV.Thus the hunt for sub-GeV dark matter is a hot topic at the cutting edge of physics research.Nevertheless,the sub-GeV dark matter can emerge in some fundamental theories such as the next-to-minimal supersymmetry standard model [2–4].The self-interaction can be realized between the light dark matter to solve small structure problems etc [5].However,as the sensitivity is lost for light dark matter detection,the traditional strategies for detecting WIMP-type dark matter are no longer feasible.Physicists are striving to create techniques for detecting light dark matter.
Among all the new ways of searching for sub-GeV dark matter,the ionization signal on the detectors could be the most promising one.In the dual-phase xenon time projection chamber,the xenon atoms in the liquid xenon phase can be ionized due to a collision.Then the ionized electrons drift into the gaseous xenon layer at the top of the detector in presence of an external electric field,which produces a proportional scintillation light,namely the S2 signal.In the theoretical studies,such ionization signals can come from the DM-electron scattering[6–17] or the DM-nucleus scattering through the Migdal effect that originates from the non-instantaneous movement of electron cloud during a nuclear recoil event [18–35].
In addition to those DM-electron scattering and the Migdal effect on ionization detection,there is another way that seems to be promising in the search for light dark matter.It is well known that the electrons which are bounded by the nucleus in an atom form the electron cloud.If the dark matter can collide with a single electron in the atom,it can also collide with the whole cloud of the atom too.In fact,this is just the coherent scattering in dark matter detection.For example,there can beZ2(charge number) orA2(atom number) enhancements in the spin-independent detection of the DM-nucleus scattering.As for the detection of ionization,the question is that does similar coherent enhancement exist in the recoils of the electron.This is not a trivial question since it can be seen in the x-ray diffraction (XRD) on the atom,there do have the coherent scattering of electron cloud from which the atom scattering form factor can be derived.As for the sub-GeV dark matter,the de Broglie wavelength of the dark matter can be sufficiently small to inject into the target atom,the same as the diffraction of the incident x-ray too.The collision can boost the electron cloud to a sizable velocity.After that,it can also be dragged back by the static heavy nucleus and throw away an electron to give a similar ionization S2 signal.Such a mechanism seems reasonable,or at least it should be checked whether this effect can exist or can be significant for the detection.
In this paper,we will check this novel detection of scattering on the electron cloud to see whether a coherent enhancement exists in the recoils of the electron.As the process is similar to the diffraction of x-ray scattering on the atom,we will show our understanding of the coherent scattering from the point of the XRD at first.Then we will show how to calculate the coherent scattering between dark matter and the electron cloud.After that,the constraints from the current dark matter detection are calculated numerically for comparison with the results of the DM-electron scattering and the Migdal effect.The paper is organized in the following:the coherent scattering of the electron in an atom is discussed in section 2;the calculation methodology for the coherent scattering is given in section 3;the numerical results and the comparison with the other strategies are shown in section 4,and our conclusion is given in section 5.
2.Coherent scattering of the electron in an atom
Figure 1 shows the scattering processes of the electrons when the dark matter collides on the atom in which figure 1(a)shows a sketch map of that the dark matter scattering on a single electron and figure 1(b) shows the sketch map of the Migdal effect.A detailed calculation of the first two processes and the comparison between them can be found in[26].Here we just list the essential points of these two processes:

Figure 1.The three processes which can induce ionization: the collision between dark matter and single electron,the Migdal effect and the collision between dark matter and the electron cloud of an atom,respectively.
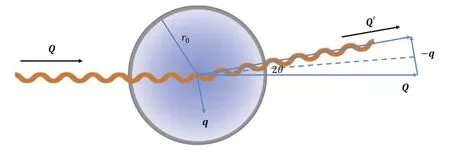
Figure 2.The x-ray diffraction on the atom.
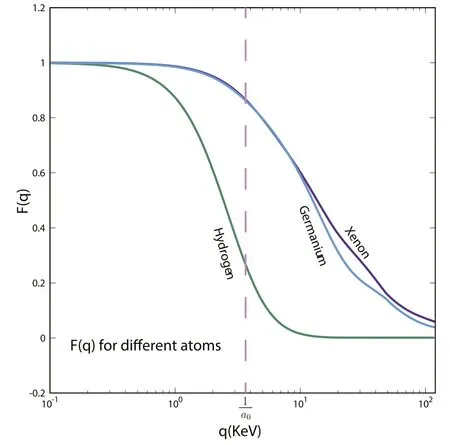
Figure 3.The atomic form factor of hydrogen,germanium and xenon in which the hydrogen’s is calculated analytically from the Schrödinger equation,and the other two are calculated by Relativistic Hartree–Fock method.The corresponding momentum of the inverse Bohr radius 1/a0 is shown as the dashed vertical line.All the form factors are normalized to 1 at zero momentum transfer q=0 for the comparison.
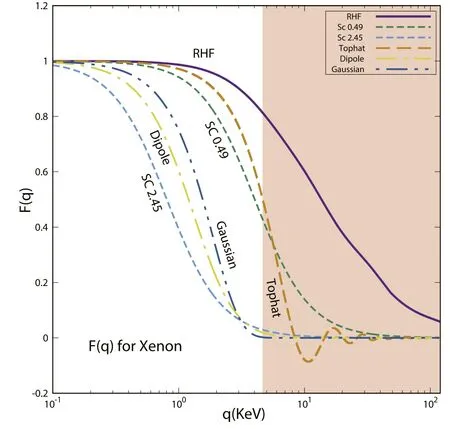
Figure 4.Xenon’s F(q) gets from the RHF method (purple line),screened Coulomb potential with two different radii (green/blue short dash)and the Tophat(orange dash),Dipole (yellow dot dash),Gaussian (blue double dots dash) shapes.The incarnadine shade is the interval of momentum transfer q in the detection of light dark matter.The form factors are normalized to 1 at zero momentum transfer q=0 for the comparison.
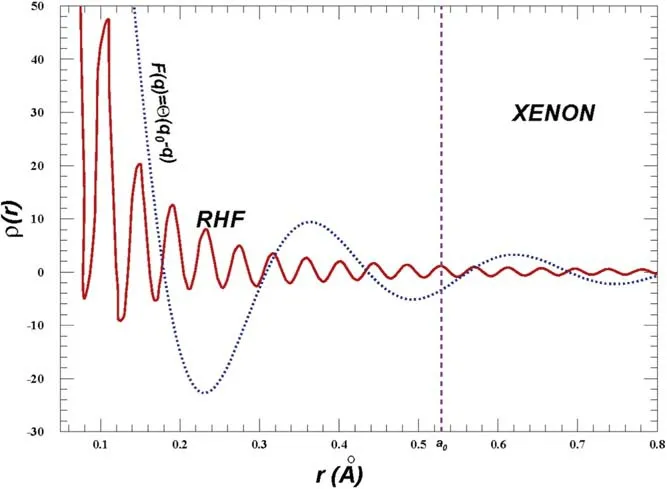
Figure 5.Charge distribution of ρ(r) of Xenon,calculated by the Fourier transformation of RHF f(q) (red solid line) and a ‘Tophat’model(blue dot line)in momentum space that F(q)=θ(q0-q)with q0=25 KeV.The dashed line shows the position of the Bohr radius.
1.In the recoil of the electron,the dark matter transfers momentumqdirectly to the single electron bounded in the atom,giving the ionization electron with recoil energyEeand momentumke.The impulse approximation[36] can be adopted in the theoretical calculation of the rate.
2.For the Migdal effect,the dark matter transfer momentumqto the nucleus.The momentum transfer happens much faster than the light-crossing time of the electron cloud,thus the nucleus gets a sudden‘movement’with velocityvAwhich can drag the electron cloud to the same velocity and throw away an electron with energyEeand momentumke.The inner product of the containing phase between the eigenstate wave function at rest and the Galilean transformation of the energy eigenstates of the moving atom gives the amplitude of the throwing rate of the electron.
3.The numerical results show that the Migdal effect is always subdominant to the electron scattering when the mediator is light.But it can dominate the ionization for heavy mediator and mass of the dark matter in hundreds of MeV range.
In addition to these two processes,we propose another novel collision between the dark matter and the electron cloud which is formed by the bounded electrons in an atom.The corresponding sketch map of the process is shown in figure 1(c).The electron cloud is taken as a ‘ball’ composed of the distributed electric charge,of which the amount is the charge number of the corresponding target element.As the mass of the dark matter is at the MeV order,one can simply figure out the de Broglie wavelength of the dark matter is much smaller than the radius of the target atom which is at the order of Bohr radius.Thus the collision between dark matter and the electron cloud can be considered as a collision between a ‘point’ and a ‘puffy ball’ [37,38].The corresponding scattering rate is always conveniently calculated in the momentum space,and the Fourier transformation of the charge distribution ρ(r) gives the form factorF(q) to account for the coherence of the charge distribution.The whole picture is similar to the diffraction of x-ray scattering on the crystal,thus before going to further explore the detection of dark matter,we discuss some essentials of XRD.
2.1.Atomic form factor in XRD
The XRD is a powerful tool widely used in research and the industry.While XRD is usually well known for qualitative and quantitative analyses of crystalline phases in materials,far more information can be obtained from a careful analysis of the diffraction patterns or by using specific XRD settings:i.e.characterization of solid solutions,crystallite size and shape,crystal orientation,etc.In XRD analyses,the diffraction of a wave of the characteristic length λ is required to be of the same size as the interatomic separation of the crystal.However,XRD can also detect the inter-structure of a specific atom which is called the small-angle technique.The sketch map is shown in figure 2.Such a small-angle technique,which is also known as the forward scattering in the scattering theory [39],is a method of investigation of non-periodic systems.The physics principles of the scattering are the same for both wide-angle diffraction and small-angle diffraction,in which the angle-dependent scattering amplitude is related to the electron-density distribution of the scattering by a Fourier transformation.The main difference between wide-and small-angle diffraction in XRD is that we have a periodic arrangement of identical scattering centers(particles)in wideangle diffraction,while the scattering center is limited in size,non-oriented,and non-periodic,but the number of the particles is high and this can be assumed to be identical of the small-angle diffraction.Thus small-angle diffraction can give a detailed investigation of a single target.There are both coherent and incoherent scattering in the XRD.For scattering on a single electron,they are called Rayleigh scattering and Compton scattering,respectively.As shown in figure 2,the momentum transferqto the electron can be easily derived from the small-angle deviation from the incident x-ray,thus the parameter sinis always adopted for the description of the form factor in the momentum space with the relation

The summation of all the electrons gives the atomic scattering form factor

For the scattering by the atomic electrons,the phase of coherent scattering is by convention related to that of the free electron at the nucleus.There is a phase shift of π for scattering from a free electron.And the coherent scattering in the XRD is [40]

In the above equation,Ieis the intensity of the scattering per unit solid angle,it is calculated from the Thomson formula

in whichI0is the intensity of the unpolarized incident beam andreis the classical radius of the electron(2.818×10-15m).Note thatIeandI0have different dimensions.Another issue that should be mentioned is that the momentum of the incident x-rayQis much greater than the momentum transferq.This means that the wavelength of the incident x-ray is much smaller than the inverse momentum transfer,λX≪1/q.Thus above calculations are reliable when the wavelength of the x-ray is larger than the classical radius of the electron,no matter how large the atom is.This is the key point of the understanding of the XRD which can be simply applied to the scattering of dark matter.The details are discussed in the next section.
It is usually considered common sense that the atomic form factorF(q)could be described by a function that equals the charge numberZat zero momentum transfer and roughly decreases with the multiplicative inverse of the atom radius quickly.However,things are contrary to the usual expectation.For the Hydrogen atom,F(q) can be got analytically by solving the Schrödinger equation,it is effectively zero for sin>1.5Å-1.Those for heavier atoms are for relativistic wavefunctions which can be calculated by the Relativistic Hartree–Fock (RHF) method of which the details can be found in Refs.[41,42]and all the results are summarized and listed in [40].Note that the RHF form factor is used for searching for Axion dark matter in inverse Primakoff scattering[43]and in[44]trying to find observing atomic effects in coherent neutrino scattering.Usually,the form factor can be effectively described by ‘Gaussian’ fits in the range 0Å-1<(s inθ)/ λ<2.0Å-1

Take the xenon atom as an example,the fit parameters in the above equation area1=20.2933,b1=3.9282;a2=19.0298,b2=0.344;a3=8.9767,b3=26.4659;a4=1.99,b4=64.2658;c=3.7118.But as the angle increases to 2.0Å-1<(s inθ)λ<6.0Å-1,[45] shows that the fitting formula above is highly inaccurate,as the scattering angle increasing,and they produced a ‘logarithmic polynomial’curve-fitting routine based on the equation for these high angles.Again,take the xenon atom as an example,thecivalues arec0=4.24610,c1=-1.56330,c2=3.04200,c3=-2.34290 give a close fit to the atomic scattering factor curves over the range and the correlation coefficient is 0.999.

In order to show the differences,we show the form factorF(q)for hydrogen,germanium and xenon atoms in figure 3,in which the hydrogen form factor is calculated analytically from the Schrödinger equation,and the other two are calculated by RHF.The corresponding momentum of inverse Bohr radius 1/a0is shown in the dashed vertical line in the panel.Note that all the form factors are normalized to 1 at zero momentum transferq=0 for the comparison.The form factor of hydrogen is a ‘Dipole’ form,and it decreases with the momentum transferqoutside 1/a0very quickly.As for the germanium (125 pm) [46] and xenon (108 pm) of which the radii are at the order of Bohr radius,contrary to common sense,theF(q) does not decrease at the border of inverse radius.They can maintain a sufficiently large value to the much largerq≫1/a0.This is a very important point of this work,the largeF(q) at the large momentum transfer can significantly enhance the rate of the recoils of the electron cloud.Before going into detail,we will show another atomic form factor in the literature.
2.2.Other atomic form factors
In addition to RHF atomic form factor in XRD,there are several other form factors applied in different physical circumstances.The first one is the screened Coulomb form factor which is usually used for the detection of Axion dark matter[43].This form factor is defined for the atom of which the positive charge of the nucleus in the atom center is screened by the electron cloud [47–49],forming a Yukawa potential
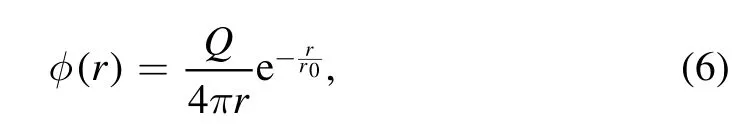
whereQis the atomic charge,r0is the screening length.In fact,equation (6) is the electrostatic potential of the atom.Using Poisson’s equation ∇2φ=-ρ,we can get the charge density distributions outside the nucleus.Note that the potential(6)is formed by the positive charge of the nucleus in the atom center (δ(r) function density) and the negative charge of the electrons outside.Thus remove the delta function charge distribution and do the Fourier transformation,we can obtain electron density distribution in the momentum space,namely the form factor

For the xenon atom,there are two results of the screening length used in the literature:r0=0.49 Å is calculated in[50],r0=2.45 Å is taken as the Wigner–Seitz radius in liquid xenon [51].
As the inner structure of the electron cloud is rather complicated,there are three kinds of simple shapes,which are called ‘Tophat’,‘Dipole’and‘Gaussian’,respectively.Those shapes are always used for the first exploration of the sized atom.The corresponding charge distribution ρ(r),root-meansquare radiusrAtomand the form factorF(q)are shown in the following table

r0in the table is always chosen as the radius of the atom.As talked above,the form factor of the ground state of the Hydrogen atom is a Dipole form.The Helm form factor,which is always used to describe the nucleon shape[52],is in fact a Tophat form.These three kinds of form factors are also used in the puffy dark matter scenario to realize the required velocity dependence in the small cosmological scale[37,38].
The RHF form factor used in XRD differs from the form factors shown in this subsection greatly.We show the corresponding form factorF(q) from the RHF result together with the screened Coulomb (SC) potential,Tophat shape etc for the xenon atom in figure 4.Note that the radiusr0for the Tophat,Dipole and Gaussian shapes is chosen as∼2a0which is taken from [46].The twor0for the SC form factors shown in the figure are tagged with ‘SC0.49’ and‘SC2.45’,respectively.The orange shade in figure 4 shows the interval of momentum transferqfor the detection of light dark matter which will be discussed in the next section.Another thing that should be mentioned is that the Tophat model describes a homogeneous charge distribution within a sphere of radiusr0.We can see from figure 4 and the analytical formula thatF(q) oscillates around zero from an appropriateq.It means that the charge distribution in the momentum space can be negative.This implies that the incident particle can feel an opposite charge of the electron cloud in case of a specific momentum transfer.This is a special phenomenon in the effective scattering theory.
From figure 4,we can see that the factors of the ordinary shapes quickly decrease to zero whenqis greater than the inverse Bohr radius ∼4 KeV.Only the RHF form factor can maintain a large value to a much larger momentum.As discussed in[43],the electrostatic potential cannot be expressed in a simple form equation (6),and the SC form factor equation (7) is not a suitable factor either.RHF form factors are more reliable for realistic applications.This implies that the atoms like xenon have non-trivial shapes for the electron outside the nuclei.F(q) plays a very important role in the scattering of electrons in an atom.The slowly decreasing behavior of the RHF form factor can make the electrons recoils coherently,thus the cloud can receive a large momentum transferqfrom the incident particles.This is contrary to common sense that the cloud only receives the momentum transferqat the order of the inverse radius of the atom.Thus coherent scattering and incoherent scattering are discussed in the following subsection.
2.3.Coherent and incoherent scattering
In order to figure out whether coherent scattering can happen for the electron cloud,here we briefly review the differences between coherent scattering and incoherent scattering[53,54].When an incoming plane wave incident on a radially symmetric potential,the outgoing wave state can be written as
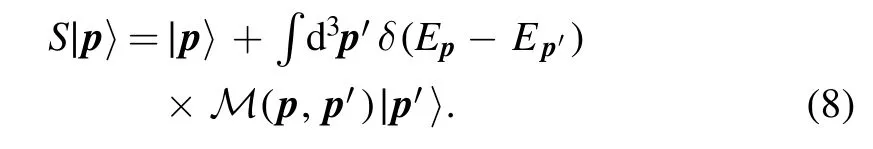
Here M(p,p′)is the scattering matrix elements andSis the usualS-matrix.If the target is composed ofNidentical potentials,and each potential is displaced away from the origin to some location xi≠0,S-matrix for each potential will be transformed by a unitary matrixU=exp (- ix i·p).Then the plane wave scatters to

where the momentum transfer isq=p′ -p.To the lowest order in the perturbation theory,the final state of the scattering is given by summing over all the amplitudes

Therefore the probability of the momentum state ∣p′〉in the final state is proportional to

where Δxij=xi-xj.The expectation value is taken over the N-body internal state of the target.The circumstance is similar to light diffraction which occurs only when the slit is physically the approximate size of,or even smaller than the wavelength of light.For the N-body target,only when the momentum transfer is smaller than the inverse spacing between the potentials,i.e.Δxij·q<1 for alli,j,that every phase in the sum is approximately the same,the scattering will be enhanced coherently.If the spacing is too large,onlyNdiagonali=jelements in equation (11) can survive.Then the incident particle scatters on each target separately,which is incoherent scattering.
From the argument above,we can see that the coherence depends on the space scale.As for the electrons in an atom,whether they can behave as a compact ball at a specific momentum transferqdepends on the spatial scale where the electron cloud locates.Naively thinking,the scale would be the radius of the atom.However,as shown in the last subsection,real electron clouds outside the nuclei have non-trivial shapes.The RHF form factorF(q) does not vanish outside the inverse radius of the atom but decreases slowly with the momentum transferq.In order to show the subtlety,we choose a simple form factorF(q)

which is a homogeneous charge distribution in the momentum space.q0is the border of the distribution,and it is also the typical decreasing point ofF(q).In fact,this is just a‘Tophat’ shape in the momentum space.Obviously,theF(q)decreases to zero atq=q0in this kind of distribution.However,the root-mean-square radius is not at the order of 1/q0,This can be derived from the shape of the charge distribution in coordinate space which is similar
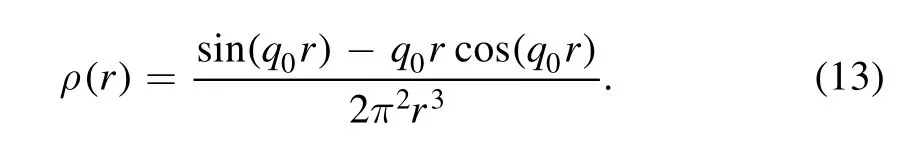
The corresponding ρ(r) is calculated by the Fourier transformation ofF(q),shown in figure 5,in which we choseq0=25 KeV for the demonstration.Note that the unit charge of the target impliesF(q=0)=1,thus the normalization factor of ρ(r) in equation (13) is different from that in the table above.The ρ(r) of the xenon atom numerically calculated from RHF form factorF(q)is shown in the red solid line of the figure.We can see that the negative charge distribution phenomenon discussed in the above subsection come out again.This is interesting and they can be considered effective charge distributions.It means that the incident particle can feel the opposite charge effectively in the coordinate space.From the figure,we can get the following implications.It is true that the charge density decreases quickly outside the typical inverse momentum 1/q0in the Tophat model,while the distribution of the RHF is similar.However,this does not conflict with the measured radius of the atom.We can see that the charge density can maintain the oscillating behavior to a large radius.One can easily check that the root-mean-square radii in both cases are oscillating divergent functions.The results imply that the charge is dominantly located in a very small region near the center of the atom,The requirement of the coherent scattering Δxij·q<1 can be satisfied.Thus the electrons form a compact ball that can receive large momentum transferqand behave like a single particle.Then the non-trivial shape can make the form factor much different from the ordinary consideration.
From figure 4,we can see that xenon RHF form factorF(q)∼0.2 atq=50 KeV.The physics picture for the XRD on this momentum transfer is that the momentum transferqis much larger than the inverse atom radius 1/r0.Since it is a small angle(forward)scatteringQ≫q,the wavelength of the x-ray is much smaller than the radius of the atom.This means that a much smaller x-ray photon that can inject into the interior of the atom can still transfer a much larger momentum to the whole atom and strongly interact with it.Whether such a physics picture can happen in case of an incident of dark matter will be discussed in the next section.
3.Recoil of the electron cloud and its ionization
Compare to the XRD,the key difference in the scattering between the dark matter and the atom may be that the incident particle is massive and slowly moving.However,our focus is the sub-GeV dark matter with a velocity of several hundred kilometers per second O(1 0-3c).Then the de Broglie wavelength for dark matter lighter than 100 MeV can be much larger than the classical radius of the electron.If the interaction between the dark matter and electron is compact,the time scale of the momentum transfer will also be much quicker than the light-crossing time of the electron cloud.The only problem is that the light-crossing time of the slowly moving dark matter is much longer than the x-ray,then nontrivial collision may happen.However,the whole picture is whether the electron cloud can react as a compact ball in the collision process.Figure 4 shows that such compactness can only maintain at a much smaller momentum transfer regimeq<1/r0for the ordinary Tophat,Dipole,Gaussian,or SC shapes.But the RHF results show that the compactness could be reliable to a much largerq.If the compactness maintains,the longer collision time implies the collision can be considered to have higher order contributions from the loop diagram,thus the amplitude must be at sub-leading order.In all,the collision between the dark matter and the electron cloud is analogous to the XRD scattering.The collision between dark matter and the electron can transfer a much larger momentum to the whole electron cloud.The RHF form factorF(q)could be used for the estimation of the momentum transfer and the cross section.In the following,we will give a detailed study of this recoil of electron cloud (REC) to see whether such an estimation is suitable for the exploration of dark matter.

Figure 6.Comparison with ∣fion,e∣2 (green dot), ∣fion,M∣2 (sky blue dash-dot)and ∣fion,C∣2of the xenon atom.For the ionization factor of the electron cloud,the purple line shows the results of the RHF form factor,the orange line shows the result of the ‘Tophat’,and the yellow double dot-dashed line leads to the screened Coulomb potential with the screening length r0=0.49 Å.The maximum q for the REC is shown in the brown dashed line.
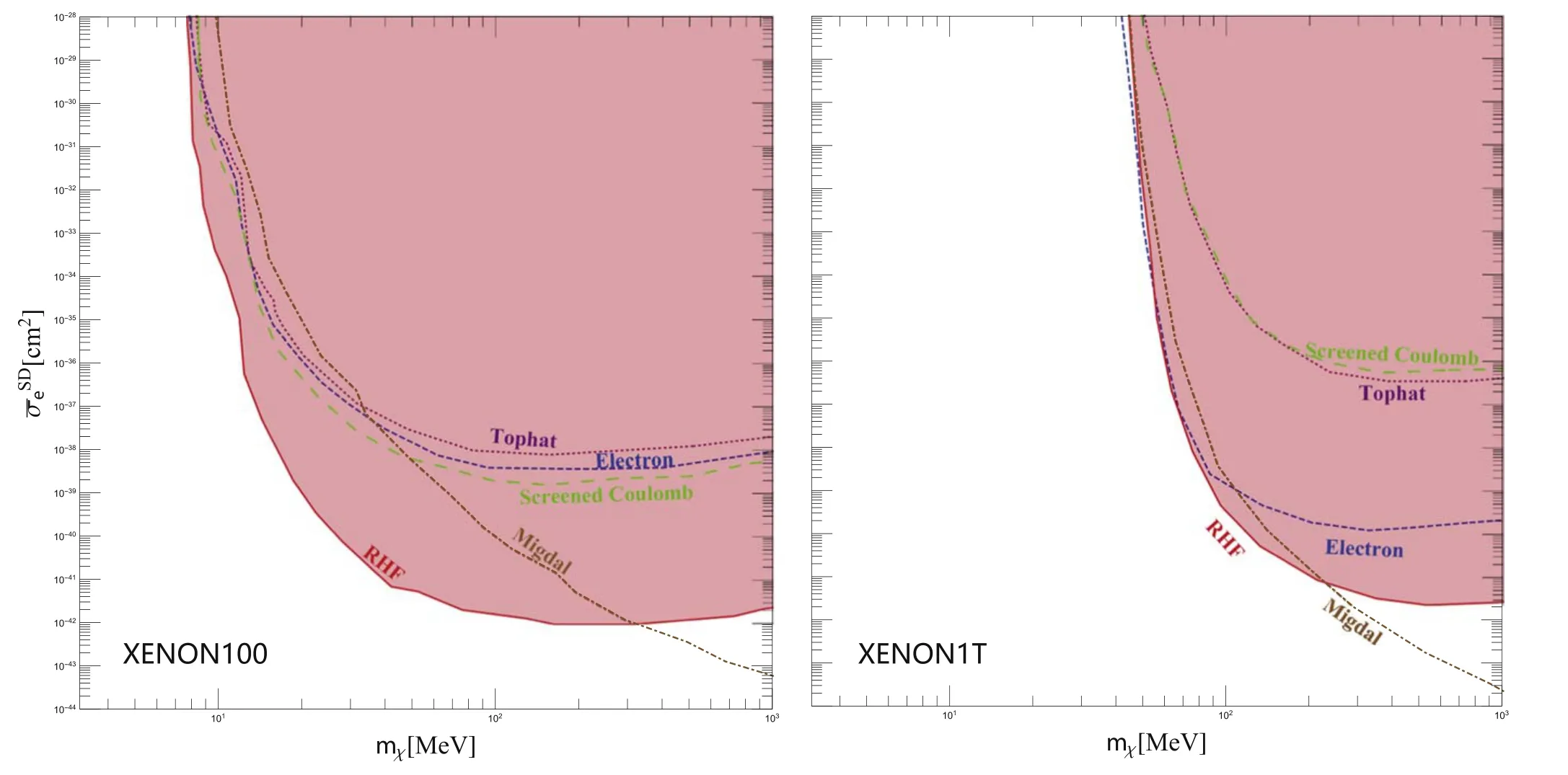
Figure 7.The limits of the cross sections and dark matter mass from Xenon100(left panel)and Xenon1T(right panel).The blue dashed(dotdash)lines show limits on the recoil of a single electron and the Migdal effect.The dotted line shows the result of the Tophat model of the electron cloud,while the long green dashed line gives the exclusion area from the screened Coulomb potential model with the screening length r0=0.49 Å.The shaded regions show the results of the RHF form factor.
In order to compare the Electron ionization via both the Migdal effect and recoil of a single electron,[26] proposed the simpleU(1) extension model of the dark matter which is consist of a dark matter candidate χ and dark photonA′.The′Akinetically mixes with the visible photon.In the work,electron ionization from REC is calculated and compared with the other two processes.Thus the corresponding calculation schemes,such as the Lagrangian,kinetics and dynamics,are similar.We just give some essential points and differences between [26].A detailed calculation can be viewed in [26] and the references within.First,the physical quantity for the comparison is denoted as

It is the fiducial DM-free electron scattering cross section at fixed momentum transferq0=αme,from which μχeis the reduced mass of the χ-esystem.Next,we show the kinetics of the REC and compare it with the Migdal effect and recoil of a single electron.In all these three processes,the incoming and outgoing states are the same:a dark matter particle plus a bound atom and a dark matter particle plus an ionized atom plus an unbound electron,respectively.The incoming dark matter is assumed to be a plane wave,which is both an energy eigenstate and a momentum eigenstate.The incoming atom(at rest in the lab frame) is an energy eigenstate and a momentum eigenstate too.The outgoing dark matter is also a plane wave,and the outgoing atom is in an excited state where the ionized electron belongs to the continuum spectrum of the atomic Hamiltonian.Consider the scattering process of a dark matter particle hitting electron clouds ofZelectrons outside the entire nucleus,for the dark matter particle with massmχ,incoming velocity υ,and outgoing momentump′χ,momentum conservation requires

Note that the recoil energy of the ionized electron is always negligible compared with the momentum transfer.Energy conservation requires the ionized electron to get
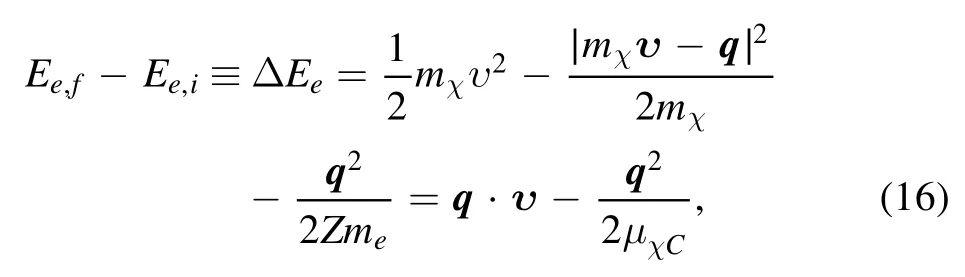
where μχC=Zmemχ/(Zme+mχ) is the DM-Cloud reduced mass.
The kinematics of the Migdal effect,single electron and REC scattering are similar,however,the dynamics differ from each other.They depend on the interacting objects,in other words,on which target the momentum is transferred to the nucleus,electron,or the electron cloud.The interaction term in the perturbation Hamiltonian of the collision between the dark matter and electron cloud withZeis

where xcis the charge distribution position of the electron cloud andMχCis the Lorentz-invariant matrix element for dark matter scattering off electron clouds through 4-momentum transferq≈(0,q).Note that the phase of the charge distribution position eiq·(-xχ+xc) is similar to the phase in equation (11) discussed in the above section.Compared with the recoil of a single electron,what we only need to do is replace the corresponding reduced mass and interaction,etc.As the total charge of the electron cloud isZ,it is obvious that theMχCcan be reduced to a similar interaction as the recoil of a single electron
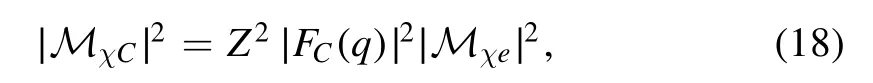
in whichFC(q)is the normalized form factor discussed in the above section.Thus the same reduced cross sectioncan be defined to evaluate both recoils of the single electron and the cloud.In fact,this is the usual way to do the comparison between detection strategies and the target,i.e.spinindependent cross section for different target nuclei.Note that the RHF electron cloud form factor for DM-electron-cloud scattering is used here.The reason for this is that the kinetic mixing between the dark and visibleU(1)gauge field implies that the interactions between the massive dark photonA′ and standard model fermion are proportional to the visibleU(1)charge.This same form factor can be used as shown in [26].
After the cloud is suddenly boosted to a specific velocityvC,it will be dragged by the static nucleus and throw away an ionized electron.As discussed in the above section,it is in fact a similar Migdal effect but happens in a different Galilean frame.Thus the rate of dragging back can be written in a similar formula
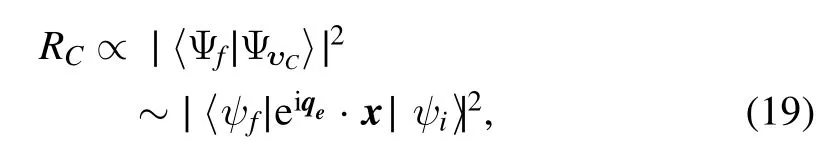
whereΨυCand Ψfare the initial and final states of the wave function of an electron cloud,and they are the single-electron states wave functions.However,being different from the Migdal effect,ΨυCis the cloud with a velocity υC,and the Ψfis the final state of the almost static atom.
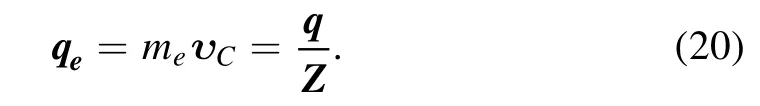
The reason for this estimation is that a compact ball for the electron cloud is adopted in the whole picture,all the electrons in the cloud will move at the same velocity.Note that,though a similarqeis used in both the Migdal effect and REC,theqein the Migdal effect iswhich is much smaller thanqein equation (20),and this will make the phenomenology much different between the two processes.The detail will be discussed in the next section.
The calculation of the ionization rate in REC is also similar to the Migdal effect and recoil of a single electron.We need to integrate over the momentum transfer q and the dark matter velocity v,then sum over the final electronic states Ψfweighted by a delta function enforcing energy conservation.The specific normalization method of summation of final states can be found in [26].
As talked above,the reduced cross sectionis adopted for the calculation of the scattering rate.In fact,the cross section is proposed under the impulse approximation which is related to the free-particle scattering matrix element as the electron recoil spectrum per unit detector mass.The scattering of the dark matter with a single electron can treat the target electron as single-particle states of an isolated atom,described by numerical RHF bound wave functions.The velocityaveraged differential ionization cross section for electrons in the (n,l) shell.


We assume a standard Maxwell–Boltzmann velocity distribution with circular velocity υ0=220 km s-1and a hard cutoff υesc=544 km s-1.Theq-dependence of the matrix element is encoded in the dark matter form-factorFDM(q).The differential ionization rate is written as

whereNTis the number of target atoms and ρχ=0.4 GeV cm-3is the local dark matter density.
The key differences between the REC and the other two processes entirely hide in the ionization form factors,which are independent of all dark matter properties and depend only on the electronic and nuclear structure of the target.For coherent electron clouds scattering,the analogous ionization form factor is
The other two ionization form factor can be found in [26].First,there is an additionalZ2factor compared with the factor of the recoil of a single electron.This is similar to the coherent enhancement in the spin-independent scattering of the nucleus.Another point is thatqein REC will be much larger than theqein the Migdal effect.
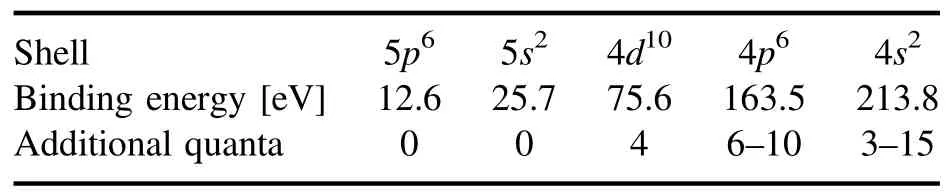
Table 1.Additional quanta of the ionization of xenon.
The numerical calculation of the ionization factor for the Xenon atom can be found in [26].Here we chosemχ=300 MeV,Ee=10 eV andFDM=1 and show the differences between the three processes in figure 6.In order to show the importance of the RHF electron cloud form factor,the results of the Tophat shape and SC0.49are also shown in the figure.The interval ofqis just the shaded region in figure 4.From figure 6,we can see that the RHF form factor gives a much larger ionization form factor than the Migdal effect and the recoil of a single electron.However,the ionization factor of the Tophat shape and the screened Coulomb potential is much smaller than the recoil of the electron.These two factors can be at the same level as the Migdal effect.As we concern,these two models coarsely depict the electron coherent scattering,which is used only as references.The key point is that REC could dominate the ionization if wetake the RHF form factor seriously.Another three points should be addressed:
1.As shown in figure 6,∣fion,e2∣decreases quickly with theq,thus the rate of recoil of a single electron is dominated by a smallqregion.
2.∣fion,M∣2increases with the growth ofq,thus the rate is dominated by largeqregion.Nevertheless,as themχwe considered is much lighter than the mass of the nucleus,the reduced mass of the collision mainly proportional tomχ.Sinceqein this effect are much smaller thanq,the ionization factor does not feel any suppression factor in the region of the integration.
3.The above two items are already addressed in [26],the RHF ∣fion,C∣2is larger than the other two ionization factors.However,the upper limit ofqis

for a dark matter much heavier than the mass of the xenon cloud.Note thatυmaxis taken as usual 770 km s-1in the above equation.
With these ionization form factors,we can calculate the scattering rate and get the limits on the scattering cross section which will be discussed in the next section.
4.Numerical limits from the experimental detection
Following the procedure in [7],we numerically calculate the limits on the spin-independent scattering cross section from the experimental XENON100 data[55,56](30 kg years)and XENON1T data [57] (1.5 tones years).The recoil energyEecan induce both of the observed electronsneand scintillation photonsnγ.The numbers of quantan(1)that are produced by the step energyW=13.8 eV which isn(1)=Floor(ER/W).The probability of the initial electron recombining with an ion is assumed asfR=0.The fraction of the primary quanta observed as the electrons is taken asfe=0.83.The corresponding uncertainties are chosen as 0 Figure 7 shows the numerical results of the limits from Xenon100 (left panel) and Xenon1T (right panel) data.The results of limits on the recoil of a single electron and the Migdal effect are also shown for comparison.We can see that,in the range ofmχ≿100 MeV,the limits of the RHF form factor are much more stringent than the recoil of a single electron,almost 4 orders stronger.This can be easily understood that the coherent enhancement ofZ2(542) factor and a sufficiently large RHFF(q) in the interval of the rate integral equation (21).The limits on the Tophat model and screened Coulomb potential model are in the same order as the results from the recoil of a single electron under Xenon100 experiment data.However,they are negligible to the recoil of a single electron under the constraints of Xenon1T experiment data.The limits on the RHF form factor in both cases are much more stringent than the limits of recoil of a single electron,Tophat,and screened Coulomb potential,due to the RHFF(q).Note that,we can’t distinguish all these three processes (REC,single electron and Migdal effect) in experiments now,because the number of PE generated is observed in the experimental results,and these three processes cause the electron to ionize out and generate corresponding numbers of PEs as S2 signals.It is unable to tell which physical process produces these PEs.Since the recoil of a single electron and REC originate from the same darkU(1)interaction,thus we just added together both recoils,so that the summation gives more comprehensive limits on the cross sections.The constraints of the Xenon1T data released below the 100 MeV,however,the Xenon100 data can maintain the constraints to about 10 MeV.The reason for this can be shown in figure 8 which shows the observed events versus PEs from the Xenon100 and Xenon1T experimental data.The left panel shows theandmχ=100 MeV result for Xenon100,and the right panel shows theandmχ=200 MeV results for Xenon1T.One can check that,the lighter dark matter(<100 MeV)in the recoil of a single electron and REC mainly cause different distribution in small PE number regions.In the numerical calculation,we choose[80,190]PE bins of the Xenon100 for the constraints,while we choose [165,275] PE bins of the Xenon1T for the constraints.Thus the Xenon100 gives a better performance when the dark matter mass is lighter than 100 MeV. Figure 8.Observed events versus PEs from Xenon100 (left panel) and Xenon1T (right panel) data,for Xenon100mχ=100 MeV and while for Xenon1T, As for the comparison with the Migdal effect,the limits on the RHF form factor are more stringent than the Migdal effect below about 400 MeV (200 MeV) from Xenon100(Xenon1T) data.The reason has been addressed above that the upper limit of the rate integral equation (21)qmaxin the Migdal effect can extend to a much larger value when the dark matter mass is much lighter than the target nucleus.The ionization form factor can grow up to a sufficiently large value.Thus,the Migdal effect gives a better performance in heavy dark matter regions. The search for sub-GeV dark matter is a hot topic at the cutting edge of physics research.However,as the sensitivity is lost for the light dark matter detection,the traditional strategies for detecting WIMP-type dark matter are no longer feasible.A novel detection are proposed that the electron cloud is boosted by the dark matter and throws away an electron when it is dragged back by the heavy nucleus,namely the coherent scattering of the electron cloud of the atom.The processes can be considered as a similar Migdal effect but in a different Galilean frame.Though the form factorF(q) decreases quickly with the multiplicative inverse of the radius of the atom,as shown in the simple Tophat,Dipole,Gaussian shape and the SC model,this effect is still not negligible compared with the recoil of a single electron and the Migdal effect.What’s more,the survey in the XRD shows that the atomic form factor are much more complicated than the naive consideration.The results of the RHF method give non-trivial shapes of the atom.We show that the corresponding form factors do not conflict with measured radii in the coordinate space.We also show that the collision between the sub-GeV dark matter and the electron cloud is similar to the XRD.At least,it should be attempted to apply the RHF form factor in the estimation of the scattering rate of the dark matter detection. Having been equipped with the RHF form factor and impulse approximation,we proceed to show the detailed calculation of the recoil of the electron cloud.The kinetics,the fiducial cross section and the corresponding calculation of detection rate are given analytically.After that,we show the constraints on the cross section from the current experimental measurements.The Xenon100 and Xenon1T data are adopted for the constraints.The comparison between the other two processes is also discussed.We found that the limits of the RHF form factor are much more stringent than the recoil of a single electron,almost 4 orders stronger.The constraints of the Xenon1T data are released below the 100 MeV,however,the Xenon100 data can maintain the constraints to about 10 MeV.The limits on the RHF form factor are more stringent than the Migdal effect below about 400 MeV(130 MeV) from Xenon100 (Xenon1T) data,due to the extended interval of the rate integration.Another thing that should be emphasized is that the recoil of a single electron and the recoil of the electron cloud originate from the same fundamental interaction,thus in principle,both recoils should be added together and the summation gives more comprehensive limits on the cross section. The process we proposed and the corresponding results seem promising and novel.However,the key point of our work is whether the RHF form factor can be used in the detection of dark matter,which we only have a neutral attitude towards. Acknowledgments We thank Nick Houston,Lei Wu and Bin Zhu for their helpful discussions.This work was supported by the Natural Science Foundation of China under Grant number 11775012.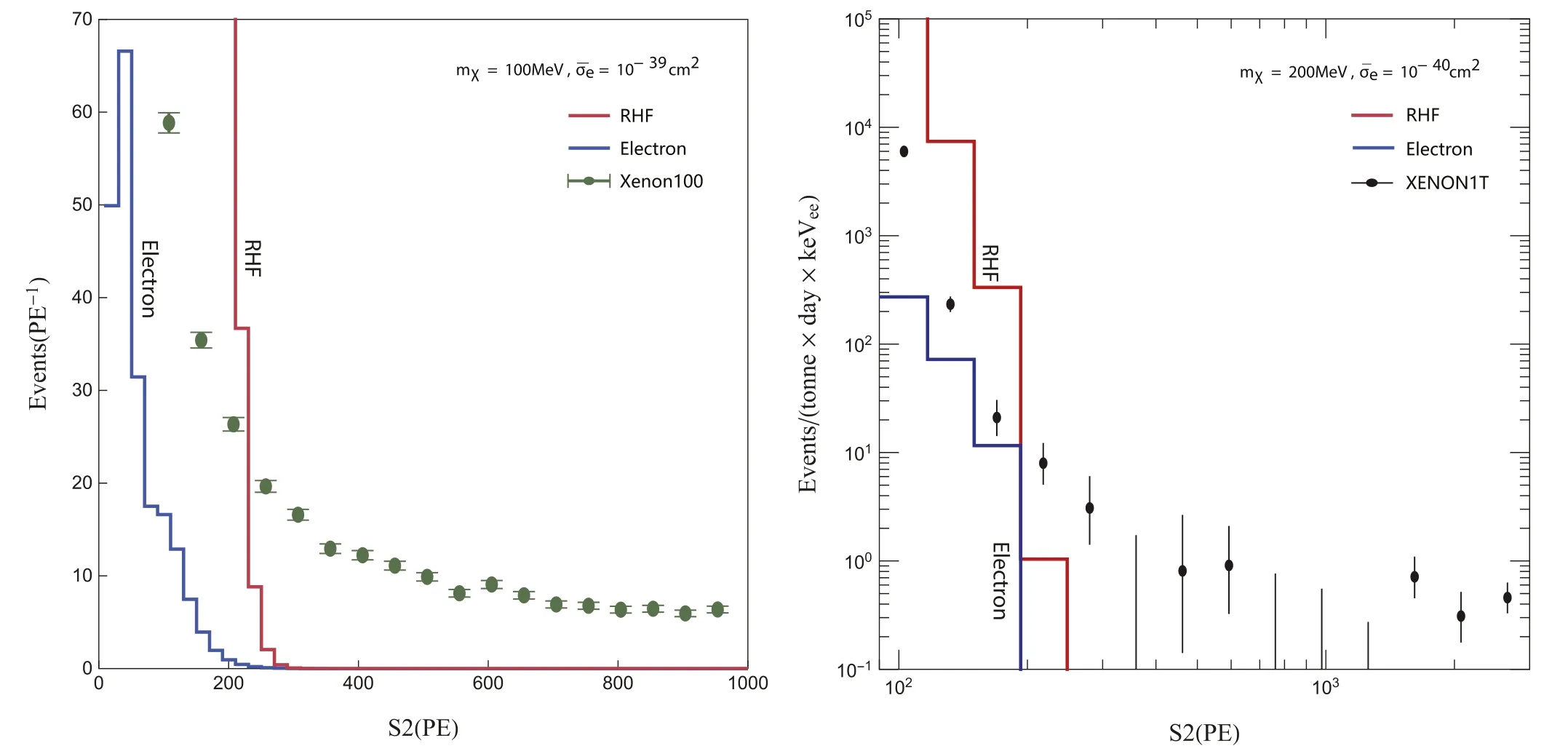
5.Conclusion
杂志排行
Communications in Theoretical Physics的其它文章
- A numerical method to calculate dwell time for electron in semiconductor nanostructure
- Thermal Hall conductivity with sign change in the Heisenberg–Kitaev kagome magnet
- Dimensional crossover of a Rabi-coupled two-component Bose–Einstein condensate in an optical lattice
- Modification of laser-induced state in atomic attosecond transient absorption by the XUV pulse pair
- Optical forces on neutral atoms in the presence of fluctuating laser fields:numerical analysis
- High-sensitive refractive index sensing and excellent slow light based on tunable triple plasmon-induced transparency in monolayer graphene based metamaterial
