Direct measurement for general quantum states using parametric quantum circuits

Zhiyuan Wang,Zijing Zhangand Yuan Zhao

Department of Physics,Harbin Institute of Technology,Harbin 150001,China

Abstract In the field of quantum information,the acquisition of information for unknown quantum states is very important.When we only need to obtain specific elements of a state density matrix,the traditional quantum state tomography will become very complicated,because it requires a global quantum state reconstruction.Direct measurement of the quantum state allows us to obtain arbitrary specific matrix elements of the quantum state without state reconstruction,so direct measurement schemes have obtained extensive attention.Recently,some direct measurement schemes based on weak values have been proposed,but extra auxiliary states in these schemes are necessary and it will increase the complexity of the practical experiment.Meanwhile,the post-selection process in the scheme will reduce the utilization of resources.In order to avoid these disadvantages,a direct measurement scheme without auxiliary states is proposed in this paper.In this scheme,we achieve the direct measurement of quantum states by using quantum circuits,then we extend it to the measurement of general multi-particle states and complete the error analysis.Finally,when we take into account the dephasing of the quantum states,we modify the circuits and the modified circuits still work for the dephasing case.

Keywords: direct quantum tomography,quantum state measurement,quantum circuits,quantum gates

1.Introduction

In order to obtain the information of an unknown quantum state,we need to perform a complete measurement of the target quantum state,that is,quantum state tomography(QST).In the standard QST,a set of complete measurement bases and a state reconstruction algorithm are essential.However,with the expansion of the dimensions of quantum systems,the number of measurement bases required by QST increases exponentially.This will increase the complexity of the actual experiment because QST is a global reconstruction of all the information of the quantum state.Due to the existence of statistical errors,optimization methods are usually used to reconstruct the target quantum state,which is closest to the probability distribution of the measurement results [1,2].

But in some cases,such as the verification of quantum entanglement [3] and quantum coherence [4],we only need partial information of the quantum state,so the traditional QST will be complex.Direct measurement schemes allow us to only obtain the information we are interested in because it does not require a global quantum state reconstruction.This will reduce the complexity of the practical experiment.Direct tomography schemes based on weak measurements have been developed recently [5–10].In addition to important applications in the field of precision measurement [11–15],weak measurements also play an important role in direct measurement schemes.Lundeenet al[16] used weak measurements to directly measure the spatial wave function of photons.Maliket al[17] used the scheme to realize the direct measurement of 27-dimensional wave functions of photon orbital angular momentum.Wuet al[18] proposed a scheme for direct measurement of partial elements in general quantum states.Renet al[19] proposed a weak measurement scheme for directly measuring arbitrary elements of a state density matrix,and extended it to the direct measurement of the multi-particle density matrix.Subsequently,in order to make up for decreased measurement precision caused by weakcoupling approximation in weak measurement,strong measurement schemes have also been proposed one after another[20–22].But even so,direct measurement schemes based on weak or strong measurements require the coupling between target quantum states and extra auxiliary states,so it will increase the complexity of practical experiments.In addition,since there is a post-selection process in the measurement,it will consume a lot of measurement resources and reduce the utilization.

In order to avoid the disadvantages of weak-value-based schemes,this paper proposes a direct measurement scheme without auxiliary states for a single-particle system.Subsequently,we extend this scheme to the direct measurement of a multi-particle system.Since our scheme does not require auxiliary states and post-selection process,it will reduce the complexity of practical experiments.Meanwhile,our scheme is easy to be expanded and integrated,which is helpful for the realization of direct quantum tomography in integrated quantum chips.The paper is organized as follows: in section 2,we propose a direct quantum tomography scheme without auxiliary states for arbitrary systems and complete the error analysis in section 3.Finally,in section 4,when we take into account the dephasing of quantum states caused by noise channels,we modify the circuits and the modified circuits are still applicable to the dephasing situation.

2.Quantum circuits for directly measuring the general quantum states

In this section,we first introduce a direct measurement scheme without auxiliary states for single-qubit systems.We then generalize it to arbitrary multi-qubit systems.To demonstrate the advantages of circuit schemes,we compare this scheme with a direct measurement scheme based on weak measurements.In the weak measurement scheme,in order to realize the direct measurement of a single-qubit unknown state,two auxiliary states and two couplings need to be used as shown in figure 1(a).For direct measurement of multiple qubits,we will need more auxiliary states and couplings,which will increase the complexity of practical experiments.In addition,in some physical systems,these required auxiliary states are not easy to be constructed [19],and the required couplings are not easy to achieve,which will limit the application of weak measurement schemes.In our circuit scheme shown in figure 1(b),auxiliary states are not necessary and the required basic quantum gates are already implemented well by many physical systems,so this will reduce the complexity of practical applications.Next,we will show in detail how our scheme works.

As for a single-qubit state,we could describe this quantum system with a density operator,i.e.wherem,n∊{0,1}.Since the density operator is a Hermitian operator,soθnn=0,θmn=-θnm,λmn=λnm.To obtain the diagonal elements of the density operator,we can directly use the projective operator∣n〉 〈n∣.However,it is a challenge to measure non-diagonal elements because the operator∣m〉〈n∣(m≠n)is not a Hermitian operator.At this point,we can use the scheme shown in figure 1(b)to obtain non-diagonal elements.In this scheme,we need to perform a phase shift operation on the target quantum state,and its operator can be expressed as

Next,we generalize this scheme to the measurement of arbitrary multi-qubit systems.Multi-qubit states can exhibit quantum entanglement and quantum nonlocality,so measuring a multi-qubit system will become complicated.As we all know,a multi-qubit system can be expressed as=wheres,1At this time,the singlequbit phase-shift gate we need is extended to a multi-qubit phase-shift gate (see figure 2).The expression for this multiqubit phase-shift gate is

After completing the projection measurement,we can get t heprojection probability as

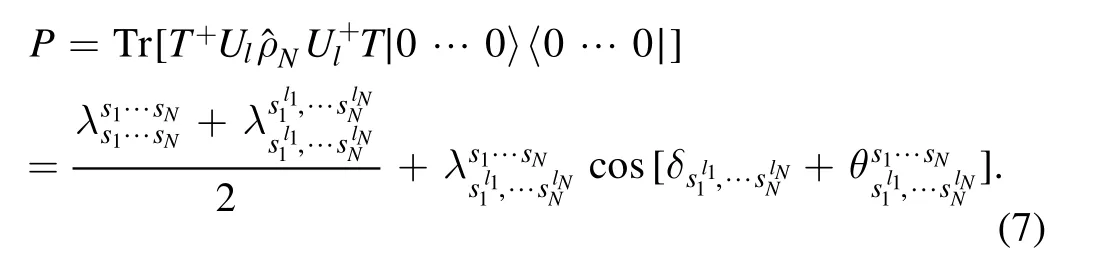
Similarly,when we choose the imposed phase shiftsδlas 0,π2,π,3π2,we denote the corresponding projection probability asP0,Pπ/2,Pπ,P3/π2,respectively.We then can obtain the real and imaginary parts of arbitrary off-diagonal matrix elements like equations (4),(5).

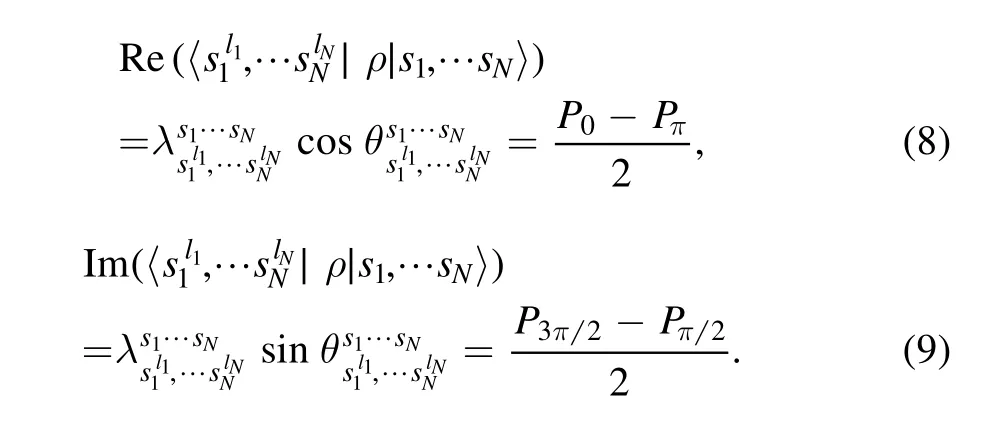
In order to show our circuit scheme more clearly,here we take a three-qubit system as an example to show the circuit scheme how to work.When the matrix elements we need to measure are 〈 100 ∣ρ∣110〉,〈 010 ∣ρ∣101〉,〈 000 ∣ρ∣011〉,and〈 000 ∣ρ∣010〉,we only need to perform these circuits shown in figures 3(a)–(c) respectively.

It is worth mentioning that this scheme is also applicable to high-dimensional quantum state systems,namely qudit systems,such as photon orbital angular momentum.We only need some corresponding high-dimensional quantum gates to implement the circuit structure in figure 2 to obtain any specific matrix elements of the high-dimensional quantum system.Since the measurement steps are similar to those infigure 2,here we directly give the direct measurement circuit of the high-dimensional qudit systems (see figure 4).

3.Error analysis of direct measurement scheme

As for the value ofa0,we can directly obtain it by a Pauli measurement∣0 … 0〉〈0 …0 ∣.According to the error transfer formula,we can get the measurement errorΔAiRandΔAiIas follows

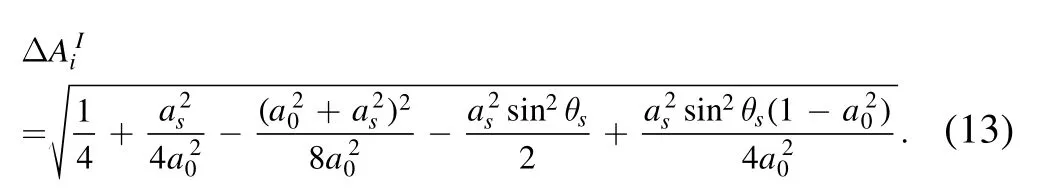
According to Fisher information theory,we can get the Cramér–Rao bound of the measurement error asThe Cramér–Rao bound defines the minimum measurement error that can be achieved in our parameter measurement process,and it determines the lower bound of measurement error.If the measurement error of our scheme is close to the Cramér–Rao bound,it indicates that our scheme has a high measurement precision.

Figure 5(a) shows the relationship among the ratioasandθs.When we fxi the value ofas,we can see periodic changes of the ratiowhich can be verified by equation (13).It can also be seen that when the values ofasandθsare within a certain range,the measurement precision of our circuit scheme can be very close to the Cramér–Rao bound,and similar results are shown in figure 5(b).

Figure 1.Two schemes for directly measuring single-qubit systems.(a) A weak measurement scheme for directly measuring specific matrix elements.In this scheme,additional auxiliary states need to be used,and more auxiliary states are needed when the target quantum state is a multi-particle system.(b) A circuit scheme without auxiliary state.Here Ul(δ)represents a single-qubit phaseshift gate,and R+y represents a rotation gate,satisfying=exp (i π ).is an inverse operator of the operator Ry.

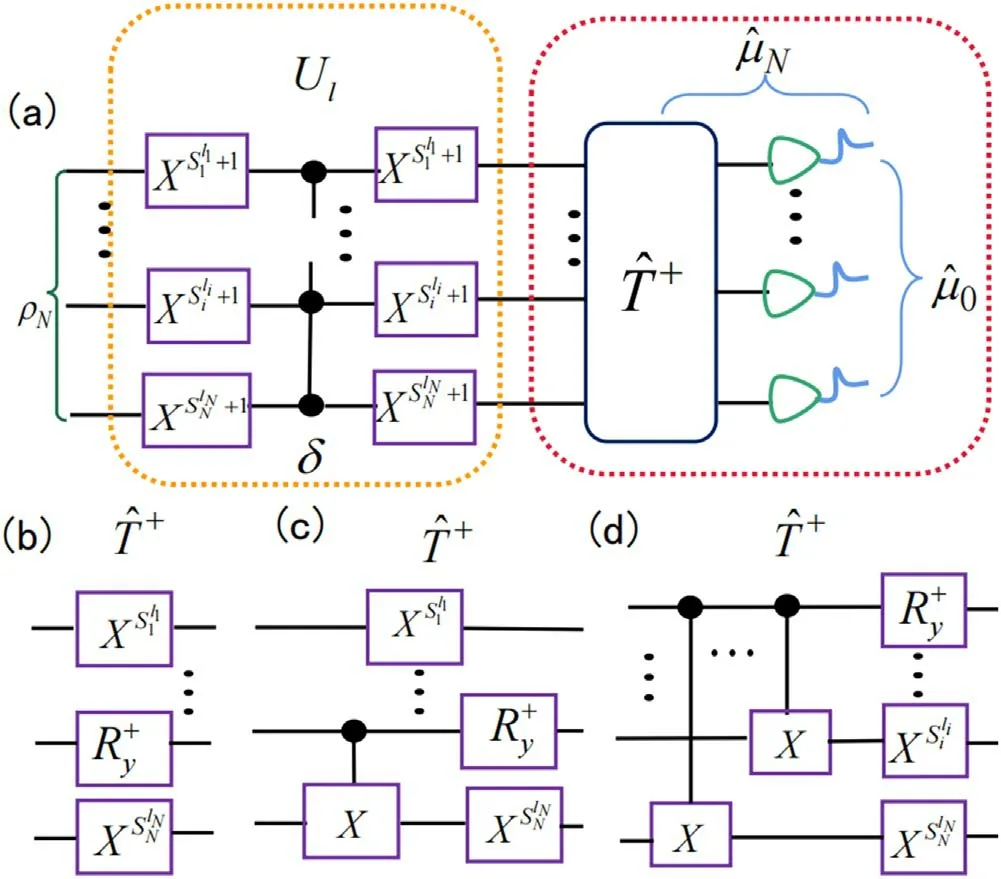
Figure 2.A circuit scheme to realize the direct measurement of arbitrary multi-qubit systems.(a)A complete operation flow;(b)The circuit structure of the operator T +when the state∣φN 〉is a direct product state (c) The circuit structure of the operator T+ when the state∣φN 〉is partially entangled.(d) The circuit structure of the operator T+ when the state∣φ 〉N is fully entangled.Here X represents a single-qubit NOT gate.

Figure 3.Circuit schemes of measuring specific matrix elements for a three-qubit system.(a)is the quantum circuit that directly measures the matrix element 〈100 ∣ρ∣110〉.(b) is the quantum circuit that directly measures the matrix element 〈010 ∣ρ∣101〉.(c) is the quantum circuit that directly measures the matrix element〈 000 ∣ρ∣011〉.(d) is the quantum circuit that directly measures the matrix element〈000 ∣ρ∣010〉.

Figure 4.(a) A circuit diagram for direct measurement of a ddimensional(d >2) quantum system.The measurement flow is similar to the steps in figure 2.In this scheme,some highdimensional single-qudit gates and two-qudit controlled-NOT gates are used. XdSi and +Rd are respectively a single-qudit NOT gate and a single-qudit rotation gate,satisfying and Here,the subscript d represents a d-dimensional quantum system.(b) The circuit structure of the operator Td+ when the state∣φN〉d is a direct product state.(c) The circuit structure of the operator Td+ when the state∣φN 〉d is partially entangled.(d)The circuit structure of the operator +Td when the state ∣φ 〉N d is fully entangled.

Figure 5.(a) The ratio Δ/ΔAiRas a function of as andθs.(b)The ratio Δ/ΔAiIas a function of as andθs.Here a0 is chosen to be 0.2.

Figure 6.(a) Quantum circuits with dephasing channels.(b)Quantum circuits for measuring multi-qubit pure states when dephasing is considered.The original auxiliary state is∣0〉.Here,H represents a Hadamard gate.

4.Quantum circuits of direct measurement against dephasing

Two-level systems are often commonly used in quantum information.The entangled pure states of multi-qubit are important resources in the field of quantum information.However,an entangled pure state,the expression of which satisfiesis easy to be affected by noise.In this section,we will analyze the impact of environmental noise on the target quantum state and propose corresponding solutions.In the measurement process of multi-qubit pure states,due to the existence of noisy channels between part A and part B (see figure 6(a)),dephasing will occur in the target quantum state.At this time,the nondiagonal elements of the density matrix of the target quantum state will gradually degenerate,so that we cannot get the phase values of expansion coefficients of the multi-qubit pure states.After dephasing,the output quantum state at this time becomesThere are only diagonal elements in the density matrix and we will not observe the phase values of expansion coefficients even if we perform a projection measurement.At the same time,the quantum Fisher information of the phase measurement is also 0.In order to obtain the phase information of the target quantum state under the condition of dephasing,we modify the circuits in section 2 (see figure 6(b)).

In the modified circuits,we use an auxiliary qubit to complete the direct measurement scheme in the dephasing situation.At this time,the joint quantum state of the auxiliary qubit and the target quantum state after the operationUi(δ)is expressed as

Next,a multi-qubit controlled-NOT gate is used to realize the coupling between the target state and the auxiliary state,and at this time the joint quantum state becomes

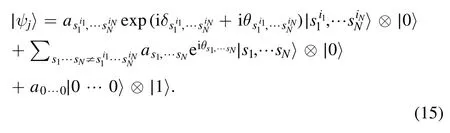
Subsequently,we perform a post-selection process on the target quantum state,the purpose of which is to pick up the target eigenstateand eigenstate∣00 … 0〉,so the expression of the post-selection state we need is as follows

We can see that the information of the target amplitude and phase is transferred to the auxiliary state.Finally,we perform a Hadamard gate operation on the auxiliary state after postselection and its quantum state evolves into

Next,dephasing will occur when the state∣φ′〉passes through the noise channels.We use the Kraus operatorEkto describe the dephasing effect,and the density matrix of the auxiliary qubit after dephasing is expressed as

The expressions ofE0andE1are as follows,pis the probability of dephasing

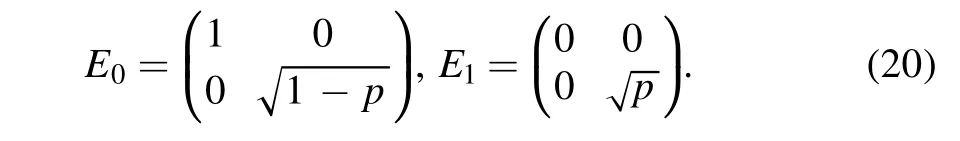
Figure 7 shows the relationship between matrix elements of the auxiliary qubit after dephasing and the imposed phase shift and figure 8 shows the relationship among the Fisher information after complete dephasing,the probability amplitude and the imposed phase shift.Whenp=1,the density matrixρ′ of the auxiliary state evolves into

Figure 7.Matrix elements of the auxiliary qubit after dephasing as a function of the imposed phase shiftδs.Here, p=0 and θs=π3.

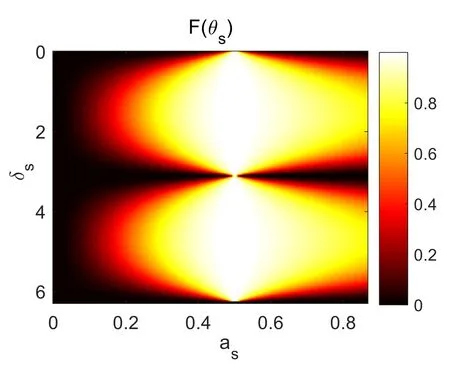
Figure 8.Quantum Fisher information of auxiliary states after complete dephasing.It can be seen that the Fisher information of the auxiliary state after the H gate operation is not 0.At this time,we can perform a Pauli measurement on the auxiliary state to obtain the target phase.

Figure 9.The ratioFQ (θs)/Q(θs)as a function of the probability amplitude as.Although the quantum Fisher information of this scheme cannot be fully recovered,its Fisher information is always greater than 0 at least,which means that we can still obtain the target phase by projection measurement at this time.

According to the expression ofρ′,we can see that even if the quantum state is completely decoherent,the phase information still can be obtained due to the H gate operation.Finally,the dephasing density matrix is measured by using a Pauli measurement operator=∣0〉 〈0 ∣.We then can get the projection probability satisfies

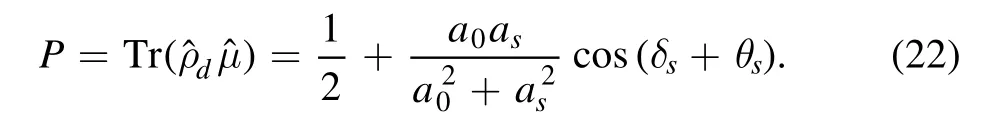
We can see that the projection probability at this time is related to the phaseθs.Next,we can get the value of the target phaseθsby choosing an imposed phase shiftδs.We then use the quantum Fisher information theory to analyze the phase measurement precision at this time.It can be seen that compared with the previous circuits,the H gate in the modified circuits always keeps the quantum Fisher information nonzero for phase measurement.If there is no H gate,there will be no phase information in the dephasing density matrix.For the density matrixρ′,its quantum Fisher information can be described by the following equation [23]

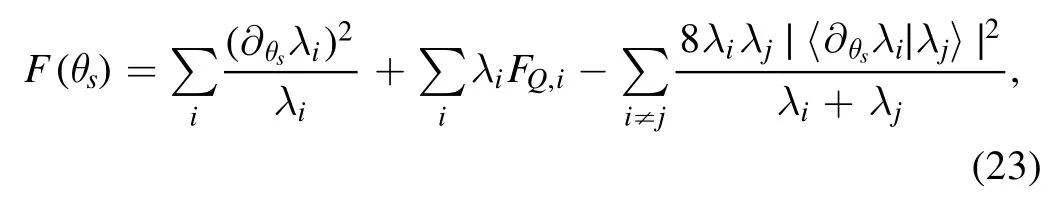
where∣λi〉 is the eigenstate of the density matrixρ′,and itscorresponding eigenvalue isλi,In equation (23),The corresponding quantum Fisher information of the eigenstate∣λi〉satisfiesIt can be seen from equation(21)that when the dephasing occurs completely,the quantum Fisher information of the density matrixρ′about the target phaseθsis

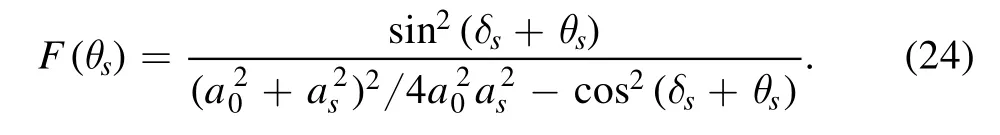
Since our scheme only measures the auxiliary states with successful post-selection,the Fisher information of the whole process satisfiesFQ(θs)=pfF(θs)+Fpf.The successful probability of post-selection is independent of the phaseθs,soFpf=0,then we can getFQ(θs)=pfF(θs).When the dephasing does not occur,the quantum Fisher information about the target phaseθsby using the scheme in figure 2 isAs shown in figure 9,the ratiois always greater than 0,which means that we can still obtain the target phase even if a dephasing situation occurs.

5.Conclusion

In this work,a direct measurement scheme of quantum states without the assistance of pointer states is proposed.Compared with previous weak-value-based schemes,it simplifies the practical experimental procedures while eliminating the need for a post-selection process.This scheme can obtain arbitrary specific elements of the state density matrix.Meanwhile,when we consider the dephasing in the target quantum state,we modify the scheme,and the modified scheme is still applicable to the dephasing situation.This scheme is easy to be expanded and integrated,laying the foundation for the realization of direct quantum tomography in integrated quantum chips.

Acknowledgments

This research was supported by National Natural Science Foundation of China (62075049) and (61701139).

Disclosures

The authors declare no conflicts of interest.