Higher-order rogue waves with controllable fission and asymmetry localized in a (3+1)-dimensional generalized Boussinesq equation

Sheng Zhangand Ying Li

School of Mathematical Sciences,Bohai University,Jinzhou,China

Abstract The purpose of this paper is to report the feasibility of constructing high-order rogue waves with controllable fission and asymmetry for high-dimensional nonlinear evolution equations.Such a nonlinear model considered in this paper as the concrete example is the (3+1)-dimensional generalized Boussinesq (gB) equation,and the corresponding method is Zhaqilao’s symbolic computation approach containing two embedded parameters.It is indicated by the (3+1)-dimensional gB equation that the embedded parameters can not only control the center of the first-order rogue wave,but also control the number of the wave peaks split from higher-order rogue waves and the asymmetry of higher-order rogue waves about the coordinate axes.The main novelty of this paper is that the obtained results and findings can provide useful supplements to the method used and the controllability of higher-order rogue waves.

Keywords: higher-order rogue wave,controllable fission and asymmetry,symbolic computation approach,(3+1)-dimensional gB equation

1.Introduction

Rogue waves were originally used to describe the extremely destructive water waves on the ocean,which appeared from nowhere and disappeared without a trace [1].From the point of view of mathematics,rogue waves are a kind of special non-singular rational solutions of nonlinear evolution equations.In 1965,the concept of ‘freak rogue waves’ was first proposed by Draper [2].Since then,the study of rogue waves has attracted widespread attention like those [3–19]and some effective methods have been proposed for constructing rogue wave solutions,such as Darboux transformation [4,6,7],Hirota’s bilinear method [8,9],inverse scattering transform [10,11] and so on.To be more specific,Solli,Ropers,Koonath and Jalali[3]reported the rogue waves observed by them in the optical system and modelled the generation of these rogue waves through the generalized nonlinear Schrödinger (NLS) equation;Akhmediev,Ankiewicz and Soto-Crespo [4] presented a modified Darboux scheme for constructing rogue wave solutions of the standard self-focusing NLS equation;Yan [5] gave the term ‘financial rogue waves’ based on the nonlinear option equation;Guo,Ling and Liu [7] proposed the generalized Darboux transformation to constructNth-order rogue wave solutions of physically interested models and illustrated its feasibility with two concrete examples;Ohta and Yang[8]derivedNth-order rogue wave solutions of the NLS equation by Hirota’s bilinear method;Randoux,Suret and El [10] used a local periodization procedure to give inverse scattering transform analysis of rogue wave solutions of the NLS equation;Ma [16] presented the polynomial conjecture related to rogue waves in the Korteweg-de Vries equation.

More recently,some researchers [20–27] have focused on studying rogue wave solutions,especially higher-order rogue wave solutions of (3+1)-dimensional nonlinear models.In 2018,Zhaqilao [22] proposed the so-called symbolic computation approach to constructing rogue wave solutions with controllable centers of two high-dimensional nonlinear systems.Compared with the other methods [4,8,10],the symbolic computation approach [22] is direct and does not depend on the τ-function and Lax pair analysis which require high skills.More importantly,a pair of parameters embedded in the method [22] has been proven to be able to control the centers of rogue waves in terms of position and quantity.It is worth mentioning that the method [22] without these two parameters is only its initial version [21].In this paper,we find that in addition to controlling the center of a first-order rogue wave,these two parameters can also control the fission and asymmetry of higher-order rogue waves.However,the findings on fission and asymmetry of higher-order rogue waves are not reported in [22].Since the high asymmetry is another prominent feature of rogue waves besides steepness and instantaneity,it is of great significance to construct asymmetric rogue waves.Although there are a few studies on asymmetric rogue waves,such as[28–30],these studies either stay on the image display or have no substantive discussion on the regularity of control factors.In this article,we shall use the method [22] to construct higher-order rogue wave solutions with controllable fission and asymmetry of the following(3+1)-dimensional generalized Boussinesq (gB) equation[27]:

whereα,βandγare constants,and the influence laws of two parameters controlling the fission and asymmetry of higherorder rogue wave solutions are discussed.In 2019,Yan [27]bilinearized equation (1) and obtained its two-soliton solutions based on Bell polynomial theory.Meanwhile,Yan [27]also obtained a breather wave solution and first-order rogue wave solution of equation (1) by using the extended homoclinic test method.As far as we know,the higher-order rogue wave solution of equation (1) and its fission and asymmetry has not been reported.

We arrange the rest of this paper as follows: section 2 describes Zhaqilao’s symbolic computation approach [22];section 3 gives the Painlevé analysis and bilinear form of equation(1);in section 4,the first-,second-,third-and fourthorder rogue wave solutions of equation(1)are constructed by the method [22],and then the effects of the two parameters included in the constructed rogue wave solutions on the center,fission and asymmetry of the rogue waves are discussed;and section 5 concludes this paper and discusses the potential physical applications of the results obtained.

2.Description of Zhaqilao’s symbolic computation approach

To construct rogue wave solutions of the(3+1)-dimensional gB equation (1),we first recall Zhaqilao’s symbolic computation approach [22].For a given (3+1)-dimensional nonlinear partial differential equation (PDE) assumed as:

wherePis usually a polynomial ofuand its various partial derivatives with respect tox,y,zandt,or any other expression which can be transformed into such a polynomial,we outline the steps of the method [22] as follows:

Step 1.Based on the Painlevé analysis,we take a transformation:

wherefis an undetermined function of the independent variablesx,y,zandt;

Step 2.With the help of equation (3),we assume that equation (2) can be transformed into the following Hirota’s bilinear form:

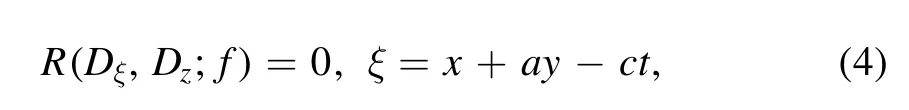
whereaandcare undetermined real constants,DξandDzare Hirota’s operators [31]:

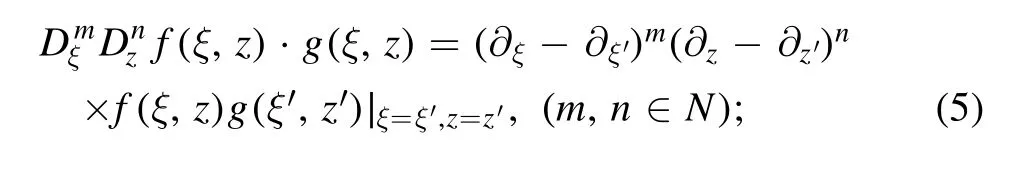
Step 3.We suppose that

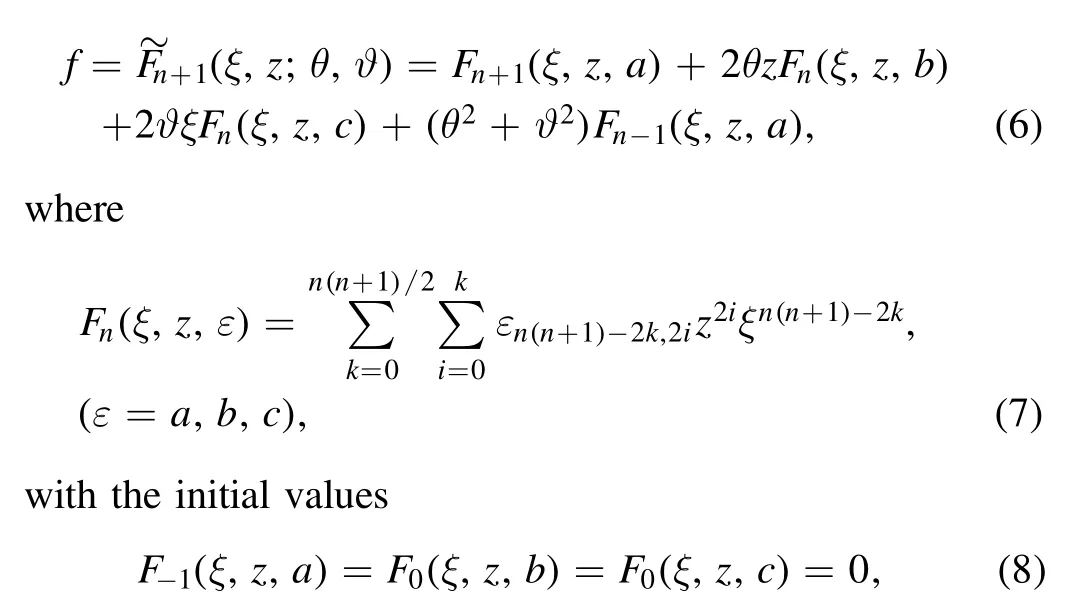
whileaj,l,bj,landcj,l(j,l∊{0,2,4,···,n(n+1)})are all real undetermined constants,θandϑare two embedded parameters in the rogue wave solutions to be constructed.

Step 4.Substituting equation (6) into equation (4),and then setting all the coefficients of the same powers ofzpξq(p,q=0,1,2,···)to be zeros,we can derive a system of polynomial equations foraj,l,bj,landcj,l(j,l∊{0,2,4,···,n(n+1) }).

Step 5.Solving the system of polynomial equations derived above and substituting the obtained values ofaj,l,bj,landcj,l(j,l∊ {0,2,4,···,n(n+1)})into equation (7),we get some rational solutions of equation (2) by means of equations (3) and (6),and from which the first-,secondand other higher-order rogue wave solutions localized inξandzcan be obtained.

3.Painlevé analysis and bilinear form

Theorem 3.1.By Painlevéanalysis,the following auto-Bäcklund transformation for the(3+1)-dimensional gB equation(1)can be derived:

whereu0is a solution of equation(1),while the real functionφofx,y,zandtsatisfies the system of nonlinear PDEs:

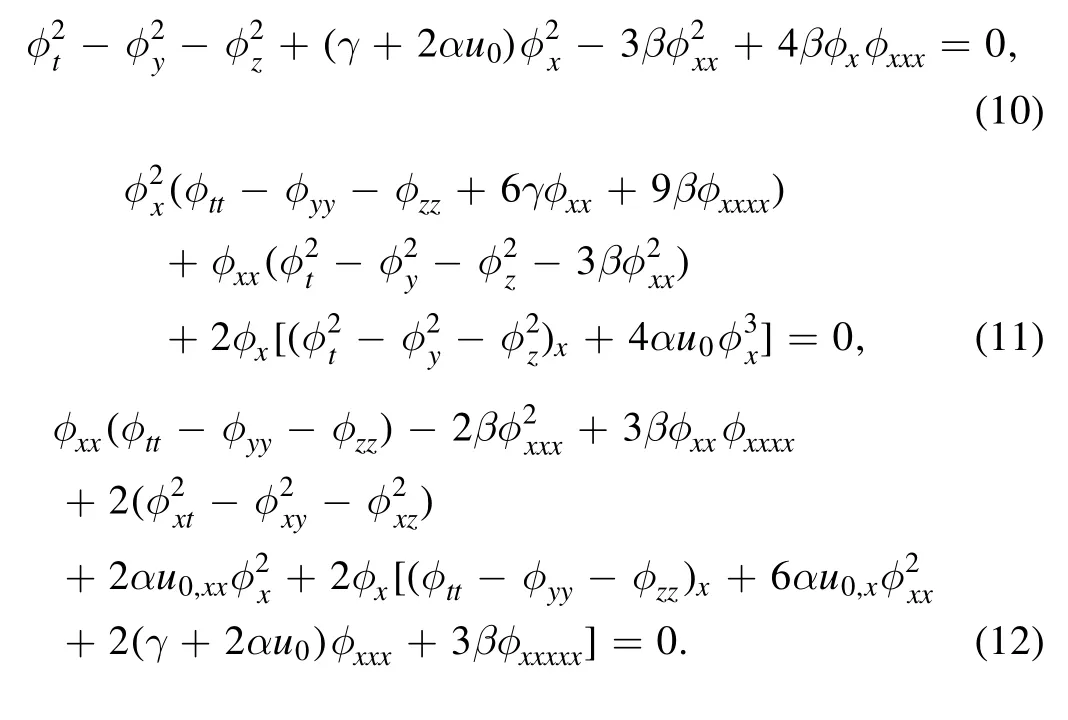
Proof.Firstly,we suppose that

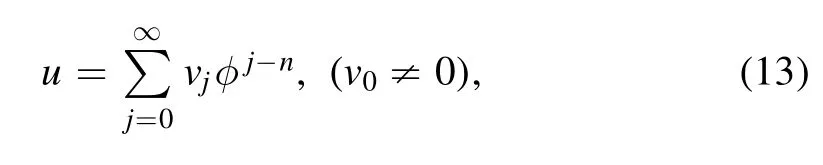
wherevj(j=0,1,2,···)are real functions ofx,y,zandtto be determined later.

Secondly,substituting equation (13) into equation (1)and analyzing the leading terms ofα(u2)xxandβuxxxxyields

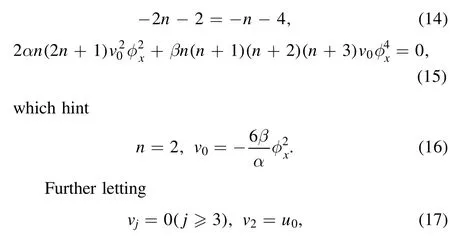
and inserting equations (13),(16) and (17) into equation (1),then setting all the coefficients of the same powers ofφs(s=-5,-4,-3,-2,-1,0)to be zeros,we have

besides equations (10)–(12).

With the help of equations (13) and (16)–(18) we finally reach equation (9).It is easy to see from equations (17) and(19) thatv2oru0is a solution of equation (1).

Theorem 3.2.The(3+1)-dimensional gB equation(1)has the following Hirota’s bilinear form:

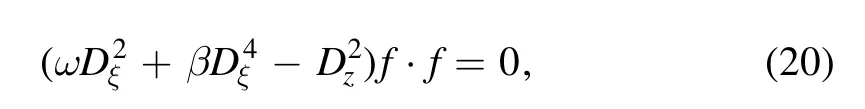
wherefis a real function ofξandz,andωandξalways represent

whereaandcare two real constants.

Proof.Obviously,equations (21) and (22) can reduce equation (1) as:

We next introduce

hereu0is assumed as a constant.Equation(1) can be written as

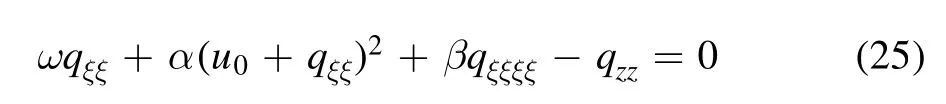
by integrating the resulting equation derived from the substitution of equation (24) into equation (1) with respect toξtwice and selecting the two integration constants as zeros.

In view of equations (9) and (24),we assume that

and substitute equation (26) into equation (25),then the following equivalent equation is derived:

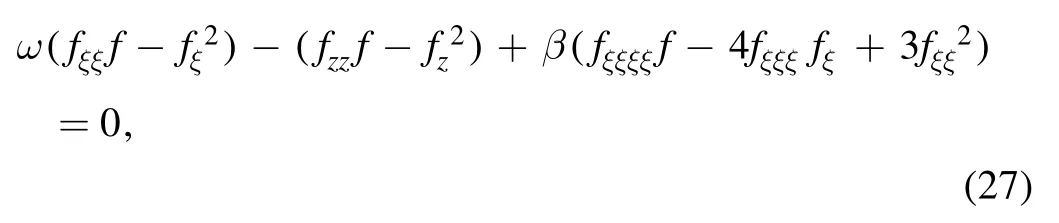
if and only ifu0=0.We finally transform equation(27)into equation (20) by Hirota’s operators (5).

4.Rogue wave solutions

Based on the bilinear form (27),we construct the first-,second-,three-and four-order rogue wave solutions of the(3+ 1)-dimensional gB equation (1).

4.1.First-order rogue wave solution

For the first-order rogue wave solution,we consider the case ofn=0 in equation (6) and select

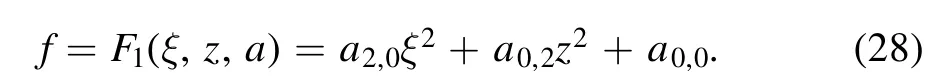
Substituting equation (28) into equation (27) and setting all the coefficients of the same powers ofzpξq(p,q=0,1,2,···)to be zeros,we get a set of polynomial equations fora2,0,a0,2anda0,0.Solving the polynomial equations,we have

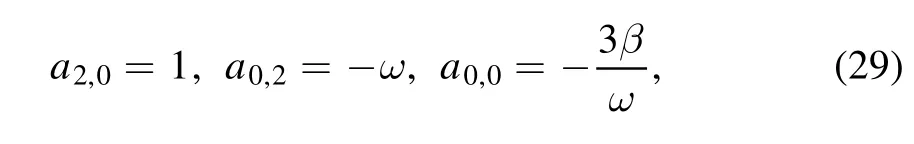
and then obtain the first-order rogue wave solution of equation (1):

Here a pair of parametersθandϑhave been embedded into equation (28) so thatfcan be taken the following form:

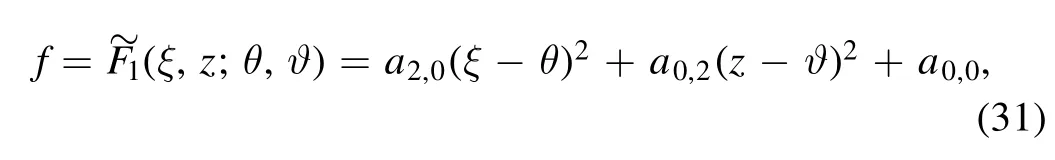
which ensures that equation(30)still solves equation(1).This is due to equations (28) and (31) having the same partial derivatives with respect toξandz.

In figure 1,the first-order rogue wave solution (30) is shown by setting

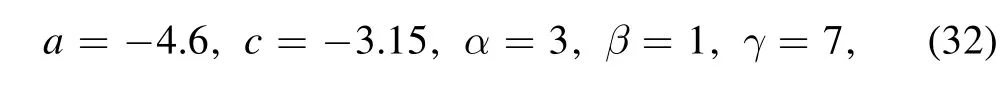
andθ=ϑ=0,respectively.At the same time,except for differentθ=ϑ=3,the selection of other parameters is the same as that in figure 1,we use figure 2 to show the first-order rogue wave solution (30).As can be seen from figures 1 and 2,the first-order rogue wave is symmetric about the linesξ=0andz=0,and its center is controlled by the parametersθandϑ.Specifically,whenθ=ϑ=0,the first-order rogue wave has the extreme value at the location(0,0),but for differentθ=ϑ=3,the extreme value appears at the point(3,3).

4.2.Second-order rogue wave solution

For the second-order rogue wave solution,we consider equation (6) whenn=1,that is

Substituting equation (33) into equation (27) and setting all the coefficients of the same powers ofzpξq(p,q=0,1,2,···)to be zeros,we get a set of polynomial equations fora6,0,a4,2,a4,0,a2,4,a2,2,a2,0,a0,6,a0,4,a0,2,a0,0,b2,0,b0,2,b0,0,c2,0,c0,2andc0,0.Solving the polynomial equations,we gain

and therefore obtain the second-order rogue wave solution of equation (1):

In figures 3 and 4,we show the second-order rogue wave solution (39).It can be seen from figure 3 that whenθ=ϑ=0the second-order rogue wave has two interaction wave peaks.However,with the increase ofθandϑ,the computer simulation shows that these two interaction wave peaks gradually separate and give birth to the third wave peak.For the case ofθ=ϑ=200,figure 4 shows the second-order rogue wave with three separated wave peaks.In addition,we can see that the second-order rogue wave in figure 3 is symmetric with respect to the linesξ=0 andz=0,but the one in figure 4 is asymmetric.

4.3.Third-order rogue wave solution

For the third-order rogue wave solution,we consider equation (6) withn=2:

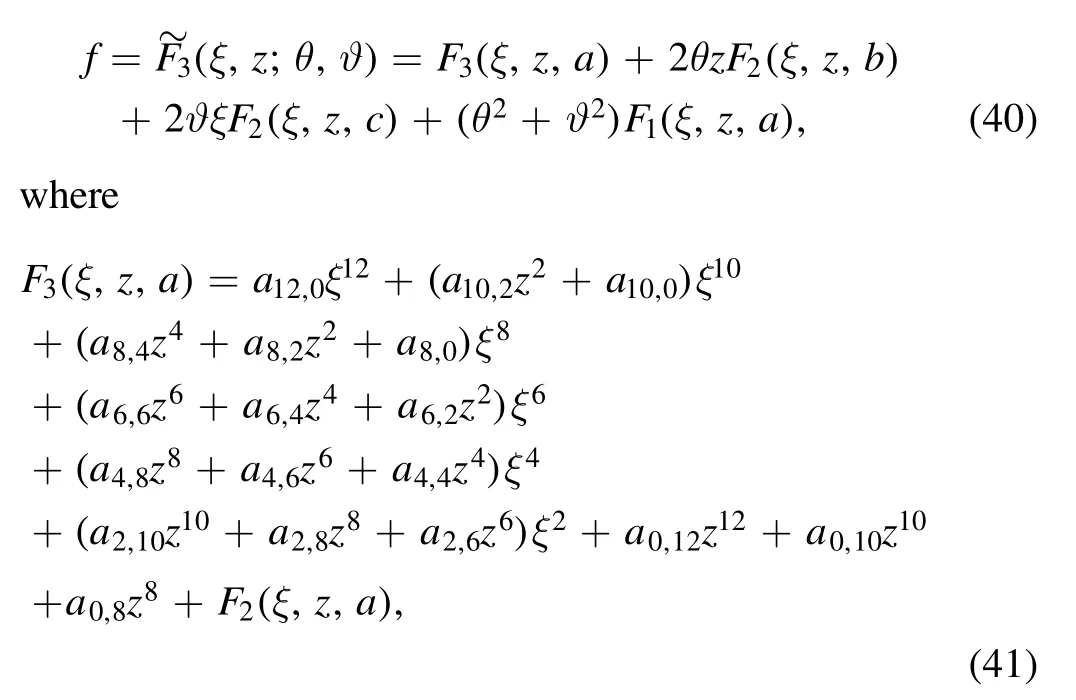
Figure 1.First-order rogue wave localized in (30) with a=-4.6,c=-3.15,α=3,β=1,γ=7,ϑ=0andθ=0,(a) 3D graph;(b)contour plot;(c) profile at z=0.

Substituting equation (40) into equation (27) and setting all the coefficients of the same powers ofzpξq(p,q=0,1,2,···)to be zeros,we get a set of polynomial equations for the undetermined constants in equations (35),(41) and (42),from which we have

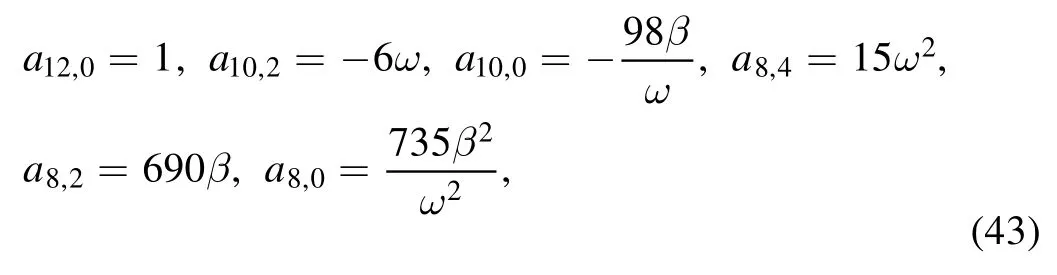
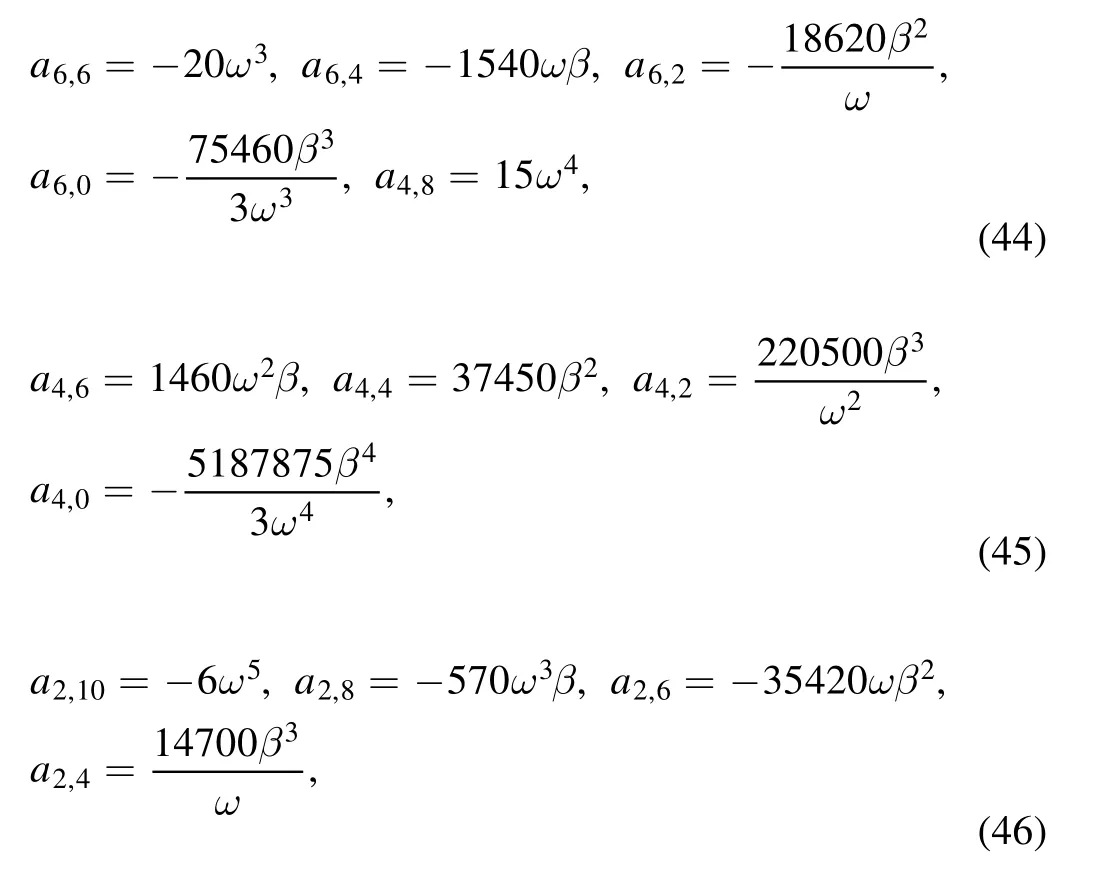
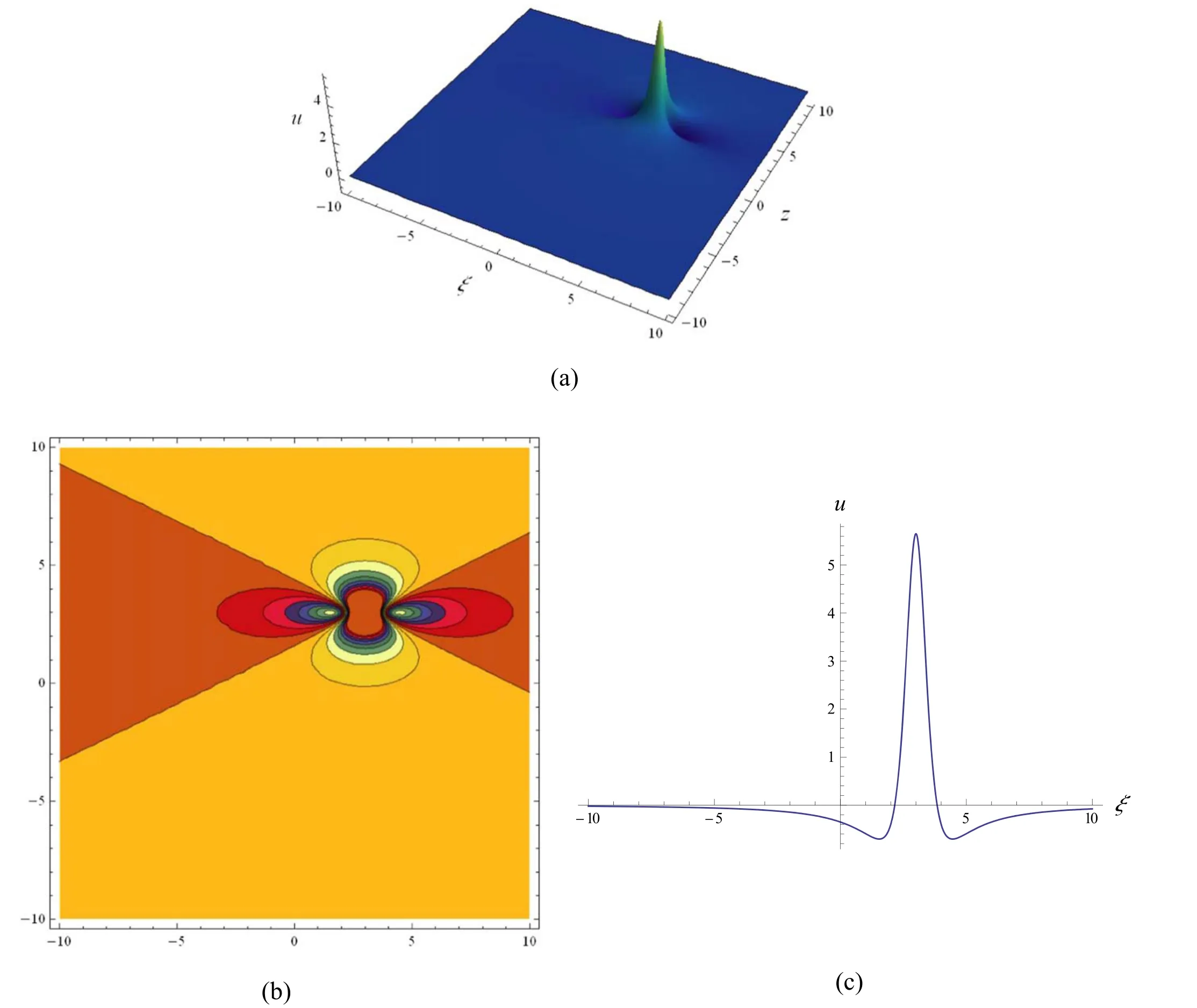
Figure 2.First-order rogue wave localized in (30) with a=-4.6,c=-3.15,α=3,β=1,γ=7,ϑ=3andθ=3,(a) 3D graph;(b)contour plot;(c) profile at z=3.

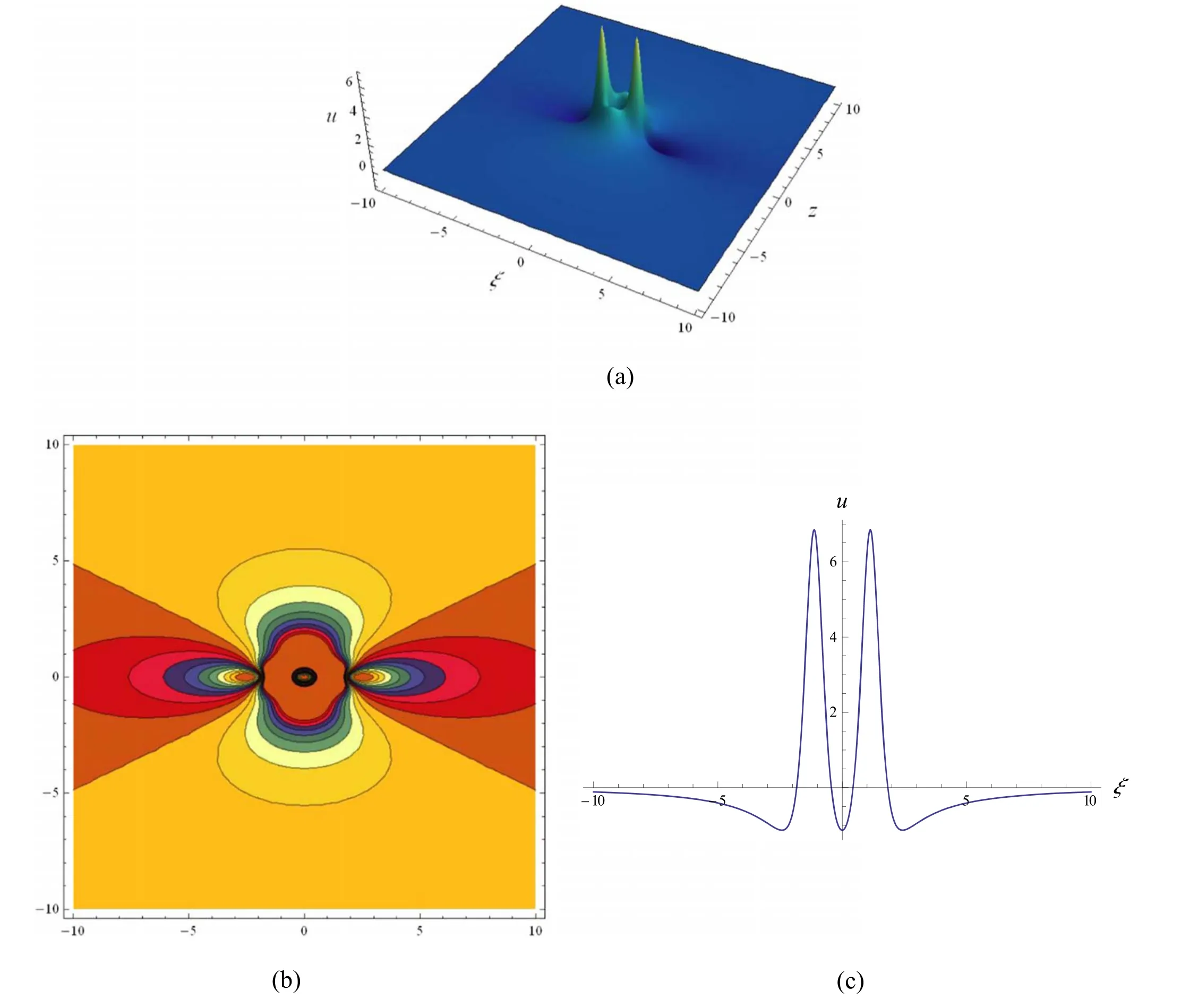
Figure 3.Second-order rogue wave localized in(39)with a=-4.6,c=-3.15,α=3,β=1,γ=7,ϑ=0andθ=0,(a)3D graph;(b)contour plot;(c) profile at z=0.

and therefore obtain the third-order rogue wave solution of equation (1):

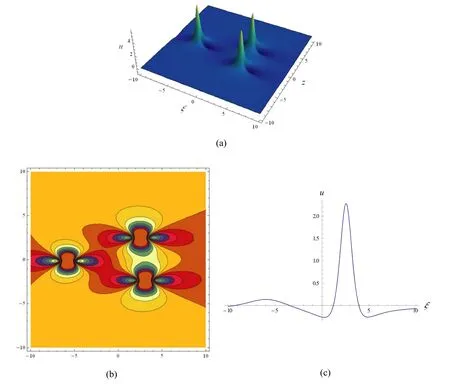
Figure 4.Second-order rogue wave localized in(39)with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=200and ϑ=200,(a)3D graph;(b) contour plot;(c) profile at z=2.

In figure 5,we show the third-order rogue wave solution(55)with three interaction wave peaks,which is symmetric with respect to the linesξ=0 andz=0.The highest wave peak is located at the center(0,0),and the other two entangled second highest wave peaks surround the center.Similar to the secondorder rogue wave in figure 3,the three interaction wave peaks in figure 5 gradually separate and give birth to another three wave peaks as long as one or all ofθandϑis/are given sufficiently large value(s).When eitherθorϑis equal to zero,we show the third-order rogue wave solution (55) that is symmetric with respect to the linesξ=0 andz=0 in figures 6 and 7,respectively.That is to say thatθ=0 makes the third-order rogue wave symmetric with respect to the lineξ=0,whileϑ=0makes the third-order rogue wave symmetric with respect to the linez=0.However,for the non-zerosθandϑ,the thirdorder rogue wave is asymmetric,see figure 8 for example.

4.4.Fourth-order rogue wave solutions

For the fourth-order rogue wave solution,we consider equation (6) withn=3:

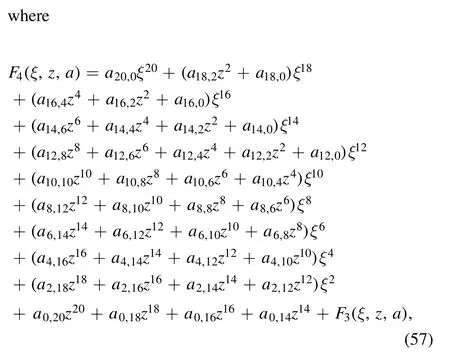
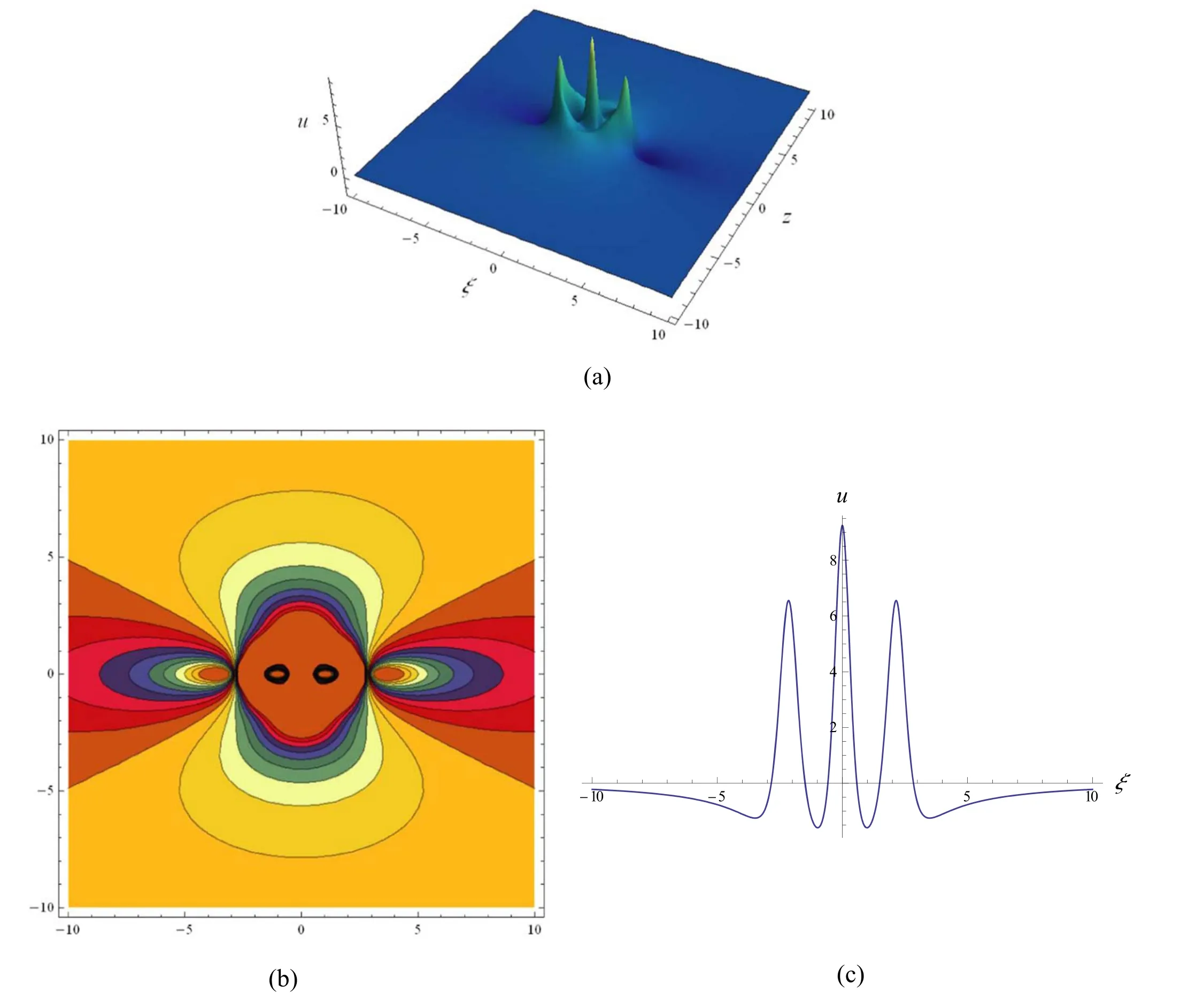
Figure 5.Third-order rogue wave localized in (55) with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=0andϑ=0,(a) 3D graph;(b)contour plot;(c) profile at z=0.

andF3(ξ,z,a),F3(ξ,z,b)andF3(ξ,z,c)are determined by:

Substituting equation (56) into equation (27) and setting all the coefficients of the same powers ofzpξq(p,q=0,1,2,···)to be zeros,we get a set of polynomial equations,and from which the undetermined constants can be determined as follows:

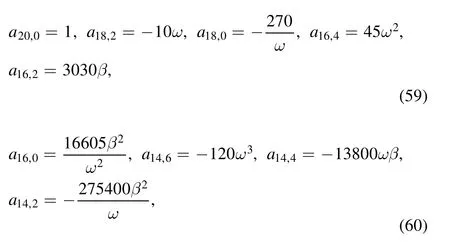
Figure 6.Third-order rogue wave localized in(55)with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=0and ϑ=2000,(a)3D graph;(b)contour plot;(c) profile plot at z=0.

Figure 7.Third-order rogue wave localized in(55)with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=0and ϑ=9 ×10 4,(a)3D graph;(b) contour plot;(c) profile at z=0.

Figure 8.Third-order rogue wave localized in(55)with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=600and ϑ=600,(a)3D graph;(b) contour plot;(c) profile atξ=0.

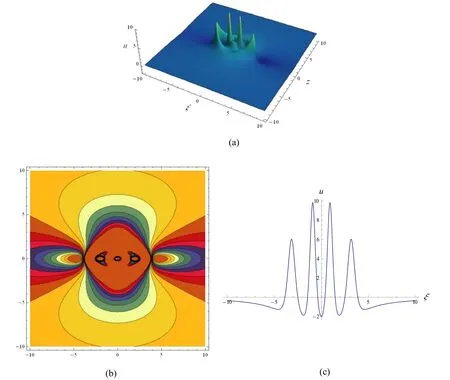
Figure 9.Fourth-order rogue wave localized in(97)with a=-4.6,c=-3.15,α=3,β=1,γ=7,ϑ=0andθ=0,(a)3D graph;(b)contour plot;(c) profile at z=0.

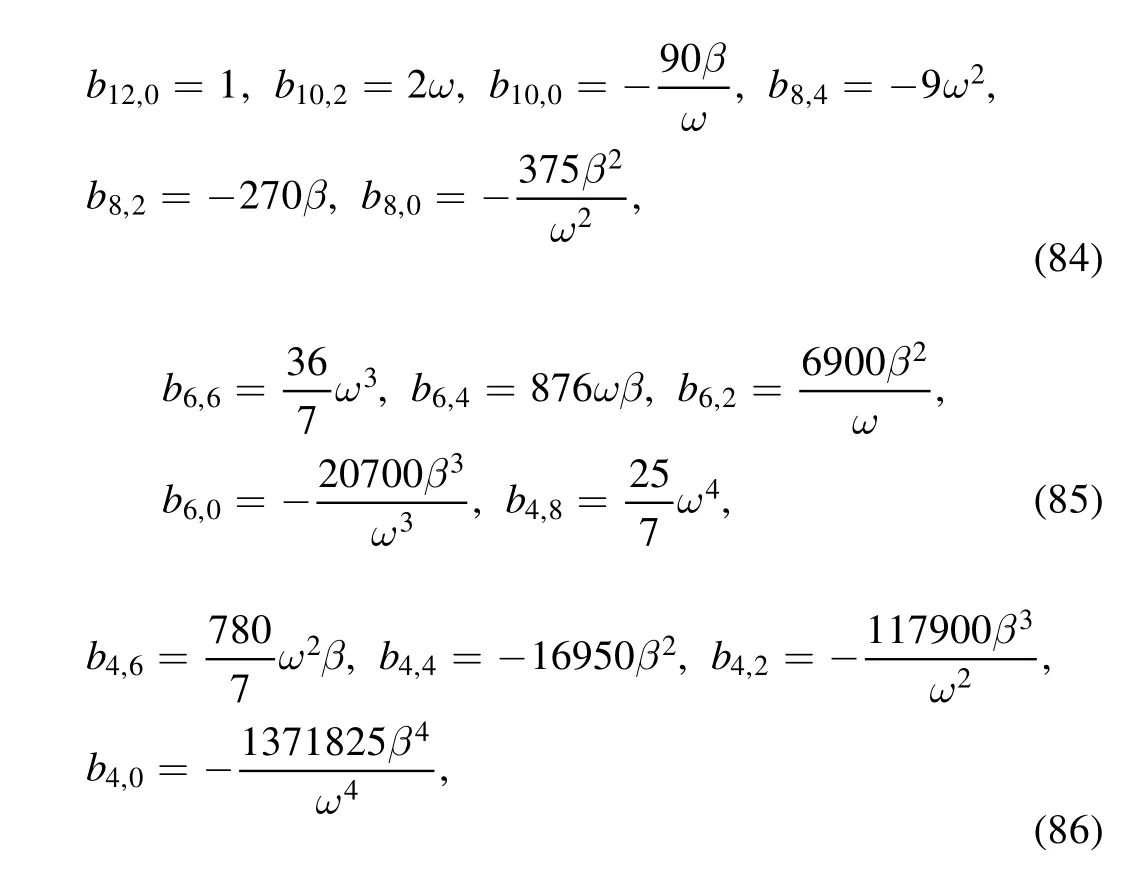
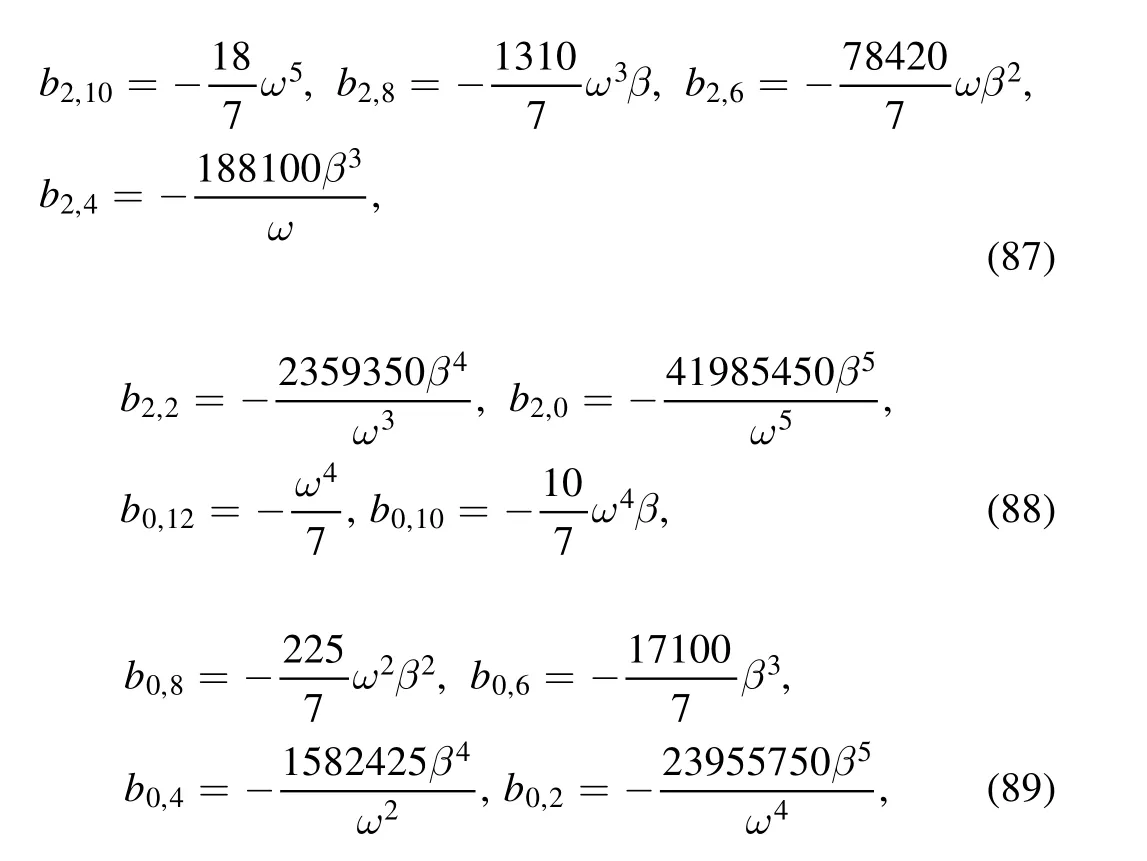
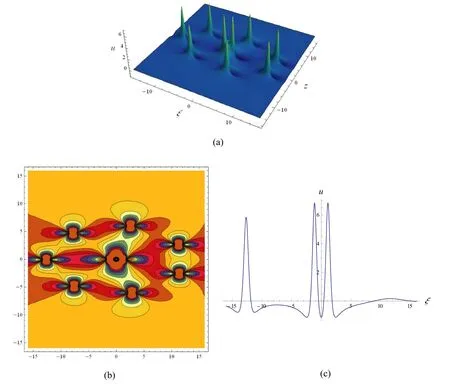
Figure 10.Fourth-order rogue wave localized in (97) with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=0and ϑ=6 ×107,(a) 3D graph;(b) contour plot;(c) profile at z=0.

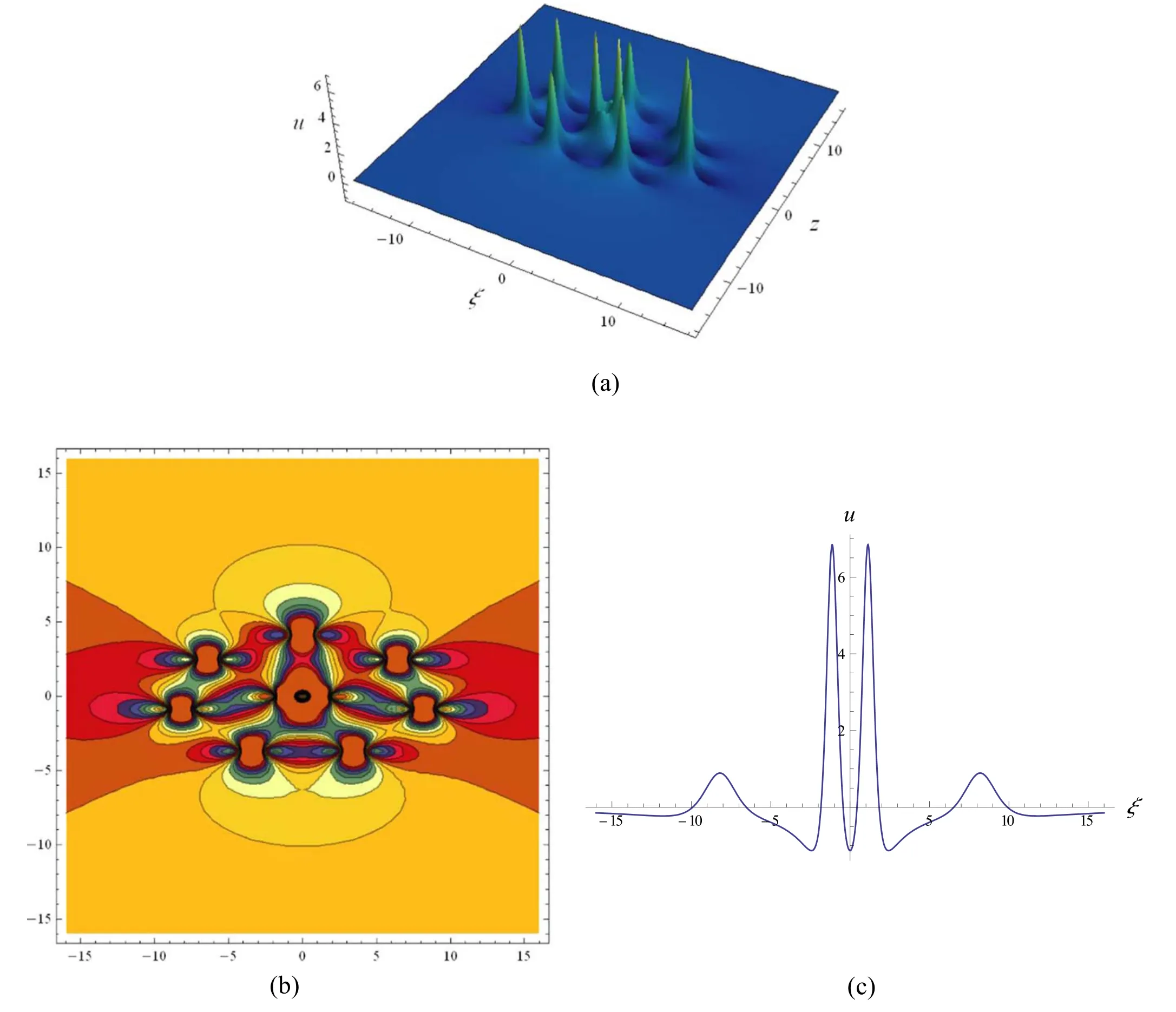
Figure 11.Fourth-order rogue wave localized in (97) with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=6 ×107andϑ=0,(a) 3D graph;(b) contour plot;(c) profile at z=0.

We,therefore,obtain the fourth-order rogue wave solution of equation (1):

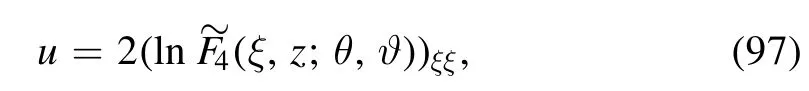
Similarly,we show in figure 9 the fourth-order rogue wave solution (97) with four interaction wave peaks.The highest two peaks are located at the center(0,0),and the other entangled second highest wave peaks surround the center.Similar to the second-and third-order rogue waves in figures 3 and 5,the four interaction wave peaks in figure 9 gradually separate and give birth to another five wave peaks as long as one or all ofθandϑis/are given sufficiently large value(s).For example,see figures 10 and 11 for two symmetric fourth-order rogue waves,the one corresponding toθ=0andϑ=6 ×107is symmetric with respect to the linez=0,and the other givenθ=6 ×107andϑ=0is symmetric with respect to the lineξ=0.However,the parametersθ=6 ×107andϑ=6 ×107lead to an asymmetric fourth-order rogue wave,see figure 12.

5.Conclusion and discussion

In summary,we have constructed first-,second-,third-and fourth-order rogue wave solutions(30),(39),(55)and(97)of the (3+1)-dimensional gB equation (1) through Zhaqilao’s symbolic calculation approach [22].To the best of our knowledge,the high-order rogue wave solutions (39),(55)and(97)are new.This paper shows that the two parametersθandϑincluded in solutions (30),(39),(55) and (97) control the following aspects:

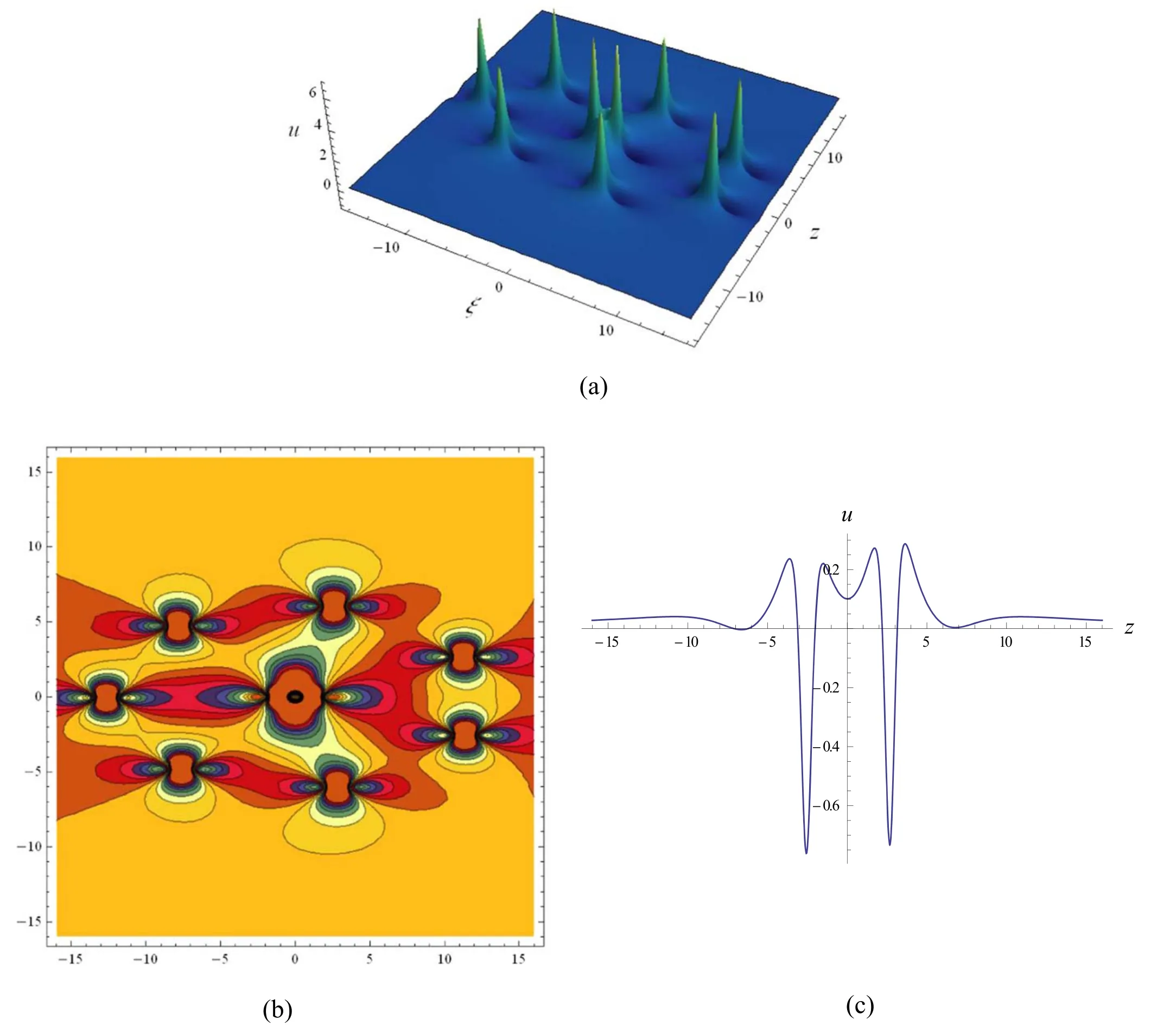
Figure 12.Fourth-order rogue wave localized in(97)with a=-4.6,c=-3.15,α=3,β=1,γ=7,θ=6 ×107and ϑ=6 ×107,(a)3D graph;(b) contour plot;(c) profile atξ=10.

(1) The center(θ,ϑ) of the first-order rogue wave solution (30).

(2) The fission giving birth to more wave peaks of the second-,third-and fourth-order rogue wave solutions(39),(55) and (97),the larger the value ofθandϑ,the larger the distance between the wave peaks

(3) The symmetry of high-order rogue wave solutions (39),(55)and(97),the rules of which are that when one or all ofθandϑare zero(s)then these rogue wave solutions are symmetric with respect to the linez=0 whenθ=0 or the lineξ=0 whenϑ=0,but asymmetric forθϑ≠0.

In view of the controllability of parametersθandϑon the center,fission and asymmetry of first-,second-,third-and fourth-order rogue wave solutions (30),(39),(55) and (97),we can consider their potential applications in physics,such as the design of adjustable resistors and controllable switching devices under specific environment or with special requirements.Since the gB equation (1) or its reduced equation (23) is a kind of fluid equation,if the fluid is assumed to be a conductive liquid,we can not only use the vibration of the wave peak to trigger the connected power supply,but also adjust the size of the resistance by adjusting the number of fission wave peaks,so as to achieve the purpose of designing adjustable resistance and controllable switching device.If feasible,we can also consider using the controllability of wave crest position and asymmetry of rogue wave solutions (30),(39),(55) and (97) to design adjustable resistors and controllable switching devices that meet other conditions including the horizontal position and vertical height design of the device electric shock point.Nonetheless,we are still looking forward to other physical applications of these obtained rogue wave solutions with controllable center,fission and asymmetry.

For the method [22],it is a novel and meaningful discovery that the fission and asymmetry of higher-order rouge waves can be controlled by the embedded parametersθand.ϑHigh asymmetry is an important observation point in the study of rogue waves.Although the rogue wave solutions obtained in this paper have asymmetric controllability,there is still a certain distance from the highly asymmetric rogue waves,which raises a problem worthy of study for our next work.Nonlinear problems are always full of infinite charm and challenges.Some meaningful developments of nonlinear models deserve attention,such as theH2optimal controller of coupled stochastic algebraic Riccati equations [32],and the influence of higher-order nonlinear effects on optical solitons [33].

Acknowledgments

We would like to thank the Editor and three anonymous referees for the helpful comments.This work was supported by Liaoning BaiQianWan Talents Program of China(LRS2020[78]),the Natural Science Foundation of Education Department of Liaoning Province of China (LJ2020002) and the National Natural Science Foundation of China(11547005).