Multi-solutions with specific geometrical wave structures to a nonlinear evolution equation in the presence of the linear superposition principle
2023-02-16HajarIsmaelTukurAbdulkadirSulaimanandOsman
Hajar F Ismael,Tukur Abdulkadir Sulaimanand M S Osman
1 Department of Mathematics,Faculty of Science,University of Zakho,Zakho,Iraq
2 Department of Computer Engineering,Biruni University,Istanbul,Turkey
3 Department of Mathematics,Faculty of Science,Cairo University,Giza 12613,Egypt
Abstract Lump solutions are one of the most common solutions for nonlinear evolution equations.This study aspires to investigate the generalized Hietarintatype equation.We auspiciously provide multiple M-lump waves.On the other hand,collision phenomena to multiple M-lump waves with soliton wave solutions are also provided.During the collision,the amplitude of the lump will change significantly over the processes,whereas the amplitude of the soliton will just minimally alter.As it is of paramount importance,we use suitable values of parameter to put out the physical features of the reported results through three dimensional and contour graphics.The results presented express physical features of lump and lump interaction phenomena of different kinds of nonlinear physical processes.Further,this study serves to enrich nonlinear dynamics and provide insight into how nonlinear waves propagate.
Keywords: the generalized Hietarintatype equation,M-lump waves,interaction phenomena,hirota bilinear method
1.Introduction
A wave is a dynamic disturbance of one or more quantities that propagates and is frequently expressed by a wave equation in physics,mathematics,and related subjects.At least two field quantities are present in the wave medium for physical waves.When quantities oscillate at a set frequency around an equilibrium value,periodic waves are provided.A standing wave is provided when two superimposed periodic waves travel in opposite directions.A traveling wave is provided when the entire waveform travels in one direction.When the wave amplitude appears to be resized or even nil,a standing wave’s vibrational amplitude nulls out at certain points.In mathematics and physics,a soliton,also known as a solitary wave,is a wave packet that keeps its structure while travelling at a constant speed.When dispersive and nonlinear effects in a medium balance out,soliton formation arises.A class of weakly nonlinear dispersive partial differential equations has physical system solutions called solitons[1–6].
Partial differential equations are usually utilized in scientific areas with a powerful quantitative focus.such as physics and engineering.For instance,general relativity,quantum mechanics,electrostatics,electrodynamics,thermodynamics,fluid dynamics,elasticity,and many more areas are all founded on them.The Poincaré conjecture from geometric topology is one of their most notable applications,although they also come from purely mathematical ideas like differential geometry and the calculus of variations [7,8].
In addition,several studies show that interaction solutions between lumps and other types of solutions to nonlinear integrable equations existed.It should be emphasized,however,that numerous approaches such as the Lie symmetric analysis and its application[9–14],the Kudryashov method[15,16],the tanhcoth method[17],the improved Sardar-subequation[18],the new generalized auxiliary equation method[19],and other techniques[20–24] have been employed for generating interaction phenomena for nonlinear differential equations.Values are assigned to these constant coefficients in particular conditions to ensure that solutions exist [25–41].Nonetheless,it is worth emphasizing that the problem of dealing with such interactions has yet to be studied.This article provides us with lump collision phenomena to the generalized Hietarintatype equation[42]
The multi-soliton solutions,one-lump wave,and mixed onelump-soliton wave have been studied in [42].It is worth noting that when α2=0 and γ1=0,the aforementioned equation is simplified to the following equation:

In this work,we are interested to study multiple M-lump waves.and constructing interactions of M-lump waves with soliton wave solutions.These interesting solutions are original and have not been proposed in other research papers.
The introduction and primary problem are covered in the first section of the paper.The sorts of M-lump wave solutions are addressed using the long-wave technique in the second section.The third section introduces the phenomenon of collision between 1-and 2-M-lump wave solutions and 1-or 2-soliton solutions.Breather wave,mixed breather-soliton,and mixed breather-M-lump waves are all examined in the fourth section.In the final section,conclusions are made.
2.M-lump wave solutions
Consider equation (2).With the transformation
It is easy to know that whenfsolves equation (2) thenuis a solution of equation (1).Usually,the soliton results are provided by utilizing
∑μ=0,1stands for a summation that comprises of all possible gatherings of μi=0,1,fori=1,2,K,N.Substituting(2)into equation (1) and integrating it with respect toxprovides
The Hirota bilinear form of equation (5) becomes

whereDis the Hirota bilinear operator,and provided by Hirota direct method as
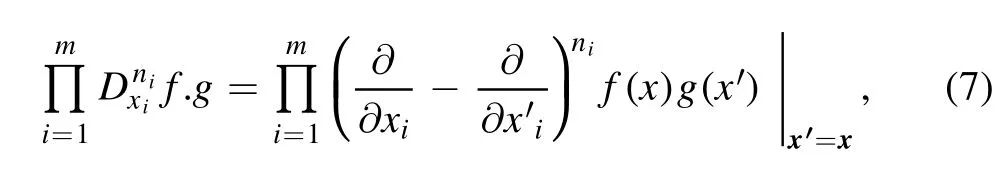
wherex=(x1,x2,…,x M),x′=(x′1,x′2,…,x′M)are vectors andn1,n2,K,nMare random non-negative integers numbers.Let the dispersion variable Φmis defined as

where the dispersion relation and the phase shift are

TakingN=1 in equation (3) and put it into equation (2),we get an equation that presents a one-soliton solution
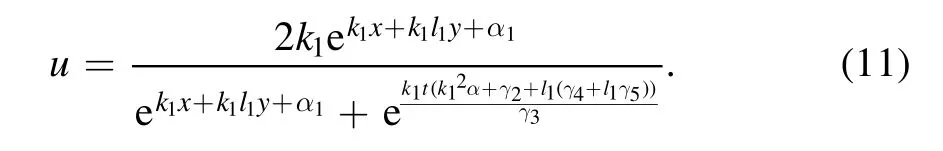
UtilizingN=2 in equation (3),provides
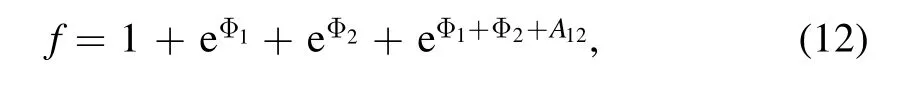
where eAijis defined in equation(9).As a result of substituting equations(11)into(2),we obtain an equation that describes a two-soliton solution.Also,by takingN=3 in equation (3),a result is

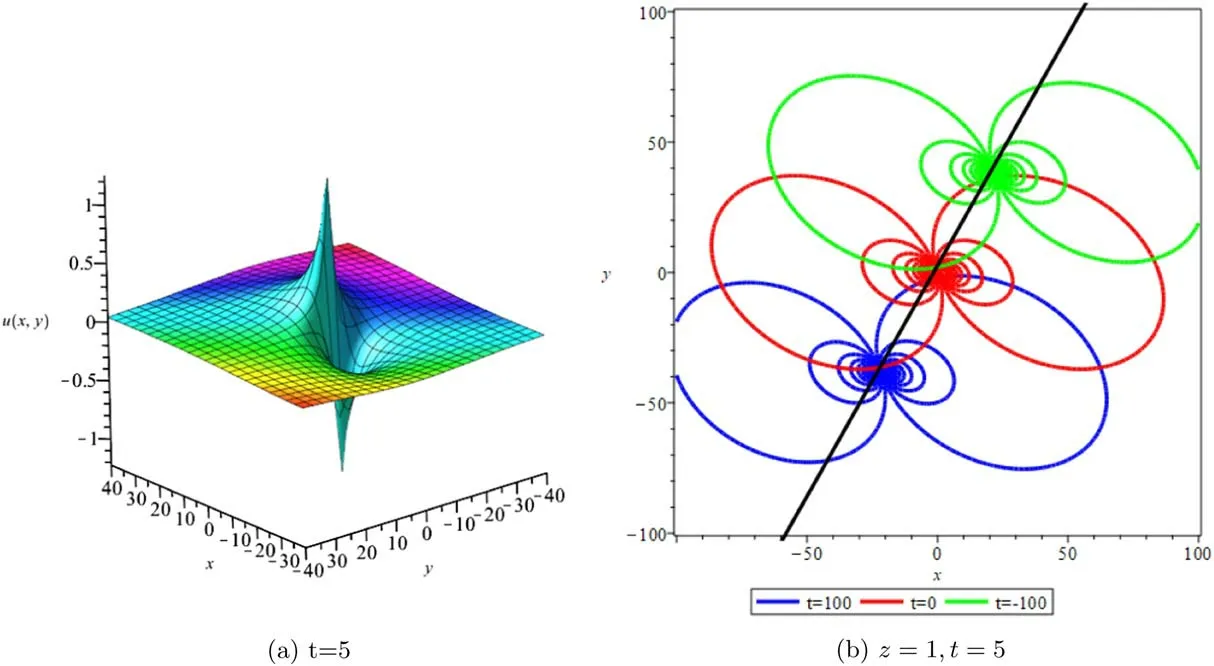
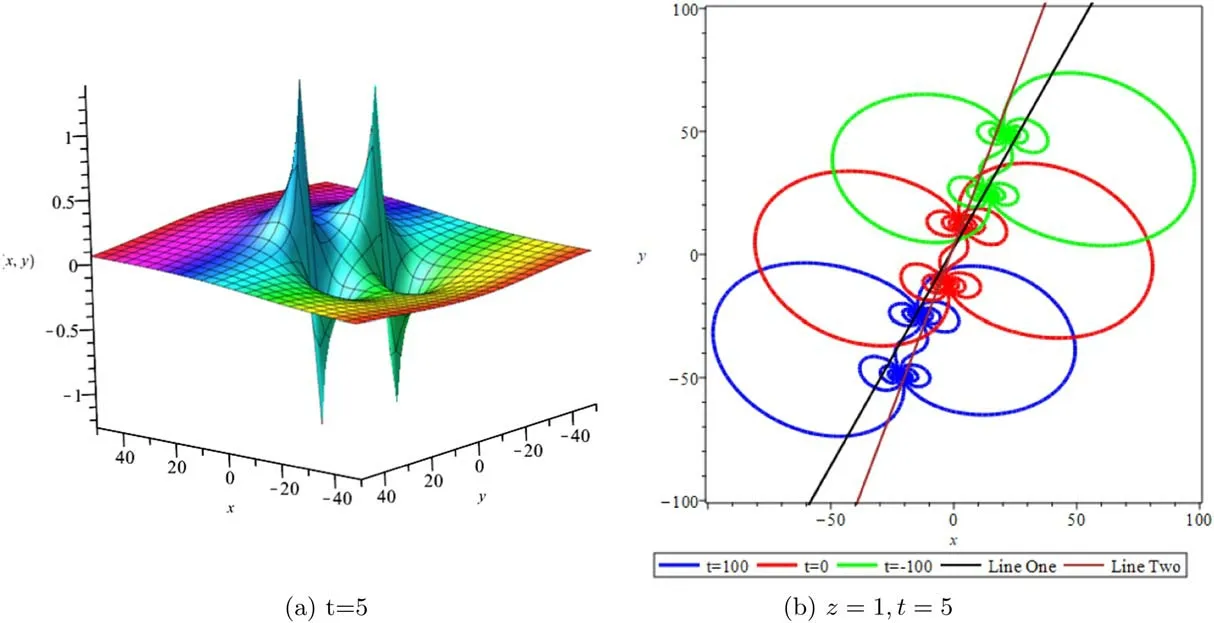
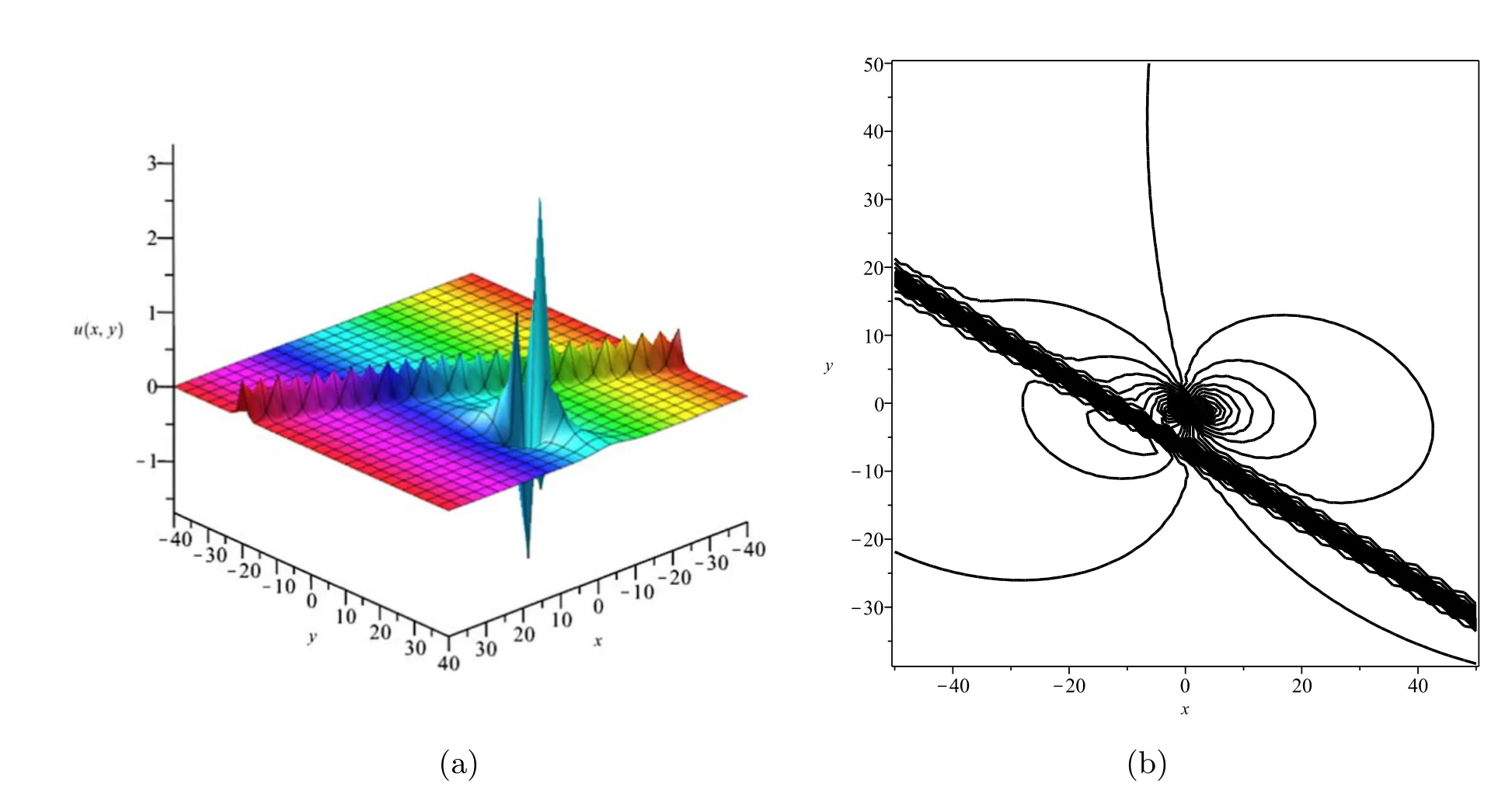
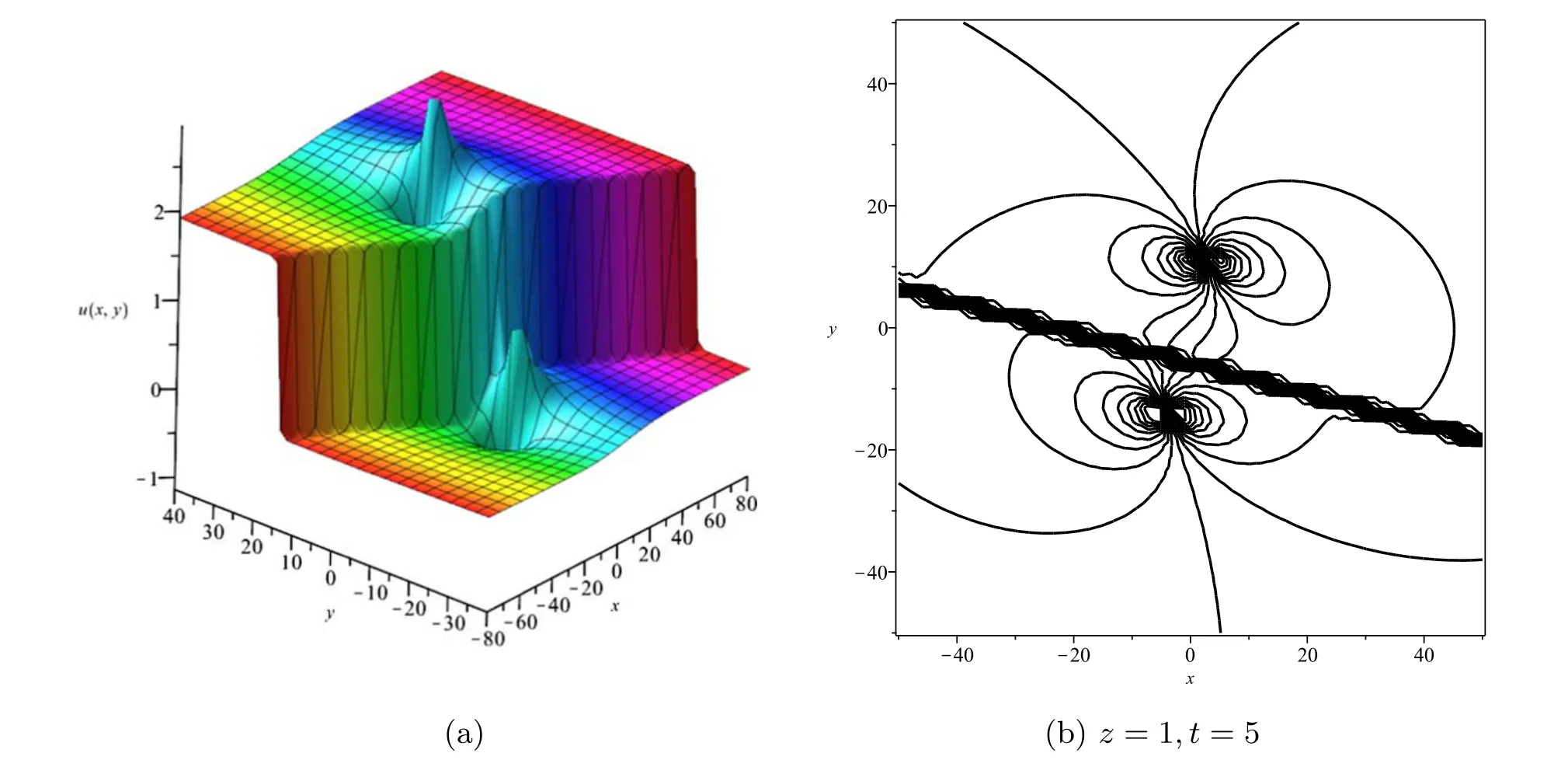
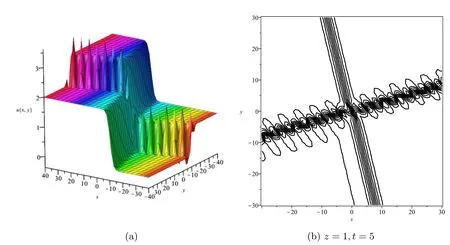
whereA123=A12A13A23andAij(i We now provide M-lump waves of the studied equation,using the long-wave method.Pluggingeα=-1iinto equations (7),(3) holds the formula Insertingki→0 intofN,provides Figure 1.Multiple soliton wave when γ2=1/2,γ3=-1,γ4=1/4,γ5=1/5,α=-1/5, t=2. Inserting equations (13)–(15) into (2),provides With a single-M-lump wave for equation (2) as shown in figure 2.This rational result is a permanent wave result decomposing asand travelling with the speed Finding out that this wave travels in the following straight line is interesting A one-M-lump wave that travels along this line at different times is drawn in figure 1(b). To derive a 2-M-lump result to equation(2),we letN=4 in equation (3),and considering eαi=-1(i=1,2,3,4),ki→0,we provide where Θ1,Θ2,Θ3,Θ4,wi,Bij(i Inserting equations (17) into (3),provides The travel of two-M-lump waves alongside the two lines is graphed in figure 3 in different periods. To provide a 3M-lump result of equation (1),we implementki→0,eαi=-1,(i=1,2,3,4,5,6)and considerN=6 in equation (3),which provides We should know that Θ1,Θ2,Θ3,Θ4,Θ5,Θ6,Bijandare provides in equations (14) and (15),respectively.Subsequently,inserting equations(21)into(3),a 3-M-lump result is provided as displayed in figure 4.We should know thatl1=a1+ib1,l2=a2+ib2,l3=a3+ib3,l4=l1*,l5=l2*andl6=l3*.The following straight lines are followed by a three-M-lump wave,which is interesting to know In figure 5,the three-M-lump waves’ path along these three lines is graphed for various times. Figure 2.One-M-lump wave when a1=1/3, b1=8/7,γ2=1/2,γ3=-1,γ4=1/4,γ5=1/5,α=-1/5. Figure 3.Two-M-lump wave when a1=1/3, b1=8/7, a2=1/4, b2=4/3,γ2=1/2,γ3=-1,γ4=1/4,γ5=1/5,α=-1/5. This section attempts to design the collision of a 1-M-lump result along with one-soliton,two-soliton,and a 2-M-lump wave with a single soliton.To begin with,we setN=3 in equation (3) and take the limitki→0,(i=1,2)and,and this provides Here Φ3is expressed in equation (7),Θi(i=1,2)are provided in equation (14),B12is given in equation (15).C13,C23are derived as follows A result that depicts the interaction between a 1-M-lump solution and a 1-soliton solution is obtained by putting equations(20)into(19),and then into equation(3),as shown in figure 4. To provide a collision of two-soliton with an M-lump wave,we consider that Figure 4.Three-M-lump wave when a1=1/3,b1=8/7,a2=1/4,b2=9/7,a3=1/5,b3=10/7,γ2=1/2,γ3=-1,γ4=1/4,γ5=1/5,α=-1/5. Figure 5.Mixed M-lump-soliton wave when a1=1/3, b1=3/2, k3=1, l3=2,α3=5,γ2=1/2,γ3=-1,γ4=1/4,γ5=1/5,α=-1/5, t=5. The constantsBijandCijare provided in equations (14) and(20).The functions Φiand Θiare provided in equations (7)and (15).Inserting equations (21) into (2),an outcome is a result that stands for a collision between a one-M-lump wave and a two-soliton solution which display in figure 6. Figure 6.Mixed M-lump-two-soliton wave when a1=1/3,b1=3/2,a2=1/4,b2=9/7,k3=1,l3=2,k4=3/4,l4=1,α3=10,α4=0,γ2=1/2,γ3=-1,γ4=1/4,γ5=1/5,α=-1/5, t=5. Figure 7.Mixed two-M-lump-soliton wave when a1=1/3, b1=8/7, a2=1/4, b2=4/3, k5=1, l5=4,α5=1,γ2=1/2,γ3=-1,γ4=1/4,γ5=1/5,α=-1/5, t=5. WhenN=5 and considering the limitki→0,(i=1,2,3,4)in equation (3),the collision between two-M-lump wave and one-soliton are In this article,all constants and functions are listed.Now that we have provided a collision between a two-M-lump and a one-soliton solution,inserting equations(22)into(3),and the consequence is the aspect displayed in figure 7. In this section,we try to explore some new solutions to the suggested equation like breather wave,mixed breathersoliton,and mixed breather-M-lump waves.Takingin equation (10)then into equation (2) a result yields a breather wave as presented in figure 8. Figure 8.Breather wave when α1=0,α2=0,γ2=1/2,γ3=-1,γ4=1/4,γ52=1/5,α=-1/5, t=2. Figure 9.Mixed breather-soliton wave when k3=1, l3=1/4,α1=0,α2=0,α3=0,γ2=1/2,γ3=-1,γ4=1/4,γ52=1/5,α=-1/5, t=2. An interaction physical phenomena between breather and soliton solution could be constructed by takingin equation (12) then substituting these values into equation(2),an outcome gives us a mixed breather-soliton wave as seen in figure 9. Moreover,to offer a mixed breather-M-lump wave,we letin equation(21)and putting these values into equation(2)gives an interaction between the breather wave and M-lump wave as shown in figure 10. This study investigated the generalized Hietarintatype equation.Multiple M-lump waves alongside their collision phenomena to multiple M-lump waves with soliton wave solutions are auspiciously provided.Using suitable values of parameter,we put out the physical features of the reported results through three dimensional and contour graphics.The results presented express physical features of lump and lump interaction phenomena of different kinds of nonlinear physical processes.Further,Breather solutions and their interactions such as breather waves,mixed breather-solitons,and mixed breather-M-lump waves have been investigated.In a subsequent paper,we analyze the extended Hietarintatype equation with variable coefficients and derive a number of novel conclusions for this model. Figure 10.Mixed breather-M-lump wave when a1=1/3, b1=10/7, a2=1/4, b2=13/7,α3=0,α4=0,γ2=1/2,γ3=-1,γ4=1/4,γ52=1/5,α=-1/5, t=2. Conflict of interest The authors declare that they have no conflict of interest. Ethical standard The author state that this research paper complies with ethical standards.This research paper does not involve either human participants or animals. ORCID iDs
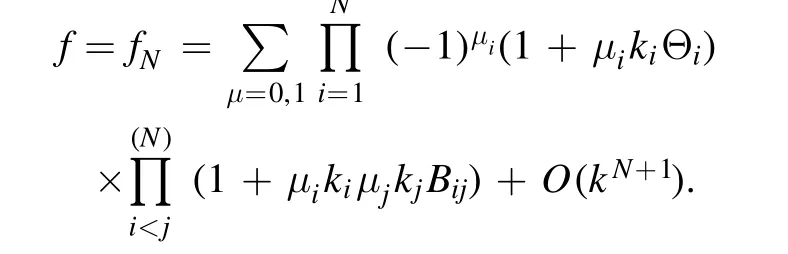

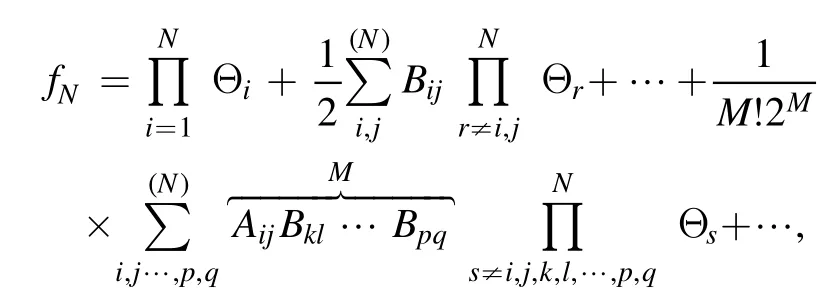

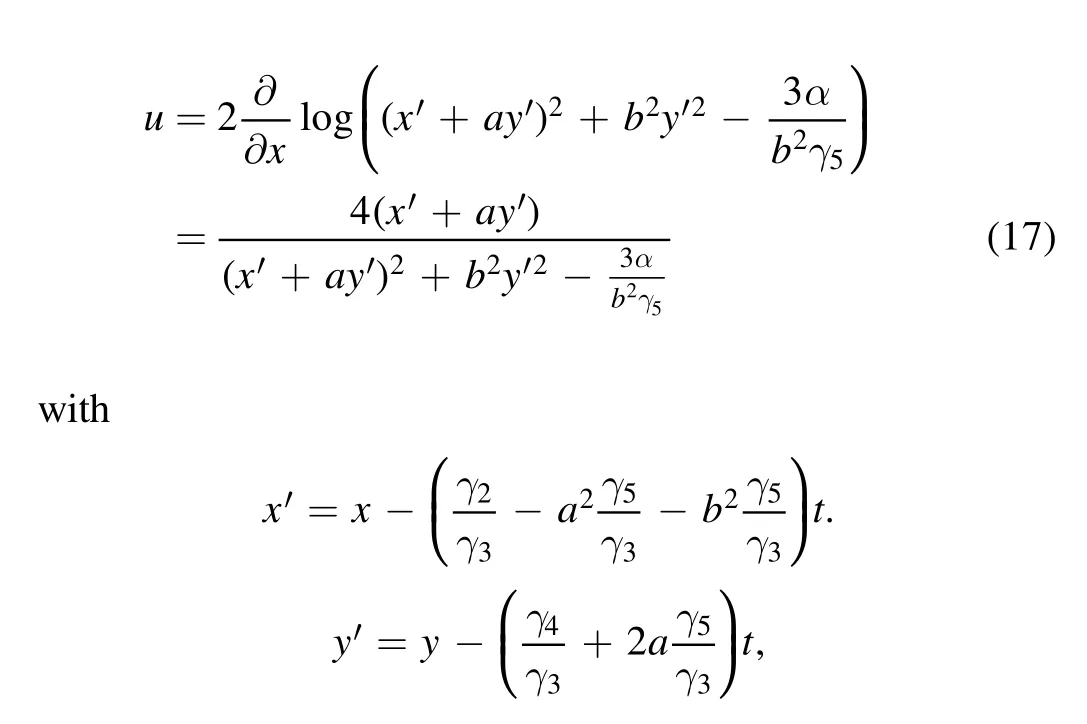

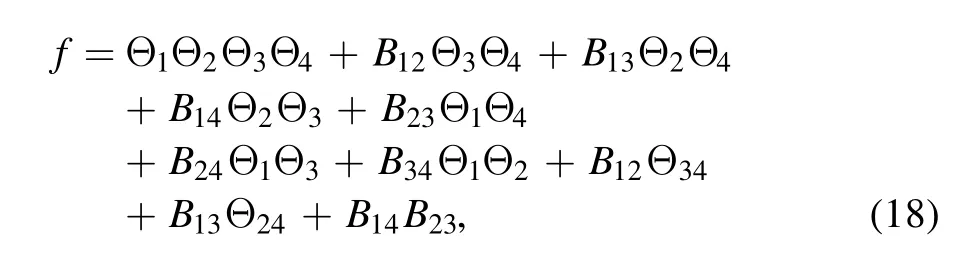

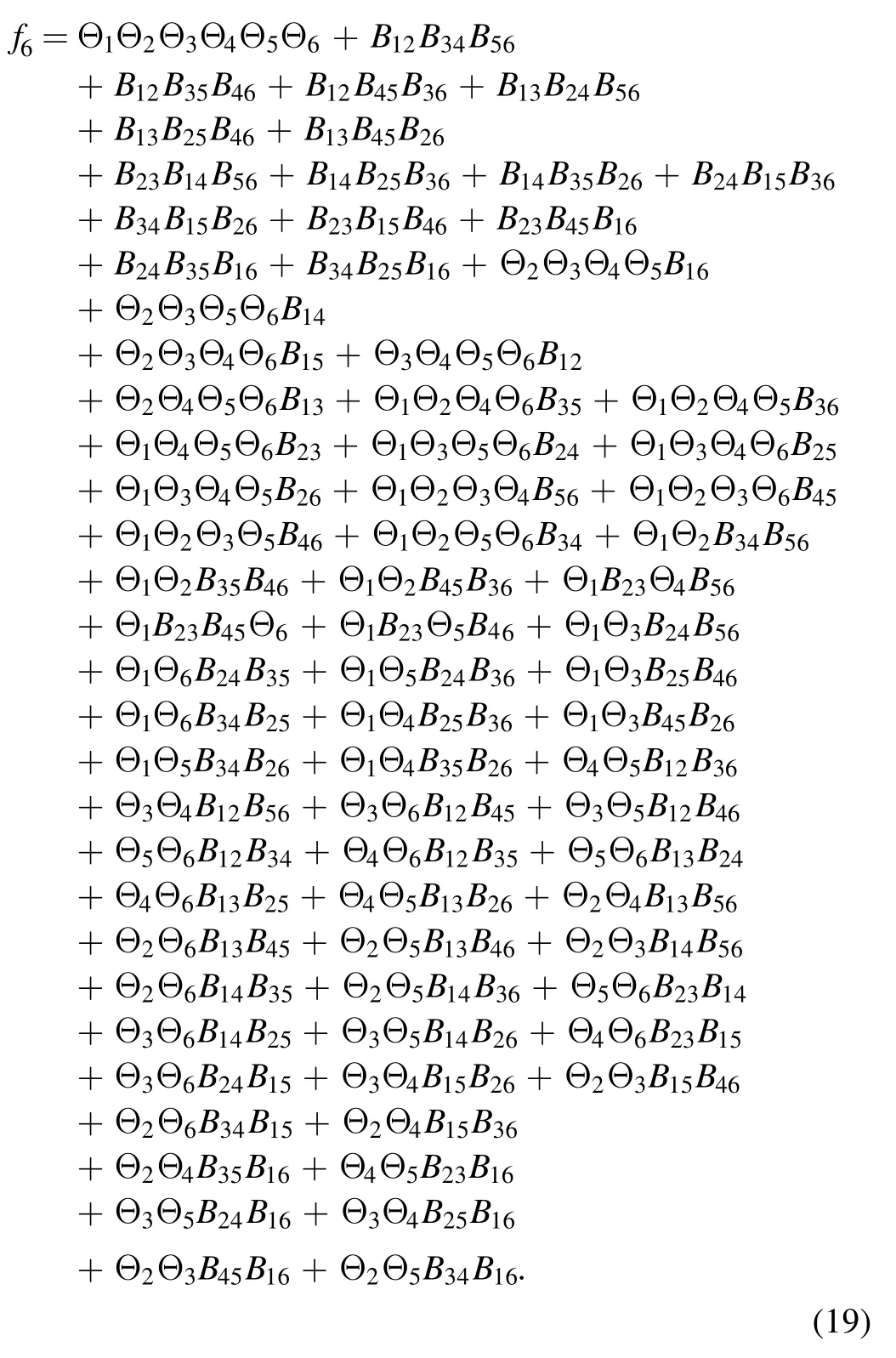

3.Collision phenomena


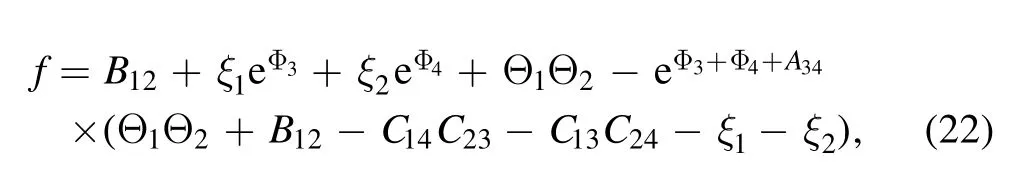

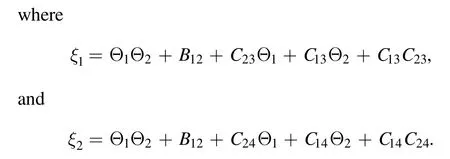
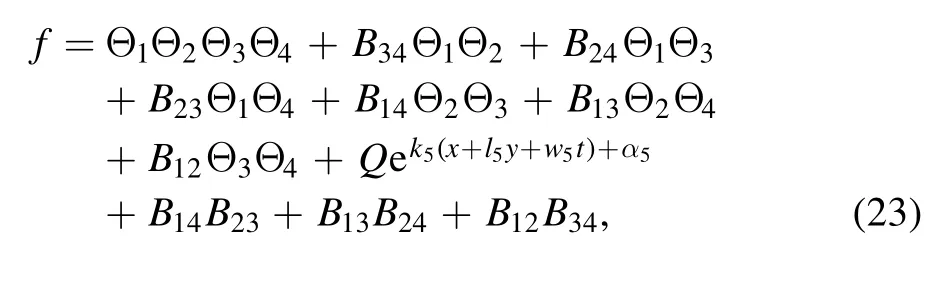

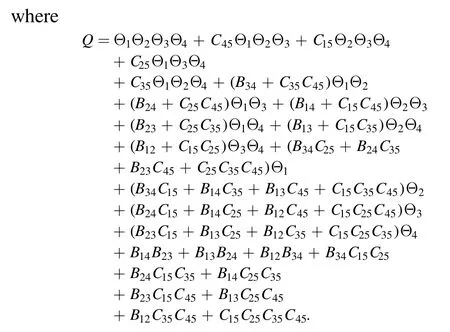
4.Breather solution and its interactions

5.Conclusions

杂志排行
Communications in Theoretical Physics的其它文章
- A numerical method to calculate dwell time for electron in semiconductor nanostructure
- Thermal Hall conductivity with sign change in the Heisenberg–Kitaev kagome magnet
- Dimensional crossover of a Rabi-coupled two-component Bose–Einstein condensate in an optical lattice
- Modification of laser-induced state in atomic attosecond transient absorption by the XUV pulse pair
- Optical forces on neutral atoms in the presence of fluctuating laser fields:numerical analysis
- High-sensitive refractive index sensing and excellent slow light based on tunable triple plasmon-induced transparency in monolayer graphene based metamaterial
