“实数”单元作业的设计、反馈与优化*

浙江省杭州市余杭区闲林中学 杨淑萍 程龙军

数学单元作业的主要功能在于巩固知识、诊断教学、学科育人.审视当下的单元作业，往往是只呼应一些低层次机械训练的作业目标，过度关注知识和技能的巩固，缺少对应于高阶思维和应用性的作业设计.这就需要我们在关注课程目标的同时，发挥数学作业的应有功能，适当增加创新性作业设计，助力课程目标的整体实现.为此，本文中以浙教版七年级上册“实数”单元作业设计为例进行说明.

1 作业目标

本章共分四个小节，主要内容包括数的开方、平方根、立方根、实数及其运算.其中，平方根与立方根属于核心概念.从操作意义上看，根号作为一个过程可以代表运算符号；从结构意义上看，它作为一个对象又可以代表运算的结果.与加减乘除运算相比，其概念抽象难懂，在处理具体问题时易混淆根号的过程性和结构性.基于此，在参考《义务教育数学课程标准》的基础上，作业目标可以适当增加抽象概念理解的相关内容.具体作业目标如下：

(1)加深对平方根、算术平方根、立方根、无理数、实数等概念的理解，知道开平方与平方、开立方与立方互为逆运算，实数与数轴上点的一一对应关系；

(2)会准确表示和计算一个数的平方根和立方根，能进行简单的实数四则运算，会估算一个无理数的范围，会求实数的相反数与绝对值；

(3)通过解决实际问题发展数感和符号意识，体会数形结合和分类讨论思想.

2 设计思路

为适应不同学生的学力水平，满足个性化的需求，作业设置分为回顾、强化、提升和应用四个层次.回顾环节帮助学生梳理知识点，形成知识结构；强化环节针对开平方和开立方运算进行专项训练，为后续学习二次根式的内容奠定基础；提升环节则综合多个知识点，考查学生分析和解决问题的能力；应用环节结合生活中的实际问题，使学生感受学习相关知识的必要性和应用价值，发展学生的应用意识和创造性思维.

3 初次设计及反馈

3.1 回顾

(1)下列说法错误的是( ).

A.无理数就是无限不循环小数

B.算术平方根等于本身的数是0和1

C.正数，0，负数都有立方根

D.因为3的平方是9，所以9的平方根是3

(2)填写表1：(不能开方的数写“无”，开不尽方的数保留根号.)

表1

(3)把下列各数填在相应的横线上：

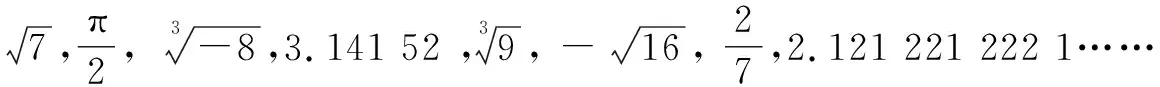
有理数：

.

无理数：

.

(4)将下列各数近似地表示在数轴上，并用“<”表示.

设计意图：第(1)(2)两题引导学生回顾平方根、算术平方根、立方根的概念以及性质，题中既包括了正数、负数和0，也包括了分数，目的是使学生对概念有全面的理解，同时也考查简单的开方计算.第(3)题考查了实数的概念与分类，重点让学生认清与π相关的数、开方开不尽的数、有规律但不循环的数这三类无理数.第(4)题考查了实数的大小比较和开立方运算，了解实数与数轴上点的一一对应关系，感受数形结合思想.

3.2 强化

设计意图：开方运算可为后续学习二次根式奠定重要基础.第①②小题强化考查平方根、算术平方根、立方根的计算；第③小题则考查学生对开方运算与乘方运算互逆关系的深刻理解；第④小题是较复杂的混合运算，需要运用乘法分配律以及计算器求无理数的近似值.

3.3 提升

图1

(7)如图1，每个小方格的边长为1个单位长度，则阴影正方形的面积是，边长是.

设计意图：第(6)题难度增大，综合了绝对值和算术平方根的概念、实数的加减运算以及分类讨论等多个知识点.第(7)题结合实际问题考查了面积法和开平方运算，强化了符号语言、文字语言和图形语言的相互转化，引领学生借助数形结合，直观感受无理数的大小和客观存在，克服理解数在扩展过程中的抽象性困难.第(8)题是新定义问题，涉及的知识点是夹逼法估算无理数和负数的大小比较.

3.4 应用

(9)小实同学手中有一块长方形纸板和一块正方形纸板，其中长方形纸板的长为3 dm，宽为2 dm，且两块纸板的面积相等.

①求正方形纸板的边长(结果保留根号)；

(10)小实手上有三张卡片，分别印有1，-125,196，请你从中抽出两张卡片，并以卡片中的数设计一个算式，要求算式中至少包括开方运算，且满足下列要求.

①结果为有理数：

.

②结果为无理数：

.

设计意图：本环节的两个问题基于开放性、探究性和趣味性的原则进行设计.第(9)题需要运用无理数处理实际问题，考查学生动手画图能力和对无理数的估算能力，培养数感和以形助数的意识.第(10)题兼具开放题和趣味性，借助“抽卡片”游戏考查学生对开方运算的理解.

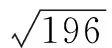
4 思考及优化

4.1 初次作业设计的思考

本次作业经课后统计，50%的学生在25分钟内完成，82%的学生在30分钟内完成.从反馈分析来看，此次作业量虽然符合作业要求，但部分试题难易不均、功能重叠，编排顺序也不够合理，因此进行如下思考与改进.

首先，回顾知识，厘清结构.设计作业时，需要注重单元知识间的相互联系，对教学内容进行结构化处理，帮助学生形成良好的认知结构.只有从单元整体上考虑作业设计、分析及评价，强调关联性，才能真正体现“整体架构”.纵观上述设计，缺少了一个梳理知识的结构化问题.

其次，基本概念，学深悟透.平方根和立方根的概念既是重点也是难点，从反馈的问题来看，学生对根号的认识不够清晰，不理解根号既表示开方运算也表示运算结果，以及在何种情况下表示运算而又在何种情况下表示结果.因此，对原第(1)题进行替换以加强学生对根号的理解.

再次，分层设计，优化细节.分层设计和循序渐进是作业设计的重要原则.第(6)题的知识点综合性强且错误率高，故将其与第(7)题调整顺序；第(10)题与第(9)题功能重叠，且思维含量不高，予以删除.

最后，降低难度，突出重点.强化训练是掌握数学知识的有效方法，但需要做到少而精，一味脱离对概念的理解而单纯搞题海战术，容易催生学生对作业倦怠，影响学生的学习兴趣.第(5)题中的③④小题运算难度较大，故进行替换以巩固实数运算的顺序和符号问题；第(8)题需要区分负数的整数部分和小数部分，还涉及负数的大小比较，对学生的理解和综合能力要求较高，也超出了课标要求，予以删除.

4.2初次作业设计的优化

4.2.1 回顾

(1)如图2，完善以下知识结构图：

图2

(2)下列选项正确的是( ).

(3)填表(如前表1)：(不能开方的数写“无”，开不尽方的数保留根号.)

(4)把下列各数填在相应的横线上：

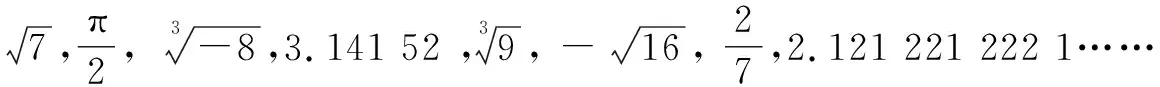
有理数：

.

无理数：

.

(5)将下列各数近似地表示在数轴上，并用“<”表示.

4.2.2提升

(7)如图1，每个小方格的边长为1个单位长度，则阴影正方形的面积是，边长是.

4.2.3 应用

(9)小实同学手中有一块长方形纸板和一块正方形纸板，其中长方形纸板的长为3 dm，宽为2 dm，且两块纸板的面积相等.

①求正方形纸板的边长(结果保留根号)；

5 几点建议

(1)问题设计的指向性

为了保证教学评的一致性,问题的设计需要与作业目标一致，教师需要细致分析相关知识点再进行精准设计，确立好作业内容后，依据目标逐条分析二者的对应情况，也可以做一些数据的分析和统计，进而对作业设计的内容乃至作业目标本身进行适当的调整.问题的设计还需要与课程标准倡导的“四基”相联系，既要指向基础知识和基本技能，也要指向基本思想方法和基本活动经验.此外，还要重视作业与课堂教学内容的紧密结合，既要面面俱到，又要杜绝知识点的简单重复，力求指向学习重点，充分发挥作业巩固知识和诊断的教学功能.

(2)问题序列的层次性

作业设计需要考虑不同学生的个性化学习需求，既要巩固基础，让学生感受学习的乐趣，也要提升和应用，让学生对知识有更深层次的思考.本单元作业设计了回顾、强化、提升和应用四个层次，难度由浅入深，尊重了学生的个体差异.回顾部分指向基础知识和基本技能，要求所有学生都要掌握，这也是课程标准的基本要求；提升部分强调知识的综合运用，要求中等生和学优生会做；应用部分对学生的理解和应用能力要求较高，学生可根据自身实际能力选做.

(3)问题设计的创新性

王月芬博士指出，作业类型的多样化有助于提髙学生的作业兴趣，减轻作业压力，同时对提高学生学业成绩也存在较明显的相关性.因此，数学作业类型和作业功能需要创新，由传统的只重视双基训练向重视综合能力的培养转变，充分发挥数学开放题、变式题、探究题以及综合实践题的育人功能.通过开放题培养学生思维的发散性，拓展思维空间；通过变式题引导学生迁移运用，完善知识体系；通过探究题培养学生思维的深刻性，感受数学之美；通过实践题体会数学与生活的密切联系和多样的学习方式，培养学生积极思考和主动探索的精神.