某水库防渗墙设计及地质构造影响下的渗透与应力特性研究

2023-02-15邹福华

水利技术监督 2023年1期

邹福华

(江西省水利水电建设集团有限公司，江西南昌 330000)

1 概述

防渗墙是水库坝体等水工建筑中常见的防渗结构设施[1-2]，研究防渗墙结构体系设计，有助于提高水工建筑防渗水平，推动水利设施安全高效运营。在水利工程建设中，地质构造活动常为不良因素[3-4]，可采用避开或治理措施，解决地质构造对水工建设的影响。刘菊莲[5]、林小聪[6]为探讨防渗墙结构设计，从水工建筑三维渗流场特征演变入手，借助Fluent流场模拟平台，开展了防渗墙设计方案的比选，为工程建设提供重要参照。防渗墙对水工建筑的影响不仅在渗流场中得到体现，同样作用于结构应力、变形，唐友山等[7]、温立峰等[8]借助ANSYS或Abaqus等有限元计算方法，从防渗墙结构的拉、压应力影响变化，以及各向位移值的演变，评价防渗墙设计方案的优劣性。地质构造包括有节理、断层带等，龚振[9]、杨顺刚[10]为研究断层等地质构造对水工设计影响，结合应力分布、流场演变特征等，综合评价断层对防渗墙设计、主坝运营等影响，为不良地质构造的治理设计以及水工参数设计等提供依据。

2 研究概况

2.1 工程分析

某水库是锦河北岸苏溪河支流重要水利枢纽，控制着苏溪河与锦河汇流区水位、泄流量等，所处坝址距离苏溪河与锦河交汇区下游15km，承担着高安乃至宜春地区重要防洪、输供水。2020年汛期，该水库的多梯度调节水位，控制泄流量等排洪措施，缓和了宜春、高安地区防洪挑战，但同时也发现了水库部分水工建筑无法满负荷运行，甚至部分水利设施出现“罢工”状态。在该年度过后，该水库管理部门考虑针对各类水工建筑开展汛后维修加固，确保水库运营安全稳定。水库除险加固工程平面布置如图1所示，工程建设内容包括有各梯级进、出水渠段重修以及主、副坝加固。该水库主坝为砂砾石心墙坝设计形式，堆筑料包括有砂砾石、反滤层、粉质黏土心墙垫层以及下游砂砾石、排水渠沟等，其断面如图2所示。从主副坝运营状况及坝基钻孔资料调查得知，上覆盖第四系土层包括了3层不同粒径及地质年代的砂砾石，总厚度超过50m，且在坝体K3+62处具有一处隐伏断层，延伸断面长为200m，宽度为14.5m，发育有砾石碎料夹层。基于上述考虑，工程部门计划在增设主坝防渗墙的前提下，探讨该隐伏断层对主坝防渗墙结构体系影响。

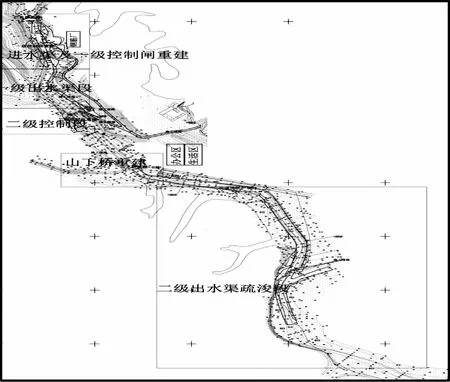
图1 高安水库除险加固工程平面布置

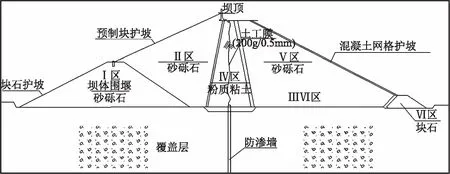
图2 坝体标准断面示意

2.2 建模分析

根据地质雷达探讨隐伏断层出现的断面前、后桩号175m区域，获得断层分布电磁特征[11-12]如图3所示，断层倾角为75°，岩性分布为砾石层，延伸长度为80m，而后续与之侵入接触面的为延伸5m的泥质灰岩，从该岩性直至桩号K3+212处。断层带内各岩性含水率分布为8.5%～11.3%，密度为1.98～2.06g/cm3，断层岩体弹性模量为10GPa，断层蔓延深度还未可知。本文一方面需探讨主坝防渗墙结构设计合理深度，也需针对隐伏断层特征开展防渗墙结构应力、渗透影响分析。

图3 断层分布电磁特征

为此，采用Abaqus仿真计算平台建立水库主坝模型，如图4(a)所示。该模型计算范围包括了断层与防渗墙结构，断层深度根据模型影响范围设定，延伸深度为120m，渗透特性计算参数按照片麻岩基岩取值。根据断层所在位置截取其中前、后175m为独立模型，如图4(b)所示，将该模型视为独立计算维度，其中x～z正方向分别为主副坝延伸向、上游苏溪河水流向以及坝体结构自重上方向。全模型中共有单元网格221674个，节点数168246个，采用三自由度六面体为计算单元。设定模型底面分别无水系交换边界，左、右2岸侧均为固体边界，按照竣工期设定上、下游静水压力荷载条件。心墙堆筑坝各类土体渗透及物理力学参数按照室内土工实测取值，如砂砾石层渗透系数为10-5m/s，排水沟渠渗透系数取值为0.01m/s。

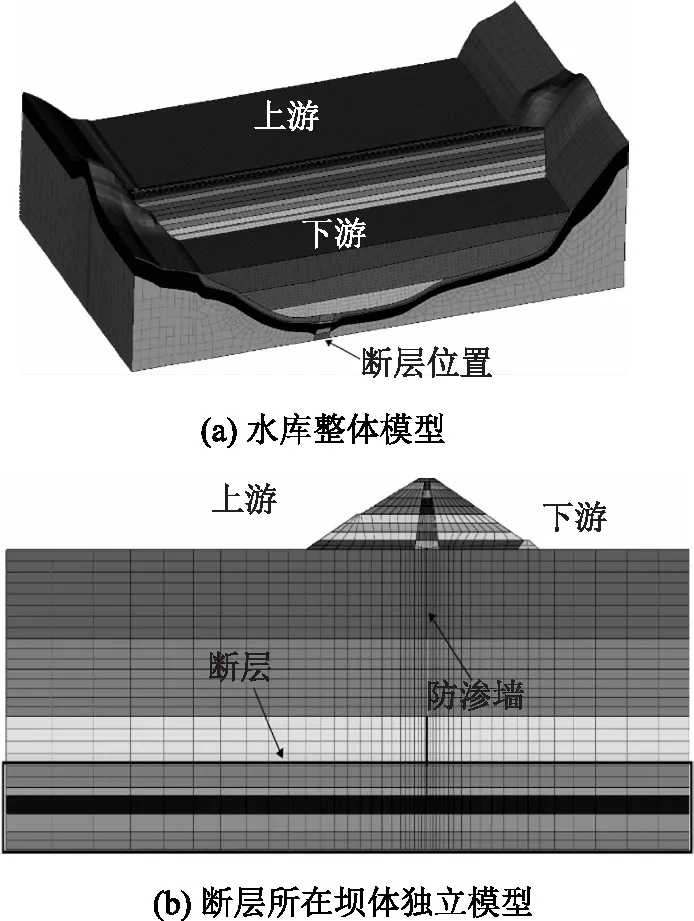
图4 计算模型

根据本文研究对象，沿着防渗墙深度梯次变化，计算防渗结构渗透特性以及应力分布特征，各方案中心墙坝体物理力学参数以及隐伏断层特征均保持一致。因而，设定防渗墙深度从0～120m梯次变化，阶次为20m，共有7个研究方案。在确保防渗墙深度为最优设计合理值的前提下，对隐伏断层影响下的防渗墙应力特征开展计算，由于断层延伸深度不同，则弹性模量有所差异，因而以断层弹性模量为研究因素，设定其弹性模量从10GPa逐步按照10倍递减，分别有模量10、1、0.1、0.01、0.001GPa共5个研究方案。基于上述研究方案，探讨主坝防渗墙结构设计以及隐伏断层等不利地质构造的影响。

3 不同深度处主坝防渗墙渗透与应力特性

3.1 防渗墙渗透特征

基于防渗墙不同深度下渗透特征计算，获得主坝渗流量与防渗墙深度变化特征，如图5(a)所示。由图5(a)可知，防渗墙深度愈大，则水库主坝渗流量愈低，且降低趋势呈逐渐减小变化，在防渗墙深度为0m时，主坝渗流量为1.5m3/s，而随防渗墙深度增大至20、60m时，相应的主坝渗流量较之前者分别减少了19.4%、93.2%，而防渗墙深度为80、100、120m时，主坝渗流量基本为0，处于较恒定状态。由此可知，防渗墙深度超过80m以后，实质上主坝渗流量即满足蓄水要求。

防渗墙深度影响下水库主坝、防渗墙结构上渗透坡降变化特征图如图5(b)所示。由图5(b)可知，当防渗墙深度递增，主坝出逸点渗透坡降呈递减变化，变化特征与渗流量有所类似，降低幅度在防渗墙深度80m后趋缓，渗透坡降也在此之后趋于0，但在防渗墙深度从20m递增至60m的过程，渗透坡降平均降幅可达89.3%。相比之下，改变防渗墙深度，防渗墙自身水力坡降变化幅度较低，各方案间渗透坡降最大幅度不超过6%，维持在1.98左右。综合渗透坡降影响变化可知，主坝渗透坡降乃是防渗墙设计尤为关注的重点[5，13]，防渗墙深度在80m左右坡降即较稳定。

图5 防渗墙深度对渗透特性影响

基于渗透特征计算，获得典型防渗墙深度下坝体断面上压力水头等值线分布特征，如图6所示。由图6可看出，在防渗墙迎水侧，由于覆盖层透水性特征，因而各水头等值线均处于平行状态；在坝体无防渗墙时，坝体背水侧水头值与上游基本持平，当防渗墙深度递增，防渗墙底部压力水头绕过防渗墙，在下游形成恒定水头值，而无法越过的水流在下游侧压力水头均呈减小变化，即防渗墙在所处深度范围内具有较显著抑制渗透的防渗效果。

图6 坝体断面压力水头等值线分布

3.2 防渗墙应力特征

根据对不同防渗墙深度下坝体第一、第三主应力特征分析，获得了计算结果如图7所示。分析图7中应力特征可知：①防渗墙深度愈大，第一主应力随之递增，在深度20m时，其值为0.065MPa；而深度为40、60m时，第一主应力较之分别增长了21.1%、25.5%；在深度达到80m后，主应力趋于稳定。②在防渗墙深度为20m时第三主应力值为18.7MPa；而深度在60、80m时分别较之减少了8.7%、20%；在防渗墙深度80m后，第三主应力处于趋缓稳定变化特征。

图7 防渗墙深度影响下应力特征

防渗墙深度为80、120m时第三主应力变化特征如图8所示，第三主应力等值线分布近乎一致，且均呈坝顶至坝底递增变化[7，14]。当主坝防渗墙深度设计为80m左右时，此时坝体应力分布亦较为安全。

图8 第三主应力变化特征

4 断层特征对主坝防渗墙应力变形影响

基于不同弹性模量的断层影响下，选择防渗墙深度80m为计算方案，获得防渗墙结构应力变化特征如图9所示。由图9中可知，当断层弹性模量递减，实质上乃是断层影响深度逐步扩展的过程[9]，在各方案中第一主应力呈小幅递增-递减至稳定，且仅维持在断层弹性模量的10～0.1GPa方案中。第一主应力最大值分别为0.04、0.052、0.06MPa；而在弹性模量0.01、0.001方案中，第一主应力处于较稳定状态，接近弹性模量10、1GPa方案下应力。由此表明，在断层扩展深度逐步增大过程中，适配防渗墙深度80m时，结构主应力特征仍维持较合理水平。

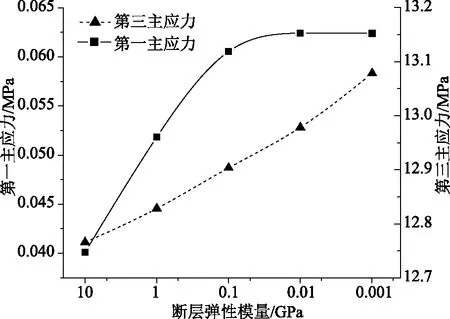
图9 断层特征影响下防渗墙结构应力变化

4个典型断层弹性模量方案下坝体标准断面上z向位移等值线分布特征如图10所示。从图10中可看出，在断层弹性模量呈量级递减时，各方案下位移分布特征基本一致，不论断层弹性模量为0.01GPa或为10GPa，坝体标准断面上位移分布为5～50mm，表明断层弹性模量对坝体z向位移值影响较弱。由位移等值线分布来看，在防渗墙底部均有较大位移集中，如断层弹性模量10、1GPa时，当断层弹性模量逐步减少至0.01、0.001GPa后，防渗墙上位移等值线扩散至断层附近，即防渗墙满可在断层一定深度内限制其影响。