高速铁路钢轨波磨声振结合识别方法

2023-02-15黄哲昊刘金朝徐晓迪柯在田

中国铁道科学 2023年1期

黄哲昊，刘金朝，徐晓迪，柯在田

（1.中国铁道科学研究院研究生部，北京 100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081）

我国高速铁路线路进入了运营维护阶段，各种轨道病害也陆续显现。轨道短波不平顺是一种典型的轨道病害，通常由钢轨焊接接头不平顺、钢轨轨头波浪磨耗、擦伤或剥离掉块等因素引起［1-2］，在列车行驶时可引起车辆零部件的高频振动。常见的短波不平顺病害波长在300 mm 以内，通过轮轨间作用力激励，在列车轴箱处可产生较明显的动态响应。文献［3—4］利用安装在轴箱上的加速度传感器测量的振动信号对短波不平顺病害进行分析。文献［5—7］提出了利用轨道冲击指数（Track Im⁃pact Index，TII）、钢轨波磨指数（Steel Corrugation Index，SCI）评价高频动态响应振动信号中的冲击成分、周期性波磨成分的方法。在利用轴箱加速度传感器采集的振动信号分析评价轨道短波不平顺病害的研究和应用方面，已有较成熟的采集分析系统和评价体系。为了更深入研究各种轨道病害的特征，分析不同速度等级线路病害间的关联性和演变规律，完善轨道短波病害的检测手段和评价体系，需要探索新的分析和评价方法。

国内外诸多学者研究了由轮轨相互作用而产生的振动和噪声机理及传播方式［8-9］，并利用传声器单元、传声器阵列采集列车行驶时的声信号，从声信号中提取轨道病害相关的响应特征［10-12］。相比于振动信号，声信号的阶次较高，从某个激励源到传声器响应之间的传递路径较多，所以声信号所捕捉到的细节信息较多，包含较多振动信号不敏感的信息，但同时也引入了较多不必要的信息。以安装在高铁列车轴箱上的加速度传感器采集到的振动信号和转向架构架处的传声器采集到的声信号为例，均属于列车高频动态响应信号。振动信号的激励源主要为车轮不圆顺和钢轨不平顺，通过轮轨的相互作用传递至轴箱处；声信号的激励源除了轮轨之外还包含气动噪声、刚体辐射声、弓网辐射声、电器设备噪声等等。文献［13—14］基于传递路径对声信号的激励源分离方法进行了研究，论证了在轮轨关系方面，分离由轨道不平顺产生的动态响应信号具有可行性。利用加速度传感器采集振动信号较为直接，对特定激励的响应较敏感，但是传感器位置需要足够精确，并且相同激励源对不同车辆的响应存在一定的差异性。利用传声器采集声信号具有非接触的特性，并可以采用传声器阵列的形式，利用声振信号的不同特性和声振多传感器结合的方式，在分离不同激励源的响应信号、提取不同动态响应信号的共性、挖掘轨道短波伤损的动态响应特征及增强检测系统的鲁棒性和稳定性等方面均有较好的研究和应用前景。

本文从声振结合的角度，采用文献［7］中提出的能量因子EF和波磨指数SCI描述振动信号的时频特性，提出用声能量因子（Acoustical Energy Factor，EFA）和声波磨指数（Acoustical Steel Cor⁃rugation Index，SCIA）描述声信号时频特性的方法，并进一步提出用声振复合能量因子（Compound Energy Factor，EFC）和声振复合波磨指数（Com⁃pound Steel Corrugation Index，SCIC）评价钢轨波磨的方法。

1 能量因子和波磨指数

依据文献［7］中提出的方法，可快速计算出综合检测列车轴箱垂向加速度传感器采集的振动信号的能量因子EF和波磨指数SCI。EF在频域上定量反映了钢轨波磨周期性特征的能量集中程度。SCI在时域上定量反映了钢轨波磨的冲击特性，并结合滤波和归一化手段减少信号中的其他成分和随机因素。基于这2 个特征量的性质，采用对应声信号的声能量因子EFA、声波磨指数SCIA及声振复合能量因子EFC、声振复合波磨指数SCIC，多维度评判钢轨波磨的动态响应特性。

1.1 振动信号

轴箱垂向加速度传感器采集的振动信号的能量因子EF［7］计算过程如下。

（1）对时域离散振动信号xv(k)（k为信号的离散采样时间点）进行加权交叠平均法（Welch法）自功率谱估计［15］，得到自功率谱Pvv(f)。

（2）选取Pvv(f)的最大值对应的频率fm作为能量峰值频率。

式中：D为计算峰值频率能量的数据半宽度，取D=10。

（f）依据式（2）计算振动能量因子EF。

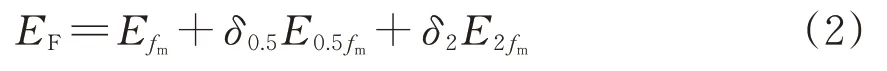
轴箱垂向加速度传感器采集的振动信号第i个样本的波磨指数SCI,i［7］定义为

其中，

式中：Si为振动信号第i个样本的移动有效值；Sˉ为所有振动信号样本移动有效值的平均值，该值与列车行驶的速度相关；K为移动平均的数据宽度，与列车行驶速度和采样频率相关，取K=2 400。

1.2 声信号

由于声信号与振动信号相似，同属于动态响应信号，可以按照1.1 节所述方法进行能量因子和波磨指数的计算。考虑到声信号本质是振动信号的高阶量，特定波长的钢轨波磨激励产生的声信号动态响应具有一定能量的高阶谐频成分，因此在计算能量因子时将峰值频率的1/2 倍频、2 倍频和3 倍频能量占比一同考虑。传声器采集的声信号的声能量因子EFA计算过程如下。

（1）对时域离散声信号xa(k)进行Welch 方法自功率谱估计［15］，得到自功率谱Paa(f)。

（2）选取Paa(f)的最大值对应的频率fm作为能量峰值频率。

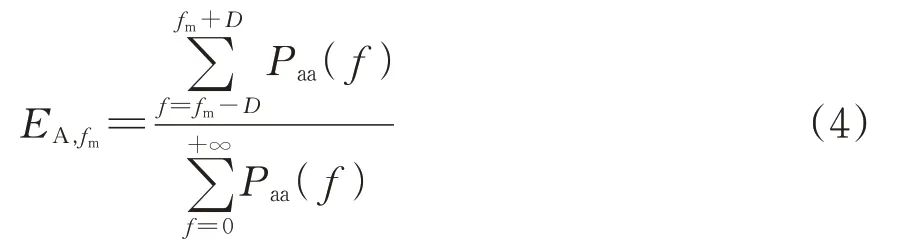
（4）将fm分别替代为0.5fm，2fm和3fm，依据式（4）计算该峰值频率的1/2 倍频、2 倍频和3 倍频的声能量占比

（5）依据式（5）计算声能量因子EFA。

参照振动的波磨指数形式，提出构架处传声器采集的声信号第i个样本的声波磨指数SCIA,i，定义为式（6）。

其中，

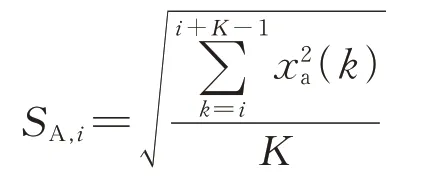
式中：SA,i为声信号第i个样本的移动有效值；为所有声信号样本移动有效值的平均值，该值与列车行驶的速度相关。

1.3 声振复合信号

钢轨波磨激励产生的声振动态响应信号所包含的信息成分具有共性和差异性，为了增强声振信号的共性特征、抑制声振信号的差异性特征，用复合能量因子和复合波磨指数反映钢轨波磨的动态响应特征，增强钢轨波磨本质特征在动态响应信号上的反映。

利用式（2）和式（5）进行推演，声振复合能量因子EFC计算过程如下。

（1）对离散时域信号xa(k)，xv(k)进行Welch方法互功率谱估计［15］，得到声振信号互功率谱Pav(f)。

（2）选取Pav(f)的最大值对应的频率fm作为能量峰值频率。

（3）依据式（7）计算该峰值频率附近的能量占比EC,fm。

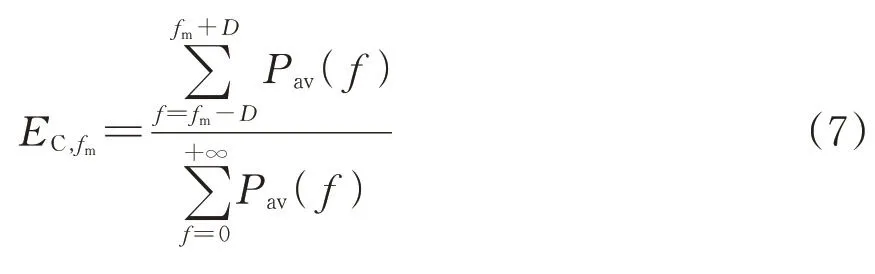
（4）将fm分别替代为0.5fm，2fm和3fm，依据式（7）计算该峰值频率的1/2 倍频、2 倍频和3 倍频的复合能量占比

（5）依据式（8）计算复合能量因子EFC。

利用Welch互功率谱估计法的特性，在频域上对声振信号的共有特性有一定的增强作用，对声振信号的差异性有一定的抑制作用。钢轨波磨的周期性特征能同时反映到声振动态响应信号上，互功率谱便具有增强周期性特征的能量集中度的作用。

参照SCI,i和SCIA,i的形式，将声振信号第i个样本的复合波磨指数SCIC,i定义为式（9）。

其中，

式中：SC,i为声振复合信号第i个样本的移动有效值；为所有声振复合信号样本移动有效值的平均值，该值与列车行驶的速度相关；α为幅值修正系数；∆k为相位修正的偏离点数。

SCIC,i同时包含了声振信号第i个样本的信息，与SCI,i和SCIA,i不同之处主要有以下2点。

（1）SCIC,i的定义式多了1 个系数α，α表征了EFC相对于EF和EFA的变化率，反映出互功率谱对声振信号中周期性特征成分的增强程度。SC,i可大致看作是声振时域信号有效值的几何平均，当其中1 个信号强度较弱时，SCIC,i值会降低，但信号如果存在较强的周期性特征时，希望SCIC,i能不受信号低幅值的影响，因此增加了幅值修正系数α进行弥补。

2 实测声振信号对比

本节选取3 种典型波磨区段的数据，将前节所述的3种能量因子和波磨指数应用于该数据的分析和评价。数据为国内某高铁线路上高速综合检测列车采集的轴箱加速度和声压信号，采样频率均为10 kHz，信号长度均为1 s，对原始声振信号均先采用等波纹FIR带通滤波器滤波，并保证通带内信号可覆盖波长为20～300 mm范围内的钢轨波磨。

2.1 振动信号响应较强的疑似波磨区段

振动信号响应较强的疑似波磨区段（A 类区段）振动信号的动态响应幅值较强并带有周期性成分，疑似存在钢轨波磨。该区段列车行驶速度为205.3 km·h-1，对声振信号进行0.19～2.85 kHz带通滤波。左轴箱处垂向振动信号和左构架处声信号滤波前后的时域声振信号如图1所示。

图1 A类区段时域信号

计算声振信号的自功率谱和声振互功率谱幅值如图2所示，图中已将频率轴换算为波长轴。

图2 Welch功率谱估计

由图2 可以看出：区段含有周期性成分，波长为74.6 mm；振动信号的频谱成分较为单一；声信号中存在一定能量的该周期性成分的2 倍频、3 倍频成分，但由于声信号的能量较小，互功率谱也仅存在单一的74.6 mm波长成分。

计算得出74.6 mm 波长波磨成分的3种能量因子见表1。由表1 可知：该例中振动信号的能量集中度很高，声信号虽然幅值较低，但仍有一定的能量集中度，因此声振互功率谱的能量集中度依然保持在较高水平，可以判定该区段存在周期性轨道伤损。

表1 波长74.6 mm成分能量因子

3 种波磨指数变化情况如图3 所示。由图3 可以看出：振动的波磨指数在部分区段超过了6，依据动态响应系统的阈值，判定该区段存在波磨；虽然声波磨指数较小，但由于周期性成分的能量集中度较高，导致复合波磨指数超过了4，依然较高。

图3 波磨指数变化曲线

对该区段的短波不平顺性进行现场复核如图4和图5 所示。由图4 和图5 可以看出：现场复核显示存在波长为74.5 mm 的周期性打磨痕迹，与分析的结果基本吻合。

图4 该区段现场照片

图5 该区段现场复核结果

该区段的情况说明，声信号一定程度上可以作为振动信号的补充，在小幅值的情况下依然能拥有周期性病害的典型特征，声振结合亦可判定该区段存在波磨。

2.2 声信号响应较强的疑似波磨区段

为了说明前节中的能量因子和波磨指数并不是全由振动信号贡献的，选取1 个声信号较强而振动信号较弱的疑似波磨区段（B 类区段），该区段列车行驶速度为154.7 km·h-1，对声振信号进行0.143～2.15 kHz 带通滤波。左轴箱处垂向振动信号和左构架处声信号滤波前后的时域声振信号如图6 所示。由图6 可以看出：时域振动信号较难看出周期性成分，但时域声信号表现出明显的周期性成分。

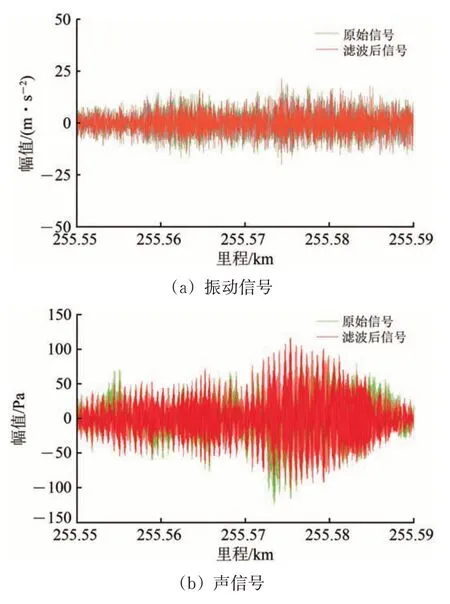
图6 B类区段时域信号

计算声振信号的自功率谱和声振互功率谱幅值如图7 所示，图中已将频率轴换算为波长轴。由图7 可以看出：区段含有周期性成分，波长为76.4 mm；振动信号存在一定程度的2 倍频成分，但存在一定的干扰成分；声信号在主频附近存在2 个较小的干扰频率成分，未存在谐频成分；通过声振结合，较强峰值仅存在于波长76.4 和38.2 mm 处，即主频成分与其2 倍频成分得到了保留，其他频率的干扰成分得到了有效抑制。

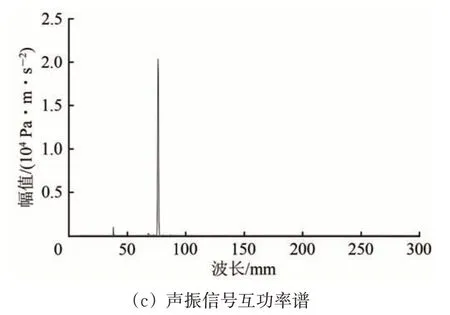
图7 Welch功率谱估计

计算得出波长76.4 mm 成分的3种能量因子见表2。由表2 可知：信号中的周期性成分很强；虽然振动信号的幅值不高，能量因子仅有0.626，声能量因子较高，为0.816，但通过声振结合，能量因子提高到了0.940，有效地抑制了周期性成分以外的信号成分，提高了能量集中度。

表2 波长76.4 mm成分能量因子

3 种波磨指数变化情况如图8 所示。从图8 可以看出：相较于最高值接近6的声波磨指数，复合波磨指数有所下降，但最高值依然接近4。

图8 波磨指数变化曲线

对B类区段的短波不平顺性进行现场复核如图9和图10所示。由图9和图10可以看出：现场复核显示存在波长为76.2 mm 的周期性打磨痕迹，与分析的结果基本吻合。

图9 B类区段现场照片

图10 B类区段现场复核结果

B 类区段的情况说明，在部分振动信号较弱的情况下，声信号却可能存在较大的动态响应，从频谱和能量因子可说明该区段的确存在周期性病害，声振结合能清晰地提取出周期性病害的特征，从而达到诊断评价波磨的目的。

2.3 疑似早期波磨区段

为了更明显地说明声振结合具有抑制信号差异性和增强信号共性的特征，并能识别早期短波伤损，选取动态响应能量较小但周期性较强的疑似早期波磨区段（C 类区段），该区段列车行驶速度为243.8 km· h-1，对声振信号进行0.225～3.386 kHz带通滤波，滤波前后的时域声振信号如图11所示。由图11 可以看出：此区段的振动响应和声响应幅值相当，但振动信号有较明显的周期性成分。

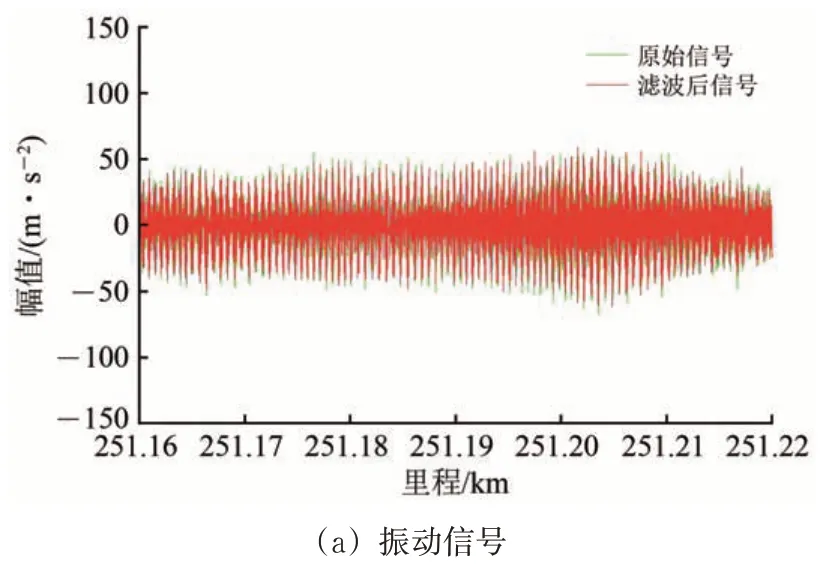
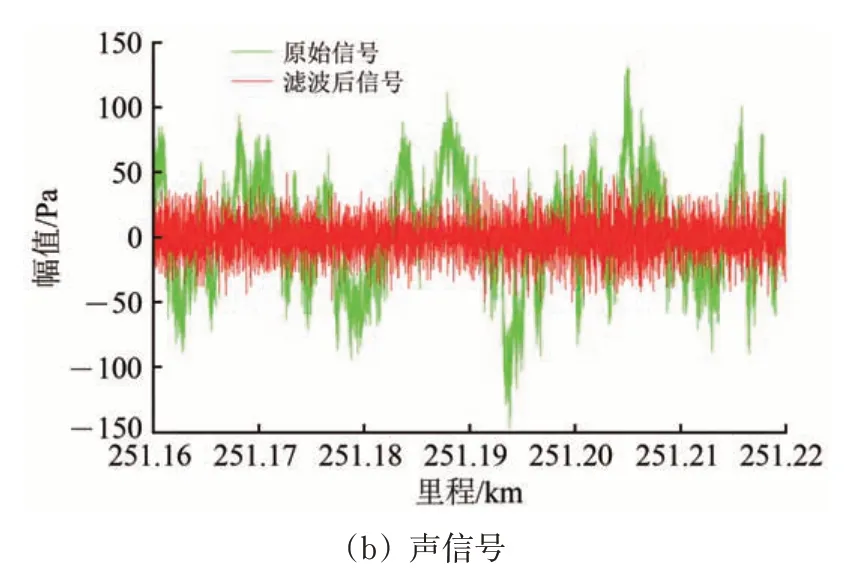
图11 C类区段时域信号

计算出声振信号的自功率谱和声振互功率谱幅值如图12所示，图中已将频率轴换算为波长轴。

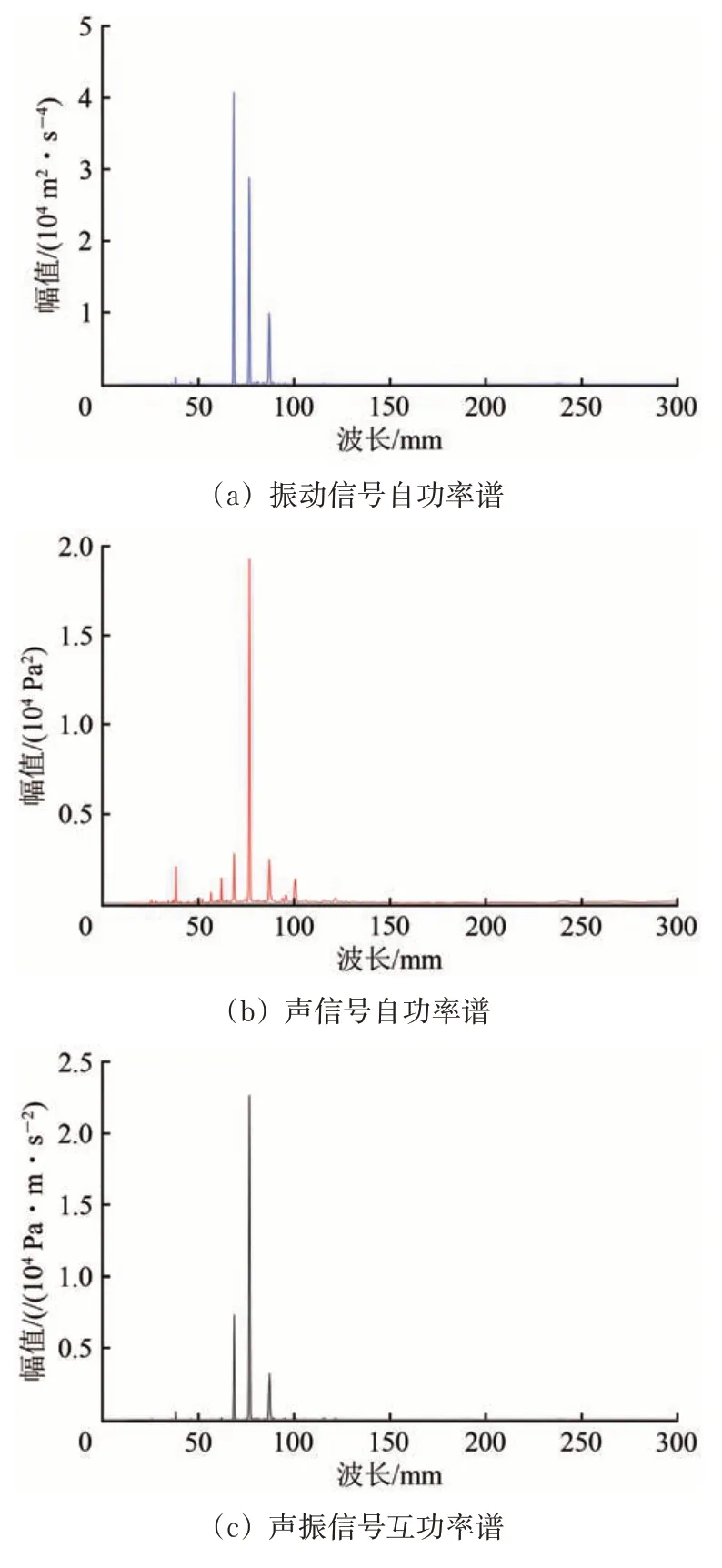
图12 Welch功率谱估计

由图12 可以看出：振动信号在波长为68.6，76.6 和87.0 mm 处存在频谱峰值，而声信号主要峰值波长为76.6 mm，存在对应波长为38.2 mm的2 倍频，并具有多个频谱峰值；声振互功率谱反映出不同频率的周期性成分在得到一定的抑制或增强后，保留了波长为76.6 mm 的主要频率成分以及该波长对应频率附近2 个频率成分的峰值，可以初步判断该区段存在多种复合周期性伤损；从时频数据上呈现出较强的包络调制现象可以推测出，该区段可能存在车轮不圆、Pinned-Pinned 共振等伤损，通过波长为76.6 mm 的周期性伤损激发，形成了频谱上主频附近局部峰值的调制现象。

计算得出波长76.6 mm 成分的3种能量因子见表3。由表3 可知：虽然声振信号单独的能量因子并不高，但由于存在周期性特征，使得复合能量因子相比于单独的声、振能量因子有所提高。

表3 波长76.6 mm成分能量因子

3 种波磨指数变化情况如图13 所示。由图13可以看出：复合波磨指数也有一定的增强，最大值超过了4。

图13 波磨指数变化曲线

由于C类区段的信号能量较小，基于加速度的动态响应检测系统未判定存在波磨，因此没进行现场复核，但从分析的结果来看，该区段可能存在一定程度的早期波磨或者残留的打磨痕迹，与其他潜在轨道病害共同激发出多频率周期性动态响应信号成分。该例说明，在声振信号的幅值均较小的情况下，其中的周期性成分通过声振结合后会得到加强，在复合能量因子和复合波磨指数上也有较好的体现。并且通过声振结合的方法，能确定C类区段周期性信号的主要频率成分。