基于承台消弯作用的新型桩板墙结构

2023-02-15李安洪王金梅肖世国郭海强

中国铁道科学 2023年1期

杨泉，李安洪，王金梅，肖世国，郭海强

（1.中铁二院工程集团有限责任公司，四川成都 610031；2.西华大学建筑与土木工程学院，四川成都 610039；3.西南交通大学土木工程学院，四川成都 610031）

山区铁路沿线地形起伏大，受展线及工程投资影响，在斜坡地段、路桥及路隧过渡段、站场等区域常采用高填方路基［1］。长期以来，铁路工程中常采用桩板墙结构控制高填方边坡变形与稳定。与传统浅埋低矮支挡结构相比，桩结构具有刚度大、承载力高、支挡高度范围大的特点，在铁路填方工程中有着广泛的应用。

随着高速铁路设计时速不断提升，需要更加严格的控制高填方路堤变形以满足列车对平顺性的要求［2］，由此引起一系列新的设计问题。其中，土质条件下的桩板墙设计问题较为突出，主要难度体现在以下3 个方面。第一，经济性不佳，锚固桩的变形控制条件严格（锚固点水平位移不超过10 mm，桩顶水平位移不超过100 mm，高速铁路桩顶不超过60 mm）［3］，一般通过调整桩的截面尺寸或桩长改善结构刚度达到设计要求，由于土质地基或风化较严重的岩石地基的地基系数较小、土抗力有限，即便填方高度较小时桩身的设计尺寸也较大，因此当地质条件不佳时，工程成本及施工难度可能成倍增加。第二，截面尺寸优化设计极为困难，施工时桩板墙的桩身结构为一次性整体浇筑成型，一般情况下锚固段截面尺寸与悬臂段一致，但实际受力情况是悬臂段桩身挠曲变形占桩顶总变形比例极小，导致悬臂段桩身截面利用率极低。以10 m 高悬臂桩为例，在一般土质条件下截面尺寸采用1.8 m×2.5 m 可满足设计要求，当填方高度增加至12 m 时，桩的截面尺寸需增加至2 m×3 m，工程量增加约1/3。从结构受力特征可知，采用悬臂段与锚固段的变截面设计模式可在一定程度上优化截面尺寸，但也将导致模板搭建困难、施工缝控制桩身强度等新的问题。第三，支挡高度有限，路肩桩板墙悬臂段长度不宜超过12 m，因为过大的支挡高度会引起较大桩顶变形、导致设计截面尺寸过大，桩板墙结构形式已不是经济的选择。

国内外学者对桩板墙结构进行了大量研究。魏少伟等［4］对比分析了圆形与矩形截面抗滑桩抗滑性能，认为圆形截面抗滑桩的受力性能与矩形截面抗滑桩基本一致。董捷等［5］对桩板墙加固斜坡填方地基的土压力分布问题进行研究，提出了柔性板刚度与土压力关系。王潘［6］针对滑坡隧道偏压受力特点提出了辅底抗滑桩结构，解决了滑坡隧道变形控制问题。毛坚强等［7］基于m 法模型提出了滑体段抗滑桩计算方法。廖超［8］提出了h 型桩板墙结构并对该结构应用于高速铁路陡坡路基的设计参数进行分析，提出各子结构的尺寸建议值。吴江等［9］对高速铁路陡坡路基桩板墙侧向位移的影响进行分析，认为锚固桩侧向变形的横向影响范围为6～7.5 m。ZHANG 等［10］对带卸荷平台的桩板墙变形影响因素进行研究，分析不同深度位置的卸荷平台作用效果及受荷规律。王唤龙和周德培［11］建立了考虑土抗力的微型桩组合结构受压桩计算模型，基于伽辽金方程推导受压微型桩屈曲临界荷载的计算公式。肖武权和阮波［12］对中、大型滑坡整治中广泛应用的抗滑桩进行优化设计，基于多目标决策模糊集理论建立用于抗滑桩的目标特征值矩阵。蔺鹏臻等［13］根据边坡上桥梁桩基受力特点，建立考虑边坡效应的桩基础静力微分方程。刘鸿等［14］针对框架梁连接的微型桩组合结构，采用模型试验与有限元分析相结合的方法，对微型桩桩后土压力和桩身水平位移进行分析，研究微型桩组合结构抗滑机理。上述研究针对桩结构在不同领域的应用特点提出了有效的结构措施或计算方法等，而桩板墙结构在土质条件下设计尺寸较大，成本偏高的设计问题鲜有研究，对传统桩型结构进行合理改进，提高桩板墙变形控制效果以节省工程成本是土质条件下高填方路基修建技术亟待解决的关键问题，具有较大的经济实用价值。

针对传统桩板墙受力变形特点，在桩身的锚固点位置引入承台，提出一种基于承台消弯作用的新型桩板墙结构，并采用矩阵传递法分析其力学性能及经济效益。

1 新型桩板墙结构

根据桩板墙结构的受力特点，路肩桩板墙桩顶的水平位移s由悬臂段挠曲变形δ1、桩身整体平移δ2和转身绕锚固点旋转引起的桩顶水平位移δ3这3部分组成，如图1所示。s由下式求得

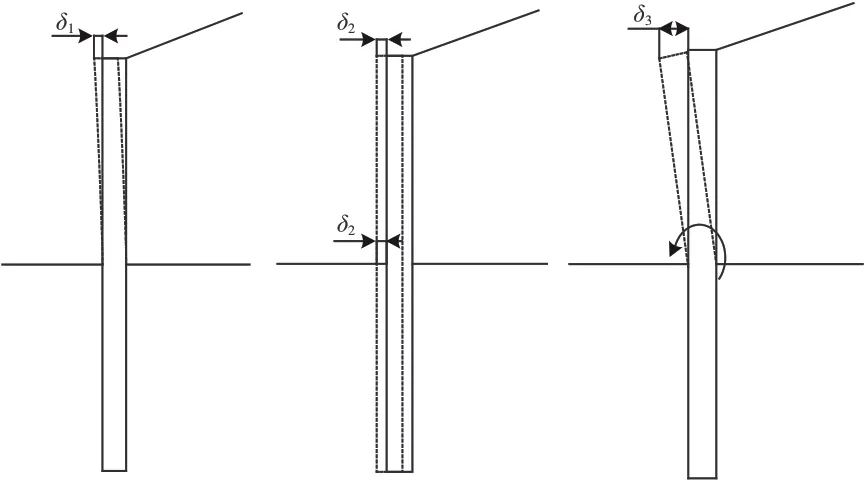
图1 桩板墙结构变形示意图

通过不同土质条件下的变形计算可知δ3>δ2>δ1，且各部分占总变形的比例大致为：δ1占比约为10%～20%，δ2占比约为10%～20%，δ3占比约为50%～70%。首先，在外部条件不变时，δ1由悬臂段桩身抗弯刚度控制，若要提升桩身刚度，仅能通过增加截面尺寸达到目的，由于悬臂段变形占总变形的比例较小，对整体结构的变形改善效率是极低的。其次，δ2主要受控于桩身有效宽度、刚度及锚固段土的横向抗力系数，土体的横向抗力系数取决于工程的地质条件，提升桩的有效宽度同样需要增加截面尺寸，且截面尺寸增加对桩的惯性矩提升影响较小，导致平移变形的控制也较为困难。因此，如何有效控制δ3是对桩板墙结构进行优化设计的关键。

新型桩板墙结构设计的核心思路是在锚固点位置引入与桩身刚接形成一体的承台结构，通过抵消悬臂段弯矩来减小桩身旋转引起的位移，进而减小桩顶变形。新型桩板墙结构及其受力如图2所示。

图2 新型板桩墙结构及其受力示意图

新型桩板墙结构依靠作用于承台填土的自重抵抗或消除悬臂段传递的弯矩，使锚固段桩身弯矩大幅减小，可有效优化桩截面尺寸。同时，施工方法完全参照桥梁基桩-承台的施工方法即可，属于成熟工法。新型板桩墙结构地面上、下部分可分开施工，可从以下两方面进行优化：桩基下部分可采用圆形灌注桩机械化施工代替传统人工挖孔桩，可有效提升现场安全文明施工的程度，避免塌孔、有害气体、机械倾倒等人工作业引起的潜在风险；悬臂段桩身可根据变形控制条件适当缩减截面尺寸，无须与锚固段截面尺寸相同，悬臂段桩身尺寸完全由上部水平土压力计算确定，由于桩身挠曲变形较小，桩身截面尺寸的缩减幅度较为可观。

2 新型结构计算方法

2.1 计算方法

新型桩板墙结构计算模型如图3 所示。图3中：OXY为整体坐标系，o1x1y1为桩悬臂段和锚固段的局部坐标系，o2x2y2为承台的局部坐标系；AC，BC 和CD 分别为悬臂段、承台和锚固段；q1x和q2x分别为作用于悬臂段和作用于承台上的土压力。新型桩板墙结构中桩的悬臂段、锚固段和承台均可视为文克尔弹性地基梁，因此可采用矩阵传递法［15］计算分析其内力变形。

图3 新型桩板墙结构计算模型

根据梁挠曲微分方程和弹性地基梁基本假定，梁单元的任一截面均满足以下控制方程

其中，

式中：y为垂直于梁的位移；x为距梁端的距离；λ为弹性地基系数；k为基床系数；b为梁的宽度；E为梁的弹性模量；I为梁的惯性矩。

将梁单元分解为n个微段，微段i的两端分别为第i-1 和第i个节点。Qi，Mi，ϕi和yi分别为第i个节点的剪力、弯矩、转角和竖向位移。

根据式（2），可得梁单元中第i-1 个节点至第i个节点的传递方程为

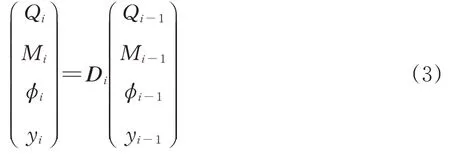
其中，

式中：Di为第i个微段的单元传递矩阵；λi，Δxi，Ei和Ii分别为第i个微段的弹性地基系数、长度、弹性模量和截面惯性矩。

悬臂段、承台和锚固段均可采用以上方法构建传递方程。以悬臂段为例，其在局部坐标系内的微段单元如图4所示。图中，qi为作用于微段i的外荷载。

图4 悬臂段微段单元

考虑悬臂段荷载条件，可得传递方程如下

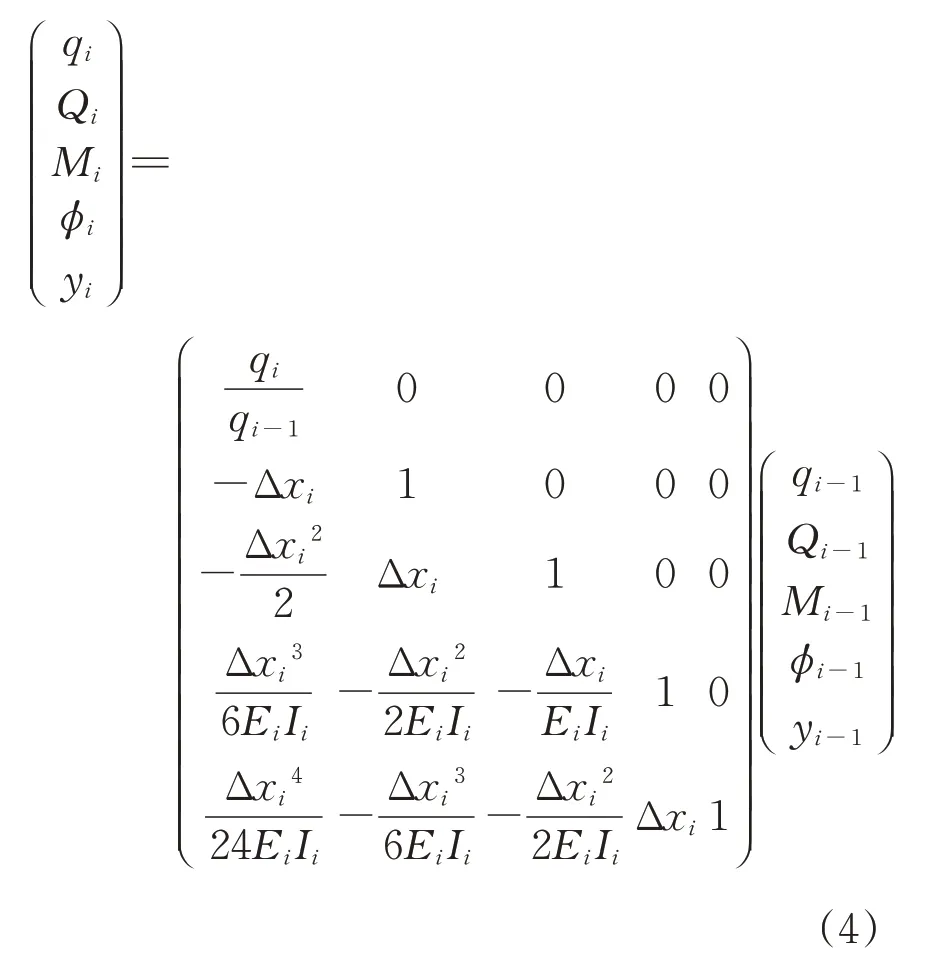
新型结构所有未知量包括3 个内力（轴力、剪力和弯矩）、3 个变形（轴向位移、竖向位移和转角）和1 个荷载，考虑桩身自重γ与侧阻力fs的影响增加2 个变量，因此传递矩阵为9 阶方阵。悬臂段的传递方程可由式（4）修正为

式中：Ai为第i个微段的截面面积。

则悬臂段第i个微段的单元传递矩阵DACi为

对于悬臂段，从A 端到C 端的总传递矩阵DAC为可由下式求得

类似地，可分别得到承台和锚固段的总传递矩阵DBC为DCD。

承台局部坐标系与结构整体坐标系不同，需进行坐标转换。根据图3 建立的整体坐标系，建立转换矩阵DT

对于节点C，则有

以截面A 和截面B 为求解目标，共有6 个位移未知量ϕA，yA，wA，ϕB，yB和wB，需要获取6个平衡方程。通过边界条件与变形协调条件建立平衡方程过程如下。

悬臂段顶部（截面A）和承台的端部（截面B）为自由端，内力均为0，即

土质条件锚固桩底部（截面D）为自由端，其剪力、弯矩、轴向位移均为0，即

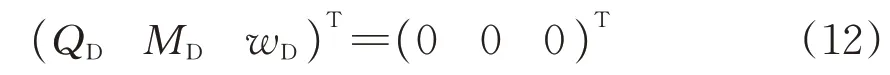
由节点C处变形协调条件可知

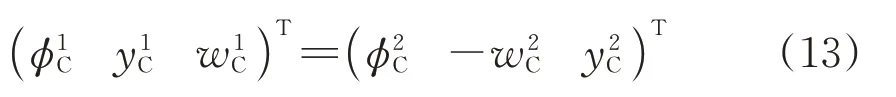
定义如下表示方法：A（i∶j，p∶q）表示由矩阵A第i到j行的第p到q列组成的矩阵。由式（13）可得

上式中，令

则式（14）可改写为

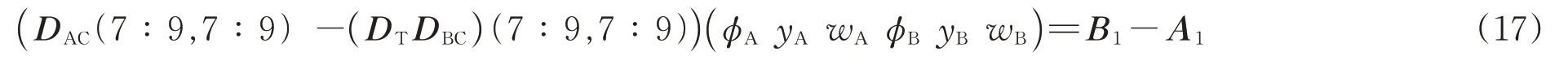
根据节点平衡关系，在C节点处，为实现将承台的内力传递给节点C且位移不传递的目标，令辅助矩阵De为

由D截面平衡条件可得

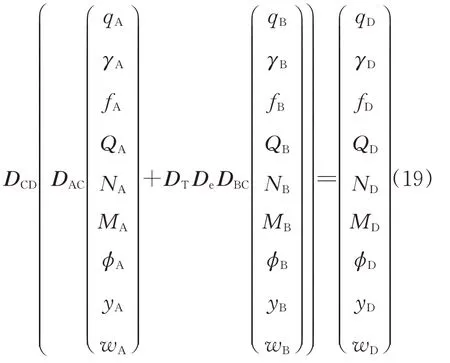
将式（19）展开后存在如下关系

将式（10）和式（11）代入式（24），即可求得截面A和截面B的6个位移未知量。

根据矩阵传递法，悬臂段内任一节点的内力和位移可由A 点的内力和位移求得；承台内任一节点的内力和位移可由B点的内力和位移求得；锚固段内任一节点的内力与位移可由C点的内力和位移求得，而C点的内力与位移可根据平衡条件求得。

2.2 方法验证

为验证本文计算方法可靠性，分别采用本文方法和常用桩板墙结构计算软件理正对传统的路肩桩板墙结构的内力变形进行计算分析，并对比其结果。采用本文方法计算时，将承台尺寸设为0 即可。参考工程中常用的结构尺寸及材料参数，本文算例参数取值见表1。

表1 结构尺寸及材料参数

图5 为本文方法与理正计算结果对比，高度为0 对应于地基顶面即锚固点位置。由图5 可知：总体上本文方法与理正的计算结果极为吻合，桩身弯矩最大误差为5.4%，桩身剪力最大误差为4.7%，水平位移最大误差为9.2%。理正软件的计算原理是首先按悬臂梁计算悬臂段底部内力与变形，再将其作为锚固段顶部的边界条件进行计算，得到锚固段全部信息。本文计算方法是将悬臂段与锚固段作为整体进行求解，此外，还可通过调整桩身分段数量来提升求解精度，这是导致两种方法产生误差的2 个重要原因。经对比验证，本文新型结构计算方法是正确可靠的。

图5 本文方法与理正计算结果对比

3 新型结构受力特性及关键设计参数

3.1 受力特性

采用本文计算方法对新型桩板墙结构计算分析，并与同尺寸的传统桩板墙结构进行对比。地基为土质地基，地基土与填料参数见表1。结构形式仍为路肩桩板墙，桩间距6 m，结构尺寸见表2。计算时不考虑列车荷载。

表2 桩板墙结构计算条件

新型桩板墙结构与传统桩板墙结构的计算结果如图6 所示。由图6 可知：在桩的悬臂段2 种结构内力、变形以及土反力计算结果高度吻合；新型桩板墙结构锚固段最大弯矩仅为传统桩结构的33.7%，桩顶水平位移仅为传统桩结构的39.2%，最大土反力仅为传统桩结构的43.1%。

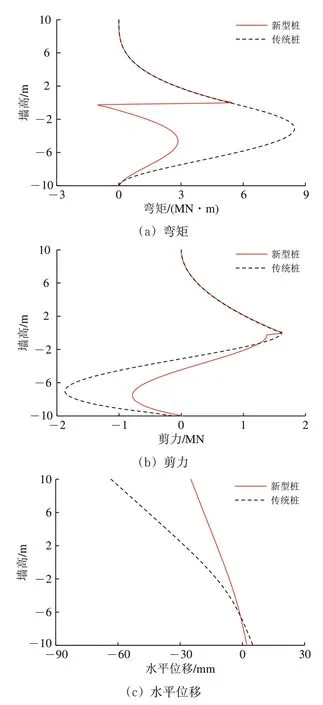
图6 新型结构与传统结构计算结果

可见，新型结构中的承台对桩悬臂段的受力变形基本无影响，但极大地减小了悬臂段传递到锚固段的弯矩，进而减小桩身旋转引起的位移、减小桩顶变形。与传统桩板墙结构相比，新型结构受力及变形得到较大改善，有更多的优化空间，达到设计初衷。

3.2 关键设计参数

填高（悬臂段高度）和承台尺寸是本文提出的新型桩板墙结构的关键设计参数，确定关键设计参数取值范围即结构适用条件可有效降低计算工作量，提高设计效率。

铁路支挡工程中，桩板墙桩顶变形控制标准为100 mm，锚固点变形控制标准为10 mm，墙高一般不超过12 m。为确定新型结构填高的适用范围，采用本文方法计算不同墙高的结构变形，并与传统桩板墙结构进行对比。计算参数及取值见表3，材料参数见表1。

表3 填高适用性计算参数

新型桩板墙结构和传统桩板墙结构水平位移随高度分布曲线如图7 所示，位移以向右为正。由图7 可知：在同一土质地基且截面尺寸、锚固桩长不变的条件下，传统桩板墙结构墙高超过12 m 后锚固点水平变形已远大于10 mm；新型结构墙高增加至16 m 时，对应的锚固点变形为10 mm，即新型桩结构的填高上限可达16 m。若继续扩大结构的适用高度范围，则必须通过增加桩的尺寸方能实现对变形的控制，但可能导致弯矩过大、增大承台尺寸，其经济合理性需另行研究。

图7 桩身水平位移曲线

承台尺寸的设计是决定本新型结构能否发挥结构受荷优势的关键。受相邻承台间距及施工条件影响，一般情况承台的宽度值不宜过大，按构造要求即可（承台宽度方向两侧各大于锚固桩边缘50 cm且不小于0.3 倍的锚固桩直径）［16］。承台的长度设计原则为：承台上覆土压力产生的弯矩基本能平衡悬臂段产生的弯矩，即尽可能使锚固桩顶弯矩接近为0。在此条件下，采用本文方法计算分析墙高为10～16 m时合理的承台长度，结果见表4。

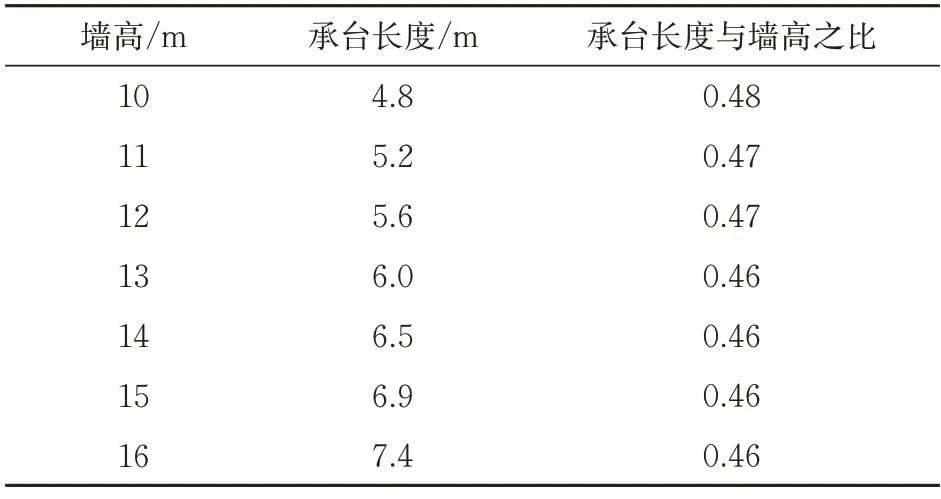
表4 承台长度计算结果

由表4 可知，合理的承台长度约为0.46～0.48倍墙高。当墙高较低或桩间距较大时可通过计算适当增加承台长度与填高比值。若受场地条件影响，承台长度方向受限时，也可增加承台宽度满足设计要求，承台长度仍可采用本文方法计算确定。

4 经济性分析

将新型桩结构拆分为锚固段、悬臂段和承台段，可分别计算各子结构在外力作用下的内力和变形。考虑到承台段提供的反弯矩对悬臂段根部弯矩的平衡作用，锚固段可进行大幅优化，新型结构的实际工程数量远低于传统结构。

为分析本文提出的新型桩板墙结构的经济性，分别对新型桩板墙（编号1#）、传统桩板墙（编号2#）和桩基扶壁式挡土墙（编号3#）进行比选。以弥蒙铁路路肩墙为例，工程设计条件如下：路基填方高度为8 m，路基面宽度14 m；基床采用A 组填料填筑，本体采用B组填料填筑；地基第一层为强风化泥岩层（W3），第二层为全风化泥岩层（W4）。图8为上述3类形式的高填方路肩挡土墙示意图。

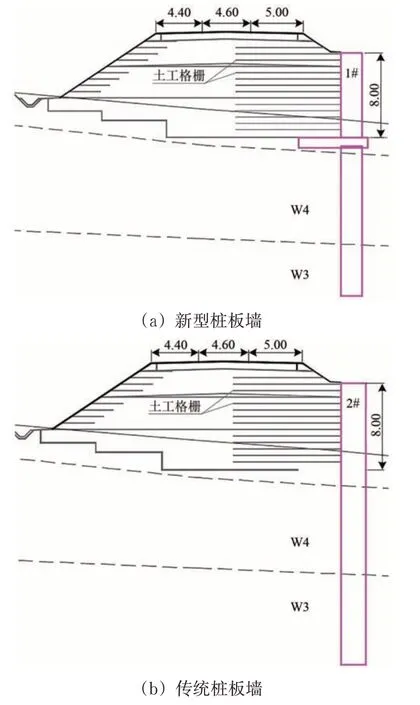
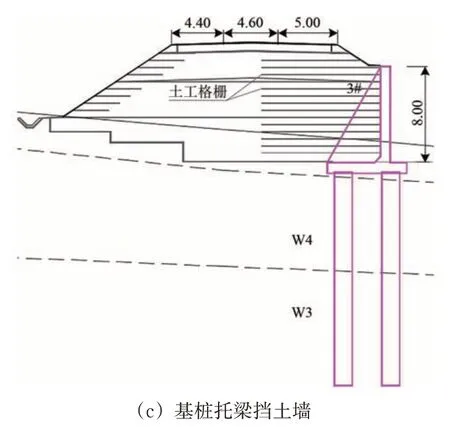
图8 高填方路肩挡土墙示意图（单位：m）

3 类结构形式锚固桩间距均为5 m。经设计后统计工程数量见表5。根据统计的工程数量计算单位工程（5 m 范围）的综合造价，得到如下结果：新型桩板墙15.3万元、传统桩板墙30.16万元、桩基扶壁式挡墙32.33 万元。在不考虑由承台施工产生的额外费用前提下，新型桩板墙节省投资约50%，经济效益显著。