高速铁路地基泥岩膨胀变形计算方法及应用研究
2023-02-15刘景宇张千里郭浏卉张新冈王鹏程王李阳
刘景宇,张千里,郭浏卉,张新冈,王鹏程,王李阳
(中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081)
我国地域辽阔,是世界上泥岩分布较广的国家之一。泥岩富含黏土矿物,遇水极易发生体积膨胀,导致铁路线路发生上拱变形,严重威胁铁路安全运营。而我国要形成以“八纵八横”主通道为骨架、区域连接线衔接、城际铁路补充的高速铁路网,就不可避免地要跨越泥岩地区。以西北某高速铁路为例,仅这1条线路就横穿了上百公里的泥岩地区,发生了20 多处由泥岩地基吸水膨胀引起的路基上拱变形病害,最大变形量超过50 mm,且变形仍在持续发展。对于毫米级控制标准的高速铁路而言,在泥岩地区段不得不采取顺坡、封闭、路基换填、基床表层切割或支承层切割等措施降低线路高程,以保证线路安全运营,这些措施不但治理成本高、风险大且治理不彻底,后期上拱变形仍持续发展。若在建设前期能够预测该泥岩的膨胀变形趋势,则建设期间就可采取换填、封闭或预留等方式进行处理,能够极大降低运营期的养护维修费用,减少列车运行安全风险。因此,造成现在以治理为主的主要原因是对泥岩膨胀的发展规律认识不清,缺乏针对泥岩膨胀变形的计算方法及预测模型。
泥岩是介于软岩与硬土之间的特殊材料,同时具有岩石的结构特征和膨胀土的膨胀特性[1]。工程建设前,泥岩周围环境稳定一般不易发生膨胀,当进行工程建设时,随着开挖卸载等活动的开展,泥岩周围应力环境发生改变,约束力变小产生次生裂隙,水分沿次生裂隙进入泥岩内部使其发生体积膨胀[2]。关于膨胀岩的计算,传统膨胀岩膨胀理论认为膨胀岩轴向应变与膨胀压力的对数呈线性关系[3-8],基于该理论,杨庆等[9-10]设计了膨胀岩的三轴膨胀试验,提出了膨胀岩的体积膨胀本构关系;膨胀发生的主要外在因素是周围水环境的改变,基于此,缪协兴等[11-13]提出了湿度应力场理论,通过膨胀岩周围湿度的变化对膨胀岩的体变进行计算与分析;朱珍德等[14]在湿度应力场理论的基础上进行了推导,获得了膨胀岩的弹塑性本构模型;刘晓丽等[15]、季明等[16]及左清军等[17]将膨胀的时间效应引入了计算模型。
查阅相关文献发现,以往针对膨胀岩计算的研究很多,但鲜有针对泥岩膨胀导致的基础及上部结构变形方面的定量计算。
本文将泥岩的吸水膨胀过程类比材料的吸热膨胀过程,提出基于热力学理论的泥岩膨胀变形湿度场理论,对高速铁路泥岩地基膨胀变形提供1个计算及预测方法。
1 计算方法与验证
1.1 计算方法
既有研究表明,在一定含水率条件下,泥岩的膨胀体变与含水率呈线性关系。以取自西北某高速铁路地基膨胀病害工点处泥岩(J1-2Ms)为例[1],该泥岩为侏罗系中下统泥岩,局部夹砂,青灰色,泥质结构,中厚层构造,泥质胶结,节理裂隙较发育,岩体较破碎(如图1 所示),其物理力学参数见表1—表3。

图1 工点处裸露泥岩

表1 泥岩基本物理力学参数

表2 泥岩全岩X射线衍射结果

表3 泥岩全黏X射线衍射结果
采用自主设计研发的三轴体变测量系统进行试验,获得泥岩在不同围压环境下的膨胀体变发展规律[1]。以围压100 kPa 为例,泥岩在该围压条件下吸水膨胀过程曲线如图2 所示。由图2 可以看出:在该条件下泥岩吸水膨胀过程表现为2 个阶段,即体变随吸水率的线性增长阶段以及稳定阶段;在一定吸水率条件下,泥岩吸水膨胀体变与吸水率呈线性关系。
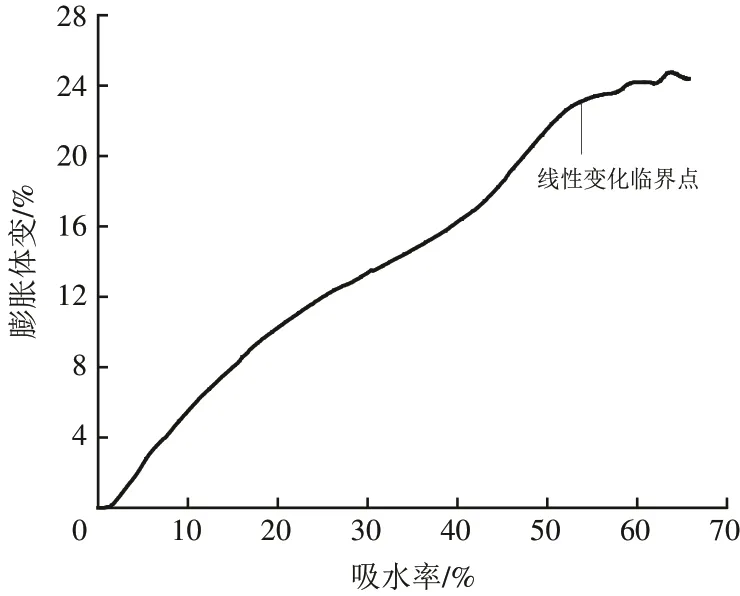
图2 围压100 kPa下泥岩吸水膨胀曲线
以吸水率40%为界限,对不同围压下的泥岩吸水膨胀曲线进行拟合,结果如图3所示。
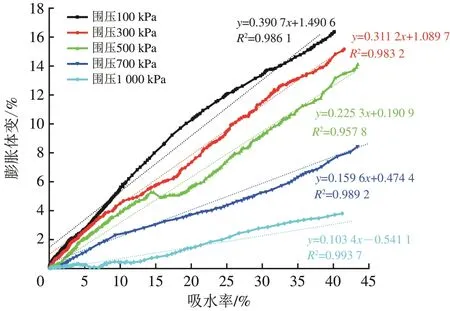
图3 不同围压下泥岩吸水膨胀曲线
由图2 和图3 可以看出:该泥岩在吸水率低于40%的条件下,膨胀体变与吸水率的线性相关系数在0.95 以上,可以明确在该吸水率范围内,泥岩的膨胀体变与吸水率呈线性关系;泥岩吸水膨胀失水收缩,这与热力学中材料的热胀冷缩规律一致,因此,参考热力学温度场中的吸热膨胀方程来推导湿度场中泥岩的吸水膨胀方程;在吸水率低于40%的条件下,定义泥岩膨胀体变随其吸水率变化的影响因数为泥岩的线膨胀系数,基于热力学理论,以泥岩的吸水率、线膨胀系数、渗透系数类比为热力学中物体的温度、热膨胀系数、导热系数对泥岩遇水膨胀产生的变形进行计算。
对于吸热膨胀,热传导过程遵循傅里叶定律[18-20],为

式中:q为热流密度,W·m-2;k为导热系数,W·m-1·K-1;为温度梯度,K·m-1;n为法向单位矢量。
以此获得热传导微分控制方程为
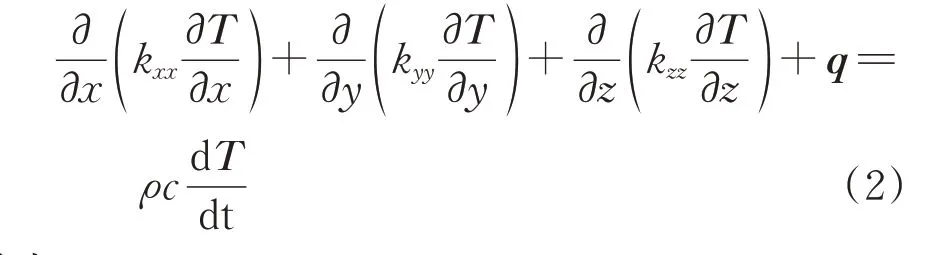
其中,
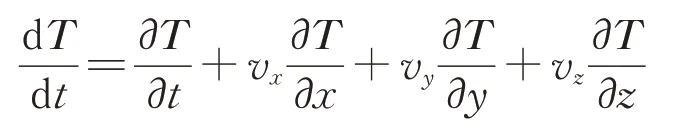
式中:vx,vy和vz分别为x,y和z方向媒介的传导速率;kxx,kyy和kzz分别为x,y和z方向的导热系数;ρ为密度,kg·m-3;c为 热 容,J·K-1;分别为x,y和z方向的温度梯度。
将微分方程转化为等效的体积积分形式,即
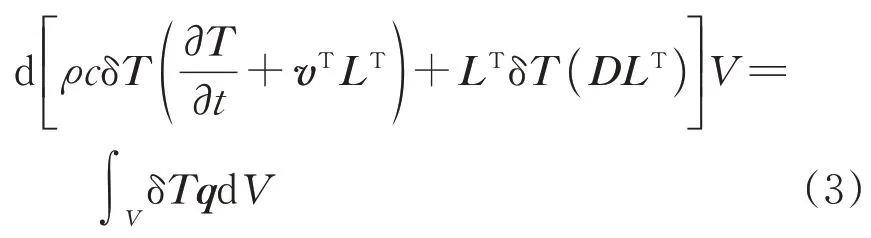
其中,

式中:v为热传导速率矩阵;dV为体积分;LT为单元体积矩阵;δT为温度的虚变量;D为材料的热传导属性矩阵。
以单元节点温度为未知数的多项式为

式中:NT为单元形函数;Te为节点温度矢量。
由式(1)—式(4)得到每个单元的温度梯度和热流密度计算式,分别为

式中:a为热梯度矢量。
将假设的温度变化代入积分方程(3),可得

其中,

式(7)即为热力学中材料在温度场下的平衡方程。
对于吸水膨胀,假设水分在泥岩中的渗透遵循达西定律,则获得水分在泥岩中的渗透流动方程为

对比式(1)与式(8)发现,水分在泥岩中的渗透流动方程与温度在材料里的热传导方程具有相同的函数形式。将温度梯度替换为水头梯度,水分渗透假设为热传导。
以节点含水率W为未知数的多项式为

式中:We为节点含水率矢量。
由式(1)—式(9)得到每个单元的含水率梯度和水流计算式分别为

式中:β为含水率梯度矢量;v水为单元体积内水的渗透速度矢量矩阵;S为岩石的材料属性矩阵。
最后类比得到湿度场下膨胀岩的变形计算积分方程为
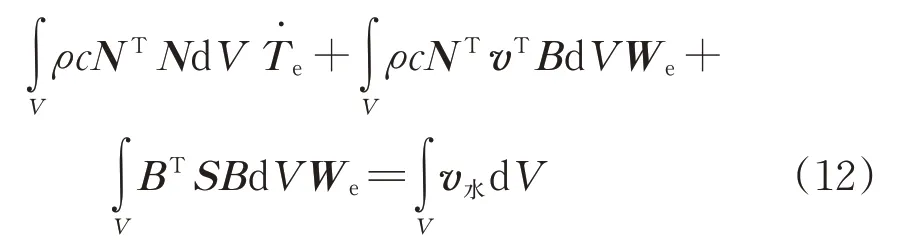
1.2 试验验证
运用有限元软件热分析模块中的稳态分析,建立热力耦合模型,对泥岩的室内侧向约束膨胀试验以及不同围压条件下的膨胀体变试验进行模拟分析。稳态分析中对温度、热膨胀系数、导热系数进行定义,根据前节的推导过程,对泥岩的吸水率、线膨胀系数、渗透系数进行确定。
对于侧向约束膨胀试验,为环刀试样限制试样模型底部所有节点竖向负方向变形及模型周围节点径向外侧变形;对于围压条件下的膨胀试验,为圆柱试样,模型边界无变形限制。计算所用参数均为试验所得,详见表4和表5。

表4 模型参数

表5 计算参数
用室内试验获得的吸水率和线膨胀系数对泥岩在该吸水率下的膨胀体变进行反算,计算结果与室内试验结果进行对比如图4 所示。从图4 可以看出:根据室内试验参数计算获得的泥岩膨胀体变与试验获得的膨胀体变十分吻合,最大误差仅为4.3%,表明这种类比热力学的分析方法能够很好地对泥岩吸水膨胀进行计算,并根据吸水率预测其膨胀发展规律。
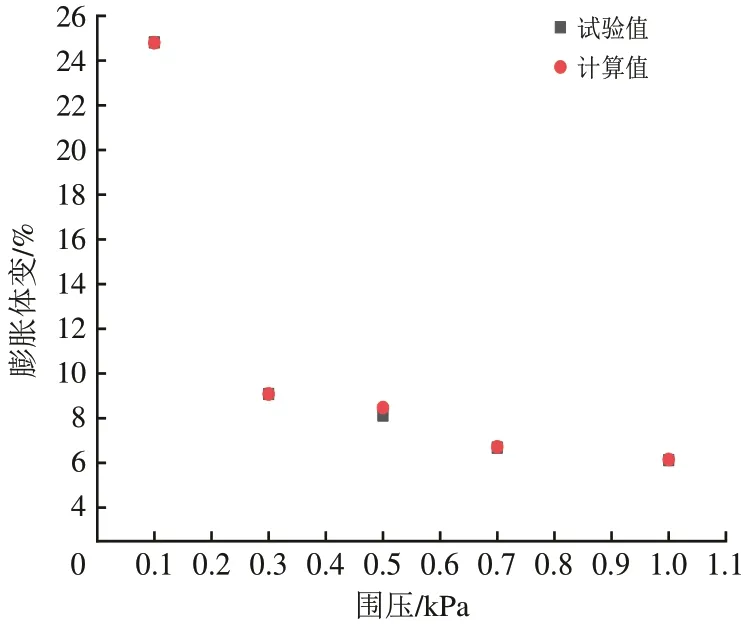
图4 计算结果与试验结果对比
因此,在实际应用中可以先进行室内膨胀试验确定泥岩吸水率、线膨胀系数、渗透系数等关键参数,再通过该方法对泥岩地基的膨胀体变进行计算,可以预测上部结构在不同吸水状态下由泥岩地基膨胀引起的变形。
2 方法应用
2.1 计算模型
以西北某高铁典型泥岩地基工点为原型,建立路基-轨道热力耦合模型。简化后路基断面形式和地基结构如图5 所示。图中:断面坡高比1∶1.75;边坡高度为10 m;横向计算长度57.7 m;纵向计算长度30 m;h为假设渗透深度。共计算分析h=3,5,7 和10 m 这4 个深度下的膨胀变形。工点处泥岩埋深浅,因此泥岩线膨胀系数采用侧向约束条件下的试验值0.187,渗透系数为1×10-10m· s-1,模型的其他材料参数[1]见表6。
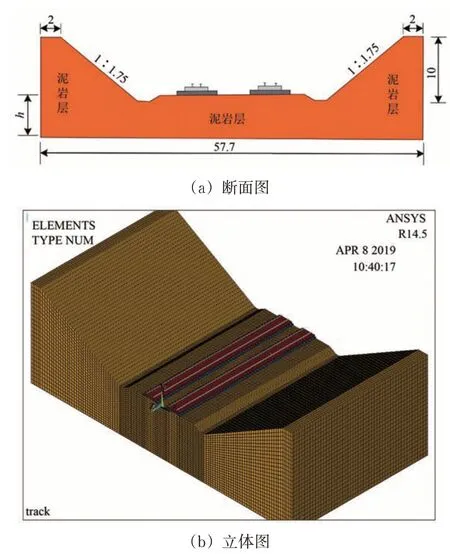
图5 几何模型(单位:m)
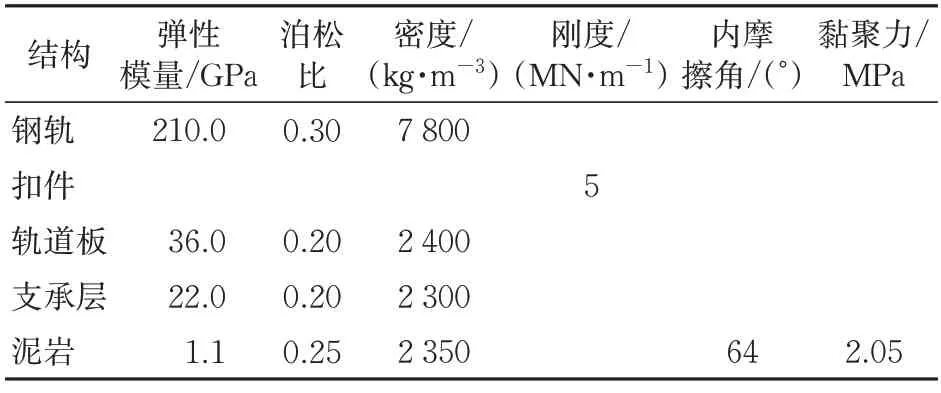
表6 模型材料参数
计算模型的边界条件如下所述。
1)位移边界条件
假定模型底面不发生变形,两侧面不发生横向变形,前后面不发生沿线路方向的纵向变形。
2)水分边界条件
水分在泥岩中的迁移渗透规律复杂,渗透系数低,在本研究提出的计算分析方法中,做以下假定。
(1)水分从边坡以及地基表面迁移渗透浸入泥岩内部,在迁移渗透过程中,泥岩表面始终保持含水率不变。
(2)不考虑泥岩膨胀的时间效应,认为计算过程中泥岩吸水充分且完全膨胀。
根据假定,定义水分边界条件为

式中:WA为泥岩地基上表面含水率,%,取值为计算工况下的不同含水率ω;WB为泥岩底面含水率,%。
计算分析路基-轨道结构在3 种水分边界条件以及4 种渗透深度下的吸水膨胀变形状态,计算工况详见表7。
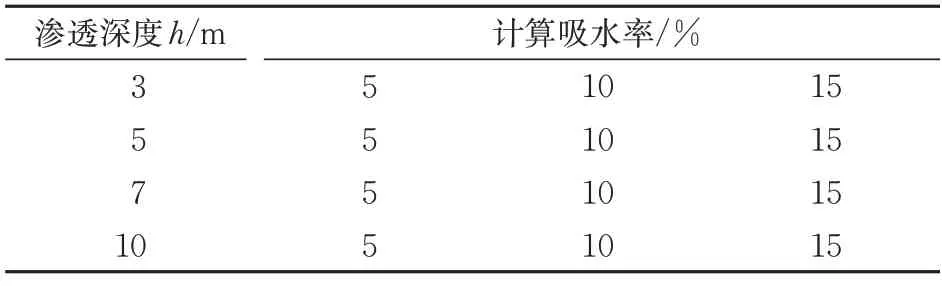
表7 计算工况
2.2 路基结构水分分布及变形状态
各计算工况下水分分布规律与变形规律基本一致,不同渗透深度和吸水率只影响地基结构的最终变形量。由于篇幅限制,仅对渗透深度10 m,吸水率10%条件下地基的水分分布状态以及变形状态进行分析,该条件下的水分分布云图以及竖向变形云图分别如图6和图7所示。

图6 地基水分分布

图7 地基竖向变形
由图6 可以看出:在空间上地基内部水分呈条带状分布且与地基表面平行,吸水率沿深度方向逐渐变小,根据本文提出的计算分析方法,这种条带状的分布规律主要由水分边界条件决定;地基中间一定深度范围内水分分布明显出现了断层,这一断层发生在支承层正下方,这说明支承层的存在影响了水分在横向上的迁移,但影响深度很浅,换言之,轨道下铺设混凝土封闭层等防水措施对阻止地基膨胀作用效果不明显,水分依旧可以通过横向迁移的方式进入地基内部引起地基膨胀。
由图7 可以看出:支承层平面以下泥岩变形与地基内的水分分布规律一致;变形沿着竖向往下逐渐变小,变形最大处为边坡顶部,这主要与水分的分布规律有关,含水量沿着深度方向呈递减的趋势,不同含水量引起的变形不同。
不同含水率地基沿深度方向变形曲线如图8 所示。由图8可以看出:不同含水率不同渗透深度下泥岩地基沿深度方向上的膨胀变形规律一致,膨胀变形与深度成对数关系;每个深度下的膨胀变形包括2 部分,一部分为渗入该层位的水分引起的膨胀,还有一部分为该层以下的膨胀变形,即图示膨胀变形为累积变形;结合地基竖向变形云图进行分析可以发现,地表含水率越高,渗透深度越深,水分引起的膨胀变形越大。

图8 不同含水率地基沿深度方向变形曲线
为了明确不同渗透深度以及含水率下泥岩地基的膨胀变形规律,绘制不同渗透深度下地基上拱变形随含水率变化曲线如图9所示。由图9可以看出:相同渗透深度下,上拱变形与含水率呈线性关系;相同含水率条件下,上拱变形与渗透深度呈线性关系;含水率越高,渗透深度对上拱变形的影响越大,同样渗透深度越大,含水率对上拱变形的影响也越大。

图9 不同渗透深度下地基上拱变形曲线
2.3 现场监测及验证
对上述典型泥岩工点,沿路基深度方向对基床表层、基床底层及地基进行垂向分层变形监测:位移计布置孔位设在距离轨道板0.5 m 的路肩上,相同监测断面沿线路纵向间距0.5 m 设置不同深度的布置孔,同时设置1 个参照孔,参照孔深度至少30 m,监测孔深度以及数量由不同断面结构特征决定,保证可以监测到每个层位。
位移计布置示意图如图10 所示。自动采集设备固定在路肩外侧,采用不锈钢槽对传感器连接线进行保护并引至路肩外侧与采集设备连接。自动采集设备通过物联网将监测信息传至终端,供监测人员对数据进行分析。

图10 位移计布置示意图(单位:m)
半年内该工点在3 个层位上沿深度方向的变形曲线如图11 所示。由图11 可以看出:半年时间内路基累计上拱了19.9 mm,平均上拱速率为3.3 mm·月-1;2018 年8 月中旬增长速率明显增大,主要原因是该地区在2018 年8 月12 日出现了强降雨,最大降雨量达32.3 mm,降雨渗透至泥岩层导致泥岩吸水膨胀,随着时间的推移,没有额外水分补充,最终膨胀速率变缓;2018 年12 月份膨胀变形速率突增,但增长速率小于该年8月份,主要原因是该地区12 月份出现强降雪,降雪融化下渗导致泥岩吸水发生了膨胀,相对于强降雨,降雪融化后的水分明显小于降雨,所以增长速率没有降雨时变化明显,影响深度为1.5 m 范围内;变形最大位置在1.5~3.5 m,变形量为14.8 mm,其次是表面以下1.5 m 范围内,变形量为4.2 mm,3.5~6.5 m 范围内变形较小,变形量为0.9 mm。由此可以明确膨胀发生层位为3.5 m,由于水分在不断地蒸发且泥岩的渗透系数低,水分未能到达6.5 m层的泥岩处。

图11 深度方向不同层位竖向变形
路基结构的上拱变形计算值与实测结果对比见表8。由表8 可以看出:渗透深度3 m、吸水率5%时,路基结构的上拱变形计算值为17 mm;渗透深度3 m,现场取样获得泥岩含水率为4%~8%条件下,监测路基上拱变形为19.9 mm;即相近条件下实测值与计算值仅差2.9 mm,这表明提出的路基上拱变形计算方法合理有效,能在实际工程中对泥岩地区的路基上拱变形进行合理的预测,为前期设计以及后期养护维修提供依据。

表8 预测结果对比
3 结论
(1)类比热力学中吸热膨胀方程提出的泥岩膨胀体变计算分析方法,充分考虑了泥岩的吸水膨胀特征,且具有误差小的优势。热传导和渗流均与各自的势函数存在线性关系,吸热膨胀与吸水膨胀则为膨胀系数与温度和湿度的线性关系,相同的函数形式以及相似的膨胀过程表明该方法在理论上合理可行;室内试验与计算结果误差最大为4.3%,变形监测结果与仿真模拟结果在合理范围内。
(2)基于考虑渗流的泥岩膨胀体变计算分析方法,能够预测膨胀岩地区高速铁路地基的膨胀变形规律,水分分布规律以及明确轨道结构的上拱变形量。水分在地基面以下呈条带状分布且平行于地基表面;泥岩地基的膨胀变形沿着深度方向逐渐变小,与深度呈对数关系;膨胀变形与地基面吸水率以及渗透深度呈线性关系。通过试验测试明确泥岩渗透系数、渗透深度以及降水情况,则可计算出该段路基上轨道结构的上拱变形。
